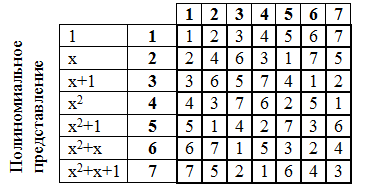Решение уравнений в полях галуа

Видео:Начала теории Галуа: разрешимость алгебраических уравнений в радикалахСкачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Раздел создан при поддержке компании

Видео:Лекция №1 — КОНЕЧНЫЕ ПОЛЯСкачать

Поля Галуа

В настоящем разделе буква $ p_ $ обозначает простое число.

Видео:Простые поля ГалуаСкачать

Структура конечного поля

Существование конечных полей, т.е. полей, состоящих из конечного числа элементов установлено в пункте ☞ ПОЛЕ.

Пример. Множество $ mathbb Z_

$ классов вычетов по простому модулю $ p_ $ образует поле относительно операций сложения и умножения.

Рассмотрим теперь конечные поля самого общего вида. Любое такое поле $ mathbb F_ $ должно содержать нейтральный элементы относительно сложения и умножения: $ mathfrak o $ — нулевой и $ mathfrak e $ — единичный. Начнем последовательно складывать единичные элементы $$ mathfrak a_1= mathfrak e, mathfrak a_2=mathfrak e+mathfrak e, mathfrak a_3=mathfrak e+mathfrak e+mathfrak e,dots $$ Поскольку, по предположению, поле содержит лишь конечное число элементов, то элементы последовательности $ _ $ должны повторяться. Если $ mathfrak a_k= mathfrak a_ $ при $ k ♦

Простое число $ M=p_ $ из предыдущей теоремы называется характеристикой конечного поля.

Теорема 2. Порядок (число элементов) любого конечного поля равен некоторой степени его характеристики: $$ operatorname (mathbb F) = p^m quad mbox quad p mbox quad m in mathbb N . $$

Доказательство. В предыдущей теореме было доказано, что конечное поле $ mathbb F $ характеристики $ p_ $ содержит $ p_ $ различных элементов: $$ mathfrak a_0=mathfrak o, mathfrak a_1,dots,mathfrak a_ quad npu quad mathfrak a_j= underbrace_ . $$ Это множество обладает всеми свойствами поля и изоморфно полю $ mathbb Z_p $. Изоморфизм устанавливается соответствием $ mathfrak a_j mapsto overline j $. Действительно, по предположению $ mathfrak a_p= mathfrak o $, но тогда $$ mathfrak a_

= mathfrak a_1, mathfrak a_

= mathfrak a_2, dots , mathfrak a_

= mathfrak a_j, dots , $$ а следовательно, $ mathfrak a_j+ mathfrak a_k=mathfrak a_=mathfrak a_< j+k pmod

> $. Таким образом $ mathfrak a_j+ mathfrak a_k mapsto overline $, т.е. соответствие сохраняет результат сложения. Результат умножения также сохраняется, поскольку на основании свойств поля (в частности, дистрибутивности умножения относительно сложения), следует $$ mathfrak a_j cdot mathfrak a_k=mathfrak a_ = mathfrak a_<jk pmod

> , $$ т.е. $ mathfrak a_j cdot mathfrak a_k mapsto overline $.

Установленный изоморфизм позволяет утверждать, что любой элемент $ mathfrak a_j ne mathfrak o $ имеет обратный среди чисел того же множества: $ mathfrak a_^ = mathfrak a_ $, где $ s_ $ — число, обратное $ j_ $ относительно умножения по модулю $ p_ $.

Если в поле $ mathbb F $ нет других элементов, то $ mathbb F = _^ $ и теорема доказана: $ operatorname (mathbb F) = p $. Предположим, что существует $ mathfrak A in mathbb F $ и $ mathfrak A notin _^ $. Тогда множество $$ _^ $$ определяет $ p^2 $ различных элементов поля $ mathbb F $. Действительно, если $$ mathfrak a_<j_>+ mathfrak a_<k_> cdot mathfrak A = mathfrak a_<j_>+ mathfrak a_<k_> cdot mathfrak A , mbox quad mathfrak a_<j_>- mathfrak a_<j_>=(mathfrak a_<k_>-mathfrak a_<k_>) mathfrak A . $$ Если $ mathfrak a_<k_>-mathfrak a_<k_> ne mathfrak o $, то, по доказанному в предыдущем абзаце, существует обратный к элементу $ mathfrak a_<k_>-mathfrak a_<k_> $ и этот элемент находится в том же множестве $ _^ $. Тогда из последнего равенства следует, что $$ mathfrak A=(mathfrak a_<k_>-mathfrak a_<k_>)^ (mathfrak a_<j_>- mathfrak a_<j_>) quad Rightarrow quad mathfrak A in _^ , $$ что противоречит предположению. Если же $ mathfrak a_<k_>- mathfrak a_<k_> = mathfrak o $, то тогда и $ mathfrak a_<j_>-mathfrak a_<j_> = mathfrak o $.

Если в поле $ mathbb F $ нет других элементов, то $ mathbb F =_^ $ и $ operatorname (mathbb F) = p^2 $. В противном случае, существует элемент $ mathfrak B_ $, не входящий в это подмножество, и мы рассмотрим множество $$ < mathfrak a_j+ mathfrak a_k cdot mathfrak A + mathfrak a_cdot mathfrak B >_^ , $$ которое определяет $ p^3 $ различных элементов поля $ mathbb F $. Дальнейший ход доказательства аналогичен предыдущим рассуждениям. Поскольку, по предположению, число элементов поля конечно, то процесс должен завершиться за конечное число шагов и если последний шаг имеет номер $ m_ $, то получим утверждение теоремы. ♦

Пример. Рассмотрим поле, состоящее из $ 4_ $-х элементов. Два из них — это нейтральные элементы $ mathfrak o $ и $ mathfrak e $. Два оставшихся обозначим $ mathfrak a $ и $ mathfrak b $. Попробуем выписать для этих элементов таблицы сложения и умножения, руководствуясь только аксиомами поля. Начнем со сложения. На основании того, что характеристика поля равна $ p=2 $ получаем $$ mathfrak e + mathfrak e = mathfrak o . $$ Чему может равняться сумма $ mathfrak a+ mathfrak e $? Если $ mathfrak a+ mathfrak e= mathfrak o $, то, прибавляя к обеим частям равенства $ mathfrak e $, на основании предыдущего равенства, получаем $ mathfrak a = mathfrak e $, что противоречит предположению, что $ mathfrak a $ отличен от $ mathfrak o $ и $ mathfrak e $. Аналогичным приемом показываем невозможность равенства $ mathfrak a+ mathfrak e= mathfrak e $ — оно приводит к $ mathfrak a = mathfrak o $. Пусть теперь $ mathfrak a+ mathfrak e= mathfrak a $. На основании аксиомы поля 3 , для элемента $ mathfrak a $ должен существовать противоположный относительно сложения; мы пока не знаем, чему он равен, но знаем, что он существует. Обозначим его $ x_ $, тогда $ mathfrak a +x = mathfrak o $. Прибавим этот элемент к обеим частям предполагаемого равенства $ mathfrak a+ mathfrak e= mathfrak a $, получим $ mathfrak e= mathfrak o $, что незаконно.

Наконец, $$ mathfrak a cdot mathfrak b = mathfrak a cdot (mathfrak a+mathfrak e) = mathfrak a cdot mathfrak a + mathfrak a = mathfrak b + mathfrak a = mathfrak e . $$ Окончательно: $$ begin mathbb & mathfrak o & mathfrak e & mathfrak a & mathfrak b \ hline mathfrak o & mathfrak o & mathfrak o & mathfrak o & mathfrak o \ mathfrak e & mathfrak o & mathfrak e & mathfrak a & mathfrak b \ mathfrak a & mathfrak o & mathfrak a & mathfrak b & mathfrak e \ mathfrak b & mathfrak o & mathfrak b & mathfrak e & mathfrak a end $$ ♦

Итак, цепочкой рассуждений мы пришли к выводу: если существует конечное поле из $ 4_ $-х элементов, то в нем операции сложения и умножения должны производиться по единственно возможным сценариям, которые описываются полученными таблицами. Однако, остался открытым вопрос:

Нет ли противоречий в этих построенных таблицах?

В самом деле, возможно, что существует не найденная нами цепочка действий, которая приведет к противоречию с каким-то результатом из полученных таблиц. Ответ на этот вопрос оказывается отрицательным: противоречий мы не получим.

Пример. Рассмотрим множество, состоящее из квадратных матрицы второго порядка

$$ mathfrak o= left( begin 0 & 0 \ 0 & 0 end right), mathfrak e= left( begin 1 & 0 \ 0 & 1 end right), mathfrak a= left( begin 1 & 1 \ 1 & 0 end right), mathfrak b= left( begin 0 & 1 \ 1 & 1 end right). $$ В этом множестве операцию сложения определим как операцию сложения матриц по модулю $ 2_ $: $$ left(begin a_& a_ \ a_&a_ end right)+ left(begin b_& b_ \ b_&b_ end right)= left(begin a_+b_ pmod & a_+b_ pmod \ a_+b_ pmod & a_+b_ pmod end right) $$ а операцию умножения — как операцию умножения матриц, но тоже по модулю $ 2_ $, т.е.: $$ left(begin a_& a_ \ a_&a_ end right)times left(begin b_& b_ \ b_&b_ end right) = left(begin a_b_ +a_b_ pmod & a_b_ +a_b_ pmod \ a_b_ +a_b_ pmod & a_b_ +a_b_ pmod end right) . $$ Можно проверить, что таблицы действий с элементами этого множества совпадают с таблицами, приведенными выше. ♦

Пример конечного поля порядка $ p^ $ будет приведен ☟ НИЖЕ. Любое такое поле называется полем Галуа и обозначается 1) $ mathbf(p^m) $.

Видео:57 Группа Галуа поля корней 12-й степени из единицыСкачать

Обобщенная теорема Ферма

Теорема. Любой элемент $ mathfrak a in mathbf(p^m) $ удовлетворяет равенству$$ mathfrak a^

— mathfrak a = mathfrak o . $$

Доказательство аналогично доказательству малой теоремы Ферма. Обозначим для краткости $ q=p^m $, и рассмотрим все ненулевые элементы поля $$ mathfrak a_1,dots, mathfrak a_ . $$ Если $ mathfrak a ne mathfrak o $, то домножим его на все эти элементы: $$ mathfrak a mathfrak a_1,dots, mathfrak a mathfrak a_ . $$ Получились снова элементы поля. Они все отличны от $ mathfrak o $ (поскольку в поле не существует делителей нуля) и все различны: $$ mathfrak a mathfrak a_j = mathfrak a mathfrak a_k quad Rightarrow quad mathfrak a (mathfrak a_j — mathfrak a_k)= mathfrak o quad Rightarrow quad mathfrak a = mathfrak o quad mbox quad mathfrak a_j = mathfrak a_k . $$ Следовательно множество $ _^ $ совпадает со множеством $ _^ $, но тогда произведения элементов этих множеств одинаковы: $$ prod_^ (mathfrak a mathfrak a_j) = prod_^ mathfrak a_j quad Rightarrow quad a^ prod_^ mathfrak a_j = prod_^ mathfrak a_j . $$ Произведение ненулевых элементов поля отлично от $ mathfrak o $, следовательно $$ mathfrak a^= mathfrak e ; $$ это равенство справедливо для любого ненулевого элемента поля. Умножив его на $ mathfrak a $, получим равенство из условия теоремы, которому будет удовлетворять и $ mathfrak a = mathfrak o $. ♦

Теорема. Любой элемент $ mathfrak a in mathbf(p^m) $ удовлетворяет равенству

Будем называть выражение вида $$ mathfrak x^m + A_1 mathfrak x^ + dots + A_ = mathfrak o $$ при $ subset < mathfrak a_0=mathfrak o, mathfrak a_1,dots,mathfrak a_> $ алгебраическим уравнением в $ mathbf(p^m) $ степени $ m_ $ относительно неизвестной $ mathfrak x_ $.

Доказательство. При доказательстве теоремы 2 из предыдущего пункта было показано, что в любом поле $ mathbb P $ найдутся $ m_ $ элементов $ mathfrak A_1=mathfrak e, mathfrak A_2,dots, mathfrak A_m $ таких, что любой элемент поля можно выразить в виде их линейной комбинации с коэффициентами из множества $ < mathfrak a_>_^ $. Выразим в виде таких линейных комбинаций элементы $ mathfrak a, mathfrak a mathfrak A_1, mathfrak a mathfrak A_2,dots, mathfrak a mathfrak A_m $: $$ begin mathfrak a &=& A_ +A_ mathfrak A_2+dots+ A_ mathfrak A_m, \ mathfrak a mathfrak A_2 &=& A_ +A_ mathfrak A_2+dots+ A_ mathfrak A_m, \ dots & & dots \ mathfrak a mathfrak A_m &=& A_ +A_ mathfrak A_2+dots+ A_ mathfrak A_m, end qquad npu quad < A_>_^m subset < mathfrak a_>_^ . $$ Перепишем эти уравнения: $$ begin (A_- mathfrak a) & +A_ mathfrak A_2 & +dots & + A_ mathfrak A_m &=& mathfrak o, \ A_ & +(A_- mathfrak a) mathfrak A_2 &+dots & + A_ mathfrak A_m &=& mathfrak o, \ dots & & & & & dots \ A_ & + A_ mathfrak A_2 & +dots+ & (A_- mathfrak a) mathfrak A_m &=& mathfrak o. end $$ Эта система уравнений, рассматриваемая относительно элементов поля $ mathfrak A_1=mathfrak e, mathfrak A_2,dots, mathfrak A_m $ является линейной и однородной.

Поскольку эта однородная система имеет нетривиальное решение ( $ mathfrak A_1=mathfrak ene mathfrak o $), ее определитель должнен быть равен нулевому элементу поля: $$ left|begin A_- mathfrak a & A_ & dots & A_ \ A_ & A_- mathfrak a& dots & A_ \ dots & & & dots \ A_ & A_& dots & A_- mathfrak a end right|= mathfrak o . $$ Определитель в левой части является полиномом от $ mathfrak a $ степени $ m_ $ с коэффициентами, которые полиномиально же зависят от величин $ < A_>_^m $, т.е., в конечном итоге, от величин $ < mathfrak a_>_^ $. ♦

Резюмируем: элемент $ mathfrak a $ поля $ mathbf(p^m) $ должен удовлетворять одновременно двум алгебраическим уравнениям в этом поле: $ mathfrak x^

— mathfrak x = mathfrak o $ и некоторому уравнению $ mathfrak x^m + A_1 mathfrak x^ + dots + A_ = mathfrak o $ степени $ m_ $. Если бы мы имели дело с обычными алгебраическими уравнениями одной переменной с целыми коэффициентами, то мы могли бы сделать заключение о существовании зависимости между коэффициентами этих уравнений в виде некоторого алгебраического равенства (см. ☞ РЕЗУЛЬТАНТ ). В случае же конечного поля, можно вывести более глубокое заключение: второй полином оказывается делителем первого. Осталось только ввести операцию деления полиномов в конечном поле, к чему мы и приступаем.

Видео:Что сделал Галуа?Скачать

Пример конечного поля

Полином $ F_(x) $ с целыми коэффициентами называется неприводимым по модулю p если его нельзя представить в виде $$ F(x)equiv F_1(x)F_2(x)+ p G(x) , $$ где $ F_1, F_2,G $ — полиномы с целыми коэффициентами и $ deg F_1 ♦

Пример. Приводим ли полином $ 2,x^2+2,x-1 $ по модулю $ 5_ $?

Решение. Рассмотрим всевозможные комбинации потенциально возможных линейных множителей с коэффициентами из множества $ $: $$ 2,xpm 1, 2,xpm 2, xpm 2, xpm 1 . $$ Ни одна пара при перемножении не дает требуемый полином.

Ответ. Нет.

Рассмотрим полином $ f_(x) $ степени $ n_ge 1 $ с целыми коэффициентами и нормализованный (т.е. со старшим коэффициентом равным $ 1_ $): $$ f(x)=x^n+a_1x^+dots+a_n in mathbb Z[x] . $$ Доказать, что частное и остаток от деления произвольного полинома $ g_ (x)in mathbb Z[x] $ на $ f_(x) $ будут полиномами с целыми коэффициентами.

Подсказка: см. доказательство теоремы ☞ ЗДЕСЬ.

Полиномы $ subset mathbb Z[x] $ называются сравнимыми по двойному модулю $ p, f(x) $ если их разность может быть представлена в виде $$ F_1(x)-F_2(x) equiv pcdot G(x) + f(x) H(x) quad npu quad subset mathbb Z[x] . $$ Иными словами, остаток от деления $ F_1(x)-F_2(x) $ на $ f_(x) $ представляет собой полином, все коэффициенты которого кратны $ p_ $: $$ left( F_1(x)-F_2(x) pmod right) pmod

equiv 0 ; $$ здесь знак $ equiv_ $ обозначает тождественное равенство. В [1] для этого понятия используется обозначение $$ F_1(x)equiv F_2(x) quad (operatorname p,f(x)) , $$ на мой взгяд, очень наглядное. Однако ни в каком другом источнике я его не встречал.

Пример. Найти все значения параметра $ alpha in mathbb Z $, при которых полиномы

$$ F_1(x)=7,x^3+4,x^2-x-3 quad u quad F_2(x)=3,x^3-5,x^2+alpha, x+7 $$ будут сравнимы по модулю $ 5,, x^2+x+2 $.

Решение. Делим $ F_1(x)-F_2(x) $ на $ x^2+x+2 $: $$ F_1(x)-F_2(x) equiv (4,x+5)(x^2+x+2)+[(-14-alpha),x-20] . $$ Остаток от деления равен $ (-14-alpha),x-20 $, по модулю $ 5_ $ он сравним с $ (1-alpha), x $. Коэффициент при $ x_ $ делится на $ 5_ $ только при условии

Ответ. $ alpha equiv 1 pmod 5 $.

Будем использовать обозначение $$ F(x)= F_1(x) quad (operatorname p,f(x)) $$ в том же смысле, что в разделе ☞ МОДУЛЯРНАЯ АРИФМЕТИКА использовалось обозначение $ x = A pmod $, т.е. полиному $ F_(x) $ присваивается значение остатка от деления $ F_1(x) $ на $ f_(x) $, в котором дополнительно производится усечение каждого коэффициента до его остатка от деления на $ p_ $.

Пример. Для

$$ F_1(x)=5,x^4-x^2+x-4, f(x)= x^3+2,x^2+3,x-6 $$ и $ p=7 $ имеем $$ F_1(x)equiv (5,x-10)f(x) +4,x^2+61,x-64 quad Rightarrow quad F(x)=4,x^2+5,x+6 equiv F_1(x) quad (operatorname 7,f(x)) . $$

Теорема. Пусть $ f_(x) $ — нормализованный неприводимый по модулю $ p_ $ полином степени $ mge 1 $. Множество полиномов

$$ mathbb P_

= < F (x)=A_0+A_1x+dots+A_x^ mid <A_0,A_1,dots,A_> subset > , $$ рассматриваемое относительно операции сложения по модулю $ p_ $: $$ F_1(x)+F_2(x) pmod

$$ и операции умножения по двойному модулю $ p, f(x) $: $$ F_1(x) F_2(x) quad (operatorname p,f(x)) $$ образует поле Галуа $ mathbf(p^m) $.

Доказательство. Все элементы множества $ mathbb P_

$ различны, поскольку каждый определяется набором своих коэффициентов $ (A_0,A_1,dots,A_) $ однозначно. Каждый из коэффициентов, независимо от других, может принимать $ p_ $ различных значений, следовательно $ operatorname ( mathbb P_

) = p^m $.

Введенные во множестве $ mathbb P_

$ операции удовлетворяют аксиомам 1 — 8 поля; сложность вызовет лишь проверка аксиомы 8 о существовании полинома, обратного произвольному полиному $ F(x) in mathbb P_

, F(x) notequiv 0 $ относительно умножения по двойному модулю $ p,f(x) $. Требуется удостовериться, что существует полином $ U(x) in mathbb P_

$ такой, что $$ U(x)F(x) quad (operatorname p,f(x)) equiv 1 . $$

Если $ F_(x) $ тождественно равен константе $ F(x)equiv A_0 $, то искомый полином $ U(x) $ тоже будет константой: $ U(x)equiv U_0 $, где $ U_0A_0 equiv 1 pmod

$. Последнее сравнение имеет решение для любого $ A_0in $, это решение будет единственны в том же множестве, и оно называется мультипликативным обратным числу $ A_0 $ по модулю $ p_ $. Соответствующую теорию и сопутствующие алгоритмы нахождения см. ☞ ЗДЕСЬ; сугубо же для теоретических манипуляций нам достаточно будет его представления посредством малой теоремы Ферма: $$ A_0^= A^ pmod

. $$

Предположим теперь, что $ F(x) notequiv const $: $$ F(x) = A_0+A_1x+dots+A_x^ quad npu quad A_ ne 0, ell > 0 . $$

Разделим полином $ f_(x) $ на $ F(x) $: $$f(x)equiv q_1(x)F(x)+r_1(x) , $$ здесь $ deg q_1 = m-ell, deg r_1 0 $. Разделим целочисленный полином $ F_(x) $ на целочисленный полином $ R_1(x) $: $$ F(x) equiv q_2(x) R_1(x) + r_2(x) , quad deg r_2 3) $$ F(x)equiv Q_2(x) R_1(x) quad Rightarrow quad f(x)equiv Q_1(x)F(x)+R_1(x) equiv R_1(x) (Q_1(x)Q_2(x)+1) , $$ откуда вытекает приводимость полинома $ f_(x) $ по модулю $ p_ $. Домножаем тождество $$ F(x)equiv Q_2(x) R_1(x) + D_0 $$ на мультипликативное обратное числу $ D_0 $ по модулю $ p_ $, представив его, например, в виде $ D_0^ pmod

$. Получим $$ D_0^ F(x) — D_0^Q_2(x)R_1(x) equiv 1 pmod

. $$ Подставим в это тождество представление для $ R_1(x) $ из его определения в предыдущем абзаце: $$ R_1(x) equiv f(x)- Q_1(x)F(x), $$ приходим к тождеству $$D_0^ (Q_1(x)Q_2(x)+1)F(x)-D_0^Q_2(x)f(x) equiv 1 . $$ Из него следует, что в качестве полинома $ U(x) $, удовлетворяющего $$ U(x)F(x) quad (operatorname p,f(x)) equiv 1 , $$ можно взять $ D_0^ (Q_1(x)Q_2(x)+1) pmod

$.

Наконец, если полином $ R_2(x) $ не является константой: $ deg R_2>0 $, то разделим целочисленный полином $ R_1(x) $ на целочисленный полином $ R_2(x) $: $$ R_1(x) equiv q_3(x) R_2(x) + r_3(x) , quad deg r_3 ♦

Практическое нахождение элемента, обратного в поле Галуа заданному, возможно разными способами. Все они, прямо или опосредовано, завязаны на полиномиальное тождество, известное под названием тождества Безу: это тождество имеет вид $$ v(x)f(x)+u(x)g(x)equiv 1 . $$ При фиксированных полиномах $ f_(x) $ и $ g_(x) $ его выполнимость (хотя бы при одной паре полиномов $ u(x) $ и $ v(x) $) имеет место тогда и только тогда, когда $ f_(x) $ и $ g_(x) $ взаимно просты: $ operatorname(f,g) equiv 1 $. Способы решения этого тождества в бесконечных полях посредством вычисления континуанты изложены в ☞ ПУНКТЕ; менее практичен, но более нагляден способ, основанный на представлении результанта полиномов $ f_(x) $ и $ g_(x) $ в виде подходящего определителя, составленного из коэффициентов этих полиномов: см. ☞ ЗДЕСЬ. Можно воспользоваться любым из этих способов для получения промежуточного результата в задаче обращения элемента в поле Галуа: для полиномов $ f_(x) $ и $ F_(x) $ с целочисленными коэффициентами, сначала получить представления полиномов $ v(x) $ и $ u(x) $ с коэффициентами рациональными, а затем избавиться от знаменателей дробей переходом к обратным по модулю $ p_ $. Проиллюстрируем эту идею на примере.

Пример. В поле $ mathbf(7^5) $, порожденном полиномов $ f(x)=x^5+3,x+1 $, найти элемент обратный $ 2,x^4+3,x^3+4,x+1 $.

Решение. Тождество Безу $$ v(x)f(x)+u(x)F(x)equiv 1 . $$ будет иметь место при 4) $$ u(x)=-frac-fracx-fracx^2+fracx^3-fracx^4, quad v(x)equiv dots $$ Далее, решаем сравнения $$ 650,z_1 equiv 1, 1300 ,z_2 equiv 1, 325 , z_3 equiv 1 pmod $$ получаем мультипликативные обратные к знаменателям $ z_1=6,z_2=3,z_3=5 pmod $. Избавляемся от знаменателей в коэффициентах полинома $ u_(x) $: $$U(x)=-1561 cdot 6-33cdot 3,x -22cdot 5,x^2+307cdot 3,x^3-1023 cdot 3,x^4 equiv_ dots $$

Ответ. $ (2,x^4+3,x^3+4,x+1)^ quad (operatorname 7,x^5+3,x+1) = 4,x^4+4,x^3+2,x^2+6,x $.

Пример. Построить поле $ mathbf(4) $.

Решение. Здесь $ p=2 $ и $ m_=2 $. Полином $ f(x)=x^2+x+1 $ является неприводимым по модулю $ 2_ $. Согласно теореме, множество из четырех полиномов $ $ с операцией сложения по модулю $ 2_ $ и операцией умножения по двойному модулю $ 2, x^2+x+1 $ образует поле. Результаты операций, собранные в таблицы $$ begin mathbb & 0 & 1 & x & x+1 \ hline 0 & 0 & 1 & x & x+1 \ 1 & 1 & 0 & x+1 & x \ x & x & x+1 & 0 & 1 \ x+1 & x+1 & x & 1 & 0 end qquad qquad begin mathbb & 0 & 1 & x & x+1 \ hline 0 & 0 & 0 & 0 & 0 \ 1 & 0 & 1 & x & x+1 \ x & 0 & x & x+1 & 1 \ x+1 & 0 & x+1 & 1 & x end $$ полностью соответствуют приведенным в начале раздела, где выводились правила действий в произвольном поле $ mathbf(4) $. Иными словами, существует изоморфизм между произвольным полем $ mathbf(4) $ (например полем из четырех матриц, построенным в конце ☞ ПУНКТА ) и полем из полиномов, построенным в настоящем примере. ♦

Теорема. Конечные поля одинакового порядка изоморфны, т.е. между элементами этих полей можно установить такое взаимно-однозначное соответствие, которое сохраняет результаты сложения и умножения элементов.

Доказательства этой теоремы, приведенные в литературе, оказались трудны для моего понимания, поэтому я просто привожу проверку этого утверждения на примере ☞ ЗДЕСЬ.

Видео:Канунников А. Л. - Начала теории Галуа - Критерий разрешимости уравнений в радикалахСкачать

Полиномы, неприводимые по модулю

В настоящем пункте под неприводимым полиномом понимается нормализованный неприводимый полином.

Теорема 1. Любой неприводимый по модулю $ p_ $ полином степени $ n_ $ является делителем полинома $ x^

— x $ (по модулю $ p_ $).

Доказательство. В предыдущем пункте было доказано, что если $ f_(x) $ неприводимый по модулю $ p_ $ полином степени $ n_ $, то множество $ mathbb P_

$ полиномов степеней $ ♦

Таким образом, чтобы найти все неприводимые по модулю $ p_ $ полиномы степени $ n_ $ следует разложить полином $ x^

— x $ на неприводимые по модулю $ p_ $ множители. При этом часть множителей может иметь степень $ ☞ ЗДЕСЬ.

Теорема 3. Полином $ x^

— x $ разлагается по модулю $ p_ $ на неприводимые полиномы, степени которых равны или $ m_ $ или делителям $ m_ $.

Непосредственным следствием теоремы 2 является

Теорема 4. Обозначим через 6) $ xi_p (k) $ число неприводимых по модулю $ p_ $ полиномов степени $ k_ $. Имеет место равенство

$$ p^m=sum_ k xi_p (k) ; $$ здесь суммирование производится по всем индексам $ k_ $ , являющимися делителями числа $ m_ $.

Определить $ xi_p (m) $ для случая простого $ m_ $. Установить для этого случая асимптотику $ xi_p (m)/p^m $ при $ m to infty $.

Если в каноническом разложении числа $ m_ $ на множители содержатся только различные простые числа, то имеет место равенство:

$$ xi_p (m) =frac left(p^m- sum_ p^<m/k_>+sum_<k_,k_> p^<m/(k_k_)>- sum_<k_,k_,k_> p^<m/(k_k_k_)> + dots right) , $$ где $ k_1,k_2,k_3,dots $ пробегают всевозможные делители числа $ m_ $.

Пример. Определить $ xi_p (30) $.

Решение. Поскольку $ 30=2cdot 3 cdot 5 $, то имеем: $$ xi_p (30) = frac left(p^-p^-p^-p^6+p^5+p^3+p^2-p right) . $$ Так, $ xi_2 (30)= 35790267, xi_3 (30) =6863037256208 $. ♦

В поле Галуа первообразным корнем степени n из единицы называется элемент $ mathfrak a $, который удовлетворяет условиям $$ mathfrak a^n=mathfrak e , mathfrak a^k ne mathfrak e quad npu quad kin . $$ Будем также говорить, что $ mathfrak a $ принадлежит показателю n или, что $ mathfrak a $ имеет порядок n.

Теорема 5. В поле Галуа $ mathbf (p^m) $ существуют первообразные корни степени $ p^m-1 $ из единицы.

Доказательство (и критерий, часто позволяющий быстро отыскать такие корни) ☞ ЗДЕСЬ.

В поле $ mathbf (p^m) $ первообразный корень степени $ p^m-1 $ из единицы называется примитивным элементом поля.

Количество примитивных элементов поля $ mathbf (p^m) $ равно $ phi(p^m-1) $, где $ phi $ — функция Эйлера.

В любом поле Галуа группа относительно умножения — циклическая, иными словами: все ненулевые элементы поля $ mathbf (p^m) $ находятся во множестве $ < mathfrak A^0,mathfrak A^1,dots,mathfrak A^

> $ при выборе в качестве $ mathfrak A $ произвольного примитивного элемента.

Пример 1. Пусть $ p=3, m=2 $. Выбрав в качестве неприводимого по модулю $ 3_ $ полинома 7)

$$ f(x)=x^2-x-1 , ,$$ получим, что элементами поля $ mathbf (3^2) $ должны быть полиномы степени не выше $ 1_ $ с коэффициентами из множества $ $. Возьмем в качестве примитивного элемента поля полином тождественно равный 8) $ x_ $. Получим, последовательным возведением его в степень: $$ x^0equiv 1, x^1equiv x, x^2 equiv x+1 quad (operatorname 3,x^2-x-1 ) , x^3equiv xcdot x^2 equiv x^2+xequiv 2,x+1 equiv — x+1 , $$ т.е. каждый раз умножаем результат предыдущего шага на $ x_ $ и в правой части производим формальную замену $ x^2 to x+1 $; $$ begin x^4equiv -x^2+x equiv -x-1+xequiv -1,\ x^5 equiv -x,\ x^6 equiv -x^2 equiv -x-1,\ x^7 equiv -x^2-xequiv -x-1-x equiv x-1, \ x^8 equiv x^2-x equiv 1 . end $$ Цикл завершен. ♦

Теорема 6. Полином $ x^

— x $ содержит неприводимые по модулю $ p_ $ сомножители степени $ m_ $.

Доказательство. Если бы первообразный корень $ mathfrak a $ степени $ p^m -1 $ из единицы удовлетворял бы уравнению степени $ n ♦

Пример 2. Разложить полином $ x^-x $ на неприводимые по модулю $ 2_ $ множители.

Решение. Воспользуемся результатом из пункта УРАВНЕНИЕ ДЕЛЕНИЯ КРУГА. $$ x^-x equiv x left(x^-1 right) equiv x, X_1(x)X_3(x)X_5(x)X_(x) equiv $$ $$ equiv x(x-1)(x^2+x+1)(x^4+x^3+x^2+x+1)(x^8-x^7+x^5-x^4+x^3-x+1) . $$ Здесь полиномы $ X_j(x) $ — неприводимы в $ mathbb Z_ $. Чтобы найти разложение на неприводимые по модулю $ 2_ $ полиномы, воспользуемся сначала результатом теоремы 3 для определения количества этих неприводимых полиномов. Имеем: $$ begin 16 & = & 4 xi (4) & + 2xi (2) & + xi (1), \ 4 & = & & 2xi (2) & + xi (1), \ 2 & = & & & xi (1), end $$ откуда: $ xi (1)=2, xi (2)=1, xi (4)=3 $. Таким образом, получаем что по модулю $ 2_ $ имеется (в-точности) $ 2_ $ неприводимых линейных полинома, оба уже наблюдаются в разложении: $$ x quad mbox quad x-1 equiv x+1 pmod ; $$ Неприводимый полином $ 2_ $-й степени единствен — и он также уже содержится в разложении: $$ x^2+x+1 . $$ Что касается неприводимых полиномов $ 4_ $-й степени, то их должно быть $ 3_ $. Один из них уже содержится в разложении: $$ x^4+x^3+x^2+x+1 ; $$ два остальных содержатся в разложении $ x^8-x^7+x^5-x^4+x^3-x+1 $ на множители по модулю $ 2_ $: $$ x^8-x^7+x^5-x^4+x^3-x+1 equiv (x^4+x^3+1)(x^4+x+1) pmod . $$ ♦

Пример 3. Найти все неприводимые по модулю $ 2_ $ полиномы $ 3_ $-й степени.

Решение. Для получения этих полиномов — в соответствии с теоремой 3 — надо разложить на множители полином $ x^-x $. Имеем $$ x^-xequiv x(x-1)(x^6+x^5+x^4+x^3+x^2+x+1) equiv x(x-1)(x^3+x^2+1)(x^3+x+1) pmod 2 . $$ Оба полученных полинома $ 3_ $-й степени неприводимы по модулю $ 2_ $, поскольку по теореме 3 получаем $$ begin 4 & = & 3xi (3) & + xi (1), \ 2 & = & & xi (1), end $$ откуда $ xi (3)=2 $. ♦

Пример 4. Разложить полином $ x^-x $ на неприводимые по модулю $ 3_ $ множители.

Видео:Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать

Полиномы над GF(2)

Наибольшую важность для приложений в теории кодирования имеют поля $ mathbf(2^m) $. Рассмотрим примеры полей из полиномов с коэффициентами из множества $ $ — о таких полиномах часто говорят как о полиномах над GF(2). На этих примерах мы проиллюстрируем еще раз результаты предыдущих пунктов.

Заметим, что любой (не тождественно нулевой) полином из такого поля всегда нормализован.

Доказать, что любой неприводимый по модулю $ 2_ $ полином степени $ n> 1 $ имеет нечетное число мономов.

Пример. Исследовать поле $ mathbf(16) $.

Решение. Поле содержит $ 16_ $ элементов: полиномов вида $ A_0x^3+A_1x^2+A_2x+A_3 $ при $ in $. Теперь надо определить операцию умножения. Разложение полинома $ x^-x $ на неприводимые по модулю $ 2_ $ множители приведено в предыдущем пункте: $$ x^-x equiv_<_> x(x-1)(x^2+x+1)(x^4+x^3+x^2+x+1)(x^4+x^3+1)(x^4+x+1) . $$ При любом выборе неприводимого полинома $ f_(x) $ степени $ 4_ $ из трех, участвующих в этом разложении, операция умножения по двойному модулю $ 2,f(x) $ будет удовлетворять аксиомам поля. Проверим это для выбора $ f_(x)=x^4+x+1 $. Следующая таблица выражает все полиномы из поля через посредство выражений для степеней $ <x^quad (operatorname 2,f(x)) >_^ $: $$ begin x^0 & & & & 1 & 0001 & \ x^1 & & & x & & 0010 & Pi \ x^2 & & x^2 & & & 0100 & Pi \ x^3 & x^3 & & & & 1000 & \ hline x^4 & & & x & +1 & 0011 & Pi \ x^5 & & x^2 & +x & & 0110 & \ x^6 & x^3 & +x^2 & & & 1100 & \ x^7 & x^3 & & + x & +1 & 1011 & Pi \ hline x^8 & & x^2 & & +1 & 0101 & Pi \ x^9 & x^3 & & +x & & 1010 \ x^ & & x^2 &+x & +1 & 0111 \ x^ & x^3 & +x^2 & +x & & 1110 & Pi \ hline x^ & x^3 & +x^2 & + x& +1 & 1111 \ x^ & x^3 & +x^2 & & +1 & 1101 & Pi \ x^ & x^3 & & & +1 & 1001 & Pi end $$ (и если бы мы продолжили эту таблицу, то следующим шагом вышли бы на цикл: $ x^ quad (operatorname 2,f(x)) equiv 1 $). В третьем столбце стоят двоичные наборы коэффициентов полиномов, рассматриваемых в разложении по убывающим степеням $ x_ $. В четвертом столбце отмечены примитивные элементы поля, т.е. элементы, степени которых порождают все ненулевые элементы поля (одним из них являлся полином, тождественно равный $ x_ $, по которому, собственно, и составлена таблица; с тем же успехом мы могли бы рассматривать и $ <left(x^2right)^k quad (operatorname 2,f(x)) >_^ $ или $ <left(x^right)^k quad (operatorname 2,f(x)) >_^ $, и т.п.). Количество примитивных элементов равно $ phi(2^4-1)=phi(15)=8 $. Все они обязаны удовлетворять алгебраическим уравнениям, степеней равных делителям числа $ 16_ $. Все эти уравнения можно получить из разложения полинома $ x^ — x $ на неприводимые по модулю $ 2_ $ множители. Проверим это. Чтобы избежать путаницы, будем рассматривать неприводимые полиномы относительно переменной $ mathfrak x $. Проверяем, что полиномы $ x, x^2,x^4,x^8 $ удовлетворяют уравнению $ mathfrak x^4+mathfrak x+mathfrak e= mathfrak o $; везде ниже сравнения вычисляются по двойному модулю $ 2,x^4+x+1 $: $$x^4+x+1 equiv 0, (x^2)^4+(x^2)+1 equiv x^8+x^2+1 equiv x^2+1+x^2+1 equiv 0, $$ $$ begin (x^4)^4+(x^4)+1 & equiv &(x+1)^4+(x+1)+1 equiv x+(x+1)+1 equiv 0 , \ (x^8)^4+(x^8)+1 & equiv & (x^+1)^4+(x^2+1)+1 equiv x^2+(x^2+1)+1 equiv 0 . end $$ Оставшиеся $ 4_ $ примитивных элемента поля, именно, $ x^7,x^,x^,x^ $ должны удовлетворять другому уравнению $ 4_ $-й степени, которое соответствует одному из оставшихся неприводимых полиномов этой степени. В самом деле, они удовлетворяют уравнению $ mathfrak x^4+mathfrak x^3+mathfrak e= mathfrak o $: $$ (x^7)^4 + (x^7)^3+1 equiv x^+x^+1 equiv x^+x^+1equiv x^3+x^2+1+(x^3+x^2)+1 equiv 0 . $$ Последние вычисления проводились с учетом $ x^ equiv 1 $ и с использованием построенной выше таблицы для степеней $ x^ $.

Примитивные элементы поля, т.е. элементы порядка $ 15_ $, исчерпаны. Все остальные элементы поля имеют порядки, равные $ 1_, 3_ $ или $ 5_ $, т.е. — в соответствии с теоремой предыдущего пункта — делителям числа $ 15_ $. Рассмотрим последовательность $ <left(x^3right)^k quad (operatorname 2,f(x)) >_^ $: $$ (x^3)^0 equiv 1, (x^3)^1 equiv x^3, (x^3)^2 equiv x^6 equiv x^3 +x^2, (x^3)^3 equiv x^9 equiv x^3 +x, (x^3)^4 equiv x^ equiv x^3 +x^2+x+1, (x^3)^5 equiv x^ equiv 1 . $$ Итак, элемент поля $ x^ $ принадлежит показателю $ 5_ $, этому же показателю принадлежат и его степени, т.е. полиномы $ x^3 +x^2, x^3 +x, x^3 +x^2+x+1 $. Все эти полиномы удовлетворяют уравнению $ mathfrak x^4+mathfrak x^3+mathfrak x^2+mathfrak x+mathfrak e= mathfrak o $, соответствующему третьему неприводимому полиному $ 4_ $-й степени из разложения $ x^-x $. На всякий случай, осуществим выборочную проверку: $$ (x^9)^4+(x^9)^3+(x^9)^2+x^9+1 equiv x^+x^+x^3+x^9+1 equiv (x^3+x^2)+(x^3+x^2+x+1)+x^3+(x^3+x)+1 equiv 0 . $$ Теперь рассмотрим оставшиеся элементы поля: $ x^5 $ и $ x^ $. Они должны принадлежать показателю $ 3_ $, что и немедленно проверяется. Кроме того, они должны удовлетворять неприводимому уравнению из разложения $ x^-x $. Выбор однозначен — единственным кандидатом является уравнение $ 2_ $-й степени $ mathfrak x^2+ mathfrak x + mathfrak e = mathfrak o $: $$ (x^5)^2+x^5+1 equiv x^2+x+1 + (x^2+x)+1 equiv 0 . $$ Наконец, нейтральные элементы поля $ 0_ $ и $ 1_ $ — с ними все просто. ♦

Вывод. Поле Галуа одновременно обладает свойствами циклической группы, линейного пространства и алгебраического уравнения с целыми коэффициентами. С одной стороны, все ненулевые элементы поля можно представить как степени одного единственного. С другой стороны, операция сложения полиномов эквивалентна сложению векторов, составленных из их коэффициентов. Заметим, что в линейном пространстве не вводится аналога умножения векторов — такого, чтобы при умножении двух векторов получался снова вектор. С третьей стороны, все элементы поля разбиваются на подмножества, каждому из которых соответствует неприводимое алгебраическое уравнение — говорят, что элементы поля являются корнями неприводимых над GF(2) полиномов.

Для предыдущего примера составить аналоги таблицы степеней $ <mathfrak a^quad (operatorname 2,f(x)) >_^ $ при выборе в качестве $ f_(x) $
а) $ x^4+x^3+1 $; б) $ x^4+x^3+x^2+x+1 $; а также подходящего примитивного элемента $ mathfrak a $.

Решение ☞ ЗДЕСЬ.

Теперь займемся неприводимыми полиномами. Сначала оценим их число — в абсолютном количестве, а также в отношении к общему количеству полиномов степени $ k_ $: $$ begin k & 1& 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 12 & 21 & 25 & 30 \ hline xi(k) & 2 & 1 & 2 & 3 & 6 & 9 & 18 & 30 & 56 & 99 & 335 & 99858 & 1342176 & 35790268 \ hline xi(k)/2^k & 1 & 0.25 & 0.25 & 0.19 & 0.19 & 0.14 & 0.14 & 0.12 & 0.11 & 0.10 & 0.08 & 0.05 & 0.04 & 0.03 end $$

Разложить полином $ x^-x $ на неприводимые по модулю $ 2_ $ множители.

Решение ☞ ЗДЕСЬ.

Видео:ГАЛУА. Революционер в математике!Скачать

Полиномы над GF(p)

Теперь обобщим результаты разобранных в предыдущем пункте примеров. Будем рассматривать полиномы $ F_(x) $ над $ mathbf(p) $. Нас будут интересовать решения уравнения $$ F(mathfrak x) equiv mathfrak o . $$ среди элементов конечного поля $ mathbf(p^m) $. Любой такой элемент $ mathfrak a $ будем называть корнем полинома $ F_ $ в поле $ mathbf(p^m) $.

Теорема 1. Пусть $ F_(x) $ — неприводимый по модулю $ p_ $ полином степени $ n_ $ и $ mathfrak a in mathbf(p^m) $ — его корень. Тогда множество корней $ F_(x) $ в поле $ mathbf(p^m) $ совпадает с $$ mathfrak a, mathfrak a^p, mathfrak a^

,dots, mathfrak a^<p^> . $$

Доказательство. Воспользуемся теоремой Шёнеманна: для произвольного полинома $ F(x)in mathbb Z[x] $ выполняется $$ left[F(x)right]^p equiv F(x^p) pmod

. $$ Тогда если $ F(mathfrak a)= mathfrak o $, то и $ F(mathfrak a^p)= mathfrak o $, но тогда и $ F((mathfrak a^p)^p)= mathfrak o $, и т.д. С другой стороны, все элементы множества $ < mathfrak a^

>_^ $ различны. Действительно, если бы выполнялось равенство $$ mathfrak a^

=mathfrak a^

qquad npu qquad 0le j ☞ ПУНКТА. Однако равенство $$ mathfrak a^<p^>= mathfrak a $$ невозможно, поскольку $ n+j-k ☞ ПУНКТА, полином $ x^<p^>-x $ делится лишь на такие неприводимые по модулю $ p_ $ полиномы, степени которых являются делителями числа $ n+j-k $ и, следовательно, не может делиться на $ F_(x) $. ♦

Теорема 2. Все корни неприводимого полинома $ F_(x) $ принадлежат одному показателю (имеют одинаковый порядок).

Показатель корней неприводимого полинома называется показателем, которому этот полином принадлежит. Если неприводимый полином $ F_(x) $ принадлежит показателю $ ell_ $, то он является делителем полинома $ x^-1 $, но не является делителем ни одного из полиномов $ x^k-1 $ при $ kin $. Неприводимый полином степени $ m_ $ над $ mathbf(p) $ называется примитивным, если его корнем является примитивный элемент поля $ mathbf(p^m) $. В этом случае, этот корень принадлежит показателю $ p^m-1 $, и по теореме 2, все корни $ F_(x) $ принадлежат тому же показателю, т.е. являются примитивными элементами поля.

Число неприводимых полиномов степени $ m_>1 $ равно $ phi (p^m-1)/m $.

Неприводимый полином $ F_(x) $ степени $ m_ $ является примитивным тогда и только тогда, когда он не является делителем ни одного из полиномов $ x^k-1 $ при $ kin $. Если каноническое разложение числа $ p^m-1 $ имеет вид:

$$ p^m-1=p_1^<_>p_2^<_>times dots times p_^<_<_>> , $$ то для того чтобы неприводимый полином $ F_(x) $ степени $ m_ $ был примитивным, необходимо и достаточно, чтобы он не являлся делителем ни одного из полиномов $ x^-1 $ при $ forall j in $.

Пример. Из трех неприводимых полиномов $ 4_ $-й степени: $$ x^4+x+1, x^4+x^3+1, x^4+x^3+x^2+x+1 $$ примитивными будут только первый и второй. Подробный разбор см. ☞ ЗДЕСЬ.

Пример. Примитивные полиномы $ 6_ $-й степени см. ☞ ЗДЕСЬ.

Видео:Горчинский С.О. - Теория Галуа - 1. Расширения полейСкачать

Источники

[1]. Чеботарев Н. Основы теории Галуа. Часть I. М.-Л.ОНТИ. 1934.

[2]. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.Мир. 1976.

[3]. Лидл Р., Нидеррайтер Г. Конечные поля. Том 1. М.Мир. 1988.

[4]. Ротман Т. Короткая жизнь Эвариста Галуа. Scientific American. N 1, 1983, cc. 84-93. Текст ☞ ЗДЕСЬ.

Видео:Канунников А. Л. - Начала теории Галуа - Расширение ГалуаСкачать

Арифметика полей Галуа для кодирования информации кодами Рида-Соломона

Коды Рида-Соломона относятся к недвоичным, блочным, помехоустойчивым кодам и могут использоваться в области хранения информации для избегания потери поврежденной информации.

На хабре есть пост посвященный кодированию информации кодами Рида-Соломона, но для примера автор использует простое поле Галуа. В данной статье описывается работа с расширенными полями Галуа, в частности GF(2^m), которые рационально использовать для цифровой информации. С моей аналогичной реализацией кодирования, декодирования, исправления ошибки можно ознакомится здесь.

При работе с кодами Рида-Соломона процент избыточных символов в 2 раза больше восстанавливаемого объема данных. Объясню на примере: если мы имеем последовательность из 10 символов и хотим иметь возможность восстановить ошибки в 3-ех из них (30% исходной информации), то нам нужно хранить 10+3*2=16 символов. Назовем каждую переменную: n = 10, количество информационных символов; f = 3, количество восстанавливаемых символов; g = 16, длина закодированной последовательности. Таким образом, формулу можно записать так: g = n + f * 2.

Поля Галуа

Для работы с информацией при кодировании и декодировании данных все арифметические операции выполняются в полях Галуа. Применяется так называемая полиномиальная арифметика или арифметика полей Галуа. Таким образом, результат любой операции также является элементом данного поля. Конкретное поле Галуа состоит из фиксированного диапазона чисел. Характеристикой поля называют некоторое простое число p. Порядок поля, т.е. количество его элементов, является некоторой натуральной степенью характеристики pm, где m∈N. При m=1 поле называется простым. В случаях, когда m>1, для образования поля необходим еще порождающий полином степени m, такое поле называется расширенным. GF(p^m) – обозначение поля Галуа.

Для работы с цифровыми данными естественно использовать p=2 в качестве характеристики поля. При m=1 элементом кодовой последовательности будет бит, при m=8 – 8 бит, то есть байт. Собственно коды Рида-Соломона работающие с байтами и являются наиболее распространенными.

Перед тем как переходить к операциям кодирования и декодирования разберемся с арифметикой полей Галуа на примере GF(2^3). Данное поле состоит из чисел от 0 до 7.

Операция сложения

Самой простой является операция сложения, которая является простым побитовым сложение по модулю 2 (ХОR).

Операция умножения

К сожалению, операция умножения гораздо сложнее, чтобы ее осуществить, необходимо преобразовать числа в полиномиальную форму.

Как можно заметить число в полиномиальной форме представляет собой многочлен, коэффициентами которого являются значения разрядов в двоичном представлении числа.

Перемножим два числа в полиномиальной форме:
5∙7=(x^2+1)∙(x^2+x+1)=x^4+x^3+x^2+x^2+x+1=x^4+x^3+x+1=11011=27

Итак, во-первых, следует заметить, что даже в полиномиальной форме осуществляется сложение по модулю 2, поэтому x^2+x^2=0. Во-вторых, результат умножения 27 не входит в используемое поле GF(2^3) (оно же состоит из чисел от 0 до 7, как было сказано выше). Чтобы бороться с этой проблемой, необходимо использовать порождающий полином. Порождающий полином является неприводимым, то есть простым (по аналогии с простыми числами делится без остатка на 1 и на самого себя). В арифметике полей Галуа неприводимым полиномом является аналог простых чисел. Используем для примера порождающий полином f(x)=x^3+x+1.

Также предполагается, что x удовлетворяет уравнению f(x)=x^3+x+1=0

Вернемся к примеру с умножением:

Составим таблицу умножения:

Операция деления

Операцию деления в полиномиальной форме понять, возможно, но достаточно тяжело. Поэтому гораздо лучше осуществлять его по таблице умножения.

Большое значение имеет таблица степеней элементов поля Галуа. Возведение в степень также осуществляется в полиномиальной форме, аналогично умножению.

Таким образом, составим таблицу степеней:

Таблица степеней обладает цикличностью: седьмая степень соответствует нулевой, значит восьмая соответствует первой и т.д. При желании можно это проверить.

В полях Галуа существует понятие примитивного члена – элемент поля, чьи степени содержать все ненулевые элементы поля. Просмотрев таблицу степеней видно, что этому условию соответствуют все элементы (ну кроме 1 естественно). Однако это выполняется не всегда, для примера приведу таблицу степеней для GF(16).

Для полей, которые мы рассматриваем, то есть с характеристикой 2, в качестве примитивного члена всегда выбирают 2. Учитывая его свойство, любой элемент поля можно выразить через степень примитивного члена.
Пример: 5=26, 7=25

Воспользовавшись этим свойством, и учитывая цикличность таблицы степеней, попробуем снова перемножить числа:
5∙7=2^6∙2^5=2^(6+5)=2^11=2^(11 mod 7)=2^4=6
Результат совпал с тем, что мы вычислили раньше.

А теперь выполним деление:
6÷5=2^4÷2^6=2^(4-6)=2^(-2)=2^((-2)mod 7)=2^5=7
Полученный результат тоже соответствует действительности.

Ну и для полноты картины посмотрим на возведение в степень:
5^2=(〖2^6)〗^2=2^(6∙2)=2^12=2^(12 mod 7)=2^5=7
Опять неожиданно получился такой же результат.

Такой подход к умножению и делению гораздо проще, чем реальные операции с использование полиномов, и для них нет необходимости хранить большую таблицу умножения, а достаточно лишь строки степеней примитивного члена поля.

Видео:18 Поля из 2, 3, 4, 5, 7, 8 и 9 элементовСкачать

Привет студент

Элементы теории Галуа

Дипломная РАБОТА

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Элементы теории Галуа

Аннотация

Цель дипломной работы является получить первые сведений о строении полей, об их простейших подполях и расширениях. Основными задачами являются рассмотрение групп Галуа, формулировка основной теоремы Галуа и самостоятельное решение задач предложенными авторами учебников.

Структура данной работы такова:

– первый раздел отражает теоретические основы и особенности полей, алгебраические расширения, конечные расширения, алгебраическое замыкание, расширение Галуа;

– второй разделе посвящен детальному изучению групп Галуа и основной теоремы Галуа;

– в третьем разделе рассмотрены приложения теории Галуа: решение уравнений в радикалах, построение с помощью циркуля и линейки, вычисление группы Галуа, так же приведены примеры по каждому из разделов и самостоятельно решены задачи, предложенные авторами учебников.

Работа выполнена печатным способом на 38 страницах с использованием 20 источников, содержит 15 теорем.

Содержание

1 Основные сведения о полях. 3

1.1 Расширения полей. 6

1.2 Алгебраическое замыкание. 11

1.3 Расширение Галуа. 13

2 Теория Галуа. 17

2.1 Группа Галуа. 17

2.2 Основная теорема Галуа. 22

3.1 Решение уравнений в радикалах. 26

3.2 Построения с помощью циркуля и линейки. 28

3.3 Вычисление группы Галуа. 31

Список литературы.. 38

Дипломная работа посвящена введению в один из самых красивых разделов математики – теорию Галуа.

Теория Галуа была разработана в начале 19 века для нахождения подполей алгебраических расширений. Сам Эварист Галуа писал, что он занимается анализом анализа. За прошедшее после создания время, теория Галуа, получила многочисленные приложения: построение с помощью циркуля и линейки; решение уравнений в радикалах; исследование вопроса о квадрируемости решений дифференциального уравнения и др.

Цель дипломной работы, изучить теорию Галуа и ее приложения. Для достижения поставленной цели необходимым решить следующие задачи: получить первые сведения о строении полей, об их простейших подполях и расширениях, а так же рассмотреть группы Галуа и основную теорему Галуа.

Самостоятельно решить задачи по теории Галуа. Так же привести примеры по соответствующим теоретическим сведениям.

Видео:Канунников А. Л. - Начала теории Галуа - Уравнения степени меньше 5Скачать

1 Основные сведения о полях

Полем называется целостное кольцо с единичным элементом е не равным нулю, в котором каждый ненулевой элемент имеет обрат­ный. В поле все ненулевые элементы образуют абелеву группу по умножению, называемую мультипликативной группой поля.

Определение: Кольцом называется непустое множество R на котором определены две операции – сложение и умножение, удовлетворяющих свойствам:

• Все элементы по сложению образуют абелеву группу с непустым элементом;
• Умножение дистрибутивно относительно сложения (слева и справа) (a+b)c=ac+cb, c(a+b)=ac+cb. Из однозначной разрешимости уравнения a+x=b следует, что дистрибутивность выполняется и относительно вычитания, умножение на нуль дает нуль: .

Типичный способ построения поля из целостного коль­ца — присоединение частных или нахождение кольца классов вычетов по максимальному идеалу [4].

Определение: Идеал I кольца A – это подмножество в A, являющееся подгруппой аддитивной группы A, такое, что AI ⊂ I, IA⊂ I [18].

Поле К не содержит идеалов, отличных от ну­левого и единичного (совпадающего с К). Дейст­вительно, пусть I — ненулевой идеал поля К. Тогда существует обратимый в К элемент а I. По определению идеала е = аа -1 I , и, следова­тельно, любой элемент поля К лежит в I.

• Множество Q рациональных чисел является полем частных кольца Z целых чисел. Мультип­ликативная группа Q поля Q состоит из ненуле­вых рациональных чисел. Множество четных чисел образует кольцо 2Z, поле частных которо­го в результате сокращения числителя и знаме­нателя на 2 тоже совпадает с полем Q. Анало­гично, множество рациональных чисел является полем частных любого кольца вида nZ для цело­го n.
• Кольцо Z[i] =Z+Zi содержит Z, поэтому его поле частных К должно содержать всевоз­можные рациональные числа Q, а также мнимую

единицу i как дробь . Покажем, что К = Q(i) = Q + Qi. Действительно, частное = = +

имеет вид g + hi, где g, h — рациональные числа. Обратно, любое число вида g + hi с рациональ­ными g, h может быть представлено как частное элементов кольца Z[i]. Пусть g = , h = , где r, s, t, и Z. Тогда можно записать

g + hi = , где числитель и знаменатель являются элемента­ми кольца Z[i] [4]. ■

Определение: Биективный гомоморфизм колец называется изоморфизмом колец [18].

Все гомоморфизмы полей инъективны (на­пример, гомоморфное вложение поля Q в поле R) или биективны (в противном случае в поле существовал бы собственный ненулевой идеал, что невозможно).

Если К— произвольное поле и его подмно­жество k тоже является полем, то k называется подполем поля К. Поскольку любое поле содер­жит не менее двух элементов (0 и е), каждый из которых единственный, то пересечение двух подполей поля К является полем. Очевидно, что пересечение любого числа подполей поля К вновь является полем.

Простым называется поле, не содержащее собственных подполей.

Теорема 1. Каждое поле содержит одно и только одно простое подполе.

Доказательство. Пересечение всех подпо­лей поля К является подполем, не имеющим соб­ственных подполей. Предположим, что сущест­вуют два различных простых подполя. В этом случае пересечение этих подполей было бы соб­ственным подполем в каждом из них. Следова­тельно, эти подполя— не простые. Противоре­чие доказывает теорему. ■

Теорема 2. Простое поле изоморфно кольцу Z/pZ, где — простое число, или полю Q рациональных чисел.

Доказательство. Пусть К— простое под­поле поля L. Поле К содержит нуль и единицу е и, следовательно, кратные единичного элемента пе = е + е + . + е. Сложение и умножение этих кратных осуществляется по правилу пе + те =

=(п + т)е, (пе)(те) = = пте 2 = пте. Следователь­но, целочисленные кратные пе образуют комму­тативное кольцо Р. Отображение п —> пе задает гомоморфизм кольца Z на кольцо Р. По определению о гомоморфизмах колец Р = Z/ I, где I — идеал, состоящий из тех целых чисел n, которые дают равенство пе = 0.

Кольцо Р целостное, так как поле К — цело­стное кольцо. Поэтому и Z/ I тоже целостное. Кроме того, идеал I не может быть единичным, так как иначе выполнялось бы 1 ∙ е = 0. Следова­тельно, существуют только две возможности:

• I = (р), где р — простое число. В этом случае р является наименьшим положительным числом, для которого ре = 0. Ядро гомоморфизма содержит целые числа, кратные р — это идеал (р) или, в другой записи, рZ. Поэтому

Простейшее простое поле состоит из двух элементов, 0 и 1. Таблица сложения и умножения имеет вид:

0 + 0 = 0, 0 + 1 = 1, 1 + 0=1, 1 + 1 = 0,

0 ∙ 0 = 0,0 ∙ 1 = 0, 1∙ 0 = 0, 1 ∙ 1 = 1.

2) I = (0). Тогда гомоморфизм Z→ Р являет­ся изоморфизмом. Кратные пе все попарно раз­личны: если пе = 0, то п = 0. В этом случае коль­цо Р не является полем, так как Z не является полем. Простое поле К должно содержать не только элементы из Р, но и их частные. В этом случае целостные кольца Р и Z имеют изоморф­ные поля частных. Поэтому простое поле К изо­морфно полю Q рациональных чисел. [10] ■

Таким образом, строение содержащегося в L простого поля К с точностью до изоморфизма определяется заданием простого числа р или числа 0, которые порождают идеал I, состоящий из целых чисел п со свойством пе = 0. Число п называется характеристикой поля L и обознача­ется char(L). При этом char(L) = char(K).

Теорема 3. В полях характеристики р имеют место равенства

Доказательство. По формуле бинома Нью­тона имеем

Здесь все коэффициенты, кроме первого и по­следнего, делятся на р, так как числитель у них делится на р. Поскольку р — характеристика по­ля, то в рассматриваемом поле все эти слагаемые равны нулю, то есть

Аналогично рассуждаем и в случае разности. Положим с = а + b. Тогда

Если р — нечетное число, то число слагаемых в формуле бинома Ньютона четное и коэффици­ент при b р равен -1. Если р = 2, то коэффициент при b р равен 1. Отсюда заключаем, что в поле характеристики 2 выполняется равенство — 1 = 1 [7].

1.1 Расширения полей

Пусть К— подполе поля L. Тогда L называет­ся расширением поля К. Расширение L поля К будем обозначать L⊂ K. Рассмотрим строение расширения L.

Пусть L— расширение поля К, S— произ­вольное множество элементов из L. Существует поле, содержащее в себе (как в множестве) поле К и множество S (таким полем является, например, L). Пересечение всех полей, содержащих К и S, является полем, причем наименьшим из полей, содержащих в себе К и S, и обозначается K(S). Говорят, что K(S) получается присоединением множества S к полю К. Имеет место включение

Полю K(S) принадлежат все элементы из К, все элементы из S, а также все элементы, полу­ченные при сложении, вычитании, умножении и делении этих элементов, то есть K(S) состоит из всех рациональных комбинаций , где . (Отсюда следует, что множество S можно выбирать различными способами.) Эти рациональные комбинации могут быть записаны как рациональные функции, то есть как отноше­ния полиномов, где переменные— элементы множества S, а коэффициенты полиномов — элементы поля К.

Таким образом, для любого поля можно построить расширение.

Видео:34 Построение конечных полейСкачать

Расширение, полученное присоединением од­ного элемента, называется простым [3].

1.1.1 Конечные расширения

Поле L называется конечным расширением поля К, если L является конечномерным вектор­ным пространством над К [6]. При этом все элемен­ты из L являются линейными комбинациями ко­нечного множества элементов u₁,…,u_n с коэф­фициентами из К. Число элементов базиса век­торного пространства называется степенью рас­ширения L над К и обозначается (L:K).

Элемент w ∊ L называется алгебраическим над К, если он удовлетворяет алгебраическому уравне­нию f(w) = 0 с коэффициентами из К. Расширение L поля К называется алгебраическим над К, если каж­дый элемент поля L является алгебраическим над К.

Теорема 5. Каждое конечное расширение L поля К получается присоединением к К конечного числа алгебраических над К элементов. Каждое расширение, полученное присоединением конеч­ного числа алгебраических элементов, конечно.

Доказательство. Пусть поле L является ко­нечным расширением поля К, и степень расши­рения равна п. Пусть w ∊ L⊂ K. Тогда среди сте­пеней

w 0 =е,w,. w n не более n линейно неза­висимых. Значит, должно выполняться равенство а₀ + а₁ w + . + a_n w n = 0, при a_i ∊ К, то есть каж­дый элемент поля L алгебраичен над К. Обратно, пусть w— алгебраический элемент степени r. Тогда элементы е, w,. w r -1 линейно независи­мы и образуют базис, то есть расширение явля­ется конечным. ■

1.1.2 Алгебраические расширения

Пусть K—подполе поля L [8]. Элемент α из L называется алге­браическим над K, если в K существуют элементы а₀,…,а_п (n≥1) не все равные 0 и такие, что

Для алгебраического элемента α не равно нулю мы всегда можем найти такие элементы a_i в предыдущем равенстве, что а₀ не равно нулю (сокращая на под­ходящую степень α).

Пусть X — переменная над K. Можно также сказать, что эле­мент α алгебраичен над K, если гомоморфизм K[X]→L , тождественный на K и переводящий из X в α, имеет ненулевое ядро. В таком случае это ядро будет главным идеалом, порожденным одним многочленом р(Х), относительно которого мы можем предполагать, что его старший коэффициент равен 1. Имеет место изоморфизм

и так как кольцо K[a] целостное, то р(X) неприводим. Если р(Х) нормализован условием, что его старший коэффициент равен 1, то р(Х) однозначно определяется элементом α и будет называться не­приводимым многочленом элемента α над K. Иногда мы будем обо­значать его через Irr(α,K,X).

Расширение Е поля K называется алгебраическим, если всякий элемент из Е алгебраичен над K.

Предложение 1. Всякое конечное расширение Е поля K алгебраично над K.

Доказательство. Пусть а Е, α≠ 0. Степени α

не могут быть линейно независимы над K для всех целых положи­тельных п, иначе размерность Е над K была бы бесконечна. Линей­ное соотношение между этими степенями показывает, что элемент α алгебраичен над K.

Заметим, что утверждение, обратное предложению, не верно: существуют бесконечные алгебраические расширения. Позднее мы увидим, что подполе поля комплексных чисел, состоящее из всех чисел, алгебраических над Q, является бесконечным расширением Q. Если Е—расширение поля K, то мы обозначаем символом L ⊂ K, размерность Е как векторного пространства над K. Будем называть (Е: K) степенью Е над K. Она может быть бесконечной.

Степень неприводимого над К полинома р(х) с корнем α называется степенью элемента α. Если степень элемента α равна 1, то α является элемен­том поля К, то есть по существу расширения нет.

Назовем два расширения L и L‘ поля К изо­морфными (над К), если существует изоморфизм L L‘, оставляющий неподвижными элементы поля К.

Простые алгебраические расширения можно строить и не прибегая к включающему K( α) полю L. При этом алгебраическое расширение изоморфно кольцу классов вычетов K[x]/(р(х)). Следовательно, ал­гебраическое расширение однозначно определя­ется полиномом р(х).

1.2 Алгебраическое замыкание

Поле L называется алгебраически замкнутым, если каждый полином из L[x] раскладывается на линейные множители [6]. Алгебраически замкнутое поле не допускает дальнейших алгебраических расширений. Поэтому можно говорить о макси­мальном алгебраическом расширении данного поля. Примером алгебраически замкнутого поля является поле С комплексных чисел.

Каждое поле К обладает единственным с точ­ностью до изоморфизма алгебраически замкну­тым алгебраическим расширением. Такое од­нозначно определенное алгебраическое расши­рение называется алгебраическим замыканием поля К.

Поле L называется алгебраически замкнутым, если всякий мно­гочлен из L[X] степени ≥ 1имеет в L корень.

Теорема 6. Для всякого поля K существует алгебраически замкнутое поле L, содержащее K в качестве подполя.

Доказательство. Сначала мы построим расширение Е₁ поля K, в котором всякий многочлен из K [X] степени ≥1 имеет корень. Можно действовать следующим образом , каждому много­члену f из K [X] степени ≥1 сопоставим символ X_f. Пусть S—мно­жество всех таких символов X_f (так что S находится в биективном соответствии с множеством многочленов из K[X] степени ≥1). Обра­зуем кольцо многочленов K [S]. Мы утверждаем, что идеал, поро­жденный всеми многочленами f(X_f ) в K [S], не является единичным. Если бы это было не так, то существовала бы конечная комбинация элементов из нашего идеала, равная 1:

Пусть F— конечное расширение, в котором каждый многочлен

По индукции мы можем построить такую последовательность полей

Пусть Е — объединение всех полей Е_n, n= 1, 2,…Тогда Е, естественно, является полем, поскольку для любых х, у ∊ Е найдется номер n, такой, что х, у∊ Е_п, и мы можем взять произведение ху или сумму х+у в Е_п. Эти операции, очевидно, не зависят от вы­бора того п, для которого х, у∊ Е_п, и определяют структуру поля на Е. Всякий многочлен из Е[X] имеет коэффициенты в некотором подполе Е_п и, следовательно, обладает корнем в Е_п+1 ,а тем самым и корнем в Е, что и требовалось доказать.

Следствие. Для всякого поля K существует расширение K, алгебраическое над K и алгебраически замкнутое.

Теорема 7. Пусть K — поле, Е—его алгебраическое расши­рение и

F ⊂ F‘и τ’|F = τ. Отметим, что множество S не пусто, оно содержит (K,σ), и индуктивно упорядочено: если <(F_i , τ_i)> линейно упорядоченное подмножество, то положим F= F_i и опре­делим τ на F, положив его равным τ_i на каждом F_i . Тогда (F, τ) служит верхней гранью для этого линейно упорядоченного подмно­жества. Находим (К, λ)—максимальный эле­мент в S. Тогда λ есть продолжение σ, и мы утверждаем, что К=Е. В противном случае существует α∊Е, α∉ К; в силу предыдущего вложение λ имеет продолжение на К (α) вопреки максимальности (К, λ). Таким образом, существует продолжение σ на Е. Мы обо­значаем это продолжение снова через σ.

В качестве следствия получаем некую теорему единственности для «алгебраического замыкания» поля K.

Следствие. Пусть K — поле и Е, Е’—алгебраические рас­ширения над K. Предположим, что Е, Е’ алгебраически замкнуты. Тогда существует изоморфизм

1.3 Расширение Галуа

Расширения поля К, получаемые присоединением корней раз­личных неприводимых многочленов, могут оказаться изоморфными или, более общее, одно из них может изоморфно вкладываться в другое [11]. Выяснить, когда это имеет место, не так просто. Изучением гомоморфизмов алгебраических расширений полей как раз и занимается теория Галуа.

Пусть L — конечное расширение степени п поля К. Автомор­физмы поля L над К образуют группу, которую мы обозначим через Aut α _K L.

Пусть G Aut α _K L— какая-то (конечная) группа автоморфизмов поля L над К. Обозначим через L G подполе G-инвариантных элементов поля L.

Определение : Расширение L поля К называется нормальным над полем К или расширением Галуа, если оно во-первых, алгебраично над К и, во-вторых, каждый неразложимый в К[x] многочлен g(x), обладающий в L хоть одним корнем α, разлагается в L[x] на линейные множители.

Если α – корень неразложимого в кольце К[x] многочлена, обладающего лишь простыми корнями, то α называется сепарабельным элементом над К или элементом первого рода над К. При этом неразложимый многочлен, все корни которого сепарабельны, называется сепарабельным. В противном случае алгебраический элемент α и неразложимый многочлен g(x) называются несепарабельными или элементом (соответственно, многочлен) второго рода.

Определение: Алгебраическое расширение L, все элементы которого сепарабельны над К, называется сепарабельным над К, а любое другое алгебраическое расширение называется несепарабельным.

Группа Aut α _KL называется группой Галуа расшире­ния L и обозначается через Gal L/ K.

Обозначим через f” формальную производную многочлена f.

Предложение 2.3.1: Многочлен f ∊ К[х] сепарабелен тогда и только тогда, когда (f, f‘) = 1.

Доказательство. Заметим, прежде всего, что наибольший общий делитель любых двух многочленов f, g ∊ К[х] может быть найден с помощью алгоритма Евклида и потому не изменяется при любом расширении поля К.

С другой стороны, если над каким-либо расширением L поля К многочлен f имеет кратный неприводимый множитель h, то h | f‘ в L[x] и, значит, (f,f’)≠1. В частности, это будет иметь место, если f имеет кратный корень в L.

Обратно, если (f, f‘) ≠ 1, то какой-то неприводимый множитель h многочлена f над К делит f’. Это возможно только в двух случаях: если h — кратный неприводимый множитель и если h’ = 0. В первом случае многочлен f имеет кратный корень в некотором расширении поля К (в частности, если h линеен, то в самом поле К). Второй случай имеет место, только если charК=р> 0 и многочлен h имеет вид

и, следовательно, в некотором расширении поля L многочлен h, а значит, и f, имеет кратный корень.

Следствие 1: Всякий неприводимый многочлен над полем ну­левой характеристики сепарабелен.

Следствие 2: Всякий неприводимый многочлен f над полем характеристики p/degf сепарабелен.

Следствие 3: Всякий неприводимый многочлен над конечным полем сепарабелен.

Доказательство. Пусть h — несепарабельный неприводи­мый многочлен над конечным полем К. Тогда он имеет вид (7). Так как К р = К , то существуют такие b₀, b_l:. b_m ∊ К, что b_K p = а_к и, значит, h представляется в виде (8) уже в К[х], что противоречит его неприводимости.

Примером несепарабельного неприводимого многочлена может служить многочлен

x p — α=(x- α) p над полем pZ(α). (9)

Теорема 7. Пусть f∊ К[х] — многочлен, все неприводимые множители которого сепарабельны. Тогда его поле разложения над К является расширением Галуа.

Доказательство. Заметим, что если L — поле разложения многочлена f ∊ К[х], то любой автоморфизм φ поля L над К сохраняет множество <φ₁. φ_n> корней многочлена f, каким-то образом их перестав­ляя. Так как

L = K(φ₁. φ_n), то автоморфизм φ однозначно определяется той перестановкой, которую он осуществляет на мно­жестве корней. Тем самым группа Aut α _K L изоморфно вкладывается в S_n.

Пример 3. Как следует из формулы для решения квадратного уравнения, всякое квадратичное расширение поля К характеристи­ки не равной 2 имеет вид K( d), где d ∊ К⊂К 2 . Всякое такое расшире­ние является расширением Галуа. Его группа Галуа порождается автоморфизмом а + b d → а — b d (а, b ∊ К).

Видео:Построение поля из 4 элементов. Бардаков Валерий ГеоргиевичСкачать

2 Теория Галуа

2.1 Группа Галуа

Видео:Как решают уравнения в России и США!?Скачать

Теория Галуа занимается конечными сепарабельными расши­рениями поля К и, в частности, их изоморфизмами и автомор­физмами [12]. В ней устанавливается связь между расширениями дан­ного поля К, содержащимися в фиксированном нормальном рас­ширении этого поля, и подгруппами некоторой специальной конечной группы. Благодаря этой теории оказывается возможным ответить на различные вопросы о разрешимости алгебраических уравнений.

Видео:Как распознать талантливого математикаСкачать

Все тела, рассматриваемые в этой главе, считаются коммута­тивными. После К будет называться основным.

Если задано основное поле К, то каждое ко­нечное сепарабельное расширение L этого поля порождается некоторым «примитивным элементом» Ѳ: L = К(Ѳ). Расширение L имеет в некотором подходяще выбранном расшире­ний столько же изоморфизмов над К, т. е. изоморфизмов, оставляющих все элементы из К на месте, какова степень n рас­ширения L поля К. В качестве такого расширения P можно взять поле разложения многочлена f (х), корнем которого явля­ется элемент Ѳ. Такое поле разложения является наименьшим над К нормальным расширением, содержащим поле L, или, как мы еще будем говорить, P является нормальным расширением, соответствующим полю L. Изоморфизмы расширения К/Ѳ над К могут быть определены благодаря тому обстоятельству, что эле­мент Ѳ переводится ими в сопряженные элементы Ѳ₁,. Ѳ_n поля P. Каждый элемент φ(θ) = ∑ a_λ θ λ (a_λ ϵ К) переходит тогда в φ(θ_V) = ∑ a_λ θ λ _V и поэтому вместо того, чтобы говорить об изоморфизме,

можно говорить о подстановке θ → θ_V .

Необходимо, однако, обратить внимание на то, что элементы θ и θ_V являются лишь вспомогательным средством, де­лающим более удобным представление изоморфизмов, и что понятие изоморфизма совершенно не зависит от того или иного вы­бора элемента θ.

Теорема 8. Если L — нормальное расширение, то все сопряженные поля К(θ_V) совпадают с L.

Доказательство: Действительно, прежде всего, в этом случае все θ_V cодержатся в К(θ). Но К (θ_V) эквивалентно К (θ), а потому является нормальным. Следовательно, и наоборот, элемент θ содержится в каждом поле К (θ_V).

Обратно: если L совпадает со всеми полями L(θ_V), то расши­рение L нормально.

Будем впредь считать, что L = К /θ — нормальное расширение. В этом случае изоморфизмы, переводящие L в сопряженное с ним поле К/θ_V, оказываются автоморфизмами поля L. Эти автоморфизмы поля L (оставляющие неподвижным каждый элемент из К) составляют группу из n элементов, которая назы­вается группой Галуа поля L над полем К или относительно К. В наших последующих рассмотрениях эта группа играет главную роль. Будем обозначать ее через G. Порядок группы Галуа равен степени расширения п = (L : К).

Когда в некоторых случаях речь заходит о группе Галуа ко­нечного сепарабельного расширения L ‘, не являющегося нормаль­ным, подразумевается группа Галуа соответствующего нормаль­ного расширения L ϶ L‘.

Для отыскания автоморфизмов совсем нет необходимости искать примитивный элемент расширения L. Можно построить L путем нескольких последовательных присоединений: L = К (α₁, . α_m), затем найти изоморфизмы поля К (α₁), которые перево­дят α₁ в сопряженные с ним элементы, после этого продолжить полученные изоморфизмы до изоморфизмов поля К (α₁, α₂) и т. д.

Важным частным случаем является такой, когда α₁, . α_m — это все корни некоторого уравнения f(x) = 0, не имеющего крат­ных корней. Под группой уравнения f(x) = 0 или многочлена f(x) подразумевается группа Галуа поля разложения К(α₁, . α_m) этого многочлена [5]. Каждый автоморфизм над полем К переводит систему корней в себя, т. е. переставляет корни. Если такая пере­становка известна, то известен и автоморфизм, потому что если, например, α₁, . α_m переходят в ά1, . ά_m, то каждый элемент из

К(α₁, . α_m), как рациональная функция φ(α₁, . α_m), пе­реходит в соответствующую функцию φ(ά1, . ά_m). Следовательно, группу уравнения можно рассматривать как группу некоторых подстановок корней. Именно эта группа подстановок будет всегда подразумеваться, когда речь зайдет о группе какого-либо урав­нения.

Пусть A — некоторое «промежуточное» поле: К A L. Каждый изоморфизм поля A над К, пере­водящий A в сопряженное с ним поле A‘ внутри L, можно про­должить до некоторого изоморфизма поля L, т. е. до некоторого элемента группы Галуа. Отсюда следует утверждение.

Два промежуточных поля A, A‘ сопряжены над К тогда и только тогда, когда они переводятся друг в друга некоторой подстановкой из группы Галуа.

Положим A = К(α); тогда точно так же получается утвержде­ние:

Два элемента α, α’ поля L сопряжены друг с другом над К тогда и только тогда, когда они переводятся друг в друга неко­торой подстановкой из группы Галуа поля L.

Если уравнение f(x) = 0 неразложимо, то все его корни со­пряжены, и наоборот. Следовательно,

Группа уравнения f(x) = 0 транзитивна тогда и только тогда, когда уравнение неразложимо над основным полем.

Число различных сопряженных с α элементов поля L равно степени неразложимого уравнения, определяющего α. Если это число равно 1, то α является корнем линейного уравнения и поэтому содержится в К. Следовательно,

Теорема 9. Если элемент α поля L остается неподвижным при всех под­становках из группы Галуа поля L, т. е. переводится всеми под­становками в себя, то основное поле К содержит α.

Расширение L поля К называется абелевым, если его группа Галуа абелева, циклическим, если его группа Галуа циклична, и т. д. точно так же уравнение называется абелевым, циклическим, примитивным, если его группа Галуа абелева, циклическая или (как группа подстановок корней) примитивная.

Задача 1. Найти группу Галуа уравнения x 2 + px + q = 0, если F, char F 2.

На множестве корней f(x), задаются подстановкой.

3 а д а ч а 2. С помощью квадратных и кубических корней решить урав­нения

и построить их группы Галуа.

• Пусть f(x) = х 3 — 2. Корни уравнения могут быть найдены по формуле Муавра.

Q( )= Q( ) ⊂ R, многочлен х 2 — 2 не приводимый над Q

Минимальный многочлен х 3 — 2 ⇒ (K : Q)=(K: Q( ))( Q( )= 3 2 = 9.

Базис расширения Q ⊂ K

Группа Aut _Q K являются произведением двух циклических подгрупп порядка 3.

x 2 = t, t 2 = 5t+6 ⇒ 5t+6=0 ⇒ t₁=2, t₂=3

( ) 2 – 3 = 0 многочлен х 2 — 3 является минимальным многочлена

(Q( ): Q)= (Q( ): Q ) (Q( : Q))= 2

Базисом Q( ) над Q являются числа: 1, ,

Q ⊂ (Q( )) – расширение Галуа. Число элементов группы автоморфизмов |Aut_Q Q( ) |= 4. Обозначим элементы |Aut_Q Q( ) | тождественно(id) Этим автоморфизмам соответствует следующие подстановки корней f(x):

2.2 Основная теорема Галуа

• Каждому промежуточному полю A,K⊆A⊆L, соответ­ствует некоторая подгруппа g группы Галуа G, а именно, сово­купность тех автоморфизмов из которые оставляют на месте все элементы из A.
• Поле A определяется подгруппой g одно­значно; именно, поле A является совокупностью тех элементов из L, которые «выдерживают» все подстановки из g, т. е. оста­ются инвариантными при этих подстановках.
• Для каждой подгруппы g группы G можно найти поле A, которое находится с подгруппой g в только что описанной связи.
• Порядок под­группы g равен степени поля L над полем A; индекс подгруппы g в группе G равен степени поля A над полем К.

Доказательство. Совокупность автоморфизмов поля L, оставляющих на месте каждый элемент из A, является группой Галуа поля L над A, т. е. некоторой группой. Тем самым дока­зано утверждение 1. Утверждение 2 следует из тео­ремы 9, примененной к L как расширению и A как основ­ному полю.

Пусть опять L = К (θ) и пусть g — заданная подгруппа группы G. Обозначим через A совокупность элементов из L, которые при всевозможных подстановках σ из g переходят в себя. Очевидно, множество A является полем, потому что если αиβ остаются неподвижными при подстановке σ, то неподвижными при этой подстановке будут и α + β, α —β, α β, и, в случае β≠0, α/β.

Далее, имеет место включение K⊆A⊆∑. Группа Галуа поля L над полем A содержит подгруппу g, так как подстановки из g оставляют неподвижными элементы из A. Если бы группа Галуа поля L над A содержала больше элементов, чем входит в g, то степень (L : A) была бы больше, чем порядок подгруппы g. Эта степень равна степени элемента θ над полем A, так как L=A(θ). Если σ₁ . σ_h — подстановки из g, то θ является одним из кор­ней уравнения h—й степени

коэффициенты которого остаются инвариантными при действии группы G, а потому принадлежат полю A. Следовательно, степень элемента θ над A не больше, чем порядок подгруппы g. Таким образом, остается лишь одна возможность: подгруппа g является в точности группой Галуа поля L над полем A. Тем самым утверждение 3 доказано.

Если n —порядок группы G, h —порядок подгруппы g и j — индекс этой подгруппы, то

Утверждение 4 доказано.

Согласно только что доказанной теореме связь между под­группами g и промежуточными полями A является взаимно однозначным соответствием. Нахождение подгруппы g, когда известно A, и как найти A, когда известна подгруппа g. Предположим, что уже найдены сопря­женные с θ элементы θ₁. θ_n, выраженные через θ: тогда у нас есть автоморфизмы θ → θ_V, которые исчерпывают группу G. Если теперь задано подполе A = К(β₁. β_k), где β₁. β_k — известные выражения, зависящие от θ, то g состоит просто из тех подстановок группы G, которые оставляют инвариантными элементы β₁. β_k, потому что такие подстановки оставляют инвариантными все рациональные функции от β₁. β_k.

Обратно, если задана подгруппа g, то составим соответствую­щее произведение

Коэффициенты этого многочлена, согласно основной теореме, должны принадлежать полю A и даже порождать поле A, потому, что они порождают поле, относительно которого элемент θ, как корень уравнения (10), имеет степень h, а быть собственным расширением для A это поле не может. Следовательно, образую­щие поля A являются просто элементарными симметрическими функциями от σ₁θ,…, σ_h θ.

Другой метод состоит в том, чтобы отыскивать элемент который при подстановках из g остается неподвижным, но ника­ких других подстановок из G не выдерживает. Тогда элемент x(θ) принадлежит полю A, но не принадлежит никакому собст­венному подполю поля A; тем самым этот элемент порождает A.

С помощью основной теоремы теории Галуа получается пол­ное описание промежуточных между K и L полей, когда из­вестна группа Галуа. Число таких полей конечно, по­тому что конечная группа имеет лишь конечное число подгрупп. Об отношении включения между различными полями можно судить по соответствующим группам.

Теорема 11. Если A₁ — подполе поля A ₂, то группа g₁, соответствующая полю A ₁, содержит группу соответствующую полю g₂, и наоборот.

Доказательство. Пусть сначала A ₁⊆ A ₂. Тогда каждая подстановка, оставляющая на месте элементы из A ₂, оставляет на месте и элементы из A ₁.

Пусть, далее, g₁ ⊇ g₂. Тогда каждый элемент поля, который выдерживает все подстановки из g₁ выдерживает и все подста­новки из g₂.

Определение: Нормальное расширение L поля K называется циклическим расширением, если его группа Галуа является циклической группой.

Задача 1. Если L — циклическое расширение поля К степени n, то для каждого делителя d числа п существует ровно одно промежуточное расшире­ние A степени d и два таких промежуточных поля содержатся друг в друге тогда и только тогда, когда степень одного из них делится на степень другого.

Решение. Циклическим называется расширение Галуа с циклической группой Галуа. По свойствам циклической группы для каждого d|n существует ровно одна подгруппа порядка d. Следовательно, согласно основной теореме теории Галуа, для каждого числа d делящего n существует ровно одно расширение порядка d.

Утверждение о том, что два таких расширения содержатся друг в друге тогда и только тогда, когда степень делит степень другого, также является следствием основной теоремы теории Галуа.

Задача 2. С помощью теории Галуа заново определить подполя в GF(2 6 ).

Решение. Автоморфизм Фробелиуса α→α 2 порождает группу Галуа порядка 6 поля K. Циклическая группа порядка 6 имеет две подгруппы порядка 2 и 3. Им соответствуют подполя GF(2 3 ) и GF(2 2 ). Структура подполей имеет вид: GF(2 6 )

GF(2)
3 Приложения теории Галуа

3.1 Решение уравнений в радикалах

Расширение Е поля F называется радикальным расширением, если существуют промежуточные поля F = В₀, В₁, В₂, . B_r = Е и

–α_i=0, α_i ϵ B_i-1 . Многочлен f(x) над полем F называется раз­решимым в радикалах, если его поле разложения лежит в некотором радикальном расширении. Мы предполагаем, если не оговорено против­ное, что характеристика основного поля равна нулю и что F содержит столько корней из единицы, сколько нам необходимо для справедливости наших дальнейших утверждений [14].

Заметим вначале, что любое радикальное расширение поля F все­гда можно продолжить до нормального радикального расширения над F. Действительно, В₁ — нормальное расширение поля В₀, поскольку оно содержит не только α₁ но и εα₁ где ε — любой корень степени п₁ из едини­цы, откуда следует, что В₁ — поле разложения многочлена х п 1 — α₁ . Если f₁(x)= , где принимает все значения в группе автоморфизмов поля В₁ над B₀ , то f₁ лежит в В₀; присоединяя последовательно корни уравнения ), мы придем к расширению B₂, нормальному над F. Продолжая действовать таким образом, мы придем к радикаль­ному расширению E, которое будет нормальным над F.

Определение: Пусть F содержит примитивный корень степени n из единицы. Любое поле разложения E многочлена

Теорема 12. Многочлен f(x) разрешим в радикалах, если и только если его группа разрешима.

Предположим, что f(x) разрешим в радикалах. Пусть Е — нор­мальное радикальное расширение поля F, содержащее поле разло­жения В многочлена f(x). Обозначим через G группу поля Е над F. Поскольку для каждого i поле В_i, является куммеровым расширением поля B_i-1 , группа поля B_i над B_i-1 абелева. В последовательности групп G = . = 1 каждая подгруппа нормальна в преды­дущей, поскольку — группа поля Е над

B_i-1, а B_i — нормальное расширение группы B_i-1 . Но / — группа поля B_i над B_i-1 и потому она абелева. Следовательно, G разрешима. С другой стороны, G_B — нормальная подгруппа группы G, a G/G_B — группа поля В над F и, тем самым, группа многочлена f(x). Группа G/G_B является гомоморфным образом разрешимой группы G и потому сама разрешима.

Теперь предположим, что группа G многочлена f(x) разрешима, и пусть Е — его поле разложения. Пусть G = . = 1 — последовательность групп с абелевыми присоединенными факторами. Обозначим через В_i неподвижное поле для группы G_i. Поскольку G_i-1 — группа поля Е над B_i-1 и G_i— нормальная подгруппа группы G_i-1 по­ле B_i нормально над B_i-1 и группа G_i-1/G_i абелева. Таким образом, B_i является куммеровым расширением поля B_i-1, а значит, оно является полем разложения многочлена вида (х п — α₁)(х п — α ₂). (х п — α _s). По­следовательно строя поля разложения многочленов х п — α_k, мы видим, что B_i — радикальное расширение поля B_i-1, откуда следует, что и само Е является радикальным расширением.

Предположение, что F содержит корни из единицы, не является необходимым в доказанной теореме. Действительно, если мно­гочлен f(x) обладает разрешимой группой G, то мы можем присоединить к F примитивный корень степени п из единицы, где n, скажем, равно порядку группы G. Группа многочлена f(x), рассматриваемого как много­член над полем , по теореме о естественных иррациональностях явля­ется подгруппой G’ группы G, и поэтому она разрешима. Таким образом, поле разложения многочлена f(x) над F’ можно получить с помощью присоединения радикалов. Обратно, если поле разложения Е многочле­на f(x) над F можно получить с помощью присоединения радикалов, то, присоединяя подходящий корень из единицы, мы получим расширение Е’ поля E, которое все еще нормально над F. Но поле Е’ можно было бы получить также присоединяя сперва к полю F корень из единицы, а затем радикалы; сначала бы мы получили расширение F’ поля F, а затем от F’ перешли бы к Е’. Обозначая через G группу поля Е’ над F и че­рез G’ — группу поля Е’ над F’, мы видим, что группа G’ разрешима и что G/G’ — группа поля F’ над F, а потому она абелева. Поэтому группа G разрешима. Факторгруппа G/G_E является группой многочлена f(x) и, будучи гомоморфным образом разрешимой группы, сама разрешима [9].

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

3.2 Построения с помощью циркуля и линейки

Предположим, что на плоскости задано конечное число элементар­ных геометрических фигур, т. е. точек, прямых и окружностей. Наша задача — найти способ построения других фигур, удовлетворяющих не­которым условиям относительно фигур, заданных изначально.

Допустимыми операциями в таких конструкциях являются выбор произвольной точки, лежащей внутри заданной области, проведение прямой, проходящей через две точки, построение окружности с данным центром и радиусом и, наконец, построение точек пересечения пары прямых, окружностей или прямой и окружности [20].

Поскольку прямая или отрезок определяются двумя своими точками, а окружность — тремя своими точками или центром и одной точкой, построение циркулем и линейкой можно рассматривать как нахожде­ние точек, удовлетворяющих некоторым условиям, по другим заданным точкам.

Если нам даны две точки, то мы можем соединить их прямой, восстановить перпендикуляр к этой прямой в одной из данных точек и, принимая расстояние между некоторыми двумя точками за единицу, с помощью циркуля отложить любое целое расстояние n на прямой [1]. Более того, применяя стандартный прием, мы можем проводить параллельные прямые и строить частное т/п. Используя пару прямых в качестве осей декартовой системы координат, с помощью циркуля и линейки мы можем построить все точки с рациональными координатами.

Если а, b, с, . — числа, являющиеся координатами точек, которые определяют заданные фигуры, то можно построить сумму, произведение, разность и частное любой пары этих чисел. Итак, можно построить лю­бой элемент поля Q(a, b, с, . ), которое порождают эти числа над полем рациональных чисел.

Мы можем выбрать произвольную точку заданной области. Если построение циркулем и линейкой возможно, то мы всегда можем выбрать наши произвольные точки так, чтобы их координаты были рациональ­ны. Если соединить прямой две точки, координаты которых принадлежат полю Q(a,b,с,. ), то коэффициенты уравнения этой прямой будут при­надлежать Q(a, b, с, . ), и координаты точки пересечения двух таких прямых также будут принадлежать полю Q (a, b, с, . ). Если окруж­ность проходит через три точки с координатами из того же поля или ее центр и одна ее точка имеют координаты в поле Q(a, b, с, . ), то уравне­ние самой окружности будет иметь коэффициенты в том же поле. Однако для определения координат точек пересечения двух таких окружностей или прямой и окружности требуется привлечение квадратных корней.

Отсюда следует, что если какую-нибудь точку можно построить с помощью циркуля и линейки, то ее координаты должны получаться из поля Q(a, b, с, . ) по формуле, содержащей лишь квадратные корни. Иными словами, координаты такой точки должны лежать в некотором поле вида , где каждое поле явля­ется полем разложения некоторого квадратного многочлена х 2 — над полем .

Отсюда следует, что ( / ) является сте­пенью числа 2, поскольку либо

= либо ( ) = 2. Если х — координата построенной точки, то

Обратно, если координаты какой-нибудь точки можно получить из Q(a,b,с, . ) по формуле, использующей только квадратные корни, то такую точку можно построить с помощью циркуля и линейки. Действи­тельно, с помощью циркуля и линейки можно выполнить сложение, вы­читание, умножение и деление, а если использовать равенство 1 : r = r : r₁, то можно осуществить и извлечение квадратного корня r = .

В качестве иллюстрации этих рассуждений докажем, что трисекция угла в 60° невозможна. Предположим, что мы провели окружность еди­ничного радиуса с центром в вершине угла. Введем координатную систе­му таким образом, чтобы ось абсцисс совпадала с одной из сторон угла, а начало координат совпадало с вершиной угла.

Трисекция угла была бы эквивалентна построению точки с коор­динатами (cos20°, sin20°) на единичной окружности. Из уравнения cos =4cos 3 —3cos следует, что абсцисса такой точки удовлетво­ряет уравнению 4х 3 — Зх= 1/2. Можно легко проверить, что у этого уравнения нет рациональных корней, поэтому оно неприводимо над полем рациональных чисел. Но поскольку мы предположили, что нам даны только прямая и отрезок единичной длины, и поскольку построение угла в 60° возможно, то поле

Q(a, b, с, . ) можно считать изоморфным полю Q рациональных чисел. Однако корень неприводимого уравнения 8x 3 — 6x — 1=0 обладает тем свойством, что (Q( )/Q) = 3, и степень этого расширения не является степенью двойки.

Видео:ЛЕКЦИЯ №4 - КОНЕЧНЫЕ ПОЛЯСкачать

3.3 Вычисление группы Галуа

Один из методов, с помощью которого можно построить группу Галуа уравнения f(x) = 0 над полем A, состоит в следующем [20].

Пусть , . — корни уравнения. Построим с помощью переменных выражение

применим к нему всевозможные подстановки s_u переменных и составим произведение

Очевидно, это произведение является симметрической функцией корней и поэтому, может быть выражено через коэффициенты многочлена f(x). Разложим многочлен F(z, и) на неразложимые множители в кольце A [и z]:

Теорема 13. Постановки , которые переводят в себя некоторый сомножитель, скажем, сомножитель F₁ составляют группу ɡ. Мы утверждаем, что группа ɡ —это в точности группа Галуа заданного уравнения.

Доказательство. После присоединения всех корней многочлен F, а потому и многочлен F₁ разлагаются на линейные множители вида z —∑ u_vα_v, коэффициентами которых служат корни α_v, расположенные в некотором порядке. Перенумеруем корни так, чтобы F₁ содержал множитель

. В последующем символ s_u будет обозначать подстановку симво­лов и, а s_α — такую же подстановку символов α . Очевидно, что в таких обо­значениях подстановка s_us_α оставляет выражение θ = . инвариантным, т. е.

Если подстановка s_u принадлежит группе ɡ, т. е. оставляет инвариантным многочлен F₁ , то s_u переводит каждый множитель многочлена F₁ в частности z-θ, вновь в некоторый линейный множитель многочлена F₁ . Обратно, если некоторая подстановка s_u переводит множитель z-θ в другой линейный мно­житель многочлена F₁, то она переводит F₁ в некоторый неразложимый в кольце A[и,z] многочлен, являющийся делителем многочлена F (z, и), т. е. в один из многочленов Fj и притом в такой, у которого есть общий линей­ный множитель с F₁; это означает, что F₁, переводится в себя. Следовательно, подстановка s_u принадлежит группе ɡ. Таким образом, группа ɡ состоит из подстановок символов и, которые переводят z— θ в линейный множитель мно­гочлена F₁.

Подстановки s_α из группы Галуа многочлена f(x) — это такие подстановки символов α, которые переводят выражение

в сопряженные с ним и для которых, следовательно, элемент s_αθ удовлетво­ряет тому же неразложимому уравнению, что и θ, т. е. это такие подста­новки s_α , которые переводят линейный множитель z— θ в другой линейный множитель многочлена F₁ . Так как s_αθ = θ, то подстановка также пере­водит линейный множитель z-θ в линейный множитель многочлена F₁ т. е. , а потому и s_u, принадлежит группе ɡ. Верно и обратное утверждение. Следовательно, группа Галуа состоит из тех и только тех подстановок, кото­рые входят в группу ɡ, нужно только символы α заменить на символы и.

Этот метод определения группы Галуа интересен не столько практически, сколько теоретически; из него получается чисто теоретическое следствие, кото­рое звучит так:

Пусть ß — целостное кольцо с единицей, в котором имеет место теорема об однозначном разложении на простые множители. Пусть ν — простой идеал в ß и = ß/p —кольцо классов вычетов. Пусть A и — поля частных колец ß и . Наконец, пусть f (х) = +… — многочлен из ß [х], a (x) получается из f(х) при гомоморфизме ß → , причем оба многочлена не имеют кратных корней. Тогда группа уравнения = 0 над полем (как группа подстановок подходящим образом перенумерованных корней) является подгруппой группы g уравнения f = 0.

Доказательство Разложение многочлена

Множители ₁ возможно, окажутся разложимыми дальше. Подстановки из группы переводят F₁, а потому и ₁ в себя, а остальные подста­новки символов и переводят ₁ в ₂,…, _k .

Теорема 14. Подстановки из группы пере­водят любой неразложимый множитель многочлена ₁ в себя; поэтому они не могут переводить ₁ в ₂,…, _k : обязательно ₁ переводится в себя, т. е. — некоторая подгруппа группы .

Эта теорема часто используется для нахождения группы . При этом идеал ν выбирают так, чтобы многочлен f(х) был разложим по модулю ν, потому что тогда легче определить группу уравнения . Пусть, например, β — кольцо целых чисел и ν = (р), где р — простое число. Тогда по модулю р многочлен f(х) представляется в виде

Группа многочлена (х) циклична, так как группа автоморфизмов поля Галуа обязательно циклична. Пусть s — подстановка, порождающая группу и представляющаяся в виде циклов следующим образом:

Так как области транзитивности группы соответствуют неразложимым мно­жителям многочлена f, то символы, входящие в циклы (1 2 . j)(. ). должны находиться в точном соответствии с корнями многочленов ₁ , ₂. Как только оказываются известными степенями j, k, . многочленов s, оказывается известным и тип подстановки: подстановка состоит тогда из одного j-членного цикла, одного k — членного цикла и т. д. Так как в соответствии с приведенной выше теоремой при подходящей нумерации корней группа оказывается подгруппой группы , группа должна содержать подстановку такого же типа.

Так, например, если целочисленные уравнения пятой степени по модулю какого-либо простого числа распадается в произведение неразложимого множителя второй степени и неразложимого множителя третьей степени, то группа Галуа обязана содержать подстановку типа (1 2) (3 4 5) [18].

Пример1. Пусть дано целочисленное уравнение

Решение: По модулю 2 левая часть разлагается в произведение

а по модулю 3 она неразложима, потому что иначе у нее был бы множитель первой или второй степени, а потому и общий множитель с х 9 — х; последнее означает наличие общего множителя либо с х 5 — х, либо с х 5 — х, что, очевидно, невозможно. Тем самым группа заданного уравнения содержит один пятичленный цикл и произведение (i k) (l т п). Третья степень последней подстановки равна (i k), а эта последняя, трансформированная с помощью подстановки (1 2 3 4 5) и ее степеней, дает цепь транспозиций

С помощью установленных фактов можно построить уравнение произволь­ной степени с симметрической группой; основанием служит следующая теорема:

Теорема 15. Транзитивная группа подстановок n-й степени, содержащая один двойной цикл и один (n —1) — членный цикл, является симметрической.

Доказательство. Пусть (1 2 . п— 1) — данный (п — 1)-членный цикл. Двойной цикл (i j) в силу транзитивности можно перевести в цикл (k n), где k—один из символов от 1 до п—1. Трансформирование цикла (k п) с помощью цикла (1 2 . n— 1) и степеней последнего дает циклы

Чтобы на основании этой теоремы построить уравнение п-й степени (п>3) с симметрической группой, выберем сначала неразложимый по модулю 2 многочлен n-й степени f₁, а затем многочлен f₂, который по модулю 3 разлагается в произведение неразложимого многочлена (n—1)-й степени и линейного мно­гочлена, и, наконец, выберем многочлен f₃ степени п, который по модулю 5 разлагается в произведение квадратного множителя и одного или двух множи­телей нечетных степеней (все они должны быть неразложимыми по модулю 5). Все это возможно, потому что по модулю любого простого числа существует неразложимый многочлен любой наперед заданной степени [7].

В заключение выберем многочлен f так, чтобы выполнялись условия:

сделать это всегда возможно. Достаточно, например, положить

Группа Галуа будет тогда транзитивной (так как многочлен неразложим по модулю 2) и будет содержать цикл типа (1 2 . n — 1) и двойной цикл, умно­женный на циклы нечетного порядка. Если это последнее произведение воз­вести в нечетную степень, подходящим образом подобранную, то получится чистый двойной цикл. Согласно приведенной выше теореме группа Галуа будет симметрической.

С помощью этого метода можно доказать не только существование уравне­ний с симметрической группой Галуа, но и нечто большее: именно, асимпто­тически все целочисленные уравнения, коэффициенты которых не превосходят границу N, стремящуюся к , имеют симметрическую группу.

Заключение

Изучение элементов теории поля полезно для студентов, способствует их интеллектуальному росту, проявляющемуся в развитии и обогащении различных сторон их мышления, качеств и черт личности, а также воспитанию у учащихся интереса к математике, к науке.

Целью дипломной работы было изучение теории Галуа и ее приложений. Для достижения поставленной цели были решены следующие задачи: получены первые сведения о строении полей, об их простейших подполях и расширениях, а так же рассмотрены группы Галуа и основная теорема Галуа.

В работе были самостоятельно решены задачи по теории Галуа. Так же были приведены интересные примеры по соответствующим теоретическим сведениям.

Список литературы

1. Артин Э. Теория Галуа / Пер. с англ. Самохина А. В. – М.: МЦНМО, 2004, 66с.
2. Бурбаки Н.. Алгебра. Многочлены и поля. Упорядоченные группы. М.:Наука, 1965.
3. Ван дер Варден (van der Waerden В. ). — Math, Ann., 1931, 109, S 13.
4. Винберг Э. Б. Курс алгебры 2-е издание