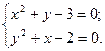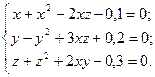Решение уравнений в матлабе fzero (7 видео)

Решение уравнений и их систем

Дата добавления: 2015-06-12 ; просмотров: 2950 ; Нарушение авторских прав

Команда fzero вычисляет вещественный корень уравнения f(x)=0.

Команда fzero имеет следующие модификации:

fzero(‘f(x)’, x0);

fzero(‘f(x)’, [x1, x2]).,kk

В выражениях функции приняты следующие обозначения:

‘f(x)’ – решаемое уравнение или имя файл-функции (в одинарных кавычках), вычисляющей левую часть уравнения;

x0 – начальное приближение (значение) искомого корня;

[x1, x2] – область изоляции корня.

Команда fzero имеет и другие модификации, о которых можно узнать с помощью команды doc fzero.

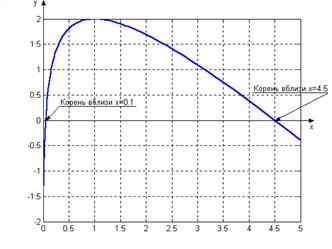
Вычислить корни уравнения lnx — x+3 = 0 на отрезке [0;5].

Создадим файл-функцию myfun, вычисляющую значение функции lnx — x+3 при заданном значении аргумента x:

Перед нахождением корней построим график исследуемой функции командой fplot и нанесем сетку (рис. 6.1):

Пояснения на графике нанесены средствами MATLAB. На графике видно, что функция на этом отрезке имеет два корня, расположенные вблизи 0,1 и 4,5. Уточним значение второго корня при помощи fzero:

Итак, приближенное значение второго корня равно х₂ = 4,5052. Вместо начального приближения 4,5 вторым параметром fzero можно задать интервал [4;5], на котором следует найти корень:

Отметим, что на границах указываемого интервала функция должна принимать значения разных знаков, иначе выдается сообщение об ошибке.

Получить приближенное значение корня и значение функции в этой точке позволяет вызов fzero с двумя выходными аргументами:

То, что значение функции близко к нулю, вообще говоря, не означает, что приближенное значение корня расположено достаточно близко к его точному значению.

Для того, чтобы увидеть больше значащих цифр корня х₂, установим формат long и выведем х₂ еще раз (точность вычислений не зависит от формата вывода результата):

Найдем корень х₁, расположенный около 0,1:

Возникает вопрос, сколько в ответе точных значащих цифр, т. е. с какой точностью найдено решение? Задание точности вычислений обсуждается ниже в разделах 6.4, 6.5.

Важной особенностью fzero является то, что она вычисляет только те корни, в которых функция меняет знак, а не касается оси абсцисс. Найти корень уравнения x 2 = 0 при помощи fzero нельзя (получим сообщение об ошибке).

Многомерным аналогом fzero является команда fsolve, предназначенная для решения системы нелинейных уравнений F(X) = 0. Одна из модификаций fsolve имеет вид fsolve(‘file’, x0). Здесь

file – имя файл-функции, вычисляющей вектор-столбец левых частей системы уравнений,

x0 – вектор-столбец начальных приближений.

Первый входной аргумент можно задать как указатель на файл-функцию @»file.

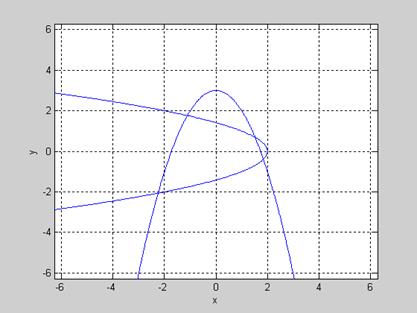
Решить cистему нелинейных уравнений

1) имеет ли система вещественные решения?;

2) если вещественные решения есть, то как определить их начальные приближения?

Т. к. система имеет второй порядок, то ответ на эти вопросы легко найти графическим способом. С помощью команды ezplot (см. разд. 7.16), cтроим совместно графики парабол x 2 +y=3 и y 2 +x=2 на рис. 6.2:

Current plot held

Как видно на рис. 6.2 система имеет 4 вещественных решения (количество точек пересечения графиков), а одно из них имеет начальное приближение (-1;2). Уточним его с помощью команды fsolve.

Создадим файл-функцию mfun2, вычисляющую вектор-столбец левых частей системы уравнений:

Программа и результаты решения системы уравнений имеют вид:

Получить одновременно приближенное решение и значения левых частей системы уравнений (функций x 2 +y — 3 и y 2 +x — 2) при подстановке в них этого решения позволяет вызов fsolve с двумя выходными аргументами:

Таким образом, (x;y)=(-1,1117;1,7640) – одно из приближенных вещественных решений системы. Изменяя стартовые значения (согласно рис. 6.2), можно найти и остальные вещественные решения.

Решить cистему уравнений третьего порядка

Для такой системы нельзя найти области начальных приближений графическим способом. Создадим файл-функцию mfun3, вычисляющую вектор-столбец левых частей системы уравнений:

Для произвольного стартового значения решения (-1;0;0) программа и результаты решения системы уравнений имеют вид:

Итак, (x;y;z)=(-1,0880; -0,1303; 0,0161) – одно из приближенных вещественных решений системы. Изменяя стартовые значения, можно попытаться найти и другие вещественные решения этой системы.

Команда fsolve имеет и другие модификации, о которых можно узнать с помощью команды doc fsolve.

Команда fsolve также применима для решения одного нелинейного уравнения. В этом случае ее первый аргумент задает скалярную функцию, а вектор x0 – совокупность начальных приближений. Например:

0 3.1416 6.2832 9.4248 12.5664

дает совокупность решений уравнения sin(x) = 0, наиболее близких к соответственным стартовым точкам массива х0.

При решении используется оптимизационный алгоритм, осуществляющий минимизацию невязки F(X). Поэтому команда fsolve способна найти нули, в том числе и таких функций, как x 2 и .

Существенный недостаток команд fzero и fsolve состоит в том, что они не определяют комплексных решений уравнений и систем уравнений. Команда solve пакета Symbolic дополняет эти команды. С ее помощью в разделе 7.13 будут найдены другие решения рассмотренных выше систем уравнений, в том числе и комплексные.

\|	следующая лекция ==>
\|	Минимизация функции одной переменной

Не нашли то, что искали? Google вам в помощь!

Содержание

fzero
Syntax
Description
Examples
Root Starting From One Point
Root Starting From an Interval
Root of a Function Defined by a File
Root of Function with Extra Parameter
Nondefault Options
Solve Problem Structure
More Information from Solution
Input Arguments
fun — Function to solve function handle | function name
x0 — Initial value scalar | 2-element vector
Решение уравнений в матлабе fzero
🎦 Видео

Видео:2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

fzero

Root of nonlinear function

Видео:MATLAB Video 17: fzero functionСкачать

Syntax

Видео:1 - Решение систем нелинейных уравнений в MatlabСкачать

Description

x = fzero( fun , x0 ) tries to find a point x where fun(x) = 0 . This solution is where fun(x) changes sign— fzero cannot find a root of a function such as x^2 .

x = fzero( fun , x0 , options ) uses options to modify the solution process.

x = fzero( problem ) solves a root-finding problem specified by problem .

[ x , fval , exitflag , output ] = fzero( ___ ) returns fun(x) in the fval output, exitflag encoding the reason fzero stopped, and an output structure containing information on the solution process.

Видео:Методы вычислений в MATLAB. Исследование функций, встраиваемые и анонимные функции. Урок 60Скачать

Examples

Root Starting From One Point

Calculate π by finding the zero of the sine function near 3 .

Root Starting From an Interval

Find the zero of cosine between 1 and 2 .

Note that cos ( 1 ) and cos ( 2 ) differ in sign.

Root of a Function Defined by a File

Find a zero of the function f( x) = x 3 – 2 x – 5.

First, write a file called f.m .

Save f.m on your MATLAB ® path.

Find the zero of f( x) near 2 .

Since f(x) is a polynomial, you can find the same real zero, and a complex conjugate pair of zeros, using the roots command.

Root of Function with Extra Parameter

Find the root of a function that has an extra parameter.

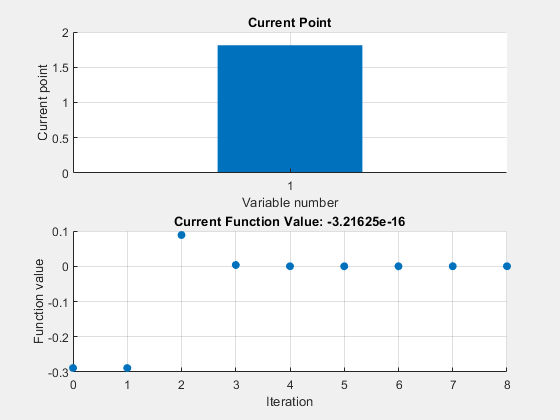
Nondefault Options

Plot the solution process by setting some plot functions.

Define the function and initial point.

Examine the solution process by setting options that include plot functions.

Run fzero including options .

Solve Problem Structure

Solve a problem that is defined by a problem structure.

Define a structure that encodes a root-finding problem.

Solve the problem.

Input Arguments

fun — Function to solve
function handle | function name

Function to solve, specified as a handle to a scalar-valued function or the name of such a function. fun accepts a scalar x and returns a scalar fun(x) .

fzero solves fun(x) = 0 . To solve an equation fun(x) = c(x) , instead solve fun2(x) = fun(x) — c(x) = 0 .

To include extra parameters in your function, see the example Root of Function with Extra Parameter and the section Parameterizing Functions.

Example: ‘sin’

Example: @myFunction

Example: @(x)(x-a)^5 — 3*x + a — 1

Data Types: char | function_handle | string

x0 — Initial value
scalar | 2-element vector

Initial value, specified as a real scalar or a 2-element real vector.

Scalar — fzero begins at x0 and tries to locate a point x1 where fun(x1) has the opposite sign of fun(x0) . Then fzero iteratively shrinks the interval where fun changes sign to reach a solution.

2-element vector — fzero checks that fun(x0(1)) and fun(x0(2)) have opposite signs, and errors if they do not. It then iteratively shrinks the interval where fun changes sign to reach a solution. An interval x0 must be finite; it cannot contain ± Inf .

Tip

Calling fzero with an interval ( x0 with two elements) is often faster than calling it with a scalar x0 .

Видео:Решение системы уравнений Колмогорова в МатлабеСкачать

Решение уравнений в матлабе fzero

Find zero of a function of one variable

x = fzero(fun,x0) tries to find a zero of fun near x0 , if x0 is a scalar . fun is a function handle. See Function Handles in the MATLAB Programming documentation for more information. The value x returned by fzero is near a point where fun changes sign, or NaN if the search fails. In this case, the search terminates when the search interval is expanded until an Inf , NaN , or complex value is found.

Parameterizing Functions Called by Function Functions, in the MATLAB mathematics documentation, explains how to provide additional parameters to the function fun , if necessary.

If x0 is a vector of length two, fzero assumes x0 is an interval where the sign of fun(x0(1)) differs from the sign of fun(x0(2)) . An error occurs if this is not true. Calling fzero with such an interval guarantees fzero will return a value near a point where fun changes sign.

x = fzero(fun,x0,options) minimizes with the optimization parameters specified in the structure options . You can define these parameters using the optimset function. fzero uses these options structure fields:

Display	Level of display. ‘off’ displays no output; ‘iter’ displays output at each iteration; ‘final’ displays just the final output; ‘notify’ (default) displays output only if the function does not converge.
FunValCheck	Check whether objective function values are valid. ‘on’ displays a warning when the objective function returns a value that is complex or NaN . ‘off’ (the default) displays no warning.
OutputFcn	Specify a user-defined function that the optimization function calls at each iteration.
TolX	Termination tolerance on x

[x,fval] = fzero(. ) returns the value of the objective function fun at the solution x .

[x,fval,exitflag] = fzero(. ) returns a value exitflag that describes the exit condition of fzero :

1	Function converged to a solution x .
-1	Algorithm was terminated by the output function.
-3	NaN or Inf function value was encountered during search for an interval containing a sign change.
-4	Complex function value was encountered during search for an interval containing a sign change.
-5	fzero might have converged to a singular point.

[x,fval,exitflag,output] = fzero(. ) returns a structure output that contains information about the optimization:

output.algorithm	Algorithm used
output.funcCount	Number of function evaluations
output.intervaliterations	Number of iterations taken to find an interval
output.iterations	Number of zero-finding iterations
output.message	Exit message

Note For the purposes of this command, zeros are considered to be points where the function actually crosses, not just touches, the x-axis.

fun is the function whose zero is to be computed. It accepts a vector x and returns a scalar f , the objective function evaluated at x . The function fun can be specified as a function handle for an M-file function

where myfun is an M-file function such as

or as a function handle for an anonymous function:

Other arguments are described in the syntax descriptions above.

Example 1. Calculate by finding the zero of the sine function near 3.

Example 2. To find the zero of cosine between 1 and 2

Note that cos(1) and cos(2) differ in sign.

Example 3. To find a zero of the function

write an anonymous function f :

Then find the zero near 2:

Because this function is a polynomial, the statement roots([1 0 -2 -5]) finds the same real zero, and a complex conjugate pair of zeros.

If fun is parameterized, you can use anonymous functions to capture the problem-dependent parameters. For example, suppose you want to minimize the objective function myfun defined by the following M-file function.

Note that myfun has an extra parameter a , so you cannot pass it directly to fzero . To optimize for a specific value of a , such as a = 2 .

Assign the value to a .
Call fzero with a one-argument anonymous function that captures that value of a and calls myfun with two arguments:

The fzero command is an M-file. The algorithm, which was originated by T. Dekker, uses a combination of bisection, secant, and inverse quadratic interpolation methods. An Algol 60 version, with some improvements, is given in [1]. A Fortran version, upon which the fzero M-file is based, is in [2].

The fzero command finds a point where the function changes sign. If the function is continuous, this is also a point where the function has a value near zero. If the function is not continuous, fzero may return values that are discontinuous points instead of zeros. For example, fzero(@tan,1) returns 1.5708 , a discontinuous point in tan .

Furthermore, the fzero command defines a zero as a point where the function crosses the x-axis. Points where the function touches, but does not cross, the x-axis are not valid zeros. For example, y = x.^2 is a parabola that touches the x-axis at 0. Because the function never crosses the x-axis, however, no zero is found. For functions with no valid zeros, fzero executes until Inf , NaN , or a complex value is detected.

[1] Brent, R., Algorithms for Minimization Without Derivatives, Prentice-Hall, 1973.

[2] Forsythe, G. E., M. A. Malcolm, and C. B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1976.