Решение уравнений в кольце вычетов онлайн калькулятор

Обратный по модулю

Калькулятор онлайн для вычисления обратного элемента по модулю в кольце. Алгоритм поддерживает работу с большими числами с некоторыми ограничениями.

Использование:

Заполняются два поля — число a и модуль m. Число a — число к которому ищем обратный, m — модуль, по которому ищем.

Калькулятор выдает обратный элемент после нажатия на кнопку «Вычислить».

Если установлена галочка «подробнее», то калькулятор помимо обратного элемента по модулю выдает некоторые этапы вычисления.

Ограничения:

Калькулятор поддерживает работу с большими целыми числами (в том числе отрицательными числами для числа a, и только положительными для модулю m) длиной не более 10 000 символов.

Что значит по модулю?

Синонимом к данному выражению является выражение «остаток от деления«. То есть выражение «5 по модулю 3» эквивалентно выражению «остаток от деления 5 на 3». И в том и в другом случае подразумевается в ответе число 2, так как остаток от деления 5 на 3 = 2.

Стоить отметить тот факт, что по модулю m мы имеем числа от 0 до m — 1. Действительно, остаток от деления на m никогда не превысит m — 1.

Что такое обратное?

Напомним, что число, умноженное на его обратное, равно 1. Из базовой арифметики мы знаем, что:

Число, обратное к числу A, равно 1 / A, поскольку A * (1 / A) = 1 (например, значение, обратное к 5, равно 1/5).
Все действительные числа, кроме 0, имеют обратную
Умножение числа на обратное к A эквивалентно делению на A (например, 10/5 соответствует 10 * 1/5)

Что такое обратное по модулю?

В модульной арифметике у нас нет операции деления. Тем не менее, у нас есть модульные инверсии.

Модульная инверсия a (mod m) есть a -1
(a * a -1 ) ≡ 1 (mod m) или эквивалентно (a * a -1 ) mod m = 1
Только числа, взаимно простые с модулем m, имеют модульное обратное.

Говоря проще, обратным элементом к a по модулю m является такое число b, что остаток от деления (a * b) на модуль m равно единице (a * a -1 ) mod m = 1

Как найти модульный обратный

Наивный метод нахождения модульного обратного a ( по модулю m) является:
Шаг 1. Рассчитать a * b mod m для значений b от 0 до m — 1
Шаг 2. Модульная инверсия a mod m — это значение b, при котором a * b mod m = 1

Обратите внимание, что термин b mod m может иметь только целочисленное значение от 0 до m — 1, поэтому тестирование больших значений чем (m-1) для b является излишним.

Вы наверно уже догадались, что наивный метод является очень медленным. Перебор всех чисел от 0 до m-1 для большого модуля довольно-таки трудоемкая задача. Существует гораздо более быстрый метод нахождения инверсии a (mod m). Таковым является расширенный алгоритм Евклида, который реализован в данном калькуляторе.

Расширенный алгоритм Евклида

Представим наибольший общий делитель числа a и модуля m в виде ax + my. То есть НОД(a, m) = ax + my. Помним, что обратный элемент существует только тогда, когда a и m взаимно просты, то есть их НОД(a, m) = 1. Отсюда: ax + my = 1 — линейное диофантово уравнение второго порядка. Необходимо решить данное уравнение в целых числах и найти x, y.

Найденный коэффициент x будет являться обратным элементом к a по модулю m. Это следует оттуда, что, если мы возьмём от обеих частей уравнения остаток по модулю m, то получим: ax = 1 (m).

Расширенный алгоритм Евклида, в отличие от классического, помимо наибольшего общего делителя позволяет найти также коэффициенты x, y.

Алгоритм:

Выход : d, x, y, такие что d = gcd(a, m) = ax + my

3. [Выход] Вернуть (d, x, y) = (a₀, x₀, y₀)

Битовая сложность расширенного алгоритма Евклида равна O((log₂(n)) 2 ) , где n = max (|a|, |m|)

Непонятен алгоритм? Ничего страшного, примеры ниже именно для этого и предназначены.

Пример для наивного метода.

Пусть a = 3, m = 7. То есть нам необходимо найти обратный элемент к 3 по модулю 7.

Шаг 1 . Рассчитать a * b mod m для значений B от 0 до m-1. По очереди проверяем числа от 0 до 6.

3 * 0 ≡ 0 (mod 7) — не подходит
3 * 1 ≡ 3 (mod 7)
3 * 2 ≡ 6 (mod 7)
3 * 3 ≡ 9 ≡ 2 (mod 7)
3 * 4 ≡ 12 ≡ 5 (mod 7)
3 * 5 ≡ 15 (mod 7) ≡ 1 (mod 7) Пример на расширенный алгоритм Евклида.

Пусть аналогично предыдущему примеру имеем a = 3, m = 7. Также, требуется найти обратный элемент к 3 по модулю 7. Согласно алгоритму начинаем заполнять таблицу на каждом этапе цикла.

После 3-ей итерации получили a1 = 0, строго по алгоритму из раздела «Теория» заканчиваем работу алгоритма.

(d, x, y) = (1, -2, 1), видим, что d = НОД(3, 7) = 1, следовательно числа 3 и 7 являются взаимно простыми, а значит обратный существует.

Делаем проверку:

3 * (-2) + 7 * 1 = 1
-6 + 7 = 1
1 = 1 — верно!

Обратным элементом к тройке по модулю 7 является x = -2. По модулю 7 число -2 равно 5. Получили, что x = 5 является обратным элементом к 3 по модулю 7.

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Решение уравнений в кольце остатков по данному модулю

Дата добавления: 2015-07-23 ; просмотров: 3966 ; Нарушение авторских прав

Сравнение 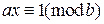всегда имеет решение, если числа a и b взаимно просты.

Это следует из того, что выражение ax-by = 1 – это линейное представление наибольшего общего делителя a и b.

Такую задачу иногда формулируют в виде: найти 1/a в кольце вычетов по модулю b. В самом деле, выражение ax = 1 означает по сути то же самое, что x = 1/a (x – искомая величина).

В некоторых случаях вычисляют c/a в кольце вычетов по модулю b. В этом случае сначала можно вычислить 1/a, затем умножить результат на c в кольце вычетов по модулю b.

Уточняем, что умножить число в кольце вычетов по модулю b означает сначала умножить число, затем заменить результат его остатком от деления на b.

Можно решить уравнение 7x = 1 в кольце вычетов по модулю 9, то есть провести вычисление 1/7 в Z₉.

В данном случае обозначим неизвестную величину как х.

Тогда x = 1/7 в Z₉ Û

7x – 1 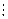9 Û

Мы получили уже знакомую нам ситуацию – линейное диофантово уравнение.

Можем его решить, но для первоначальной задачи достаточно найти всего одно значение х – например, подойдёт x = 4. Заметим, что это число находится в пределах от 0 до 8, поэтому может быть остатком при делении на 9.

Итак, ответ: x = 4.

Примечание. Ответ легко проверить умножением: 4 х 7 при делении на 9 даёт остаток 1.

Если бы мы искали, например, 5/7 в Z₉, то сначала нашли бы сначала 1/7 в Z₉ (получив число 4), а затем домножили бы это число на 5 и взяли бы остаток при делении на 9 (остаток от деления 20 на 9 равен 2).

В этом случае ответ был бы равен 2.

Примечание. В задачах на нахождение выражений вида a/b в кольце вычетов по модулю c ответ всегда единственный, и является целым числом, находящимся в пределах от 0 до (c — 1).

В некоторых случаях деление невозможно, поскольку не каждое диофантово уравнение имеет решение. Например, уравнение 4x º 1 (mod 10) не имеет решений, поскольку 4x – чётное число, и при делении на 10 остаток будет чётным.

Не нашли то, что искали? Google вам в помощь!

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Обратный элемент в кольце по модулю

Калькулятор вычисляет обратный элемент по модулю.

Калькулятор для вычисления обратного элемента по модулю ниже, теория под ним.

Обратный элемент в кольце по модулю

Обратным к числу a по модулю m называется такое число b, что:
,
Обратный элемент обозначают как .

Для нуля обратного элемента не существует никогда, для остальных же элементов обратный элемент может как существовать, так и нет.
Утверждается, что обратный элемент существует только для тех элементов a, которые взаимно просты с модулем m.

Для нахождения обратного элемента по модулю можно использовать Расширенный алгоритм Евклида.

Для того, чтобы показать это, рассмотрим следующее уравнение:

Это линейное диофантово уравнение с двумя переменными, см. Линейные диофантовы уравнения с двумя переменными. Посколько единица может делиться только на единицу, то уравнение имеет решение только если .
Решение можно найти с помощью расширенного алгоритма Евклида. При этом, если мы возьмём от обеих частей уравнения остаток по модулю m, то получим:

Таким образом, найденное x и будет являться обратным к a.

🔥 Видео

Решение уравнений на множестве Q. -6 классСкачать

Показательные уравнения. 11 класс.Скачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Составление уравнений химических реакций. 1 часть. 8 класс.Скачать

КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать

Математика 2 класс (Урок№26 - Уравнение. Решение уравнений подбором неизвестного числа.)Скачать

Алгебраические уравнения в кольце вычетовСкачать

Решение задач на термохимические уравнения. 8 класс.Скачать

Уравнение. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Как посчитать любое уравнение! Шок!!Скачать

Решение уравнений. Видеоурок 28. Математика 6 классСкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

КАК СПИСАТЬ СЛОЖНЫЕ УРАВНЕНИЯ ПО МАТЕМАТИКЕ, ЕСЛИ ИХ НЕТ В ИНТЕРНЕТЕ? #shortsСкачать

Решение уравнений, 6 классСкачать