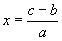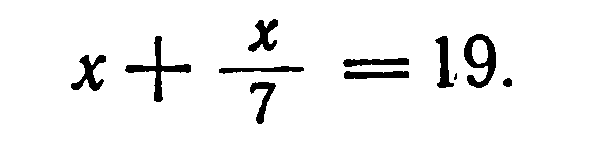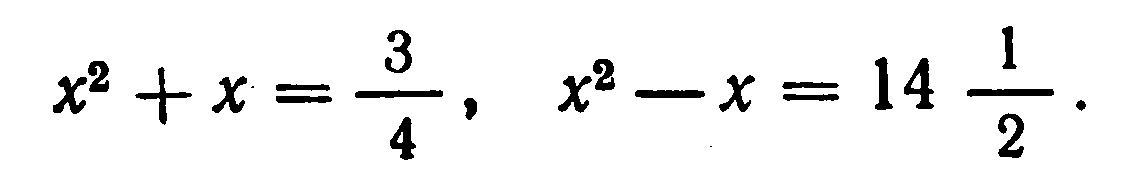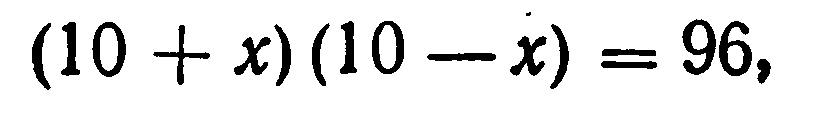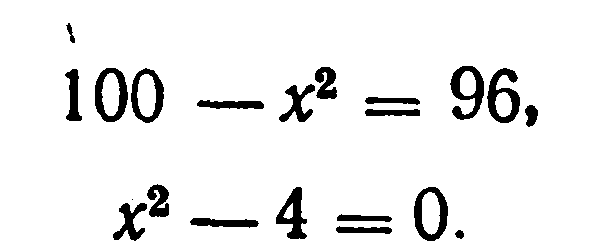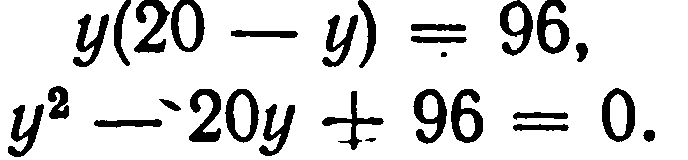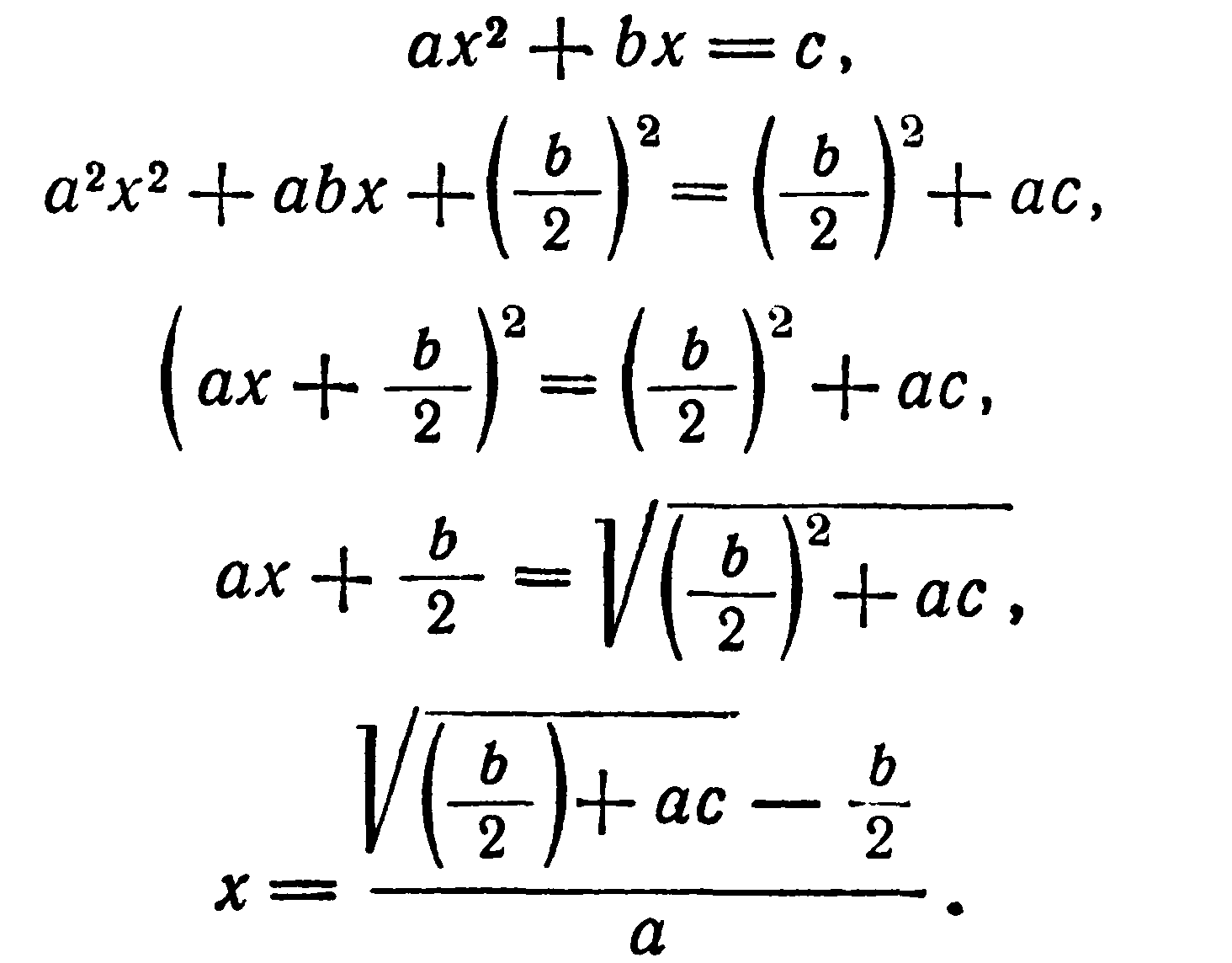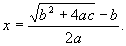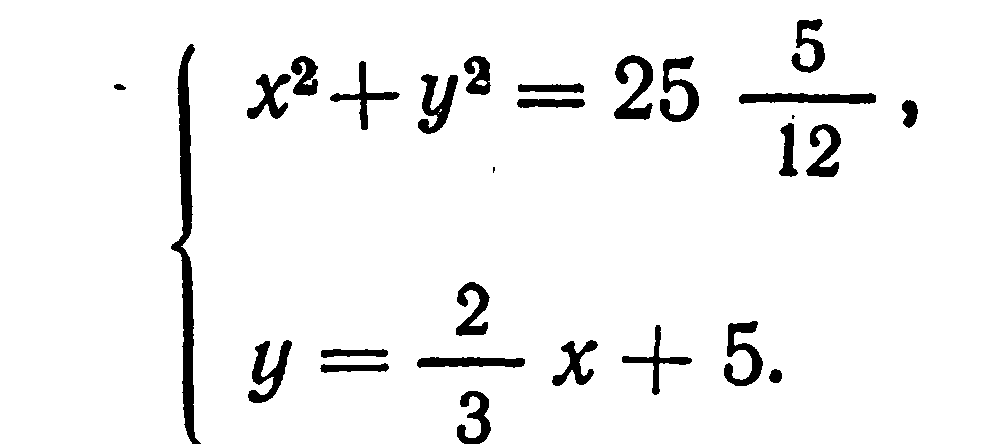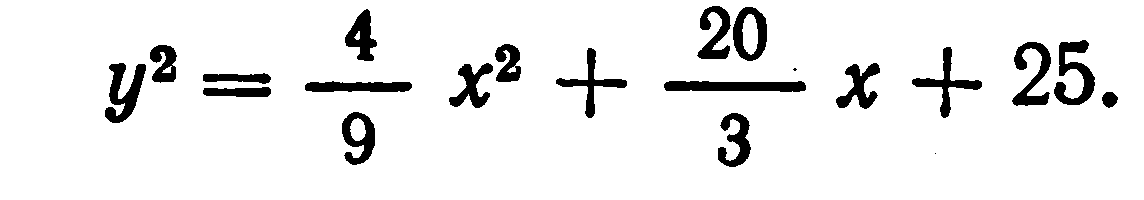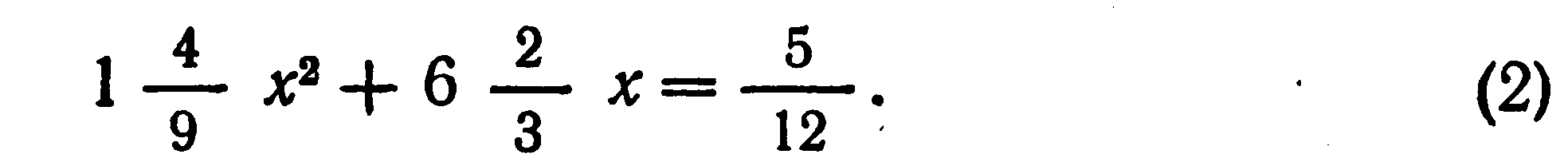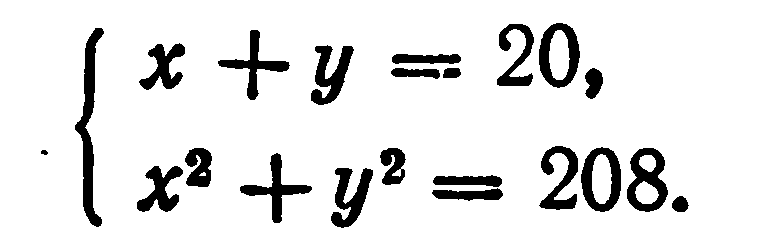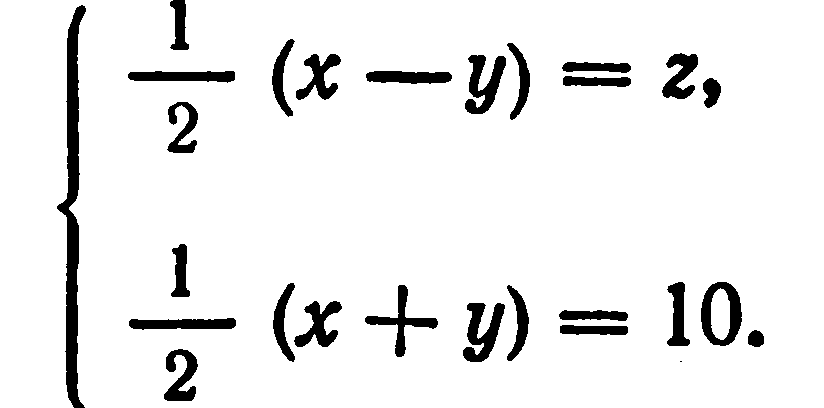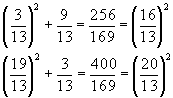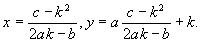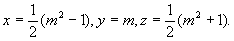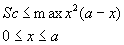Решение уравнений в древнем вавилоне (4 видео)

Из истории возникновения квадратных уравнений

Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.

Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.

Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

Задача 2. «Найти два числа, зная, что их сумма равна 20, а произведение — 96».

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х. Другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение:

Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = — 2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если решить эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то можно прийти к решению уравнения:

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.

Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Вот одна из задач знаменитого индийского математика XII в. Бхаскары.

«Обезьянок резвых стая

А двенадцать по лианам

Всласть поевши, развлекалась

Стали прыгать, повисая

Их в квадрате часть восьмая

Сколько ж было обезьянок,

На поляне забавлялась

Ты скажи мне, в этой стае?»

Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений.

Соответствующее задаче 3 уравнение:

Бхаскара пишет под видом:

x2 — 64x = — 768

и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем:

x2 — б4х + 322 = -768 + 1024,

Квадратные уравнения у Аль-Хорезми

В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т. е. ах2 = bх.

2) «Квадраты равны числу», т. е. ах2 = с.

3) «Корни равны числу», т. е. ах = с.

4) «Квадраты и числа равны корням», т. е. ах2 + с = bх.

5) «Квадраты и корни равны числу», т. е. ах2 + bх =с.

6) «Корни и числа равны квадратам», т. е. bх + с == ах2.

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Задача 4. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х2 + 21 = 10х).

Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.

Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.[3,75]

Квадратные уравнения в Европе XII—XVII в.

Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.

Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.[5,12].

Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX—VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.

Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI—Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака. А затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры, использование букв, введение символов арифметических операций, скобок и т. д. На рубеже XVI—XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики.

Итак, ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования.

Для того чтобы решить любое квадратное уравнение, надо знать:

· формулу нахождения дискриминанта;

· формулу нахождения корней квадратного уравнения;

· алгоритмы решения уравнений данного вида.

· решать неполные квадратные уравнения;

· решать полные квадратные уравнения;

· решать приведенные квадратные уравнения;

· находить ошибки в решенных уравнениях и исправлять их;

Решение каждого уравнения складывается из двух основных частей:

· преобразования данного уравнения к простейшим;

· решения уравнений по известным правилам, формулам или алгоритмам.

Обобщение способов деятельности учащихся при решении квадратных уравнений происходит постепенно. Можно выделить следующие этапы при изучении темы «Квадратные уравнения»:

I этап – «Решение неполных квадратных уравнений».

II этап – «Решение полных квадратных уравнений».

III этап – «Решение приведенных квадратных уравнений».

На первом этапе рассматриваются неполные квадратные уравнения. Так как сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать. Это уравнения вида: ах2 = 0, ах2 + с = 0, где с≠ 0, ах2 + bх = 0, где b ≠ 0. Рассмотрим решение несколько таких уравнений:

1. Если ах2 = 0. Уравнения такого вида решаются по алгоритму:

Например, 5х2 = 0 . Разделив обе части уравнения на 5 получается: х2 = 0, откуда х = 0.

2. Если ах2 + с = 0, с≠ 0 Уравнения данного вида решаются по алгоритму:

1) перенести слагаемые в правую часть;

2) найти все числа, квадраты которых равны числу с.

Например, х2 — 5 = 0,Это уравнение равносильно уравнению х2 = 5. Следовательно, надо найти все числа, квадраты которых равны числу 5. Таких чисел только два и — . Таким образом, уравнение х2 — 5 = 0 имеет два корня: x1 = , x2 = — и других корней не имеет.

3. Если ах2 + bх = 0, b ≠ 0. Уравнения такого вида решаются по алгоритму:

1) перенести общий множитель за скобки;

Например, х2 — 3х = 0. Перепишем уравнение х2 – 3х = 0 в виде х ( х – 3 ) = 0. Это уравнение имеет, очевидно, корни x1 = 0, x2 = 3. Других корней оно не имеет, ибо если в него подставить вместо х любое число, отличное от нуля и 3, то в левой части уравнения х ( х – 3 ) = 0 получится число, не равное нулю.

Итак, данные примеры показывают, как решаются неполные квадратные уравнения:

1) если уравнение имеет вид ах2 = 0, то оно имеет один корень х = 0;

2) если уравнение имеет вид ах2 + bх = 0, то используется метод разложения на множители: х (ах +b) = 0; значит, либо х = 0, либо ах + b = 0. В итоге получается два корня: x1 = 0; x2 = — ;

3) если уравнение имеет вид ах2 + с = 0, то его преобразуют к виду ах2 = — с и далее х2.= — В случае, когда — 0, т. е. — = m, где m>0, уравнение х2 = m имеет два корня

= , = —, (в этом случае допускается более короткая запись = .

Таким образом, неполное квадратное уравнение может иметь два корня, один корень, ни одного корня.

На втором этапе осуществляется переход к решению полного квадратного уравнения. Это уравнения вида ах2 + bx + c = 0, где a, b,c – заданные числа, а ≠ 0, х – неизвестное.

Любое полное квадратное уравнение можно преобразовать к виду , для того, чтобы определять число корней квадратного уравнения и находить эти корни. Рассмотриваются следующие случаи решения полных квадратных уравнений: D 0.

1. Если D 0, то квадратное уравнение ах2 + bx + c = 0 имеет два корня, которые находятся по формулам: ; (1)

Например, 3х2 +8х – 11 = 0. Решение: а = 3, b = 8, с = -11. D = b2 – 4ас = 82 – 4*3*(-11) = 64 + 132 = 196.

Так как D > 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формулам:

Составляется алгоритм решения уравнения вида ах2 + bx + c = 0.

1. Вычислить дискриминант D по формуле D = b2 – 4ас.

2. Если D 0, то квадратное уравнение ах2 + bx + c = 0 имеет два корня: ; .

Это алгоритм универсален, он применим как к неполным, так и к полным квадратным уравнениям. Однако неполные квадратные уравнения обычно по этому алгоритму не решают.

Математики – люди практичные, экономные, поэтому пользуются формулой: . (2)

Итак, можно сделать вывод, что квадратные уравнения можно решать подробно, используя сформулированное выше правило; можно – записать сразу формулу (2) и с ее помощью делать необходимые выводы. [1,98].

На третьем этапе рассматриваются приведенные квадратные уравнения, которые имеют вид х2 +px + q = 0 (3), где p и q – данные числа. Число p – коэффициент при х, а q – свободный член. Дискриминант уравнения равен: D = p2 – 4q. Рассматривают 3 случая:

1. D > 0, тогда уравнение (3) имеет два корня, вычисляемые по формуле . (4)

2. D = 0, тогда уравнение (3) имеет единственный корень, или, как горят, два совпадающих корня:

Видео:Математика в ВавилонеСкачать

Квадратные уравнения – сквозь века

Разделы: Математика

Цели урока:

Образовательные:
- расширение и углубление представлений учащихся о решении квадратных уравнений,
- обеспечение повторения, обобщения и систематизации знаний по решению квадратных уравнений.
Развивающие:
- способствовать формированию умений применять приемы обобщения, сравнения, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи,
- развитие творчества, умения анализировать,
Воспитательные:
- содействовать воспитанию интереса к математике, активности, умения общаться.

Задачи:

развивать интерес к предмету,
продолжать формирование общеучебных навыков,
сделать вывод о связи геометрии и алгебры,
дать историческое видение решения квадратных уравнений,
развивать различные способы анализа,
воспитывать математически грамотную личность.

1. Втупительное слово учителя

– Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Сегодня на уроке мы будем решать квадратные уравнения, которые уже решали на уроках алгебры в 8 классе. Только познакомимся с теми способами, которые не представлены в Вашем учебнике. Сегодня у нас урок-путешествие.

В развитии математики можно выделить четыре основных этапа:

Древний Вавилон
Античный мир
Эпоха Возрождения в Европе
Средневековый Восток

– Посмотрим, каким же образом решали квадратные уравнения в различные времена и похожи ли эти решения на современное.
Вспомним стандартный алгоритм решения квадратного уравнения.

2. Алгоритм решения квадратного уравнения:

Алгоритм строится на доске учителем, помогают учащиеся. По ходу построения схемы можно задавать наводящие вопросы:
– На что обращаем внимание, увидев квадратное уравнение?
– Стандартный вид, полное или неполное, приведенное или нет?
– Отмечаем другим цветом общий случай решения квадратного уравнения Повторяем теорему Виета.
– Теперь же отправимся в глубину веков и сначала посетим древний Вавилон.

3. Древний Вавилон (I тысячелетие до н.э.)

– Имена математиков этого времени не сохранились. Вся информация у современных ученых заимствована из клинописных табличек. Математика в то время считалась знанием для избранных, ей владели жрецы, которые тщательно оберегали информацию от непосвященных. Основным принципом того времени было указание к действию (делай как Я). Объяснение при решении уравнений в то время отсутствует. Вывода формул нет. Дается только рецепт решения конкретного квадратного уравнения, алгоритм носит общий характер. Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
При разборе задачи удобно разделить доску на две части. На одной записывать указания с клинописных табличек, на другой – стандартный алгоритм решения квадратного уравнения.

Задача 1.

Решение древних	Современное решение
Я вычел из площади одну сторону моего квадрата и получил 870.

Взял эту одну и разделил пополам

Умножил на саму себя.

Что является квадратом 29 ?

( = 29 )

Сложим то, что получили с первой половиной ()

Прибавили то, что было

x₁ = 30.х 2 – bx – c = 0

добавили свободный член

и получили формулу для четного коэффициента

Задаем вопрос: «Что настораживает, кажется странным?»

Отсутствует второй корень квадратного уравнения x₂ = – 29 (его легко найти по теореме, обратной теореме Виета). В древнем Вавилоне не оперировали с отрицательными числами, все задачи определялись практической жизнью. Поэтому получен только положительный корень.

Задача 2.

Длина и ширина вместе 14. Площадь 40. Найди длину и ширину.

Длина и ширина вместе 14. Площадь 40. О какой фигуре идет речь?

Можно догадаться, что речь идет о прямоугольнике со сторонами х и у.

Записываем систему уравнений, используя условие задачи.

– Каким образом можно решить систему?

1) Можно использовать способ подстановки.
2) Можно записать по теореме Виета квадратное уравнение и решить его.

Найди квадрат длины и ширины, взятых вместе:

Квадрат длины и ширины, взятых вместе равен 196. (Раскрываем скобки)

Возьми четыре площади – это 160.

Вычти из квадрата эти четыре площади, получишь 36.

196 – 160 = 36

(х – у)2 = 36

Найди корень. Это 6. x – y = 6

Предполагается, что длина больше ширины ( х > у). Это значит, что длина превосходит ширину на 6. Сложи длину и ширину с их разностью.

(x + y) + (x – y) =14 + 6. Это будет 20.
2x = 20. Две длины равны 20, значит одна длина 10.
x = 10.
Из суммы вычти разность.
(x + y) – (x – y) = 14 – 6
2y = 8
y = 8

Ответ: длина 8, ширина 6.

Для простых систем уравнений удобно было пользоваться стандартными способами, для более сложных – искали свои пути решения (это будет позднее).
Перенесемся теперь в Античный мир.

4. Античный мир (II век до н. э. – IV век н.э., Архимед, Евклид)

Метод решения квадратных уравнений разработал Евклид. Раньше уравнения решали по образцу, ничего не объясняя (существовало правило – делай как я).
В Античности появляется обязательное требования объяснять решение (почему что-то случилось, что произошло?). Геометрия в то время считалась наукой всех наук.
Поэтому теперь посмотрим на квадратное уравнение с точки зрения геометрии.

Задача 3.

Дано уравнение:

Отрицательных чисел в те века еще не знали, приблизился к ним только Диофант. Поэтому рассматриваем решение, используя только положительные числа.

В этом уравнении коэффициенты р > 0, q > 0. x = .

Записанное выражение напоминает теорему Пифагора. Если рассматривать , то проводя параллель с теоремой Пифагора можно догадаться, что находим катет (т.к. стоит знак минус). В этом случае гипотенуза равна , катет .

.

Выполним построение прямоугольного треугольника с помощью циркуля:

С центром в точке Р построим полуокружность радиусом РА = (РА – гипотенуза). От точки Р отложим вправо отрезок РМ = (отрезок РМ – катет).

В этом случае расстояния СМ и КМ:

СМ = x₁ = , КМ = x₂ = , (РС = РА = РК = ).

Для решения алгебраической задачи использовалась геометрия. В древности часто встречался синтез алгебры с геометрией.

Теперь отправимся на дальше.

5. Средневековый Восток (IX век н.э. аль-Хорезми)

В эти века все вычисления производились в уме, все объяснялось на словах, поэтому за решение очень сложно уследить, т.к. всё считается устно и вся информация держится в голове.
Задачи решались геометрическим способом. Мы знаем среднеазиатского математика аль-Хорезми, он дал классификацию линейных и квадратных уравнений и способы их решения. Общее решение квадратного уравнения он не рассматривал, т.к. его не интересовали уравнения, у которых не было ни одного положительного корня. Он старался записать уравнение так, чтобы все его члены выступали в качестве слагаемых, а не вычитаемых. Аль-Хорезми рассматривал пять типов квадратных уравнений:

ax 2 + bx = c ( квадраты и корни равны)
ax 2 + c = bx (квадраты и числа равны корням)
ax 2 = bx + c (корни и числа равны квадратам)
ax 2 = bx (квадраты равны корням)
ax 2 = c ( квадраты равны числу)

Почему? В то время еще не знали отрицательных чисел, Идея отрицательных чисел вносит общие методы решения, упрощает алгоритм. Кроме алгебраического способа нахождения корня уравнения аль-Хорезми обычно предлагал и геометрический.

Задача 4.

Квадрат и десять его корней равны 39. Рассмотрим геометрическое решение уравнения х 2 + 10х = 39.
Рисуем квадрат, сторона которого обозначается неизвестной величиной х.
x 2 – площадь квадрата со стороной x, 10x – площадь прямоугольника со сторонами 10 и x

Раздвои число корней (корней 10, раздвоили, получили 5). Построй большой квадрат.
Площадь маленького квадрата 25.Площадь заштрихованной фигуры 39.
Что можем найти? Площадь большого квадрата равна 39 + 25 = 64
Вся площадь целиком S_ABCD = 64. т.е. (х + 5) = 64, х = 3
Возникает вопрос: «Где ещё один корень?». Второй корень отрицательный. (По теореме Виета – 39 : 3 = – 13 ). х₂ = – 13
(Раздвоить прямоугольники удалось легко за счёт четного коэффициента. Этот наглядно, красиво, просто, но тяжело для других уравнений. Поэтому такой способ решения не развился дальше.)

6. Европа. Эпоха Возрождения (рассмотрим конкретное время – XVI век н. э. Франсуа Виет)

Невозможно сейчас представить математику специальных обозначений. Создателем алгебраической символики и формул по праву считается французский математик Франсуа Виет.. Он писал: «Искусство, которое я излагаю, ново или, по крайней мере, настолько испорчено временем и искажено влиянием варваров, что я счел нужным придать ему совершенно новый вид». Хотя символика Виета и обладала некоторыми недостатками, тем не менее это был огромный шаг вперед. А вот древние математики вполне обходились без буквенных обозначений и специальных правил оперирования с ними.
Сын прокурора, Виет получил юридическое образование и начал адвокатскую практику. Но вскоре он стал секретарем и домашним учителем в доме знатного дворянина-гугенота де Партеней. Тогда Виет очень увлекся изучением астрономии и тригонометрии. Знакомство Виета с Генрихом Наваррским, будущим королем Франции Генрихом IV помогло Виету занять видную придворную должность – тайного советника.
Одним из самых замечательных достижений Виета на королевской службе была разгадка шифра, в котором насчитывалось более 500 знаков, менявшихся время от времени. Этим шифром пользовались недруги французского короля в Нидерландах для переписки с испанским двором. Хотя французы часто перехватывали письма из Испании, расшифровать их никто не мог. Только Виет быстро нашел ключ. Испанцы не представляли себе всего могущества человеческого ума. Они думали, что французам помогает дьявол. Они даже жаловались римскому папе и просили его уничтожить дьявольскую силу.

Задача 5.

Рассмотрим уравнение х 2 – 6х – 16 = 0. Вводим новую переменную (на первый взгляд усложняем уравнение, но посмотрим, к чему это приведёт).

Мы хотим получить неполное квадратное уравнение, при каком значении а это получится?

Основа метода – любое полное уравнение заменой переменных сводим к неполному квадратному уравнению.
Эта идея дала толчок развитию математики. Появился вопрос: «А можно ли решать уравнения третьей, четвёртой, пятой и высших степеней. Существует ли общий метод решения более сложных уравнений?»
Формула решения квадратного уравнения известна с незапамятных времен. В XVI в. Итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции ( сложение, вычитание, умножение и деление. ) и извлечение корней степени не превышающей степень уравнения. Кроме того все уравнения данной степени можно «обслужить» одной формулой. После этого естественно возник вопрос: а есть ли похожие формулы для решения уравнений пятой степени и выше. Общей формулы для таких уравнений не существует. Это доказал молодой норвежский ученый Нильс Хенрик Абель. Однако, это не означает, что невозможно решить те или иные частные виды уравнений высоких степеней. Новые открытия в решении уравнений сделал французский ученый Эварист Галуа. Эварист Галуа погиб на дуэли в 20 лет. Свои результаты он изложил в письме, написанном в ночь перед поединком. Потребовались десятилетия, чтобы теория Галуа стала понятна математикам.

Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни. Алгебра и геометрия – взаимосвязаны.

Рассмотренные методы решения квадратных уравнений могут заинтересовать увлекающихся математикой учеников, дают возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.

В качестве домашнего задания можно предложить учащимся решить следующие квадратные уравнения различными способами.

1. x 2 – 10x – 9 = 0 решить способом в стиле Виета, аль-Хорезми.
2. x 2 – 10x + 9 = 0 решить способом в стиле Евклида.
3. 2x 2 – x – 1 = 0 решить способом в стиле Виета.
4. x 2 – 4x + 3 = 0 подобрать способ решения в стиле Евклида.
5. x 2 – 10x = 16 подобрать способ решения в стиле аль-Хорезми.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Методы решения уравнений в странах древнего мира

История алгебры уходит своими корнями в древние времена. Задачи, связанные с уравнениями, решались ещё в Древнем Египте и Вавилоне. Теория уравнений интересовала и интересует математиков всех времён и народов.

В Древнем Египте и Вавилоне использовался метод ложного положения (“фальфивое правило”)

Уравнение первой степени с одним неизвестным можно привести всегда к виду ах + Ь == с, в котором а, Ь, с — целые числа. По правилам арифметических действий ах = с — b,

Если Ь > с, то с — b число отрицательное. Отрицательные числа были египтянам и многим другим более поздним народам неизвестны (равноправно с положительными числами их стали употреблять в математике только в семнадцатом веке).

Для решения задач, которые мы теперь решаем уравнениями первой степени, был изобретен метод ложного положения.

В папирусе Ахмеса 15 задач решается этим методом. Решение первой из них позволяет понять, как рассуждал автор.

Египтяне имели особый знак для обозначения неизвестного числа, который до недавнего прошлого читали “хау” и переводили словом “куча” (“куча” или “неизвестное количество” единиц). Теперь читают немного менее неточно: “ага”.

bqt задача № 24 сборника Ахмеса:

“Куча. Ее седьмая часть (‘подразумевается: “дают в сумме”) 19. Найти кучу”.

Запись задачи нашими знаками:

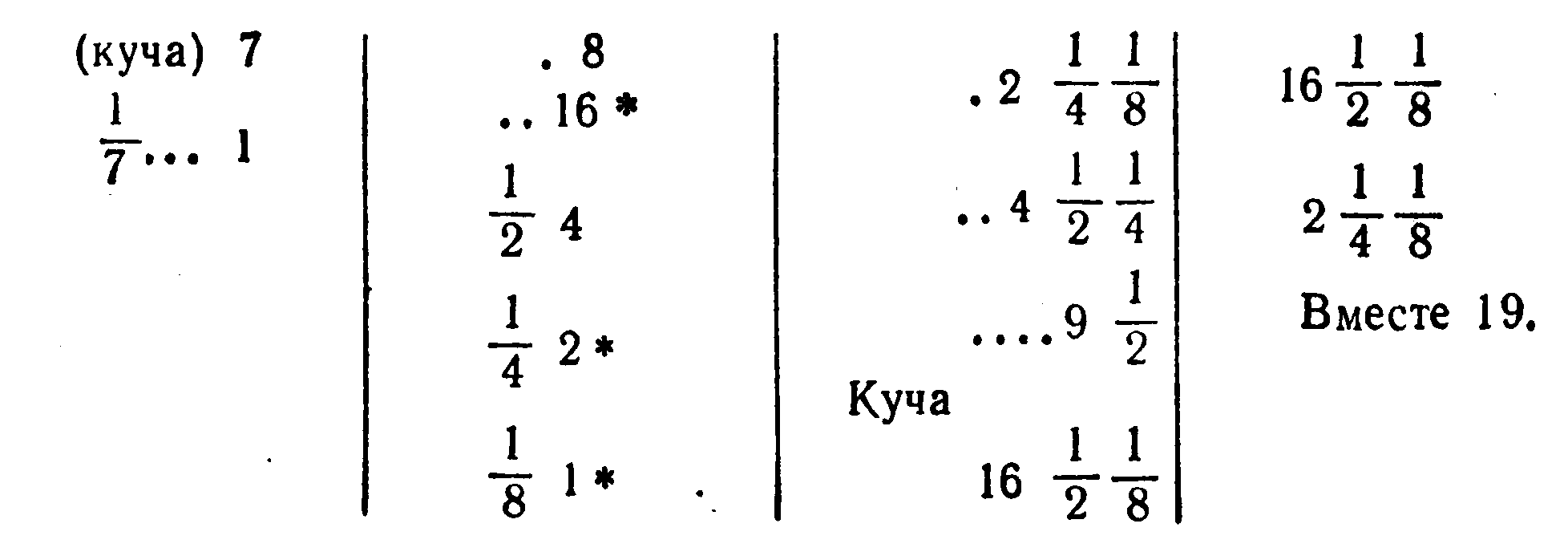
Решение Ахмеса может быть представлено в наших символах в следующих четырех столбцах:

Во многих задачах в начале или в конце встречаются слова: “Делай как делается”, другими словами: “Делай, как люди делают”.

Смысл решения Ахмеса легко понять.

Делается предположение, что. куча есть 7; тогда 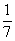ее часть есть 1. Это записано в первом столбце.

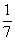
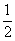
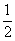
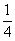
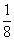
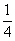
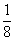
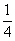
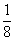
Во втором столбце записано, что при предположении х=7 куча и ее часть дали бы 8 вместо 19. Удвоение предположения дает 16. Автор, в уме очевидно, прикидывает, что дальше удваивать предположение нельзя, так как тогда получится больше 19. Он записывает 16, ставит перед числом две точки для обозначения удвоения первоначального предположения и отмечает значком (у нас — звездочкой) результат; для получения в сумме 19 первоначальное предположение надо умножить -на 2 с некоторым добавлением, так как для получения точного результата, 19, не хватает еще 19—16=3. Ахмес находит от 8, получает 4. Так как это больше нехватки 3, то на предположение умножить нельзя. Но от 8 есть 2, от восьми 1. Ахмес видит, что и первоначального результата дают точно те 3 единицы, которых не хватало. Отметив и значками, Ахмес убедился, что первоначальное предположение для кучи (7) надо помножить на

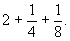
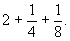
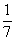
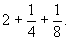
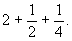
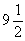
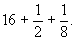
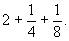
Умножение числа 7 на смешанное число Ахмес заменяет умножением смешанного числа на 7. В третьем столбце выписаны: часть искомой кучи есть , удвоенное это число: и учетверенное: . Сумма этих трех чисел, равная числу , есть произведение первоначального предположения 7 на .

Итак, куча равна .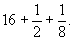

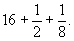
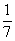
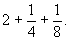
В последнем столбце Ахмес делает проверку, складывая полученное значение для кучи и его части . В сумме получается 19, и решение заканчивается обычным для автора заключением: “Будет хорошо”.

Способ решения, примененный Ахмесом, называется методом одного ложного положения. При помощи этого метода решаются уравнения вида ах == b. Его применяли как египтяне, так и вавилоняне.

У разных народов применялся метод двух ложных положений. Арабами этот метод был механизирован и получил ту форму, в которой он перешел в учебники европейских народов, в том числе в “Арифметику” Магницкого. Магницкий называет способ решения “фальшивым правилом” и пишет о части своей книги, излагающей этот метод:

Зело бо хитра есть сия часть,

Яко можеши ею все класть (вычислить. — И . Д.)

Не токмо что есть во гражданстве,

Но и высших наук в пространстве,

Яже числятся в сфере неба,

Якоже мудрым есть потреба.

Содержание стихов Магницкого можно вкратце передать так: эта часть арифметики весьма хитрая. При помощи ее можно вычислить не только то, что понадобится в житейской практике, но она решает и вопросы “высшие”, которые встают перед “мудрыми”.

Магницкий пользуется “фальшивым правилом” в форме, какую ему придали арабы, называя его “арифметикой двух ошибок” или “методой весов”.

Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Несмотря на высокий уровень развития алгебры в Вавилоне, • в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

. Как составлял и решал Диофант квадратные уравнения ,

В “Арифметике” Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

“Найти два числа, зная, что их сумма равна 20, а произведение — 96”.

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х, другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение

Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = —2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения

Ясно, что, выбирая в качестве неизвестного полу разность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).

Квадратные уравнения в Индии.

Задачи на уравнения встречаются уже в астрономическом трактате “Ариабхаттаим”, составленном в 449 г. индийским математиком и астрономом Арибхаттой. Но это уже раннее средневековье.

В Алгебраическом трактате ал-Хорезми даётся классификация линейных и квадратных уравнений.

Индий учёные знали решения неопределённых уравнений в целых числах (в том числе и в отрицательных, чего сам Диофант избегал).

Формула решений квадратного уравнения.

Греческий математик Герон (I или II век нашего летоисчисления) вывел формулу для решения квадратного равнения ax 2 + bx = c умножением всех членов на а и

прибавлением к обеим половинам уравнения :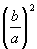

В индии пришли к более простому способу вывода, который встречается в школьных учебниках: они умножали на 4a и к обеим половинам по b 2 . Это даёт:

Индийские математики часто давали задачи в стихах.

Задача о лотосе.

Над озером тихим, с полмеры над водой,

Был виден лотоса цвет.

Он рос одиноко, и ветер волной

Нагнул его в сторону – и уж нет

Цветка над водой.

Нашёл его глаз рыбака

В двух мерах от места, где рос.

Сколько озера здесь вода глубока?

Тебе предложу я вопрос.

Ответ:

Из истории решения системы уравнений, содержащей одно уравнение второй степени и одно линейное

В древневавилонских текстах, написанных в III—II тысячелетиях до н. э., содержится немало задач, решаемых с помощью составления систем уравнений, в которые входят и уравнения второй степени. Вот одна из них.

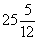
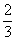
. “Площади двух своих квадратов я сложил: .Сторона второго квадрата равна стороны первого и еще 5”.

Соответствующая система уравнений в современной записи имеет вид:

Для решения системы (1) вавилонский автор возводит во втором уравнении у в квадрат и согласно формуле квадрата суммы, которая ему, видимо, была известна, получает:

Подставляя это значение у в первое из системы уравнений (1), автор приходит к квадратному уравнению:

Решая это уравнение по правилу, применяемому нами в настоящее время, автор находит х, после чего определяет у. Итак, хотя вавилоняне и не имели алгебраической символики, они решали задачи алгебраическим методом.

Диофант, который не имел обозначений для многих неизвестных, прилагал немало усилий для выбора неизвестного таким образом, чтобы свести решение системы к решению одного уравнения. Вот один пример из его “Арифметики”.

Задача 21. “Найти два числа, зная, что их сумма равна 20, а сумма их квадратов — 208”.

Эту задачу мы решили бы путем составления системы уравнений:

Диофант же, выбирая в качестве неизвестного половину разности искомых чисел, получает (в современных обозначениях):

Складывая эти уравнения, а затем вычитая одно из другого (все это Диофант производит устно), получаем

x = 2 + 10; у = 10 —2.

х 2 + у 2 = (г + lO) 2 + (10 — г) 2 == 2z 2 + 200.

z = 2; х = 2 + 10 = 12; у = 10 — 2 = 8.

Задача Диофанта №80 (Из II книги его “Арифметики”)

Найти 2 таких числа, чтобы сумма квадрата каждого из них с другим искомым числом дала полный квадрат,

Пусть первое число (I) будет s. Чтобы квадрат его •при прибавлении второго числа дал квадрат, второе число должно быть 2s + 1, так как в таком случае выполняется требование задачи: квадрат первого числа. сложенный со вторым, дает

s 2 + 2s + 1, то есть полный квадрат (s + 1) 2 .

Квадрат второго числа, сложенный с первым, должен также дать квадрат, то есть число (2s + I) 2 + s, равное

4s 2 + 5s + 1 == t 2

Положим, что t = 2s — 2; тогда t 2 = 4s 2 — 8s + 4. Это выражение должно равняться 4s 2 + 5s + 1. Итак, должно быть:

4s 2 — 8s + 4 == 4s 2 + 5s + l откуда s=

Значит, задаче удовлетворяют числа:

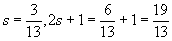
Почему Диофант делает предположение, что t==2s—2, он не объясняет. Во всех своих задачах (в дошедших до нас шести книгах его их 189) он делает то или другое предположение, не давая никакого обоснования.

Вообще содержание 6 книг таково:

В “Арифметике” 189 задач, каждая снабжена одним или несколькими решениями. Задачи ставятся в общем виде, затем берутся конкретные значения входящих в нее величин и даются решения.

Задачи книги I в большинстве определенные. В ней имеются и такие, которые решаются с помощью систем двух уравнений с двумя неизвестными, эквивалентных квадратному уравнению. Для его разрешимости Диофант выдвигает условие, чтобы дискриминант был полным квадратом. Так, задача 30— найти таких два числа, чтобы их разность и произведение были заданными числами,— приводится к системе

Диофант выдвигает “условие формирования”: требуется, чтобы учетверенное произведение чисел, сложенное с квадратом разности их, было квадратом, т. е. 4b + а 2 = с 2 .

В книге II решаются задачи, связанные с неопределенными уравнениями и системами таких уравнений с 2, 3, 4, 5, 6 неизвестными степени не выше второй.

Диофант применяет различные приемы. Пусть необходимо решить неопределенное уравнение второй степени с двумя неизвестными f 2 (х, у) ==0. Если у него есть рациональное решение (x 0 , y 0 ), то Диофант вводит подстановку

в которой k рационально. После этого основное уравнение преобразуется в квадратное относительно t, у которого свободный член f 2 ( x 0 , у 0 ) = 0. Из уравнения получается t 1 == 0 (это значение Диофант отбрасывает), t 2 — рациональное число. Тогда подстановка дает рациональные х и у.

В случае, когда задача приводилась к уравнению у 2 = ax 2 + bx + с, очевидно рациональное решение x 0 = О, y 0 =±C . Подстановка Диофанта выглядит так:

Другим методом при решении задач книги II Диофант пользовался, когда они приводили к уравнению у 2 == = a 2 x 2 + bx + с. Он делал подстановку

после чего х и у выражались рационально через параметр k:

Диофант, по существу, применял теорему, состоящую в том,; что если неопределенное уравнение имеет хотя бы одно рациональное решение, то таких решений будет бесчисленное множество, причем значения х и у могут быть представлены в виде рациональных функций некоторого параметра”

В книге II есть задачи, решаемые с помощью “двойного неравенства”, т. е. системы

Диофант рассматривает случай а = с, но впоследствии пишет, что метод можно применить и при а : с = т 2 , Когда а == с, Диофант почленным вычитанием одного равенства из другого получает и 2 — и 2 = b — d. Затем разность b — d раскладывается на множители b — d = п1 и приравнивает и + v = I, и — v = п, после чего находит

и = (I + п)/2, v = (I — n)/2, х — ( l 2 + п 2 >/4a — <b + d)/2a.

Если задача сводится к системе из двух или трех уравнений второй степени, то Диофант находит такие рациональные выражения неизвестных через одно неизвестное и параметры, при которых все уравнения, кроме одного, обращаются в тождества. Из оставшегося уравнения он выражает основное неизвестное через параметры, а затем находит и другие неизвестные.

Методы, разработанные в книге II, Диофант применяет к более трудным задачам книги III, связанным с системами трех, четырех и большего числа уравнений степени не выше второй. Он, кроме того, до формального решения задач проводит исследования и находит условия, которым должны удовлетворять параметры, чтобы решения существовали.

В книге IV встречаются определенные и неопределенные уравнения третьей и более высоких степеней. Здесь дело обстоит значительно сложнее, потому что, вообще говоря, неизвестные невозможно выразить как рациональные функции одного параметра. Но, как и раньше, если известны одна или две рациональные точки кубической кривой fз (х, у) == 0, то можно найти и другие точки. Диофант при решении задач книги IV применяет новые методы”

Книга V содержит наиболее сложные задачи; некоторые из них решаются с помощью уравнений третьей и четвертой степеней от трех и более неизвестных. Есть и такие, в которых требуется разложить данное целое число на сумму двух, трех или четырех квадратов, причем эти квадраты должны удовлетворить определенным неравенствам.,

При решении задач Диофант дважды рассматривает уравнение Пелля ax 2 + 1 = у 2 .

Задачи книги VI касаются прямоугольных треугольников с рациональными сторонами. К условию х 2 + у 2 == z 2 в них добавляются еще условия относительно площадей, периметров, сторон треугольников.

В книге VI доказывается, что если уравнение ax 2 + b == у 2 имеет хотя бы одно рациональное решение, то их будет бесчисленное множество. Для решения задач книги VI Диофант применяет все употребляемые им способы.

Кстати, в одном из древних рукописных сборников задач в стихах жизнь Диофанта описывается в виде следующей алгебраиче-юй загадки, представляющей надгробную надпись на его могиле

Прах Диофанта гробница покоит; дивись ей—и камень

Мудрым искусством его скажет усопшего век.

Волей богов шестую часть жизни он прожил ребенком.

И половину шестой встретил с пушком на щеках.

Только минула седьмая, с подругою он обручился.

С нею пять лет проведя, сына дождался мудрец;

Только полжизни отцовской возлюбленный сын его прожил.

Отнят он был у отца ранней могилой своей.

Дважды два года родитель оплакивал тяжкое горе,

Тут и увидел предел жизни печальной своей.

Задача-загадка сводится к составлению и решению уравнения:

откуда х = 84 = вот сколько лет жил Диофант.

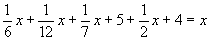
Неопределённое уравнение x 2 + y 2 = z 2

Такое неопределённое уравнение исследовали пиффагорийцы, целые решения которого поэтому называют “пифагоровыми тройками”, они нашли бесконечно много таких троек, имеющих вид:

Более систематическое исследование задач, эквивалентных кубическим уравнениям, относится только к эпохе эллинизма. Архимед в сочинении “О шаре и цилиндре” (книга II, предложение 4) свел задачу о рассечении шара плоскостью на два сегмента, объемы которых имели бы заданное отношение т : п (т > п), к нахождению высоты х большего сегмента из пропорции

(1)

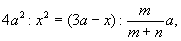
где а — радиус шара.

Архимед обобщает задачу: рассечь заданный отрезок а на две части х и а — х так, чтобы

(а — х) : с = S : х 2 , (2)

где с и S — заданные отрезок и площадь.

Заметив, что при такой общей постановке задача не всегда разрешима (имеются в виду только положительные действительные решения), Архимед приступает к ее исследованию с тем, чтобы наложить ограничения на с и S. Он говорит, что изложит полное решение задачи “в конце”, однако соответствующее место не сохранилось. Жившие на столетие позже Архимеда греческие геометры Диокл и Дионисодор уже не знали его. Они предложили собственные, гораздо более сложные решения, но никто из них не сумел провести анализ общего случая.

Только в VI в. н. э. комментатор Архимеда Евтокий нашел утраченное место. Архимед решает задачу с помощью двух конических сечений:

(3)

(4)

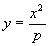
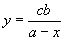
(здесь положено S = pb ). Оба уравнения легко получить из пропорции (2). Для выяснения необходимых условий Архимед переходит от пропорции (2) к кубическому уравнению

которое он выражает словесно как соотношение между объемами. Ясно, что уравнение (5) может иметь положительные корни, если

Итак, проблема сводится к нахождению экстремума х 2 (а — х).

Оставим пока в стороне вопрос о методе экстремумов Архимеда, мы вернемся к этому, когда будем говорить об инфинитезимальных методах древних. Скажем только, что Архимед полностью исследовал условия существования положительных вещественных корней уравнения (5), а именно:

1) если Sc 3 /27, то на участке (0, а) имеются два таких корня;

2) если Sc = 4a з /27, то имеется один корень (как сказали бы мы,— двукратный);

3) если Sc > 4a з /27, то корня нет.

Здесь 4а 3 /27 есть максимум х 2 (а — х) , достигаемый при х = 2а/3 . В конце письма, предпосланного книге “О коноидах и сфероидах” (греки называли сфероидами эллипсоиды вращения, прямоугольными коноидами — параболоиды вращения, а тупоугольными коноидами — полости двуполостных гиперболоидов вращения), Архимед пишет, что с помощью доказанных в книге теорем можно решить ряд задач, как, например: от данного сфероида или коноида отсечь сегмент плоскостью, проведенной параллельно заданной, так, чтобы отсеченный сегмент был равен данному конусу, цилиндру или шару. Перечисленные задачи, так же как и задачи о делении шара, сводятся к кубическим уравнениям, причем в случае тупоугольного коноида уравнение будет иметь вид

Из текста Архимеда можно заключить, что он проанализировал и решил это уравнение. Таким образом, Архимед рассмотрел кубические уравнения вида х 3 + ax + b = 0 при различных значениях a и b и дал метод их решения. Однако исследование кубических уравнений оставалось для греков трудной задачей, с которой, в ее общем виде никто, кроме Архимеда, не мог справиться. Решение отдельных задач, эквивалентных кубическим уравнениям, греческие математики получали с помощью нового геометрического аппарата конических сечений. Этот метод впоследствии восприняли математики стран ислама, которые сделали попытку провести полный анализ всех уравнений третьей степени.

Но еще до этого, и притом греческими математиками, был сделан новый решительный шаг в развитии алгебры: геометрическая оболочка была сброшена, и началось построение буквенной алгебры на основе арифметики. Это произошло в первые века нашей эры.

“История математики в древности” Э. Кольман.

“Решение уравнений в целых числах” Гельфонд.

“В мире уравнений” В.А.Никифоровский.

“История математики в школе” Г.И.Глейзер.

“Рассказы о старой и новой алгебре” И.Депман.

“Пифагор: рассказы о математике” Чистаков.

“Краткий очерк истории математики” Стройк Д.Я.

“Очерки по истории математики” Болгарский Б.В.

“История математики” (энциклопедия) под редакцией Юшкевича.

“Энциклопедический словарь юного математика” под редакцией Гнеденко.