Для формализации процесса решения уравнений и систем уравнений в алгебре множеств введем дополнительные определения.
Пусть J — универс и A(1),A(2). A(n) — заданные множества этого универса, X — неизвестное множество. Обозначим через F[A(1),A(2). A(n),X] и R[A(1),A(2). A(n),X] две формулы алгебры множеств. Множество X* называется частным решением уравнения
если F[A(1),A(2). A(n),X*] и R[A(1),A(2). A(n),X* ] определяют одно и то же множество.
Множество всех частных решений задает общее решениеуравнения (1).
Путем преобразования (используя законы алгебры множеств и следующие из них результаты) уравнение (1) может быть преобразовано к виду:
AX 
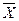


Пусть задана система уравнений в алгебре множеств. Путем эквивалентных преобразований система уравнений так же может быть преобразована к виду (2). Отсюда, для решения уравнения или системы уравнений в алгебре множеств, необходимо уметь находить общее решение уравнения типа (2).
Основные леммы, используемые при решении уравнений в алгебре множеств.
Для преобразования уравнений и систем уравнений в алгебре множеств к виду:
AX 
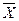


а так же для нахождения общего решения уравнения (1), используются следующие результаты, получающиеся из законов алгебры множеств.
Лемма 1.
A


Покажем, что из A


Доказательство от противного. Пусть A





Покажем, что из A 


Доказательство от противного. Пусть A 





Лемма 2.
А=В тогда и только тогда, если А 

Покажем, что из А=В следует А 

Если А=В, то А 







Покажем, что из А 

Если А 









Лемма 3.




Доказательство индукцией по n.
Лемма 4.


Доказательство следует из леммы 3 на основании принципа двойственности.
Полученные теоретические результаты позволяют находить общее решение уравнений и систем уравнений.
относительно неизвестного множества X.
Из леммы 1 следует, что уравнение (1) эквивалентно уравнению
F[A(1),A(2). A(n),X] 

После преобразований (применив, если это надо, закон де Моргана и другие законы алгебры множеств; на основании ассоциативного и дистрибутивного законов раскрыв скобки и приведя подобные члены) уравнение (2) становится эквивалентным уравнению
AX 
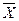


где А,В и С — некоторые множества, полученные в результате проведенных преобразований.
Из (3) по лемме 3 следует, что AX= 
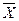


Из того, что AX= 
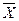

В 


Отсюда, уравнение (3) эквивалентно условиям :
В 



Так как X произвольное множество из универса, то из (3) следует, что условия :
В 


являются необходимыми и достаточными для того, чтобы исходное уравнение (1) имело решение.
Вместо условий (5) можно пользоваться эквивалентными им (на основании лемм1 и 3) условиями :
АВ 

Мы получили, что любое множество X* из универса, удовлетворяющее условиям (4), является частным решением уравнения (1).
Из условий (4) следует, что решение исходного уравнения (1) определяется следующим выражением:
X*= В 

где К — произвольное множество универса.
Таким образом, мы получили, что при любом К из универса выражение (7) представляет собой частное решение исходного уравнения (1), т.е. (7) определяет общее решение исходного уравнения (1). Из выражения (7) следует и оценка числа решений уравнения (1) N= 
A(В 










Здесь последнее равенство следует из условий (6).
Замечание.
Так как система уравнений алгебры множеств может быть приведена на основании выше доказанных лемм к виду (3), то результаты, полученные для случая решения уравнения, справедливы и для случая решения системы уравнений.
Видео:Множества и операции над нимиСкачать

Решение уравнений в алгебре множеств.
При решении уравнений в алгебре множеств исходят из того, что: 1) два множества равны тогда и только тогда, когда их симметрическая разность пуста; 2) определяются условия, при которых уравнения имеют решение [23].
Например, XUC=D. Преобразуем уравнение к виду (XUC)ÅD=Æ. Любое уравнение, в правой части которого указано пустое множество может быть преобразовано в уравнение с декомпозицией по X:
(F1IX)U(F2I 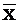
где F1, F2 – формулы, не содержащие X.
Очевидно, что объединение пусто тогда и только тогда, когда объединяемые множества пусты:
(F1IX)=Æ и (F2I 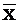
Два полученных уравнения и исходное уравнение имеют решение тогда и только тогда, когда:
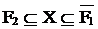
Поэтому необходимо определить F1, F2, что и является результатом решения уравнения.
Итак, (XUC)ÅD=Æ. Декомпозицию по X выполним, с помощью формулы симметрической разности двух множеств, использующей только операции объединения, пересечения и дополнения:
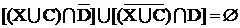
где 

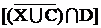

Выполним алгебраические операции:
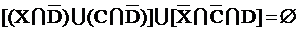
В этой формуле не хватает пересечения скобки 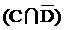

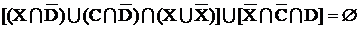
Далее раскрываем скобки и применяем законы алгебры множеств:
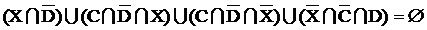
Здесь налицо поглощение 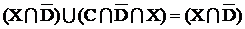

Выносим 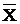

Обращаем внимание, что 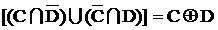

Таким образом: 
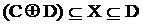
Само собой, в этом случае может быть множество решений для конкретных C, D.
Пусть C=, D=. Тогда (CÅD)=ÍD. X может быть, например, таким: X=, т.е. соотношение (CÅD)ÍXÍD – выполняется.
Пусть C=, при том же D=. Тогда (CÅD)= не включается в D=. В этом случае решения нет!
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Комбинаторные вычисления
При решении теоретико-множественных задач большое значение имеет определение мощности конечных множеств.
Очевидно, что |AUB|=|A|+|B|–|AIB|, т.е., когда А и В в «общем положении», т.е. пересекаются.
Кроме того, 
Нетрудно заметить, что |AÅB|=|A|+|B|–2|AIB|.
В дискретной математике имеется специальный раздел, занимающийся подсчетом и перечислением элементов в конечных множествах – комбинаторика или комбинаторный анализ. Вычисления на дискретных конечных математических структурах часто называют комбинаторными вычислениями.
Пусть в базе данных имеется n записей об объектах недвижимости (например, квартирах) в виде запроса (что требуется) и предложения (что имеется) Требуется найти такие пары записей, в которых предложение первой записи совпадает с запросом второй и, наоборот, предложение второй записи совпадает с запросом первой («подбор вариантов обмена»).
Допустим, на проверку варианта обмена тратится одна миллисекунда. Можно показать, что при сравнении каждой записи с каждой требуется n(n-1)/2 сравнений.
(6,7),(6,8),(7,8) – всего 28 вариантов: 8´7/2=28=7+6+5+4+3+2+1. Здесь отношение сравнения симметрично и сам с собой вариант не сравнивается.
Если n=100, то при указанном быстродействии, на сравнения уйдет 4,95 секунды. Но, если n=100000 (в задачах реальной размерности), то необходимо 1999950 секунд, т.е. без малого – 1389 часов! Столько ждать клиент вряд ли будет. Это и есть «проклятие размерности». И это только сравнение прямых вариантов, а существуют варианты, в которых число участников сделки больше двух.
Поэтому комбинаторные вычисления требуют предварительного анализа и ориентировочной количественной оценки исходных данных. Иначе, можно подумать, что компьютер просто «завис» и не выдаёт ответа. Здесь речь идет о сложности вычислений в смысле времени решения. В ряде задач комбинаторной сложности необходимо время, сравнимое с геологическими эпохами. Но есть еще и пространственная сложность – в смысле объема памяти. Ведь промежуточные результаты часто надо где-то хранить. В ряде задач требуется объем памяти, превышающий количество атомов во Вселенной.
Основным инструментом такого анализа сложности вычислений и является комбинаторика.
Основные понятия комбинаторики
Основная задача комбинаторики, как раздела дискретной математики, – пересчет и перечисление элементов в конечных множествах [24].
Если требуется определить, сколько элементов, принадлежащих заданному конечному множеству, обладает некоторым свойством или заданным набором свойств, то это задача пересчета. Если необходимо выделить все элементы множества, удовлетворяющие заданным свойствам, то это задача перечисления.
В некоторых задачах на исходном конечном множестве элементов определена целевая функция, причем нас интересуют элементы множества, соответствующие минимальному или максимальному значению этой функции. В этом случае решается задача оптимизации.
При этом под решением задачи оптимизации «в сильном смысле» понимается нахождение всех элементов минимизирующих (максимизирующих) целевую функцию, а под решением задачи оптимизации «в слабом смысле» – нахождение единственного произвольного элемента [24].
Рассмотрим основополагающие правила комбинаторики – правила суммы и произведения.
Пусть Х – конечное множество, состоящее из n элементов х. Тогда говорят, что элемент х из Х может быть выбран n способами и пишут |Х|=n. Эта запись совпадает с записью мощности множества Х.
Пусть Х1. Хk – попарно непересекающиеся множества, т.е. ХiIХj=Æ, i¹j.
Очевидно, что в этом случае

Таково комбинаторное правило суммы. Для k=2 оно формулируется следующим образом. Если объект х может быть выбран n способами из множества Х, а объект y из непересекающегося с ним множества Y, – другими m способами, то выбор «х или y» может быть осуществлен n+m способами.
Правило произведения для k=2 формулируется следующим образом. Если объект х может быть выбран n способами и после каждого из таких выборов объект y в свою очередь может быть выбран m способами, то выбор упорядоченной пары – вектора (х,y) может быть осуществлен n×m способами.
Тогда упорядоченные пары (x,y) описываются декартовым произведением
Выбор упорядоченной последовательности из k объектов вектора (х1,х2. хk) может быть осуществлен n1·n2·. ·nk способами, где ni – число способов выбора i-го объекта хi, i меняется от 1 до k (записывается: 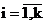
В частности, если все ni равны, что может быть, например, в случае, когда элементы принадлежат одному и тому же множеству, т.е. рассматривается декартово произведение Х k , то число способов равно n k .
Набор элементов хi1. xik из множества Х=<x1. xn> (вектор) называется выборкой (комбинацией) объема k из n элементов или, иначе, (n,k) выборкой.
Выборка называется упорядоченной, если порядок следования элементов в ней задан. Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными.
Если порядок следования элементов не является существенным, то такая выборка называется неупорядоченной.
В выборках могут допускаться и не допускаться повторения элементов, т.е. имеются выборки с повторением и выборки без повторений.
Размещения
Упорядоченная (n,k) выборка, в которой элементы могут повторяться, называется (n,k) размещением с повторениями.
Иными словами размещениями с повторениями из n элементов по k называют векторы длины k, составленные из n элементов множества Х.
Число размещений с повторениями из n элементов по k определяется оценкой соответствующего декартова произведения Х k n-элементного множества, обозначается 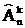
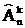
Таким образом, первый элемент вектора длины k выбирается n способами, второй – n способами и т.д.: n×n×. ×n=n k .
Пример. Сколькими способами можно оснастить две различные фирмы компьютерами трех типов?
Каждый способ оснащения есть выборка (3,2), вектор длины 2, составленный из 3-х элементного множества типов Т=<t1,t2,t3>. Поэтому число способов оснащения – число размещений с повторениями из 3 по 2:
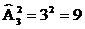
Получили различные упорядочения двухэлементных векторов из 3-х элементного множества, т.е. множество Т 2 .
Здесь каждый вектор соответствует способу оснащения. Видно, что, например, (t1,t2), (t2,t1) считаются разными способами, так как фирмы предполагаются различными («первая – первым типом», «вторая – вторым» и т.д.). Имеются повторения: (t1,t1), (t2,t2), (t3,t3).
В ряде задач необходимо определить число векторов длины k из n элементов данного множества без повторения элементов.
Если элементы упорядоченной (n,k) выборки попарно различны, то они называются (n,k) размещением без повторений или просто (n,k) размещением.
Число таких размещений без повторений обозначается 
Каждое (n,k) размещение без повторения является упорядоченной последовательностью длины k, элементы которой попарно различны и выбираются из множества с n элементами. Тогда первый элемент этой последовательности может быть выбран n способами, после каждого выбора первого элемента последовательности второй элемент может быть выбран n-1 способами и т.д., k-й элемент выбирается n-(k-1) способом:

Преобразуем эту формулу, умножая и деля ее на произведение чисел 1×2×××(n-k):
В частности, при k=0 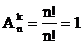

Пример. Сколькими способами из 3-х студентов можно назначить группу на прополку клубники в составе начальника и подчиненного?
Речь идет о выборе упорядоченных двухэлементных подмножеств множества студентов, состоящего из трех элементов (K=), т.е. о размещениях без повторений из 3 элементов по 2, поэтому:
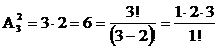
Подробнее, в виде векторов из номеров студентов, например, по журнальному списку, первая компонента которого обозначает номер студента-начальника, вторая – подчиненного:
Ясно, что здесь существенен порядок следования компонент и не может быть повторений (один студент не может быть начальником и подчиненным одновременно), поэтому это множество – подмножество декартового произведения.
Пример. Сколькими способами можно провести распределение 10 механизаторов по 3 сушильным установкам? Один механизатор назначается на одну сушильную установку.
Распределение механизаторов – размещение без повторений из 10 элементов по 3, поэтому:
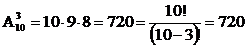
Перестановки
Рассмотрим различные упорядочения n элементного множества Х (вектора длины n, составленные из n элементного множества). В отличие от декартова произведения, полученные при этом векторы, отличаются лишь порядком следования элементов и называются перестановками без повторений из n элементов. Число перестановок без повторений из n элементов обозначается Pn. К перестановкам без повторений можно прийти, полагая, что осуществляется размещение без повторений из n элементов по n:
Считается, что 0!=1.
Пример. Сколько существует возможных последовательностей выполнения проверок финансовой деятельности трех подразделений?
Требуется получить число перестановок без повторений из трех элементов, т.е. Р3=3!=6.
Получим все эти последовательности:
Пример. Сколько можно составить пятизначных шифров-чисел, не кратных 5, из цифр 1,2,3,4,5 без повторений цифр?
Всего из пяти цифр можно составить Р5=5!=120 пятизначных шифров-чисел, но они будут включать и кратные 5. Сколько будет шифров кратных 5? Из данного набора чисел кратными 5 могут быть числа, содержащие 5 в младшем разряде. Если цифру 5 записать в младшем разряде, то остальные цифры 1,2,3,4 можно распределить по разрядам Р4=4!=24 способами. Таким образом, число пятизначных шифров из чисел 1,2,3,4,5 без повторения чисел и не кратных 5 будет 120-24=96.
Перестановки без повторений можно интерпретировать как различные варианты векторов, состоящих из неповторяющихся компонентов, получаемые перестановкой компонентов.
По аналогии при наличии одинаковых компонент в некотором векторе получаем задачу оценки так называемых перестановок с повторениями данного состава [23].
Рассмотрим вначале пример: сколько различных последовательностей – кодов можно получить, переставляя цифры в числе 010, т.е. векторов длины k=3 из 2-х элементного множества В=, содержащих два нуля.
Имеется всего три разряда, которые обозначим р1, р2, р3. Их можно переставить р3=3!=6 способами. Запишем различные получаемые сочетания разрядов и соответствующие коды:
Видно, что коды повторяются тогда, когда несущественен порядок следования разрядов с одинаковой цифрой 0 (р1,р3). Все это соответствует тому факту, что имеется два способа (2!) перестановки этих разрядов (р1,р3), (р3,р1) без изменения кода, т.е. неповторяющихся кодов будет меньше во столько раз, сколько имеется способов перестановки повторяющихся разрядов.
Рассмотрим более сложный случай.
Сколько различных «слов», не обязательно имеющих смысл, можно получить, переставляя буквы в слове «кишмиш»?
Здесь шесть букв слова можно переставить друг с другом р6=6!=720 способами, но в данном слове буквы «и» и «ш» повторяются дважды и при их перестановке слова могут повторяться. Сколько же существует вариантов перестановок этих букв без изменения слова? Первый вариант – исходный, второй – поменять местами буквы «и», третий – поменять местами буквы «ш», четвертый – поменять местами как буквы «и», так и буквы «ш». Всего четыре варианта. С учетом того, что эти четыре варианта участвуют в порождении 720 способов, получим 720/4=180 различных «слов». Можно показать, что число раз, во сколько уменьшается количество слов по сравнению с числом перестановок без повторений, представляет собой произведение факториалов количества повторяющихся букв.
Таким образом, если из n элементов множества Х=<x1,x2. xn> составлен вектор V длины k, причем каждому i-му компоненту можно поставить в соответствие число ki, указывающее его число повторений в V, то задан вектор S=(k1,k2. kn), который называется составом данного вектора.
Так, для Х= и V=(010223), состав: S=(2,1,2,1).
Векторы одного и того же состава, отличающиеся лишь порядком компонент, называются перестановками с повторениями данного состава.
Общая формула числа перестановок с повторениями данного состава имеет вид
Р(k1,k2. kn)= 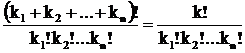
Пример. Сколько различных кодовых последовательностей можно получить перестановками кода 102202030?
Такому вектору, составленному из элементов множеств соответствует вектор состава (1,4,3,1), поэтому число различных кодовых комбинаций определяется как число перестановок с повторениями этого состава
Р(1,4,3,1)= 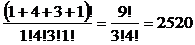
Сочетания
В ряде комбинаторных задач требуется определить число k-элементных подмножеств множества из n элементов. В этом случае порядок следования компонентов несущественен, т.е. производится неупорядоченная выборка.
В результате получают так называемые сочетания без повторения.
Сочетаниями без повторений из n элементов по k называются отличающиеся друг от друга хотя бы одним элементом выборки длины k, составленные из n элементного множества.
Число сочетаний без повторений из n элементов по k, обозначаемое как 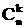

Пример. Определить число двухэлементных подмножеств множества, состоящего из трех элементов. Перечисляем все двухэлементные подмножества множества Х=<х1,х2,х3>:
Здесь мы имеем дело с сочетаниями из 3-х по 2:
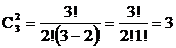
Это величина в 2! раза меньше, чем число размещений из 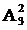
Пример. Сколькими способами можно выбрать 3 различных комбайна из 5 имеющихся?
Число размещений из 5 по 3 без повторений: 
Один и тот же набор комбайнов можно получить различными способами, например, векторы (а,b,с) и (b,а,с) дают один и тот же набор. Поскольку три элемента можно переставить Р3=3!=6 способами, то число способов выбора различных 3 комбайнов равно

В ряде комбинаторных задач требуется подсчитывать число различных составов векторов длины k из n элементного множества. Такие векторы-составы называются сочетаниями с повторениями из n элементов по k.
Например, требуется составить механизированные бригады из 3 комплексов 2 типов и определить количество таких бригад. Порядок следования комплексов в векторе бригады роли не играет, а каждая бригада задается вектором длины 3 из 2 элементов, порядок компонент которого роли не играет.
Получаем сочетания с повторениями из 2 элементов по 3:
где m означает тип комплекса.
Итак, возможно построить бригаду из трех комплексов первого типа, трех комплексов второго типа, двух комплексов второго типа и одного первого и, наконец, двух комплексов первого типа и одного второго, т.е. четырьмя способами.
Определение числа сочетаний с повторениями можно произвести следующим образом [24].
Каждому сочетанию с повторениями из 2 по 3 ставится в однозначное соответствие вектор длины n+k-1=2+3-1=4, состоящий из 3 нулей и n-1=1 единицы:
| Количество комплексов 1-го типа | Разделитель | Количество комплексов 2-го типа | Состав вектора бригады |
| 000 | 1 | (m1,m1,m1) | |
| 0 | 1 | 00 | (m1,m2,m2) |
| 00 | 1 | 0 | (m1,m1,m2) |
| 1 | 000 | (m2,m2,m2) |
В таком случае число сочетаний с повторениями, которое обозначается 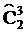

В общем случае, это выражение имеет вид
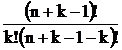
что соответствует выражению

Например, требуется составить подразделения из 6 рабочих 4 специальностей и определить количество способов формирования таких подразделений.
Получаем сочетания с повторениями из 4-х элементов по 6:

Треугольник Паскаля.
Сочетаниями без повторений занимался еще великий Паскаль. Он предложил специальную таблицу значений сочетаний без повторений.
Значения 
| k n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0 | 1 | ||||||||
| 1 | 1 | 1 | |||||||
| 2 | 1 | 2 | 1 | ||||||
| 3 | 1 | 3 | 3 | 1 | |||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
Заметим, что 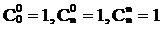
Этот треугольник удивительно красив своей математической красотой, и в его числах можно при желании отыскать различные закономерности. Его можно представить несколько иначе – в виде [26]: равнобедренного треугольника (рис. 10).
Рис. 10. Треугольник Паскаля
Здесь каждое число, кроме единиц на боковых сторонах, является суммой двух чисел, стоящих над ним. Поэтому:
(приводим к общему знаменателю)
(выносим n! за скобку в знаменателе)
Из этого соотношения и вытекает эффективный способ рекуррентного вычисления значений биномиальных коэффициентов.
Докажем соотношение 1)
Это может использоваться при вычислениях, например, вместо 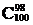
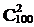
Докажем соотношение 2)
Бином Ньютона
Имеется формула, называемая биномом Ньютона, которая использует выражения числа сочетаний с повторениями
где а, b – действительные или комплексные числа.
Коэффициенты 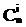
Докажем формулу бинома Ньютона по индукции. Доказательство по индукции предполагает:
1) базис индукции – доказательство того, что формула верна для конкретного n, например, для n=1. В нашем случае мы убедились, что формула верна для n=2,3,4. Убедимся, что она верна и для n=1.
2) индукционный шаг. Предполагая, что формула верна для некоторого n, убеждаются, что тогда она верна и для n+1.
3) при истинности шагов 1 и 2 заключают, что формула верна для любого n.
Приступим к индукционному шагу.
Возьмем выражение 
Преобразуем полученное выражение:
Для выполнения индукционного шага необходимо показать, что это выражение равно выражению:
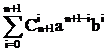
Рассмотрим подвыражение выражения (1): 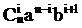
Получим 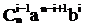
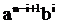


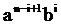
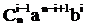
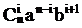
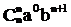
Нетрудно видеть, что 

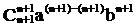
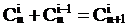
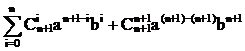

По индукции получаем, что формула бинома Ньютона верна для любого n.
С использованием бинома Ньютона докажем следствие №1 о количестве подмножеств множества из n элементов:
Рассмотрим следствие №2: 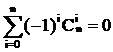
На использовании бинома Ньютона основано понятие производящей функции – функции, позволяющей получать комбинаторные числа без вычисления факториала:

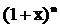
При n=1 получаем 1+x, т.е. 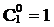

При n=2 получаем (1+x) 2 =1+2x+x 2 , т.е. 
Видео:3.10 Пример - доказательство равенства двух множествСкачать
Решение некоторых задач по теории множеств
Разделы: Математика
На математическом кружке вместе с учащимися рассматривался ряд задач, благодаря наглядности которых, процесс решения становится понятным и интересным. На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.
Введем определение множества, а так же некоторые обозначения.
Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.
Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.
Можно сделать такую запись определения множества:

“
” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.
Два множества будем называть равными, если они состоят из одних и тех же элементов
Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если 

Графически это выглядит так (рис.1):
Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.
Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).
Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или ” ключевое в понимании элементов входящих в объединение множеств.
Это определение можно записать с помощью обозначений:
А υ В, где
где “ υ ” – знак объединения,
“ / ” – заменяет слова ”таких что“
Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:
А ∩ В = С, где
“∩“ – знак пересечения. (рис.3)
Обозначим буквой Е основное или универсальное множество, где 



Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается Ā Е или Ā (рис.4)

Примерами для понимания этих понятий являются свойства:
А 
Свойства дополнения имеют свойства двойственности:
А
А
Введем еще одно понятие – это мощность множества.
Для конечного множества А через m (A) обозначим число элементов в множестве А.
Из определение следуют свойства:
Для любых конечных множеств справедливы так же утверждения:
m (A
m (A∩B) = m (A) + m (В) – m (А
m (A

А теперь рассмотрим ряд задач, которые удобно решать, используя графическую иллюстрацию.
Задача №1
В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек.
По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 9 человек. Ни одной задачи не решили 3 человека.
- Сколько учащихся решили все задачи?
- Сколько учащихся решили только две задачи?
- Сколько учащихся решили только одну задачу?
Задача № 2
Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.
Сколько студентов успешно решили только одну контрольную работу?
Задача № 3
В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников.
Сколько учеников пользуются только одним видом транспорта?
Решение задачи № 1
Запишем коротко условие и покажем решение:
- m (Е) = 40
- m (А) = 20
- m (В) = 18
- m (С) = 18
- m (А∩В) = 7
- m (А∩С) = 8
- m (В∩С) = 9
m (А



Обозначим разбиение универсального множества Е множествами А, В, С (рис.5).
К 1 – множество учеников, решивших только одну задачу по алгебре;
К 2 – множество учеников, решивших только две задачи по алгебре и геометрии;
К 3 – множество учеников, решивших только задачу по геометрии;
К 4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;
К 5 – множество всех учеников, решивших все три задачи;
К 6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;
К 7 – множество всех учеников, решивших только задачу по тригонометрии;
К 8 – множество всех учеников, не решивших ни одной задачи.
Используя свойство мощности множеств и рисунок можно выполнить вычисления:
- m (К 5 ) = m (А∩В∩С)= m (А
В
С) — m (А) — m (В) — m (С) + m (А∩В) + m (А∩С) + m (В∩С)
- m (К 5 ) = 37-20-18-18+7+8+9=5
- m (К 2 ) = m (А∩В) — m (К 5 ) = 7-5=2
- m (К 4 ) = m (А∩С) — m (К 5 ) = 8-5=3
- m (К 6 ) = m (В∩С) — m (К 5 ) = 9-5=4
- m (К 1 ) = m (А) — m (К 2 ) — m (К 4 ) — m (К 5 ) = 20-2-3-5=10
- m (К 3 ) = m (В) — m (К 2 ) — m (К 6 ) — m (К 5 ) = 18-2-4-5=7
- m (К 7 ) = m (С) — m (К4) — m (К 6 ) — m (К 5 ) = 18-3-4-5 =6
- m (К 2 ) + m (К 4 ) + m (К6) = 2+3+4=9 – число учеников решивших только две задачи;
- m (К 1 ) + m (К 3 ) + m (К 7 ) = 10+7+6=23 – число учеников решивших только одну задачу.
Ответ:
5 учеников решили три задачи;
9 учеников решили только по две задачи;
23 ученика решили только по одной задаче.
С помощью этого метода можно записать решения второй и третьей задачи так:
Решение задачи № 2
- m (А
В) = 33
- m (А
С) = 31
- m (В
С) = 32
- m (К 2 ) + m (К 4 ) + m (К 6 ) + m (К 5 ) = 20
Найти m (К 1 ) + m (К 3 ) + m (К 7 )
- m (АUВ) = m (К 1 ) + m (К 2 ) + m (К 3 ) + m (К 4 ) + m (К 5 ) + m (К 6 ) = m (К 1 ) + m (К 3 ) + 20 = 33 =>
- m (К 1 ) + m (К 3 ) = 33 – 20 = 13
- m (АUС) = m (К 1 ) + m (К 4 ) + m (К 2 ) + m (К 5 ) + m (К 6 ) + m (К 7 ) = m (К 1 ) + m (К 7 ) + 20 = 31 =>
- m (К 1 ) + m (К 7 ) = 31 – 20 = 11
- m (ВUС) = m (К 3 ) + m (К 2 ) + m (К 5 ) + m (К 6 ) + m (К 7 ) + m (К 4 ) = m (К 3 ) + m (К 7 ) + 20 = 32 =>
- m (К 3 ) + m (К 7 ) = 32 – 20 = 12
- 2m (К 1 ) + m (К 3 ) + m (К 7 ) = 13+11=24
- 2m (К 1 ) + 12 = 24
- m (К 3 )= 13-6=7
- m (К 7 )=12-7=5
- m (К 1 ) + m (К 3 ) + m (К 7 ) = 6+7+5=18
Ответ:
Только одну контрольную работу решили 18 учеников.
Решение задачи № 3
- m (Е) = 35
- m (А∩В∩С)= m (К 5 ) = 6
- m (А∩В)= 15
- m (А∩С)= 13
- m (В∩С)= 9
Найти m (К1) + m (К3) + m (К 7 )
- m (К 2 ) = m (А∩В) — m (К 5 ) = 15-6=9
- m (К 4 ) = m (А∩С) — m (К 5 ) = 13-6=7
- m (К 6 ) = m (В∩С) — m (К 5 ) = 9-6=3
- m (К 1 ) + m (К 3 ) + m (К 7 ) = m (Е) — m (К 4 ) — m (К 2 ) — m (К 6 ) — m (К 5 ) = 35-7-9-3-6=10
Ответ:
Только одним видом транспорта пользуется 10 учеников.
Литература: А.Х. Шахмейстер «Множества. Функции. Последовательности»
📹 Видео
Операции над множествамиСкачать

9 класс, 2 урок, Множества и операции над нимиСкачать

Множества. Операции над множествами. 10 класс алгебраСкачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебраСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Математика | Решение уравненийСкачать

Как использовать интеграл в обычной жизни. Математик МГУ и Савватеев #shortsСкачать

Линейное уравнение с одной переменной. 6 класс.Скачать

Круги Эйлера. Логическая задача на множества. Иностранные языкиСкачать

Математика это не ИсламСкачать

Пересечение и объединение множеств.Решение примеровСкачать

Уравнение с модулемСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

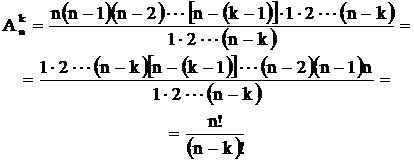
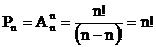


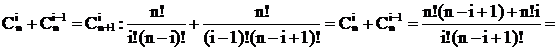
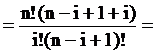

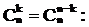
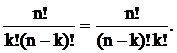

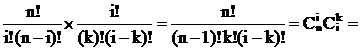

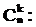

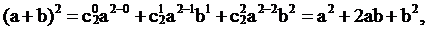
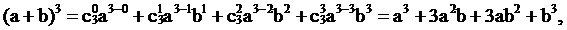

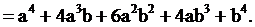
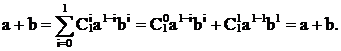
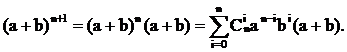

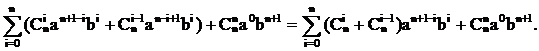
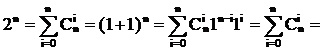

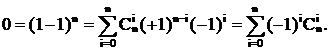
 ” – принадлежит;
” – принадлежит; 






