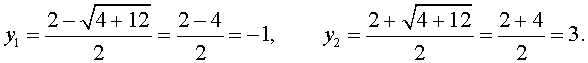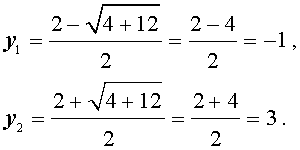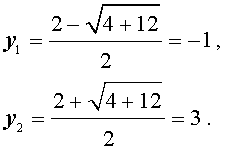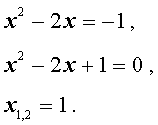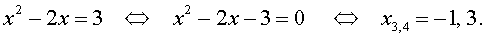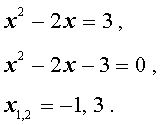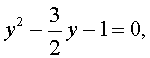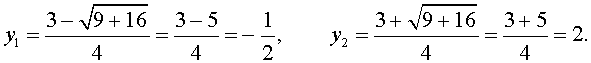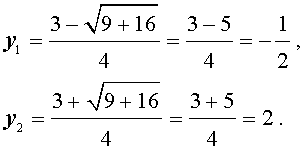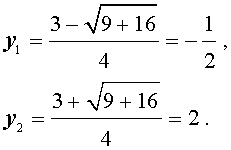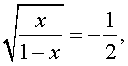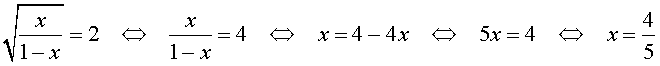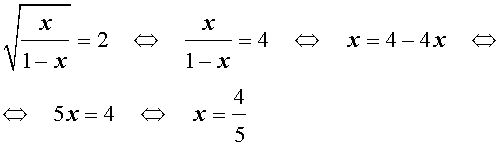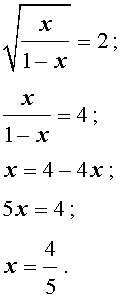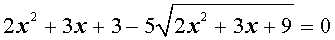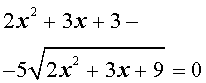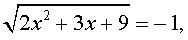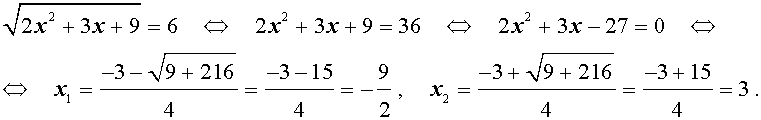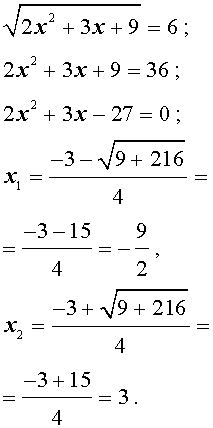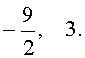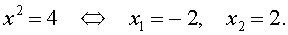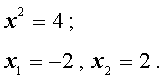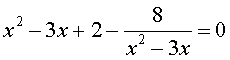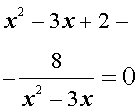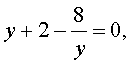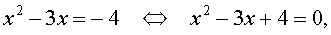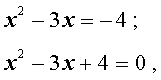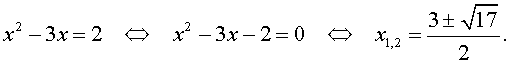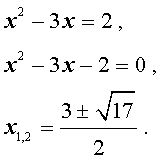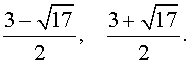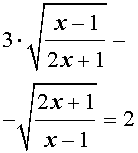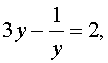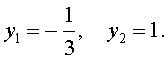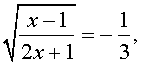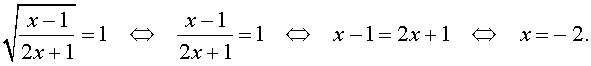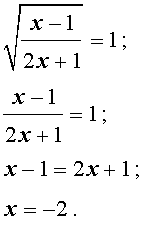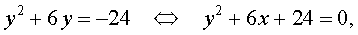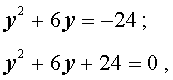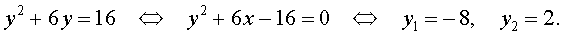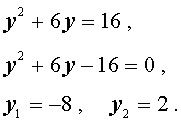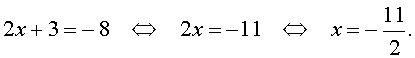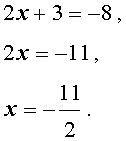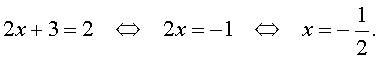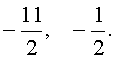трехчленные уравнения и уравнения вида
(ax + b)(ax + b + c)(ax +
+ b + 2c)(ax + b + 3c) = d , левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
 | Трёхчленные уравнения |
 | Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии |
 | Возвратные (симметричные) уравнения 3-ей степени |
 | Возвратные (симметричные) уравнения 4-ой степени |
 | Обобщенные возвратные уравнения 4-ой степени |
Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .
- Трехчленные уравнения
- Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
- Алгебра
- Квадратные уравнения
- Определение квадратного уравнения
- Решение квадратного уравнения
- Уравнения, сводящиеся к квадратным
- Задачи, решаемые с помощью квадратных уравнений
- Теорема Виета
- Разложение квадратного трехчлена на множители
- Дробно-рациональные уравнения
- Решение уравнений, сводящихся к квадратным
- Биквадратные уравнения
- Метод разложения на множители
- Метод замены переменной
- Выделение полного квадрата
- Примеры
- 💡 Видео
Видео:Решение уравнений сводящихся к квадратным уравнениям. Биквадратные уравнения – 8 класс алгебраСкачать

Трехчленные уравнения
Трёхчленными уравнениями называют уравнения вида
| a f 2 (x)+ b f (x) + c = 0, | (1) |
а также уравнения вида
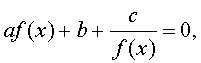 | (2) |
где a, b, c – заданные числа, а f (x) – некоторая функция.
Для того, чтобы решить трехчленное уравнения вида (1), обозначим
| y = f (x), | (3) |
тогда уравнение (1) станет квадратным уравнением относительно переменной y :
| ay 2 + by + c = 0 . | (4) |
Затем найдем корни уравнения (4), а после этого, подставив каждый из найденных корней в равенство (3), решим полученное уравнение относительно x .
Для того, чтобы решить трехчленное уравнение вида (2), сначала введем обозначение (3), а затем умножим полученное уравнение на знаменатель. В результате уравнение (2) примет вид (4), а схема решения уравнения (4) уже описана выше.
Покажем, как это осуществляется на примерах.
Пример 1 . Решить уравнение
| (x 2 – 2x) 2 – – 2(x 2 – 2x) – 3 = 0 . | (5) |
Решение . Если обозначить
| y = x 2 – 2x , | (6) |
то уравнение (5) превратится в квадратное уравнение
| y 2 – 2y – 3 = 0 . | (7) |
В первом случае из равенства (6) получаем:
Во втором случае из равенства (6) получаем:
Пример 2 . Решить уравнение
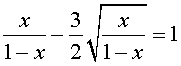 | (8) |
Решение . Если обозначить
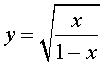 , , | (9) |
то уравнение (8) превратится в квадратное уравнение
которое эквивалентно уравнению
| 2y 2 – 3 y – 2 = 0 . | (10) |
В первом случае из равенства (9) получаем уравнение:
Во втором случае из равенства (9) получаем:
Ответ :
Пример 3 . Решить уравнение
Решение . Если обозначить
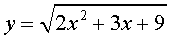 | (12) |
то уравнение (11) превратится в квадратное уравнение
которое эквивалентно уравнению
| y 2 – 5y – 6 = 0 . | (13) |
В первом случае из равенства (12) получаем уравнение:
Во втором случае из равенства (12) получаем:
Ответ :
Пример 4 . Решить биквадратное уравнение
| x 4 – x 2 – 12 = 0 . | (14) |
Решение . Если обозначить
| y = x 2 , | (15) |
то уравнение (14) превратится в квадратное уравнение
| y 2 – y – 12 = 0 . | (16) |
В первом случае из равенства (15) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (15) получаем:
Пример 5 . Решить уравнение
Решение . Если обозначить
| y = x 2 – 3x, | (18) |
уравнение (17) превращается в уравнение
которое при умножении на y принимает вид
| y 2 + 2y – 8 = 0 . | (19) |
В первом случае из равенства (18) получаем квадратное уравнение:
которое решений не имеет.
Во втором случае из равенства (18) получаем:
Ответ :
Пример 6 . Решить уравнение
Решение . Если обозначить
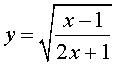 , , | (21) |
уравнение (20) превращается в уравнение
которое при умножении на y принимает вид
| 3y 2 – 2y – 1 = 0 . | (22) |
В первом случае из равенства (21) получаем уравнение
Во втором случае из равенства (21) получаем:
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
| (ax + b)(ax + b + + c)(ax + + b + 2c)(ax + + b + 3c) = d , | (23) |
где a, b, c, d – заданные числа, и заметим, что левая часть этого уравнения представляет собой произведение четырёх последовательных членов арифметической прогрессии, первый член которой равен ax+b , а разность равна c .
Схема решения уравнений вида (23) заключается в следующем.
| y = ax + b. | (24) |
Тогда уравнение (23) примет вид:
| y (y + c)(y + + 2c)(y + 3c) = d . | (25) |
Перегруппируем сомножители в левой части уравнения (25) следующим образом:
| [y (y + 3c)][(y + + c)(y + 2c)] = d . | (26) |
Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (26), то получим:
| [y 2 + 3cy][y 2 + + 3cy + 2c 2 ] = d . | (27) |
Если теперь в уравнении (27) обозначить
| z = y 2 + 3cy , | (28) |
то уравнение (27) станеи квадратным уравнением
| z 2 + 2c 2 z – d = 0 . | (29) |
Для того, чтобы найти корни уравнения (23), остаётся решить уравнение (29), затем для каждого корня уравнения (29) решить уравнение (28) относительно y , а затем в каждом из полученных случаев решить уравнение (24) относительно x .
Пример 7 . Решить уравнение
| (2x + 3)(2x + 5)(2x + + 7)(2x + 9) = 384 . | (30) |
Решение .Если обозначить
| y = 2x + 3, | (31) |
уравнение (30) превращается в уравнение
| y (y + 2)(y + + 4)(y + 6) = 384 . | (32) |
Перегруппируем сомножители в левой части уравнения (32):
| [y (y + 6)][(y + + 2)(y + 4)] = 384 . | (33) |
Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (33), то уравнение (33) примет вид:
| [y 2 + 6y][y 2 + + 6y + 8] = 384 . | (34) |
Если теперь обозначить
| z = y 2 + 6y , | (35) |
то уравнение (34) станет квадратным уравнением
| z 2 + 8 z – 384 = 0 . | (36) |
В первом случае из равенства (35) получаем уравнение:
которое корней не имеет.
Во втором случае из равенства (35) получаем:
В первом из этих случаев, из равенства (31) получаем:
Во втором случае из равенства (31) получаем:
Ответ :
Видео:Уравнения, сводящиеся к квадратным | Квадратный трёхчлен #4 | Ботай со мной #023 | Борис ТрушинСкачать

Алгебра
Видео:Урок 99 Решение целых рациональных уравнений, сводящихся к квадратным уравнениям (8 урок)Скачать

Квадратные уравнения
План урока:
Видео:Решение уравнений, сводящихся к квадратным уравнениям (урок 2)Скачать

Определение квадратного уравнения
Изучая понятие многочленов, мы познакомились с квадратными трехчленами. Так называют полином 2-ой степени, содержащий только одну переменную. Если его приравнять к нулю, то получится квадратное уравнение. Дадим определение квадратному уравнению:
Приведем несколько конкретных примеров:
- 5х 2 + 4х + 7 = 0
- – 3х 2 + х – 1,5 = 0
- 0,05х 2 + 99,568х – 47,21 = 0
Числа a, b и с называют коэффициентами квадратного уравнения. Отметим, что числа b и c могут равняться нулю, и в этом случае соответствующее слагаемое просто не записывается:
Эти уравнения именуют неполными.
Если же коэффициент а=0, то получается линейное уравнение, которое мы уже умеем решать:
Естественно, что для обозначения переменной может использоваться любая буква, а не только х:
- у 2 + 3,5х – 93 = 0
- – 32z 2 + 11z – 78 = 0
Для обозначения коэффициентов могут использоваться специальные термины:
- а – старший коэффициент;
- b– второй коэффициент;
- с – свободный член.
Неполные квадратные уравнения можно очень легко решить. Сначала рассмотрим пример, в котором b = 0:
Перенесем вправо свободный коэффициент:
Далее поделим на старший коэффициент обе части равенства:
Понятно, что х равен квадратному корню из 9. Напомним, что у каждого положительного числа есть два квадратных корня! Один из них является положительным числом и называется арифметическим, а другой противоположен ему по знаку. Поэтому можно записать, что
Иногда используют более короткую запись:
Не любое квадратное уравнение, у которого нет второго коэффициента b, будет иметь решение. Рассмотрим уравнение
Будем решать его таким же путем, перенося свободный коэффициент c вправо и деля уравнение на старший коэффициент a:
Квадрат действительного числа не может быть отрицательным. Значит, данное уравнение не будет иметь корней.
Сформулируем общий алгоритм решения неполных квадратных уравнений такого типа:
Теперь изучим неполные уравнения, в которых нет свободного слагаемого с. Рассмотрим их на примере:
Слева вынесем переменную х за скобки:
Теперь слева находится произведение двух множителей, а справа – ноль. Очевидно, что произведение может равняться нулю лишь в том случае, когда один из составляющих его множителей (х или 7х + 21) является нулем.
Зная это, запишем:
х = 0 или 7х + 21 = 0
Получили корень х = 0 и ещё одно линейное уравнение, которое легко решить:
В результате имеем два корня: 0 и – 3
Опишем общий алгоритм решения этих неполных уравнений:
Видео:Биквадратные уравнения. 8 класс алгебра.Скачать

Решение квадратного уравнения
Найти решение квадратного уравнения, если оно полное, достаточно тяжело. Нам поможет формула квадрата суммы:
(а + b) 2 = a 2 + 2ab + b 2
Напомним, что с ее помощью можно разложить на множители некоторые квадратные полиномы:
х 2 + 8х + 16 = х 2 + 2•4•х + 4 2 = (х + 4) 2
Конечно, здесь нам повезло с квадратным трехчленом – его коэффициенты позволяли воспользоваться формулой квадрата суммы. Однако похожие преобразования можно выполнить и тогда, когда коэффициенты не такие удобные:
х 2 + 8х + 20 = х 2 + 8х + 16 + 4 =(х 2 + 8х + 16) + 4 = (х 2 + 2•4•х + 4 2 ) + 4 =
Здесь мы разложили число 20 на сумму 16 + 4, чтобы можно было часть выражения «свернуть» формулой квадрата суммы. Такой прием можно применить вообще к любому квадратному трехчлену:
4х 2 + 10х + 4 = (2х) 2 + 2•2х•2,5 + 2,5 2 – 2,5 2 + 4 = (2х + 2,5) 2 – 2,5 2 + 4 =
= (2х + 2,5) 2 – 6,25 + 4 = (2х + 2,5) 2 – 2,25
Здесь мы добавили к трехчлену слагаемое 2,5 2 и тут же его отняли. Оно было необходимо для получения формулы квадрата суммы.
Отметим, что подобное свертывание можно использовать для решения квадратного уравнения. Действительно, пусть дано уравнение
4х 2 + 10х + 4 = 0
Выше мы уже преобразовали трехчлен, стоящий слева. Произведем замену:
(2х + 2,5) 2 – 2,25 = 0
Имеем уравнение, очень похожее на неполное, где отсутствует коэффициент b. Попробуем его решить аналогичным путем:
Из этой записи мы получили два линейных уравнения:
2х + 2,5 = – 1,5 или 2х + 2,5 = 1,5
Решая их, находим два корня:
2х = – 1,5 – 2,5 или 2х = 1,5 – 2,5
2х = – 4 или 2х = – 1
х = – 2 или х = – 0,5
Аналогично можно решить и любое другое полное квадратное уравнение. Однако проще пользоваться специальными формулами, в которые надо подставлять значения коэффициентов a, b, с и получать корни квадратного уравнения. Выведем эти формулы.
Пусть есть уравнение
Поделим обе части уравнения на коэффициент а:
Далее надо выделить квадрат суммы, что бы потом свернуть его по формуле сокращенного умножения:
Далее обозначим числитель в правой части (b 2 – 4ac) буквой D. Эту величину называют дискриминантом квадратного уравнения.
Перепишем уравнение с учетом этой замены:
Далее рассмотрим три случая:
- D 2 – заведомо положительное число). Слева стоит квадрат выражения, а он никак не может оказаться отрицательным. В итоге имеем, что при отрицательном дискриминанте у уравнения отсутствуют корни.
- D = 0. При таком варианте справа получается ноль:
Квадрат только одного числа равен нулю – самого нуля, поэтому
Итак, при нулевом дискриминанте у уравнения есть только один корень.
- D> 0. В этом варианте дробь справа оказывается положительным числом, а потому у нее есть два квадратных корня. Решение будет выглядеть так:
Полученное выражение называют основной формулой корней квадратного уравнения.
Если дискриминант – положительное число, то уравнение существует два корня. Для вычисления первого из них надо в формуле квадратного уравнения вместо знака ± поставить минус, а для вычисления второго – знак плюс. Часто 1-ый корень обозначают как х1, а 2-ой – как х2. Заметим, что если D = 0, то при подстановке в основную формулу будет получаться один и тот же корень независимо от выбора знака плюс или минус.
Пример. Решите уравнение
2х 2 – 5х – 3 = 0
Решение. Выпишем коэффициенты уравнения
Вычислим значение дискриминанта:
D = b 2 – 4ас = (– 5) 2 – 4•2•(– 3) = 25 + 24 = 49
Так как он больше нуля, то должно получиться два корня. Их можно найти по основной формуле квадратного уравнения:
Пример. Найдите все корни уравнения
3х 2 + 6х + 5 = 0
Решение. Найдем дискриминант:
D = b 2 – 4ас = 6 2 – 4•3•5 = 36 – 60 = – 24
Дискриминант оказался отрицательным, значит, и корней у уравнения нет.
Ответ: нет корней.
Пример. Найдите значения х, при которых выполняется равенство
4х 2 – 12х + 9 = 0
Решение. Вычислим дискриминант:
D = (– 12) 2 – 4•4•9 = 144 – 144 = 0
Так как D = 0, существует лишь один корень:
Пример. Найдите значения у, при которых справедливо равенство
2у 2 + 4у + 9 = у 2 + 11у + 3
Решение. На первый взгляд это уравнение не похоже на изучавшие до этого квадратные уравнения. Однако слагаемые, записанные справа, можно перенести влево, после чего можно будет привести подобные слагаемые:
2у 2 + 4у + 9 = у 2 + 11у + 3
2у 2 + 4у+ 9–у 2 – 11у– 3 = 0
Получили классическое квадратное уравнение, для которого можно рассчитать дискриминант:
D = b 2 – 4ас = (– 7) 2 – 4•1•6 = 49 – 24 = 25
Найдем значения двух корней:
Видео:Уравнения, сводящиеся к квадратным. Биквадратное уравнениеСкачать

Уравнения, сводящиеся к квадратным
Так как любое квадратное уравнение решается довольно легко, то другие, более сложные уравнения, часто пытаются свести к квадратным. Сначала рассмотрим так называемые биквадратные уравнения. Пусть надо решить уравнение
2х 4 –26х 2 + 72 = 0
На первый взгляд в левой части стоит полином четвертой, а не второй степени, то есть это уравнение не является квадратным. Введем переменную t, равную х 2 :
Если это выражение возвести в квадрат, то получим
t 2 = (х 2 ) 2 = х 4
Теперь заменим в исходном уравнении х 4 на t 2 , а х 2 на t:
2t 2 –26t + 72 = 0
Получили квадратное уравнение, из которого можно найти значение t. Посчитаем дискриминант:
D = (– 26) 2 – 4•2•72 = 676 – 576 = 100
Можно найти два значения t:
Однако нам надо найти значение х, а не t. Вспомним, что мы проводили замену
Подставляя вместо t найденные корни 4 и 9, получим ещё два уравнения:
Первое имеет корни (– 2) и 2, а второе (– 3) и 3. Все эти 4 числа являются корнями исходного уравнения
2х 4 – 26х 2 + 72 = 0
Уравнения, которые можно свести к квадратному заменой переменных t = x 2 , называют биквадратными уравнениями.
Мы рассмотрели пример, в котором биквадратное уравнение имело 4 корня. Однако порою их может быть и меньше.
Пример. Укажите все корни уравнения
у 4 + 4у 2 – 5 = 0
Решение. Данное уравнение подходит под определение биквадратного, а потому произведем замену t = y 2 :
D = 4 2 – 4•1•(– 5) = 16 – (– 20) = 36
далее проводим обратную замену и получаем уравнения:
Первое из них не имеет решения, ведь квадрат числа – это неотрицательное число. Поэтому решать придется только второе уравнение:
Подстановка t = x 2 самая простая и очевидная, однако, порою нужно выполнять более сложные подстановки.
Пример. Найдите все z, для которых выполняется условие
(z – 2)(z – 3)(z – 4)(z – 5) = 24
Решение.Замена неочевидна, и всё же попробуем такой вариант:
Тогда содержимое каждой скобки примет вид:
z– 2 = z– 3,5 + 1,5 = t + 1,5
z– 3 = z– 3,5 + 0,5 = t + 0,5
z– 4 = z– 3,5 – 0,5 = t–0,5
z– 5 = z – 3,5 – 1,5 = t–1,5
Уравнение примет вид:
(t + 1,5)(t + 0,5)(t – 0,5)(t – 1,5) = 24
Поменяем местами скобки:
(t – 0,5)(t + 0,5)(t – 1,5)(t + 1,5) = 24
Можно заметить, что в соседние скобки можно переписать, используя формулу разности квадратов:
(t 2 – 0,5 2 )(t 2 – 1,5 2 ) = 24
Для удобства произведем ещё одну замену s = t 2 :
(s– 0,5 2 )(s– 1,5 2 ) = 24
Раскроем скобки в левой части:
s 2 – 2,25s– 0,25s + 0,5625 = 24
s 2 – 2,5s + 0,5625– 24 = 0
s 2 – 2,5s– 23,4375 = 0
Получили классическое квадратное уравнение, которое решается через дискриминант:
D = (– 2,5) 2 – 4•1•(– 23,4375) = 6,25 + 93,75 = 100
Произведем 1-ую обратную замену t 2 = s:
Первое уравнение решений не имеет, а у второго ровно 2 корня:
Пришло время второй замены z– 3,5 = t, из которой получаем два уравнения:
z– 3,5 = – 2,5 или z– 3,5 = 2,5
z= – 2,5 + 3,5 или z= 2,5 + 3,5
Видео:Решение уравнений, сводящихся к квадратным. §23 алгебра 8 классСкачать

Задачи, решаемые с помощью квадратных уравнений
При рассмотрении задач, связанных с геометрией, свойствами чисел, движением тел, очень часто возникают квадратные уравнения.
Пример. Площадь прямоугольника составляет 126 см 2 , а одна из его сторон на 5 см длиннее другой. Каковы длины сторон этого прямоугольника?
Решение. Обозначим как k длину той стороны прямоугольника, которая меньше. Тогда протяженность второй стороны будет равна k + 5 см. Площадь прямоугольника – это произведение его сторон, а потому можно записать:
Решим это уравнение:
k 2 + 5k – 126 = 0
D = 5 2 – 4•1•(– 126) = 25 + 504 = 529
Первый корень равен (– 14). Однако ясно, что длина стороны прямоугольника не может измеряться отрицательным числом, поэтому этот корень надо отбросить. Остается только k = 9. То есть длина первой стороны равна 9 см. Вторая сторона равна k + 5, то есть 9 + 5 = 14 см.
Ответ: 9 и 14 см.
Пример. Сумма квадратов двух последовательных нечетных чисел составляет 290. Что это за числа?
Решение. Обозначим первое число как n. Нечетные числа чередуются с четными, поэтому следующим нечетным числом будет n + 2. Перепишем условие задачи в виде уравнения и найдем его корни:
n 2 + (n + 2) 2 = 290
n 2 + n 2 + 4n + 4 – 290 = 0
2n 2 + 4n – 286 = 0
D = 4 2 – 4•2•(– 286) = 16 + 2288 = 2304
Получили два решения. Если первое число равно – 13, то второе составит n + 2 = – 11. Если же n = 11, то второе число будет равно 13.
Ответ: – 13 и 11, либо 11 и 13.
Видео:Алгебра 8. Решение уравнений, сводящихся к квадратнымСкачать

Теорема Виета
Большое значения имеют уравнения, у которых старшим коэффициентом является единица. Математики называют их приведенными уравнениями.
Дадим несколько примеров приведенных квадратных уравнений:
- х 2 + 6х + 29 = 0
- у 2 – 7,54у + 87 = 0
- z 2 + 21z + 112 = 0
Название «приведенное» возникло из-за того, что каждое квадратное уравнение можно сделать приведенным, если поделить его части на коэффициент перед х 2 . Пусть есть уравнение
Поделим на 4 обе его части:
х 2 + 1,25х + 1,5 = 0
Для приведенного уравнения сформулирована теорема Виета, которая указывает на взаимосвязь его корней и коэффициентов:
Доказать это очень легко. Если у уравнения
существует два корня, то они вычисляются по формулам:
Найдем их сумму:
Аналогично можно посчитать и их произведение:
Естественно, если у уравнения не существует корней (D 2 – 8х + 15 = 0; корни (х1 и х2) равны 3 и 5, в чем можно убедиться подстановкой:
Перемножим корни и получим 3•5 = 15 (свободный член), при сложении корней получается 3 + 5 = 8 (второй коэффициент без минуса);
- у 2 + 13у + 42= 0, корни (– 6) и (– 7), произведение корней 42, сумма корней – 13;
- х 2 + 2х – 8 = 0, корни (– 4) и 2, их сумма равна (– 2), а произведение (– 8).
Справедливо и утверждение, известное как обратная теорема Виета:
Возьмем числа 4 и 9. Их сумма равна 13, а произведение 36, поэтому они являются корнями уравнения:
х 2 – 13х + 36 = 0
в чем можно убедиться, подставив их вместо х.
Пример. Учитель математики перед уроком составляет квадратные уравнения, причем стремится к тому, чтобы у них были целые корни (чтобы детям было просто считать). Подскажите ему пример уравнения, чьи корни равны 3 и 8.
Решение. Перемножим и сложим числа 3 и 8:
Соответственно, уравнением с корнями 3 и 8 будет
х 2 – 11х + 24 = 0
Ответ: х 2 – 11х + 24 = 0
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Разложение квадратного трехчлена на множители
При решении уравнения
мы находим его корни. Однако отдельно выделяют и такое понятие, как корень многочлена. Так называют значение переменной, которая обращает полином в ноль.
Понятно, что для нахождения корней полинома второй степени следует решить квадратное уравнение.
Сначала рассмотрим трехчлены, у которых коэффициент при х 2 а равен 1. Предположим, что нам удалось разложить его на произведение двух линейных полиномов:
х 2 + bх + с = (х –s)(х –k)
где s и k– какие-то произвольные числа.
Выражение справа является произведением, а потому обращается в ноль только тогда, когда нулю равен один из множителей:
х – s = 0 или х – k = 0
Так как при х = s или х = k в ноль обращается правая часть тождества, то также должна обращаться и левая часть. Получается, что числа s и k – это корни трехчлена х 2 + bх + с.
Убедимся в этом, раскрыв скобки в правой части тождества:
(х –s)(х –k) = х 2 –kx–sx + sk = х 2 – (k + s)х + sk
подставим это выражение в исходное равенство:
х 2 + bх + с = (х – s)(х — k) = х 2 – (k + s)х + sk
х 2 + bх + с = х 2 – (k + s)х + sk
Получается, произведение s и k дает свободный член, а их сумма в точности равна коэффициенту при х, взятому со знаком минус. Значит, по теореме Виета, они являются корнями уравнения!
Обозначим корни уравнения как х1 и х2. Если у трехчлена коэффициент а отличен от единицы, то эта формула (ее называют формулой разложения квадратного трехчлена на множители) примет несколько иной вид:
То есть справедливо утверждение:
А теперь и докажем его.
Пусть есть уравнение ах 2 + bx + c = 0 с корнями х1 и х2. Поделим его на а:
х 2 + (b/a)х + с/а = 0
по теореме Виета можно записать:
Умножив первое тождество на (– а), а второе наа, получим
Осталось подставить эти равенства в исходный многочлен:
Для чего же мы доказывали эту теорему? С ее помощью можно выполнить разложение квадратного трехчлена на множители. Проиллюстрируем это на примерах.
Пример. Разложите полином
2х 2 + 12х – 14
на множители.
Решение. Для начала следует решить уравнение 2х 2 + 12х – 14 = 0:
D = 12 2 – 4•2•(– 14) = 144 + 112 = 256
Найдя х1 и х2, можем выполнить и разложение:
2х 2 + 12х – 14 = 2(х – 1)(х – (– 7)) = 2(х – 1)(х + 7)
Ответ: 2(х – 1)(х + 7)
Пример. Упростите выражение
Решение. На первый взгляд кажется, что сокращать нечего. Однако и в числителе, и в знаменателе находятся квадратные трехчлены. Разложим их на множители, решив соответствующие уравнения:
D = 2 2 – 4•1•(– 15) = 4 + 60 = 64
h 2 – 2h– 15 = (h+ 5)(h– 3)
Теперь раскладываем второй полином:
D = (– 9) 2 – 4•1•18 = 81 – 72 = 9
Соответственно, можно записать:
h 2 – 9h +18 = (h– 3)(h– 6)
А теперь подставим в исходную дробь полученные выражения:
Отметим, что если у полинома второй степени нет корней, то и разложить его на множители не получится.
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Дробно-рациональные уравнения
Периодически приходится сталкиваться с уравнениями, где переменные присутствуют в знаменателе какой-нибудь дроби. Их называют дробно-рациональными уравнениями. Обычно их можно свести к более простому виду, но при этом следует учитывать ту особенность, что корень уравнения не должен обращать знаменатель в ноль.
Пример. Найдите решение дробно-рационального уравнения
Решение. Для начала перенесем дробь из правой части в левую, а потом приведем дроби к общему знаменателю:
Умножим уравнение на величину (х – 2)(х + 3)
(х + 1)(х – 2) + 10х – 4(х + 3) = 0
х 2 – 2х + х – 2 + 10х – 4х – 12 = 0
D = 5 2 – 4•1•(– 14) = 25 + 56 = 81
Казалось бы, мы нашли два корня: 2 и (– 7). Однако в исходном уравнении в знаменателе стоит выражение (х – 2)(х – 3). При х = 2 оно обращается в нуль, то есть дробь потеряет смысл. Поэтому корень 2 следует отбросить, и остается лишь корень (– 7)
Видео:Тема 13. Решение целых рациональных уравнений, сводящихся к квадратным уравнениямСкачать

Решение уравнений, сводящихся к квадратным
Биквадратные уравнения
Биквадратным уравнением называется уравнение вида:
$$ ax^4+bx^2+c = 0, a neq 0 $$
Алгоритм решения биквадратного уравнения
Шаг 1. Ввести новую переменную: $z = x^2 ge 0$.
Переписать уравнение для новой переменной: $az^2+bz+c = 0$
Шаг 2. Решить полученное квадратное уравнение.
Если $D gt 0$, $z_ = frac<-b pm sqrt> $. Проверить условие $z ≥ 0$, если положительных корней нет, решений нет, переход на шаг 4.
Если D = 0,$z_0 = -frac$. Проверить условие $z ge 0$, если корень отрицательный, решений нет, переход на шаг 4.
Если $D lt 0$, решений нет, переход на шаг 4.
Шаг 3.Если после шага 2 остались положительные корни, найти x: $x = pm sqrt$.
Шаг 4. Работа завершена.
Шаг 1. $z = x^2 ge 0, z^2+7z-30 = 0$
$z_1 = -10 lt 0, z_2 = 3 gt 0 $
Шаг 3. Находим корни из положительного $z: x_ = pm sqrt$
Метод разложения на множители
Решение уравнений, в которые переменная x входит с различными натуральными степенями и вещественными коэффициентами, по существу, является поиском корней многочлена.
Число $x_0$ называют корнем многочлена $P_n (x) = a_n x^n+a_ x^ + ⋯ + a_1 x+a_0$ если $P_n (x_0 ) = 0$.
Для многочлена $P_n$ (x) произвольной степени n справедливо следующее.
Если $x = x_0$ является корнем многочлена $P_n$ (x), то $P_n (x) = (x-x_0) P_ (x)$, где $P_ (x)$ — многочлен степени n-1.
Таким образом, разными способами находя корни и формируя скобки, можно постепенно добиваться понижения степени «оставшегося» многочлена, пока не будут найдены все корни.
При разложении многочлена
- множители вида (x-a) называют линейными множителями ;
- множители вида $ (x^2+bx+c)$, для которых $D lt 0$, называют неприводимыми квадратичными множителями .
Любой многочлен $P_n$ (x) можно представить в виде конечного числа линейных и/или неприводимых квадратичных множителей.
Причём, такое представление единственно с точностью до порядка множителей.
Для разложения многочленов на множители применяются разные методы:
- вынесение общего множителя за скобку (см. §19 справочника для 7 класса);
- группировка (см. §20 справочника для 7 класса);
- формулы сокращенного умножения (см. §25 справочника для 7 класса);
- метод неопределённых коэффициентов;
- выделение полного квадрата и т.п.
Решим уравнение $2x^3-x^2-8x+4 = 0$.
Раскладываем на множители: $x^2 (2x-1)-4(2x-1) = 0$
$$ (x^2-4)(2x-1) = 0 Rightarrow (x-2)(x+2)(2x-1) = 0 $$
Корни уравнения: $x_1 = 2, x_2 = -2, x_3 = frac$
Метод замены переменной
Замена переменной – это уравнение, с помощью которого можно упростить исходное уравнение, и перейти к решению системы из двух более простых уравнений:
$Исходное quad сложное quad уравнение iff <left< begin Новая quad переменная quad (урав. quad связи quad со quad старой quad переменной \ Исходное quad урав. quad в quad «упрощ.» quad виде end right.>$
Например, для биквадратных уравнений:
$$ ax^4+bx^2+c = 0 iff <left< begin z = x^2 ge 0 \ az^2+bz+c = 0 end right.> $$
Можно предложить аналогичные схемы для других уравнений:
$$ ax+b sqrt+c = 0 iff <left< begin z = sqrt ge 0 \ az^2+bz+c = 0 end right.> $$
И, в общем виде, для любой рациональной степени n:
$$ ax^+bx^n+c = 0 iff <left< begin z = x^n \ az^2+bz+c = 0 end right.> , n in Bbb Q $$
В других случаях замена переменной не настолько очевидна.
Но при удачном выборе, этот метод очень упрощает задачу.
Раскроем скобки:$ x^2-x = frac$. Сделаем замену:
$$ z = frac Rightarrow z(z-2) = 24 Rightarrow z^2-2z-24 = 0 Rightarrow (z-6)(z+4) = 0 Rightarrow left[ begin z_1 = -4 \ z_2 = 6 end right.$$
Возвращаемся к исходной переменной x:
$$ left[ begin x^2-x = -4 \ x^2-x = 6 end right. Rightarrow left[ begin x^2-x+4 = 0 \ x^2-x-6 = 0 end right. Rightarrow left[ begin D lt 0, x in varnothing \ (x-3)(x+2) = 0 end right. Rightarrow left[ begin x_1 = -2 \ x_2 = 3 end right. $$
При использовании метода замены переменной не забывайте возвращаться к исходной переменной.
Выделение полного квадрата
Метод выделения полного квадрата является одним из методов разложения на множители. Его идея – представить многочлен в виде разности квадратов двух других многочленов степенью пониже, и разложить разность на две скобки:
$$ P_n (x) = Q_k^2 (x)-R_m^2 (x) = (Q_k (x)-R_m (x))(Q_k (x)+R_m (x)) $$
Такое разложение не всегда возможно.
Рассмотрим выделение полного квадрата для квадратного трёхчлена:
$$ = a Biggl(x+frac Biggr)^2 — frac = a Biggl(x+ frac Biggr)^2- frac, D = b^2-4ac $$
Нами выделен полный квадрат $(x+frac)^2$.
Данное выражение используется для построения и анализа графиков парабол (см. §28 данного справочника).
А его разложение на две линейные скобки, известное как теорема Виета (см. §26 данного справочника), возможно только при условии $D ge 0$.
Решить уравнение $x^4+4x^2-1 = 0$
Выделим полный квадрат и разложим на множители:
$$ left[ begin x^2+2-sqrt = 0 \ x^2+2+sqrt = 0 end right. Rightarrow left[ begin x^2 = sqrt -2 gt 0 \ x^2 = -(2+sqrt) lt 0 end right. Rightarrow x_1,2 = pm sqrt<sqrt-2> $$
Примеры
Пример 1. Решите биквадратные уравнения:
Делаем замену: $2x^4+7x^2-4 = 0 iff <left< begin z = x^2 ge 0 \ 2z^2+7z-4 = 0 end right.>$
Решаем квадратное уравнение: $D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2$
$$ z = frac = left[ begin z_1 = -4 lt 0 \ z_2 = frac gt 0 end right. $$
Выбираем положительный z и возвращаемся к исходной переменной x:
Делаем замену: $(x+3)^4-10(x+3)^2+24 = 0 iff <left< begin z = (x+3)^2 ge 0 \ z^2-10z+24 = 0 end right.>$
Решаем квадратное уравнение: $z^2-10z+24 = 0 Rightarrow (z-4)(z-6) = 0 Rightarrow left[ begin z_1 = 4 \ z_2 = 6 end right.$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin (x+3)^2 = 4 \ (x+3)^2 = 6 end right. Rightarrow left[ begin x+3 = pm sqrt \ x+3 = pm sqrt end right. Rightarrow left[ begin x_ = -3 pm 2 \ x_ = -3 pm sqrt end right. Rightarrow left[ begin x_1 = -5 \ x_2 = -1 \ x_ = -3 pm sqrt end right. $$
Пример 2. Решите уравнения аналогичные биквадратным:
Делаем замену: $x+4 sqrt-60 = 0 iff <left< begin z = sqrt ge 0 \ z^2+4z-60 = 0 end right.>$
Решаем квадратное уравнение: $ z^2+4z-60 = 0 Rightarrow (z+10)(z-6) = 0 Rightarrow left[ begin z_1 = -10 \ z_2 = 6 end right.$
Выбираем положительный корень и возвращаемся к исходной переменной:
Делаем замену: $(x-1)^6-7(x-1)^3-8 = 0 iff <left< begin z = (x-1)^3 \ z^2-7z-8 = 0 end right.>$
Решаем квадратное уравнение: $ z^2-7z-8 = 0 Rightarrow (z+1)(z-8) = 0 Rightarrow left[ begin z_1 = -1 \ z_2 = 8 end right.$
При замене куба знак z может быть любым, берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin (x-1)^3 = -1 \ (x-1)^3 = 8 end right. Rightarrow left[ begin x-1 = -1 \ x-1 = 2 end right. Rightarrow left[ begin x_1 = 0 \ x_2 = 3 end right. $$
Пример 3. Решите уравнения с помощью замены переменной:
Заметим, что $(x+3)^2 = x^2+6x+9$. Получаем:
$$ (x^2+6x)^2-(x^2+6x+9) = 33 Rightarrow (x^2+6x)^2-(x^2+6x)-42 = 0 $$
Решаем квадратное уравнение: $ z^2-z-42 = 0 Rightarrow (z+6)(z-7) = 0 Rightarrow left[ begin z_1 = -6 \ z_2 = 7 end right.$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin x^2+6x = -6 \ x^2+6x = 7 end right. Rightarrow left[ begin x^2+6x+6 = 0 \ x^2+6x-7=0 end right. Rightarrow left[ begin D = 12, x = frac<-6 pm 2 sqrt> \ (x+7)(x-1) = 0 end right. Rightarrow left[ begin x_ = -3 pm sqrt \ x_3 = -7 \ x_4 = 1 end right. $$
Делаем замену: $ frac + frac = 2 iff left[ begin z = x^2+3 ge 3 \ frac + frac = 2 end right.$
Решаем уравнение относительно z:
$$ frac + frac = 2 Rightarrow frac = frac Rightarrow 4(z+1)+5z = 2z(z+1) $$
$$ 2z^2+2z-9z-4 = 0 Rightarrow 2z^2-7z-4 = 0 $$
$$ D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2 $$
$$ z = frac = left[ begin z_1 = — frac lt 3 \ z_2 = 4 gt 3 end right. $$
Выбираем корень больше 3 и возвращаемся к исходной переменной:
$$ x^2+3 = 4 Rightarrow x^2 = 1 Rightarrow x_ = pm 1$$
Пример 4*. Решите уравнения:
Приведём это уравнение к биквадратному.
В линейных множителях (x+a) выберем все a =
Найдем их среднее арифметическое (см. §52 справочника для 7 класса)
Замена переменных $z = x+a_$:
Упрощаем уравнение, используя формулу разности квадратов:
$$ (z^2-9)(z^2-1) = 945 Rightarrow z^4-10z^2+9 = 945 Rightarrow z^4-10z^2-936 = 0 $$
Получили биквадратное уравнение.
Делаем замену: $z^4-10z^2-936 = 0 iff <left< begin t = z^2 ge 0 \ t^2-10t-936 = 0 end right.> $
Решаем квадратное уравнение:
$$ D = 100+4 cdot 936 = 3844 = 62^2, t = frac = left[ begin t_1 = -26 lt 0 \ t_2 = 36 gt 0 end right. $$
Выбираем положительный корень и возвращаемся к переменной z:
$$ z = pm sqrt = pm sqrt = pm 6 $$
Возвращаемся к исходной переменной x:
$$ x = z-4 = pm 6-4 = left[ begin x_1 = -10 \ x_2 = 2 end right. $$
$$ z- frac =2,1 |times z (z neq 0) $$
$$ z^2-2,1z-1 = 0 Rightarrow D = 2,1^2+4 = 8,41 = 2,9^2; z = frac = left[ begin z_1 = -0,4 \ z_2 = 2,5 end right. $$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin frac = -0,4 \ frac = 2,5 end right. Rightarrow left[ begin x^2+1 = -0,4x \x^2+1 = 2,5x end right. Rightarrow left[ begin x^2+0,4x+1 = 0 \ x^2-2,5x+1 = 0 end right. $$
В первом уравнении $D = 0,4^2-4 lt 0$, решений нет.
Во втором уравнении (x-2)(x-1/2) = 0 $Rightarrow left[ begin x_1 = frac \ x_2 = 2 end right.$
💡 Видео
Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

9 класс. Алгебра. Уравнения, сводящиеся к квадратнымСкачать

Алгебра 10 класс Уравнения,сводящиеся к квадратнымСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Решение уравнений, сводящихся к квадратным уравнениям биквадратное уравнение (урок 1)Скачать

Решение уравнений, сводящихся к квадратным уравнениям (урок 4)Скачать