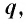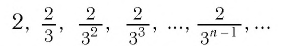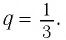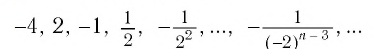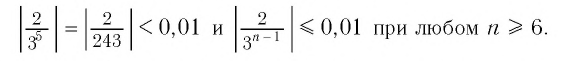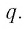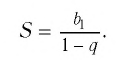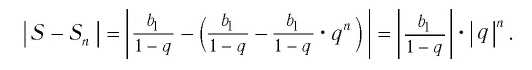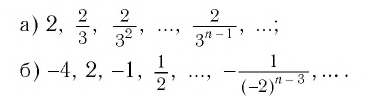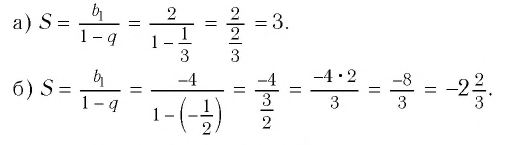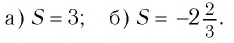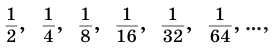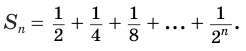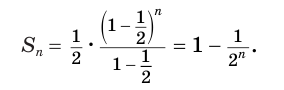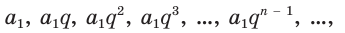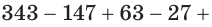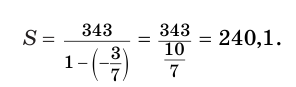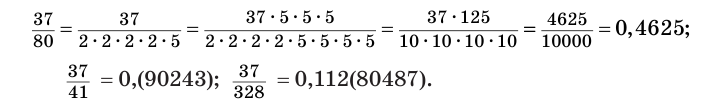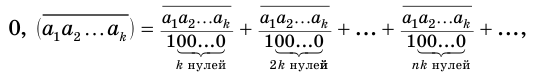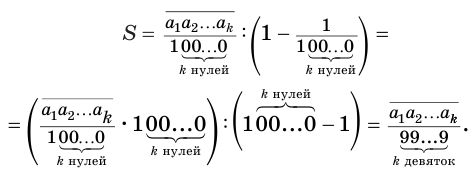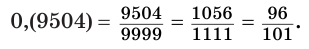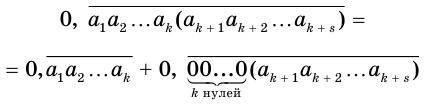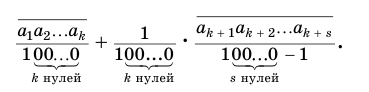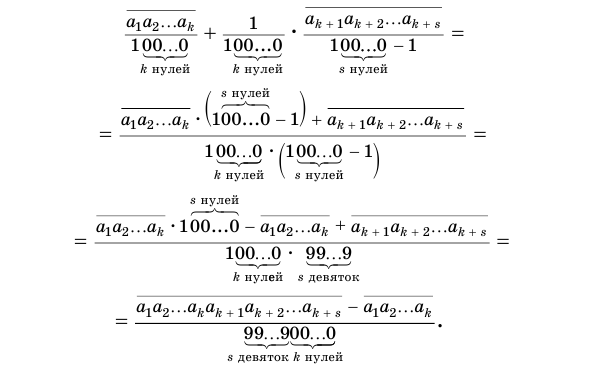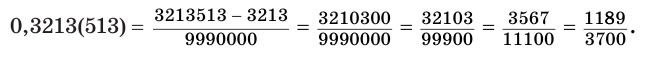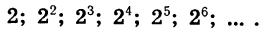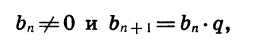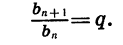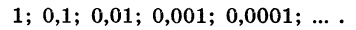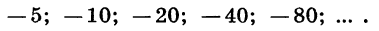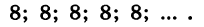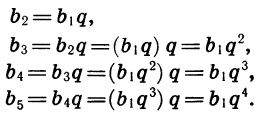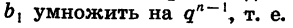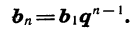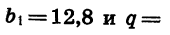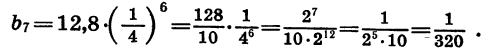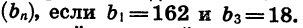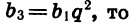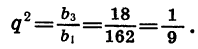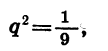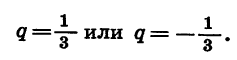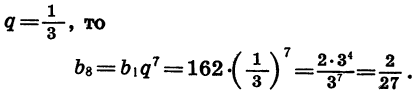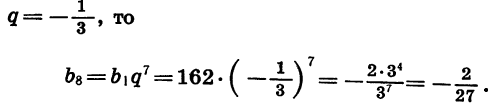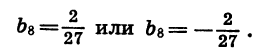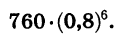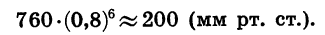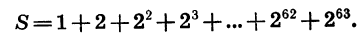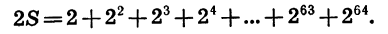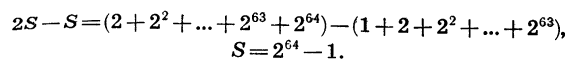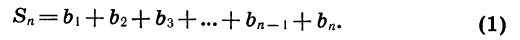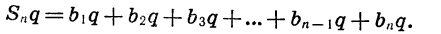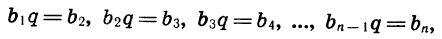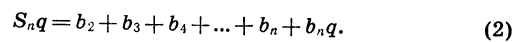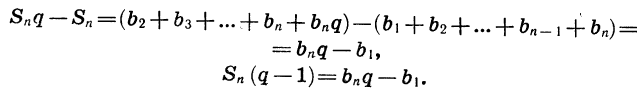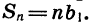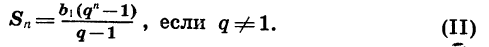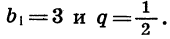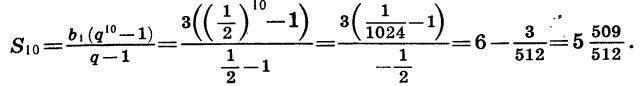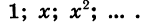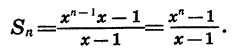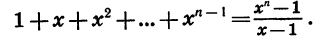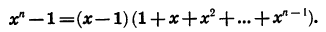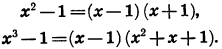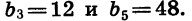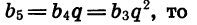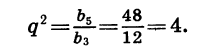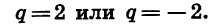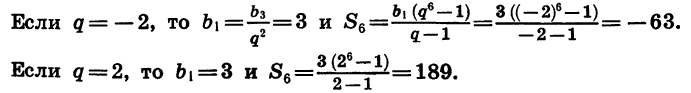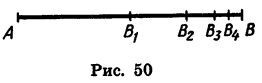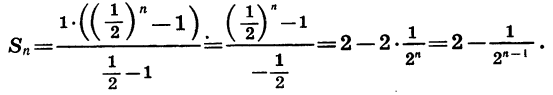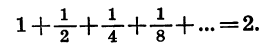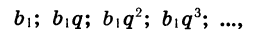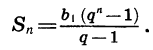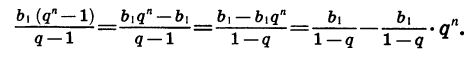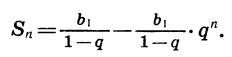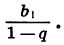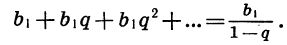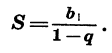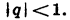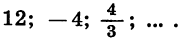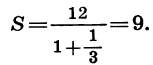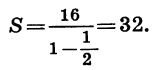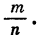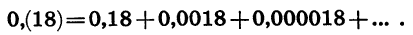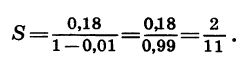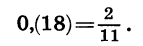Решение уравнений сумма бесконечной геометрической прогрессии

Содержание:

Определение:

Геометрическая прогрессия со знаменателем

Видео:9 класс - Алгебра - Сумма бесконечной геометрической прогрессииСкачать

Примеры бесконечно убывающих геометрических прогрессий

Приведем примеры бесконечно убывающих геометрических прогрессий.

Пример №1

является бесконечно убывающей геометрической прогрессией с

первым членом 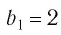и знаменателем

Пример №2

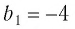
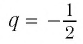
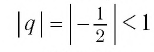
является бесконечно убывающей геометрической прогрессией с первым членом и знаменателем (здесь ). Изобразим четыре первых члена геометрической прогрессии из примера 1 на координатной прямой (рис. 1).

Мы видим, что чем больше номер прогрессии, тем ближе этот член к нулю, т.е. тем меньше его модуль, и с увеличением 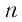этот модуль становится меньше любого заданного положительного числа.

Например, если мы зададим число 0,01, то

Изобразим 6 первых членов геометрической прогрессии из примера 2 на координатной прямой (рис. 2).

И в этом примере мы видим, что чем больше номер члена прогрессии, тем ближе этот член к нулю, т. е. тем меньше его модуль, и с увеличением п этот модуль становится меньше любого заданного положительного числа.

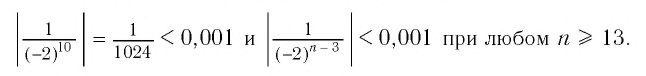
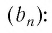
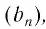
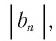
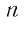
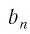
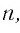
Например, если мы зададим число 0,001, то Такую же картину, как и в этих двух примерах, мы наблюдаем в любой бесконечно убывающей геометрической прогрессии чем больше номер п члена прогрессии тем меньше и с увеличением этот, модуль становится меньше любого заданного положительного числа. Это утверждение формулируется еще и так:

стремится к нулю при стремящемся к бесконечности.

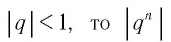
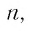
Заметим, что если стремится к нулю при стремящемся к бесконечности.

Рассмотрим бесконечно убывающую геометрическую прогрессию с первым членом 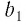и знаменателем

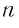
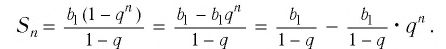
Запишем формулу суммы первых членов этой прогрессии и преобразуем это выражение: Обозначим

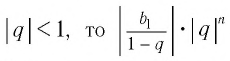
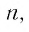
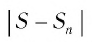
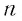
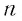
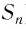
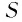
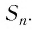
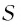
Так как стремится к нулю при стремящемся к бесконечности. Значит, стремится к нулю при , стремящемся к бесконечности, т. е. чем больше число (чем больше слагаемых в сумме ), тем меньше разница между и Поэтому число называют суммой бесконечно убывающей геометрической прогрессии.

Пример №3

Найти сумму бесконечно убывающей геометрической прогрессии:

Решение:

Ответ:

Видео:Бесконечно убывающая геометрическая прогрессия. 9 класс.Скачать

Всё о бесконечно убывающей геометрической прогрессии

Пример:

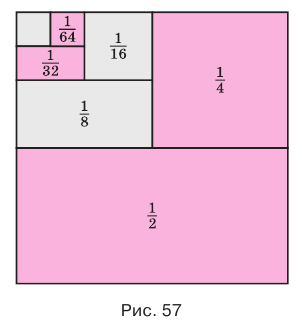
Рассмотрим квадрат со стороной 1 (рис. 57). Если середины его противоположных сторон соединить отрезком, то возникнут два прямоугольника с площадью .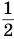

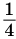
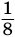
Если теперь середины одного из полученных прямоугольников соединить отрезком, то получится два прямоугольника с площадью . Снова повторив такое действие, получим два прямоугольника с площадью . Будем продолжать этот процесс далее. В результате получим бесконечную убывающую последовательность

у которой каждый следующий член получается из предыдущего умножением на .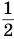

Естественно считать, что сумма 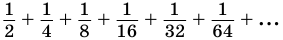равна 1, так как она представляет площадь всего данного квадрата.

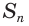
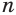
Записанная сумма содержит бесконечно много слагаемых. Рассмотрим ее часть из слагаемых:

Ее компоненты образуют геометрическую прогрессию со знаменателем 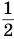. Поэтому

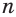
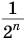
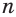
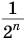
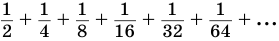
С возрастанием значения переменной значение выражения становится все меньше и меньше: значение переменной всегда можно подобрать так, что значение выражения станет меньше любого малого заранее выбранного числа. Поэтому бесконечную сумму считают равной 1.

Рассмотрим теперь бесконечную геометрическую прогрессию

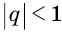
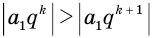
где . Для таких прогрессий истинно условие , их называют бесконечно убывающими геометрическими прогрессиями.

Сумма бесконечно убывающей геометрической прогрессии

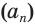
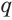
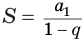
Суммой членов бесконечно убывающей геометрической прогрессии со знаменателем называется число .

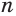
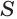
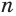
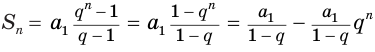
Это определение объясняется тем, что с увеличением число все меньше отличается от суммы первых членов этой прогрессии. Действительно,

.

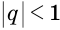
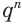
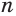
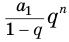
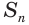
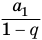
Поскольку , то с увеличением приближается к нулю, а значит, приближается к нулю и вычитаемое . Поэтому сумма приближается к .

Пример №4

Найдем значение суммы

.

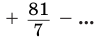
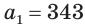
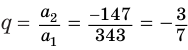
Замечаем, что слагаемые этой алгебраической суммы являются членами бесконечно убывающей геометрической прогрессии, у которой и . Поэтому

Мы знаем, что любое рациональное число можно представить десятичной дробью. При этом если разложение на простые множители знаменателя несократимой дроби, представляющей данное рациональное число, содержит только двойки и пятерки, то получается конечная десятичная дробь, а если это разложение содержит хотя бы один простой множитель, отличный от 2 и 5, то получается бесконечная периодическая десятичная дробь. Например:

Повторяющаяся группа цифр называется периодом десятичной дроби, группа цифр между целой частью и периодом называется предпериодом. В записи 0,112(80487) предпериод равен 112, а период — 80 487.

Обыкновенную дробь можно преобразовать в десятичную делением ее числителя на знаменатель. Установим алгоритмы преобразования бесконечной периодической десятичной дроби в обыкновенную.

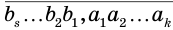
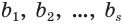
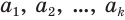
В дальнейшем мы будем пользоваться записью вида . Она обозначает десятичную дробь, целая часть которой записана с помощью цифр , а дробная — с помощью цифр .

Теорема 7.

Бесконечная периодическая десятичная дробь без предпериода равна обыкновенной дроби, числитель которой есть число, записанное цифрами периода, а знаменатель — число, записанное столькими девятками, сколько есть цифр в периоде.

Доказательство:

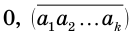
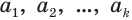
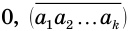
Пусть — периодическая десятичная дробь, где — цифры периода. Тогда число можно представить бесконечной суммой:

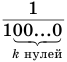
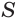
в которой каждое слагаемое получается из предыдущего умножением на . Это означает, что бесконечную периодическую дробь можно рассматривать как сумму членов бесконечно убывающей геометрической прогрессии с первым

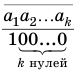
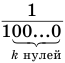
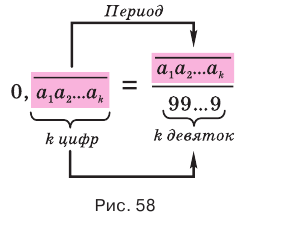
членом и знаменателем . Поэтому

Теорема 7 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби без предпериода, который изображен схемой, приведенной на рисунке 58.

Пример №5

Представим обыкновенной дробью десятичную дробь 0,(9504). Имеем:

Теорема 8.

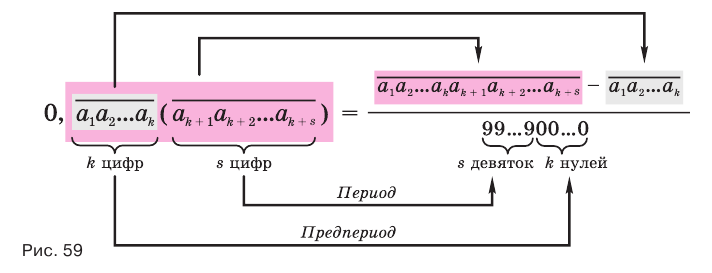
Бесконечная десятичная периодическая дробь с предпериодом равна обыкновенной дроби, числитель которой равен разности между числом, записанным цифрами от десятичной запятой до конца первого периода, и числом, записанным цифрами предпериода, а знаменатель — числу, записанному столькими девятками, сколько есть цифр в периоде, и столькими нулями, сколько есть цифр в предпериоде.

Доказательство:

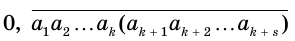
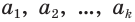
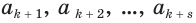
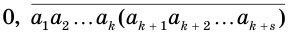
Пусть — периодическая десятичная дробь, где — цифры предпериода, — цифры периода. Тогда число можно представить суммой

или, с учетом теоремы 7, суммой

Преобразуем полученное выражение:

Теорема 8 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби с предпериодом, который отражен на схеме, представленной на рисунке 59.

Пример №5

Представим обыкновенной дробью десятичную дробь 0,3213(513). Имеем:

• Периодические дроби
• Степень с рациональным показателем
• Степень с действительным показателем
• Логарифм — формулы, свойства и примеры
• Корень n-й степени
• Тождества с корнями, содержащие одну переменную
• Действия с корнями нечетной степени
• Действия с корнями четной степени

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Как за 10 минут понять СЛОЖНЕЙШУЮ ТЕМУ в Алгебре? Геометрическая прогрессияСкачать

Геометрическая прогрессия в математике с примерами решения и образцами выполнения

Определение геометрической прогрессии:

Рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями:

Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером геометрической прогрессии.

Определение:

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Иначе говоря, последовательность 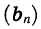— геометрическая прогрессия, если для любого натурального п выполняются условия

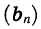
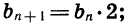
где q — некоторое число. Обозначим, например, через последовательность натуральных степеней числа 2. В этом случае для любого натурального п верно равенство здесь q = 2.

Из определения геометрической прогрессии следует, что отношение любого ее члена, начиная со второго, к предыдущему члену равно q, т. е. при любом натуральном n верно равенство

Число q называют знаменателем геометрической прогрессии.

Очевидно, что знаменатель геометрической прогрессии отличен от нуля.

Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель.

Если 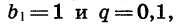то получим геометрическую прогрессию

Условиями 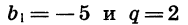задается геометрическая прогрессия

Если 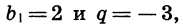то имеем прогрессию

Если 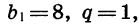то получим геометрическую прогрессию

Зная первый член и знаменатель геометрической прогрессии, можно найти последовательно второй, третий и вообще любой ее член:

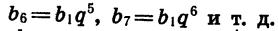
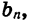
Точно так же находим, что Вообще, чтобы найти мы должны

Мы получили формулу n-го члена геометрической прогрессии.

Приведем примеры решения задач с использованием этой формулы.

Пример:

В геометрической прогрессии 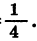Найдем b7.

По формуле n-го члена геометрической прогрессии

Пример:

Найдем восьмой член геометрической прогрессии

Зная первый и третий члены геометрической прогрессии, можно найти ее знаменатель. Так как

Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.

Задача имеет два решения:

Пример:

После каждого движения поршня разрежающего насоса из сосуда удаляется 20% находящегося в нем воздуха. Определим давление воздуха внутри сосуда, после шести движений поршня, если первоначально давление было 760 мм рт. ст.

Так как после каждого движения поршня из сосуда удаляется 20% имевшегося воздуха, то остается 80% воздуха. Чтобы узнать давление воздуха в сосуде после очередного движения поршня, нужно давление после предыдущего движения поршня умножить на 0,8.

Мы имеем геометрическую прогрессию, первый член которой равен 760, а знаменатель равен 0,8. Число, выражающее давление воздуха в сосуде (в мм рт. ст.) после шести движений поршня, является седьмым членом этой прогрессии. Оно равно

Произведя вычисления, получим:

Видео:Арифметическая и геометрическая прогрессия | Математика TutorOnlineСкачать

Формула суммы n первых членов геометрической прогрессии

Древняя индийская легенда рассказывает, что изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую — в 2 раза больше, т. е. 2 зерна, на третью — еще в 2 раза больше, т. е. 4 зерна, и т. д. до 64-й клетки. Сколько зерен должен был получить изобретатель шахмат?

Число зерен, о которых идет речь, является суммой шестидесяти четырех членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:

Умножим обе части записанного равенства на знаменатель прогрессии, получим:

Вычтем почленно из второго равенства первое и проведем упрощения:

Можно подсчитать, что масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.

Выведем теперь формулу суммы n первых членов произвольной геометрической прогрессии. Воспользуемся тем же приемом, с помощью которого была вычислена сумма S.

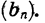
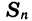
Пусть дана геометрическая прогрессия Обозначим сумму n первых ее членов через :

Умножим обе части этого равенства на q:

Вычтем почленно из равенства (2) равенство (1) и приведем подобные члены:

Отсюда следует, что при

Мы получили формулу суммы n первых членов геометрической прогрессии, в которой 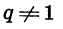. Если q = 1, то все члены прогрессии равны первому члену и

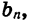
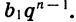
При решении многих задач удобно пользоваться формулой суммы п первых членов геометрической прогрессии, записанной в другом виде. Подставим в формулу (I) вместо выражение Получим:

Пример:

Найдем сумму первых десяти членов геометрической прогрессии 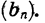в которой

Так как известны первый член и знаменатель прогрессии, то удобно воспользоваться формулой (II). Получим:

Пример:

Найдем сумму 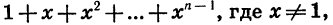слагаемые которой являются последовательными членами геометрической прогрессии

Первый член прогрессии равен 1, а знаменатель равен х. Так как 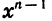является членом этой прогрессии с номером n, то задача состоит в нахождении суммы п первых ее членов. Воспользуемся формулой (I):

Таким образом, если 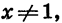то

Умножив левую и правую части последнего равенства на х — 1, получим тождество

В частности, при n = 2 и n = 3 приходим к известным формулам

Пример:

Найдем сумму шести первых членов геометрической прогрессии 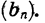если известно, что

Зная 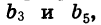можно найти знаменатель прогрессии q. Так как

Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.

Видео:9 класс, 24 урок, Геометрическая прогрессияСкачать

Сумма бесконечной геометрической прогрессии при |q|

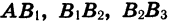
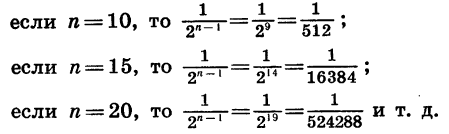
Пусть длина отрезка АВ равна 2 ед. (рис. 50). Отметим точку В1 — середину отрезка А В, затем точку В2 — середину правой его половины, затем точку В3 — середину получившегося справа отрезка и т. д. Длины отрезков и т. д. образуют бесконечную геометрическую прогрессию, знаменатель которой равен

Найдем сумму n первых членов этой прогрессии:

При увеличении числа слагаемых n значение дроби 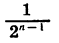приближается к нулю. Действительно,

Поэтому при неограниченном увеличении n разность 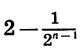становится сколь угодно близкой к числу 2 или, как говорят, стремится к числу 2.

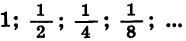
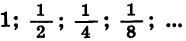
Таким образом, сумма n первых членов геометрической прогрессии при неограниченном увеличении n стремится к числу 2. Число 2 называют суммой бесконечной геометрической прогрессии и пишут:

Это равенство легко истолковать геометрически: сумма длин отрезков 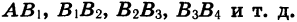равна длине отрезка АВ.

Рассмотрим теперь произвольную геометрическую прогрессию

у которой |q|

Преобразуем выражение в правой части равенства:

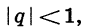
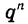
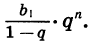
Можно доказать, что если то при неограниченном увеличении n множитель стремится к нулю, а значит, стремится к нулю и произведение Поэтому при неограниченном увеличении n сумма Sn стремится к числу

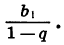
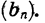
Число называют суммой бесконечной геометрической прогрессии у которой

Это записывают так:

Обозначив сумму прогрессии 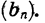буквой S, получим формулу

Заметим, что если 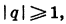то сумма n первых членов геометрической прогрессии при неограниченном увеличении n не стремится ни к какому числу. Бесконечная геометрическая прогрессия имеет сумму только при

Пример:

Найдем сумму бесконечной геометрической прогрессии

У этой прогрессии 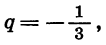значит, условие |q|

Пример:

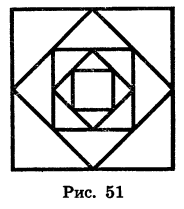
Дан квадрат, сторона которого равна 4 см. Середины его сторон являются вершинами второго квадрата, середины сторон второго квадрата являются вершинами третьего квадрата и т. д. (рис. 51). Найдем сумму площадей всех квадратов.

Из геометрических соображений ясно, что площадь каждого следующего квадрата равна половине площади предыдущего. Таким образом, последовательность площадей квадратов является геометрической прогрессией, первый член которой равен 16, а знаменатель равен 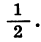Найдем сумму этой геометрической прогрессии:

Значит, сумма площадей всех квадратов равна 32 см2.

Из курса VIII класса нам известно, что каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Чтобы выразить рациональное число — целое число, а n — натуральное, в виде бесконечной десятичной дроби, достаточно разделить числитель на знаменатель. Наоборот, каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число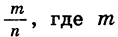. Покажем на примере, как с помощью формулы суммы бесконечной геометрической прогрессии можно представить бесконечную десятичную периодическую дробь в виде отношения

Пример:

Представим бесконечную десятичную периодическую дробь 0,(18) в виде обыкновенной дроби.

По аналогии с конечными десятичными дробями представим бесконечную десятичную дробь 0,(18) в виде суммы:

Слагаемые в правой части равенства — члены геометрической прогрессии, у которой первый член равен 0,18, а знаменатель равен 0,01, т. е. условие 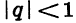выполнено. Найдем сумму этой прогрессии:

Таким же способом можно представить в виде обыкновенной дроби любую бесконечную десятичную периодическую дробь.

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Сумма бесконечной геометрической прогрессии. Алгебра 10 классСкачать

Love Soft

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

Видео:Всё про прогрессии за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Геометрическая прогрессия

q — знаменатель геометрической прогрессии (от лат. qwoti — частное). $$ b_n = b_ cdot q\[10pt] b_n = b_ cdot q^ $$

Если $ b_>0$ и $ q>1$, прогрессия является возрастающей последовательностью, если $ 0 В учебнике Виленкина упоминается «Сумма бесконечно убывающей геометрической прогрессии выражается формулой…» — это неверно, так как при отрицательных q, |q|

Первоначальная формулировка: если $|q|

Cумма геометрической прогрессии со знаменателем q, b=1 :

$$S=1 + q +q^2+cdots=1+q(1+q+cdots) = 1+qcdot S$$

Отсюда выразить S.

Эта же техника может быть использована при вычислении любых самоподобных выражений.

Периодические дроби

Обращение бесконечных периодических дробей в обыкновенные дроби:

$0,(7) = 0,7+0,07+0,007+ldots = 0,7 / (1-0.1) = 7/10 / (9/10) = 7/9$

Геометрическая интерпретация

Сходимость геометрической прогрессии при q=1/2, b=1/2:

Шутка

В магазин заходит бесконечное число математиков. Первый просит килограмм картошки, второй — полкило, третий — четверть… «Понял», — говорит продавец и кладет на прилавок два килограмма.

Видео:БЕСКОНЕЧНО УБЫВАЮЩАЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯСкачать

Легенда о шахматной доске

Шахматы – одна из самых древних игр. Она существует уже многие века, и неудивительно, что с нею связаны различные предания, правдивость которых, за давностью времени, невозможно проверить.

Об одной из подобных легенд и математической составляющей ее содержания мы сегодня и поведём речь. Чтобы понять ее, не нужно вовсе уметь играть в шахматы: достаточно знать, что игра происходит на доске, разграфленной на 64 клетки.

Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.

– Я достаточно богат, чтобы исполнить самое смелое твое пожелание, – сказал царь.– Назови награду, которая тебя удовлетворит, и ты получишь ее.

он удивил царя беспримерной скромностью своей просьбы.

– Повелитель, – сказал Сета,– прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.

– Простое пшеничное зерно? – изумился царь.

– Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью 4, за четвертую – 8, за пятую – 16, за шестую – 32…

–Довольно, – с раздражением прервал его царь.– Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моею милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.

За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.

– Повелитель, – был ответ, – приказание твое исполняется. Придворные математики исчисляют число следуемых зерен.

Царь нахмурился. Он не привык, чтобы повеления его исполнялись так медлительно.

Вечером, отходя ко сну, царь еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.

– Повелитель, – ответили ему,– математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.

– Почему медлят с этим делом? – гневно воскликнул царь. – Завтра, прежде чем я проснусь, все до последнего зерна должно быть выдано Сете. Я дважды не приказываю.

Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.

– Прежде чем скажешь о твоем деле, – объявил Шерам,– я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.

– Ради этого я и осмелился явиться перед тобой в столь ранний час,– ответил старик.– Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…

– Как бы велико оно ни было, – надменно перебил царь, житницы мои не оскудеют. Награда обещана и должна быть выдана…

– Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыни. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду. С изумлением внимал царь словам старца.

– Назови же мне это чудовищное число, – сказал он в раздумье.

– Восемнадцать квинтиллионов четыреста сорок шесть квадриллионов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!

S = 18 446 744 073 709 551 615.

Это количество зерна примерно в 1800 раз превышает мировой урожай пшеницы за год (в 2008 – 2009 аграрном году урожай составил 686 млн тонн), то есть превышает весь урожай пшеницы, собранный за всю историю человечества.

Индусский царь не в состоянии был выдать подобной награды. Но он легко мог бы, будь он силен в математике, освободиться от столь обременительного долга. Для этого нужно было лишь предложить Сете самому отсчитать себе зерно за зерном всю причитавшуюся ему пшеницу.

В самом деле: если бы Сета, принявшись за счет, вел его непрерывно день и ночь, отсчитывая по зерну в секунду, он в первые сутки отсчитал бы всего 86 400 зерен. Чтобы отсчитать миллион зерен, понадобилось бы не менее 10 суток неустанного счета. Один кубический метр пшеницы он отсчитал бы примерно за полгода. И осталось бы отсчитать ещё 1 499 999 999 999 м3. Вы видите, что, посвятив счету даже весь остаток своей жизни, Сета получил бы лишь ничтожную часть потребованной им награды.

Экспоненциальный рост

Стремительное возрастание значений величины, подобное тому, которое мы наблюдали, в математике называется экспоненциальным ростом.

Экспоненциальный рост – возрастание величины, когда скорость роста пропорциональна значению самой величины. Говорят, что такой рост подчиняется экспоненциальному закону. В случае дискретной области определения с равными интервалами его еще называют геометрическим ростом (значения функции образуют геометрическую прогрессию).

Для любой экспоненциально растущей величины чем большее значение она принимает, тем быстрее растет. Также это означает, что величина зависимой переменной и скорость ее роста прямо пропорциональны.

Примером экспоненциального роста может быть рост числа бактерий в колонии до наступления ограничения ресурсов.

Экспоненциальный рост противопоставляется более медленным (на достаточно длинном промежутке времени) линейной или степенной зависимостям.

Сумма бесконечной геометрической прогрессии

Геометрическая прогрессия бывает убывающей, если знаменатель по модулю меньше единицы.

число $q^n$ при достаточно больших n может стать сколь угодно малым. И с ростом n сумма n членов геометрической прогрессии $S_n = b_1 (1 – q^n) / (1 – q)$ становится ближе к числу $S = b_1 / (1 – q)$. (Так рассуждал, например, Ф. Виет). Число S называется суммой бесконечно убывающей геометрической прогрессии. Тем не менее, долгие века вопрос о том, какой смысл имеет суммирование ВСЕЙ геометрической прогрессии, с ее бесконечным числом членов, не был достаточно ясен математикам.

Убывающую геометрическую прогрессию можно видеть, например, в апориях Зенона «Деление пополам» и «Ахиллес и черепаха». В первом случае наглядно показывается, что вся дорога (предположим, длины 1) является суммой бесконечного числа отрезков 1/2, 1/4, 1/8 и т. д. Так оно, конечно, и есть с точки зрения представлений о конечной сумме бесконечной геометрической прогрессии. И все же – как такое может быть?

Прогрессия с коэффициентом 1/2

В апории про Ахиллеса ситуация чуть более сложная, т. к. здесь знаменатель прогрессии равен не 1/2, а какому-то другому числу. Пусть, например, Ахиллес бежит со скоростью v, черепаха движется со скоростью u, а первоначальное расстояние между ними равно l. Это расстояние Ахиллес пробежит за время l/v, черепаха за это время сдвинется на расстояние lu/v. Когда Ахиллес пробежит и этот отрезок, дистанция между ним и черепахой станет равной $l (u/v)^2$, и т. д. Получается, что догнать черепаху – значит найти сумму бесконечно убывающей геометрической прогрессии с первым членом l и знаменателем u/v. Эта сумма – отрезок, который в итоге пробежит Ахиллес до места встречи с черепахой – равен $l / (1 – u/v) = lv / (v – u)$. Но, опять-таки, как надо интерпретировать этот результат и почему он вообще имеет какой-то смысл, долгое время было не очень ясно.

От апорий Зенона один шаг до понятий предела, предельного перехода, производной и интеграла — но на этот шаг человечеству понадобилось 2000 лет. Через 300 лет после того, как это шаг сделан и подробно изложен в учебниках для средней школы, […] смотрят на апории как баран на новые ворота.

Видео:Нахождение суммы бесконечно убывающей геометрической прогрессииСкачать

Предел складывания бумаги

Предел складывания бумаги пополам — физический феномен, суть которого состоит в том, что лист обычной бумаги размера А4 можно сложить пополам не более 7 раз. Он происходит из-за быстроты роста показательной функции.

Если бумагу сложили пополам пять раз, то количество слоёв будет два в степени пять, то есть тридцать два.

Если бумагу сложили пополам 7 раз, то количество слоёв будет два в степени 7, то есть 128.

Уже в Древнем Египте знали не только арифметическую, но и геометрическую прогрессию. Вот, например, задача из папируса Райнда: «У семи лиц по семи кошек; каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа этого ряда и их сумма?»

Людей всего 7, кошек 72 = 49, они съедают всего 73 = 343 мыши, которые съедают всего 74 = 2401 колосьев, из них вырастает 75 = 16807 мер ячменя, в сумме эти числа дают 19 607.

Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.

Видео:Бесконечно убывающая геометрическая прогрессия. Практическая часть. 9 класс.Скачать

Задача

Найти сумму первых 20 членов: $$2+22+222+2222+ldots$$

💡 Видео

10 класс. Алгебра. Решение уравнений. Бесконечно убывающая геометрическая прогрессияСкачать

Сумма первых n членов геометрической прогрессии. 9 класс.Скачать

Бесконечно убывающая геометрическая прогрессия. Сумма бесконечно убывающей геометрической прогрессииСкачать

Сумма бесконечно убывающей геометрической прогрессииСкачать

Бесконечно убывающая геометрическая прогрессия. Подготовка к экзаменам. 97 часть. 9 класс.Скачать

Сумма бесконечной геометрической прогрессии (q меньше 1). 9 классСкачать

Бесконечно убывающая геометрическая прогрессия | Алимов 10 классСкачать

Математика для всех. Алексей Савватеев. Лекция 3.4. Убывающая геометрическая прогрессияСкачать

Бесконечно убывающая геометрическая прогрессия. Видеоурок 2. Алгебра 10 классСкачать

Научно-технический рэп - Сумма бесконечно убывающей геометрической прогрессииСкачать