Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
Решение сравнений по модулю
Этот калькулятор находит решения линейных сравнений, или сравнений первой степени по модулю m
Решение сравнений по модулю
Решений нет
Сравнение по модулю
Сравнение двух целых чисел по модулю натурального числа m — математическая операция, позволяющая ответить на вопрос о том, дают ли два выбранных целых числа при делении на m один и тот же остаток. Арифметические операции с остатками чисел по одному и тому же модулю образуют модулярную арифметику.
Сравнимость чисел a и b по модулю сравнения m записывается как
называется сравнением первой степени или линейным сравнением по модулю m.
Для проверки существования решений сравнения сначала вычисляется НОД(a, m). Если b не кратно полученному НОД, то у сравнения нет решений.
Если кратно, то количество решений по модулю m равно полученному НОД.
Существует несколько алгоритмов нахождения всех решений сравнения, но в данном калькуляторе применяется алгоритм решения линейных диофантовых уравнений с двумя переменными. В самом деле, сравнение эквивалентно следующему линейному диофантовому уравнению:
поэтому я использовал уже реализованный калькулятор решения линейных диофантовых уравнений для получения общей формулы решения, после чего выбрал все частные решения в диапазоне от 0 до m.
Видео:✓ Сравнение по модулю. Арифметика остатков | Ботай со мной #034 | Борис ТрушинСкачать
Онлайн НОД и НОК, разложение на множители, сравнения по модулю
С помощью данного онлайн-калькулятора можно вычислить НОД и НОК нескольких чисел, разложить число на простые множители, решить линейные и нелинейные сравнения, системы сравнений.
Наибольший общий делитель (НОД, англ. GCD) нескольких целых чисел есть наибольшее из натуральных чисел, которое делит каждое из данных чисел.
Наименьшее общее кратное (НОК, англ. LCM) нескольких целых чисел есть наименьшее из натуральных чисел, которое делится на каждое из данных чисел.
Запишите свои числа через запятую и/или пробел и нажмите кнопку.
Видео:Теория чисел. 6. Методы решения сравнений 1 й степениСкачать
Сравнение чисел по модулю
Определение 1. Если два числа 1 ) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.
Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде
| a=sp+r, | (1) |
где s — число, и r одно из чисел 0,1, . p−1.
1 ) В данной статье под словом число будем понимать целое число.
Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа
  |
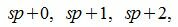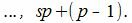Но эти числа можно получить задав r равным 0, 1, 2. p−1. Следовательно sp+r=a получит всевозможные целые значения.
Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s1p+r1. Тогда
 |
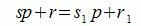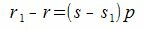 | (2) |
Так как r1 принимает один из чисел 0,1, . p−1, то абсолютное значение r1−r меньше p. Но из (2) следует, что r1−r кратно p. Следовательно r1=r и s1=s.
Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).
Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.
Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда
 |
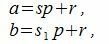где s и s1 некоторые целые числа.
Разность этих чисел
 | (3) |
делится на p, т.к. правая часть уравнения (3) делится на p.
Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.
Доказательство. Обозначим через r и r1 остатки от деления a и b на p. Тогда
 |
 |
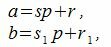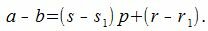По утверждению a−b делится на p. Следовательно r−r1 тоже делится на p. Но т.к. r и r1 числа 0,1. p−1, то абсолютное значение |r−r1| Свойство 1. Для любого a и p всегда
| a≡a mod (p). |
Свойство 2. Если два числа a и c сравнимы с числом b по модулю p , то a и c сравнимы между собой по тому же модулю, т.е. если
| a≡b mod (p), b≡c mod (p). |
| a≡c mod (p). |
Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.
| a≡b mod (p) и m≡n mod (p), |
| a+m≡b+n mod (p) и a−m≡b−n mod (p). |
Действительно. Так как a−b и m−n делятся на p, то
| (a−b)+ (m−n)=(a+m)−(b+n) , |
| (a−b)−(m−n)=(a−m)−(b−n) |
также делятся на p.
Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.
| a≡b mod (p) и m≡n mod (p), |
| am≡bn mod (p). |
Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно
| am≡bm mod (p). |
Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит
| bm≡bn mod (p). |
Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).
| a≡b mod (p). |
| a k ≡b k mod (p). |
где k некоторое неотрицательное целое число.
Действительно. Имеем a≡b mod (p). Из свойства 4 следует
| a·a≡b·b mod (p). |
| a·a·a≡b·b·b mod (p). |
| . |
| a k ≡b k mod (p). |
Все свойства 1-5 представить в следующем утверждении:
Утверждение 4. Пусть f(x1, x2, x3, . ) целая рациональная функция с целыми коэффициентами и пусть
| a1≡b1, a2≡b2, a3≡b3, . mod (p). |
| f(a1, a2, a3, . )≡f(b1, b2, b3, . ) mod (p). |
При делении все обстоит иначе. Из сравнения
| am≡bm mod (p) |
не всегда следует сравнение
| a≡b mod (p). |
Утверждение 5. Пусть
| am≡bm mod (p), |
| a≡b mod (p/λ), |
Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда
| m=m1λ и k=k1λ. |
Так как m(a−b) делится на k, то
 |
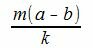имеет нулевой остаток. Тогда
  . |
 |
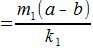имеет нулевой остаток, т.е. m1(a−b) делится на k1. Но числа m1 и k1 числа взаимно простые. Следовательно a−b делится на k1=k/λ и, тогда, a≡b mod (p/λ).
Утверждение 6. Если
| a≡b mod (p) |
и m является один из делителей числа p, то
| a≡b mod (m). |
Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.
Утверждение 7. Если
| a≡b mod (p), a≡b mod (q), a≡b mod (s) |
| a≡b mod (h), |
где h наименьшее общее кратное чисел p,q,s.
Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.
В частном случае, если модули p,q,s взаимно простые числа, то
| a≡b mod (h), |
Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.
📺 Видео
Сравнение по модулю (Теория и примеры)Скачать
Сравнения по модулю: решение задач №1 | Vasily mathsСкачать
Т.чисел 10. Система сравнений. Два метода решенияСкачать
Т.чисел 8. Система сравнений. Китайская теорема об остаткахСкачать
Модуль числа. Практическая часть. 6 класс.Скачать
Уравнения с модулемСкачать
Уравнения с модулем. Часть 2 | Математика | TutorOnlineСкачать
Теория чисел. 4. Сравнения. Свойства сравненийСкачать
Модуль числа. 6 класс.Скачать
Т.чисел 9. Система сравнений Метод подстановкиСкачать
Разбор заданий по теме «Сравнение по модулю».Скачать
Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать
Решение сравнений первой степениСкачать
Решение уравнения с модулем |x+8|+|x-3|+|x+2|=1.Скачать
Контрольная работа. Уравнения с МОДУЛЕМСкачать
Теория чисел. 7. Решаем сравнения 1 й степениСкачать
Как решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать
