Решение уравнений систем графиков в mathcad (7 видео)

Решение систем уравнений в MathCad

Для решения уравнений в Mathcad можно воспользоваться двумя способами. Эти способы были частично рассмотрены в разделе «Решение уравнений»:

Содержание

Использование метода Given — Find:
Использование метода Solve:
Графический способ решения систем алгебраических уравнений с использованием программного пакета MathCAD
Тема 7. Решение дифференциальных уравнений и систем в MathCad
🔍 Видео

Видео:Основы работы в Mathcad ГрафикиСкачать

Использование метода Given — Find:

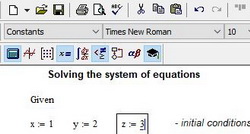
В рабочем поле mathcad записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения системы уравнений численными методами.

Затем указывается начальное приближение для искомых переменных. Это нужно для увеличения скорости и точности решения системы. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю для всех переменных, при этом, если окажется, что система имеет несколько решений, то есть риск не определить все корни. Поэтому лучше всегда задавать приближение

Рис. 1. Ввод исходных данных в поле mathcad

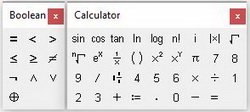
Далее вводятся уравнения. Их можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)

Рис. 2. Панели Boolean и Calculator

Когда уравнения записаны вводится функция Find(x, y, z. ) (где х, y, z. — переменные). Это функция, которая возвращает результат решения системы. Значение функции Find() можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах (см. рис. 3). При решении систем уравнений в mathcad результатом всегда будет являтся матрица значений

Рис. 3. Ввод функции Find()

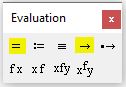
Для того чтобы увидеть результат решения системы уравнений, после Find(x, y, z. ) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 4).

Рис. 4. Панель «Evaluation»

В зависимости от сложности системы через определенное время MathCad выведет результат. На рис. 5 можно рассмотреть синтаксис и результат решения системы уравнений. Обратите внимание, что можно присваивать результат решения системы матричной переменной и можно работать с отдельными ее элементами

Рис. 5. Результат численного решения системы уравнений

Mathcad позволяет решать системы уравний в символьном виде. Обычно это полезно, когда требуется получить не точное значение переменных, а их выражения через константы. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, y и z, то результат выведется в символьном виде (см. рис. 6). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата. Как правило, символьное решение получается громоздким, поэтому не всегда рекомендуется использовать этот метод

Рис. 6. Результат символьного решения системы уравнений

Видео:MathCAD Решение системы уравненийСкачать

Использование метода Solve:

Как показывает практика, методом solve иногда удается решить системы уравнений, которые не поддаются решению с помощью функции Find()

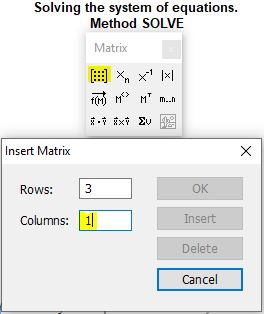
Синтаксис следующий: на панели matrix нажимаем иконку Matrix or Vector и в появившемся окне указываем количество уравнений входящих в систему. В нашем примере их будет три (см. рис. 7)

Рис. 7. Создание матрицы для метода SOLVE

Заполняем систему, вводя последовательно все уравнения используя логический символ «ровно» из панели Boolean. Каждый элемент матрицы-столбца содержит одно уравнение (см. рис. 8)

Рис. 8. Ввод системы уравнений для метода SOLVE

Когда все уравнения введены, убедитесь, что курсор ввода находится в вашей матрице и затем нажмите кнопку «solve» из панели Symbolic. Появится служебное слово (функция) solve. Далее поставте запятую и введите последовательно все переменные, относительно которых необходимо решить систему уравнений (см. рис. 9)

Рис. 9. Синтаксис метода SOLVE для решения систем

Уведите курсор в свободное поле mathcad и дождитесь окончания решения системы. Обратите внимание, что мы не вводили начальные приближения. Даный метод их назначает автоматически. Обратите так же внимание, что для решения системы в символьном виде синтаксис аналогичен (см. рис. 10)

Рис. 10. Синтаксис метода SOLVE для решения систем

Как показывает моя инженерная практика, решение систем в символьном виде сопряжено с большими вычислительными трудностями. То есть иногда решение системы занимает массу времени, и в итоге mathcad выдает выражение для одной переменной непомерной длины, которое нельзя использовать. Поэтому рекомендуется прменять эту возможность лишь в крайних случаях и по возможности «помогать» mathcad, заменяя константы известными числовыми значениями

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Видео:Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

Графический способ решения систем алгебраических уравнений с использованием программного пакета MathCAD

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Графический способ решения систем алгебраических уравнений

с использованием программного пакета Mat h CAD

Автор работы : Сенашева Юлия Викторовна, ученица 7 класса

Научный руководитель : Несивкина Галина Анатольевна

учитель математики первой квалификационной категории.

Учреждение : МБОУ «Ширинская» средняя общеобразовательная школа №18

Ширинского района Республики Хакасия.

1.1.Алгоритм построения графика линейного уравнения с помощью MathCAD;……4

1.2. Исследование расположения прямой, в зависимости от изменения значения k,

в программе MathCAD . 5.

1.3 Алгоритм графического метода решения систем линейных уравнений

с помощью программы MathCAD………………………………………………………6

Актуальность работы : При изучении следующих разделов математики: взаимное расположение графиков линейных функций , графический способ решения системы линейных уравнений столкнулась с тем, что для глубокого исследования этих тем ,отводиться мало времени. Считаю, что изучение этого материала требует более детального рассмотрения, так как он прослеживается в различных заданиях повышенной сложности, в задачах математических олимпиад , в заданиях на ОГЭ, на ЕГЭ и вступительных экзаменов в Высшие Учебные Заведения.

Мотивация : как увеличить время на изучение тем: взаимное расположение графиков линейных функций, графический способ решения системы линейных уравнений.

Проблема: необходимо найти удобный , наглядный, а самое главное быстрый способ построения графиков уравнений.

Гипотеза : объект исследования «Линейная функция» ( А.Г.Мордкович ,Алгебра 7 класс,глава2),»Системы двух линейных уравнений с двумя переменными» (глава3).

Цель работы : показать графический способ решение систем алгебраических уравнений с применением популярного инженерного программного пакета MathCAD. Исследование предоставляет базовые знания работы с программой MathCAD, как они могут быть применены для решения системы двух линейных уравнений с двумя переменными графическим методом.

Результаты исследования : в процессе исследования:

-из множества программ, позволяющих рисовать графики функций, выполнять построения, была выбрана MathCAD , которая является средой визуального программирования, то есть не требует знания специфического набора команд. Простота освоения пакета, дружественный интерфейс, относительная непритязательность к возможностям компьютера явились главными причинами того, что именно этот пакет был выбран мной для решения данной проблемы;

-изучила алгоритм построения графика линейного уравнения с помощью программы MathCAD;

-изучила графический метод решения систем линейных уравнений с помощью программы MathCAD и убедилась в том, что графический метод решения системы линейных уравнений имеет большое значение.

С помощью программы MathCAD мною были выполнены все задания из задачника Алгебра 7 класс по этой теме, ряд заданий олимпиадного характера и задания для подготовки к ОГЭ. Я смогла за короткий срок выполнить большой объем учебного материала, причем в очень наглядной и доступной форме.В процессе работы не тратила время на составление таблиц и построение графиков в тетради .Получился большой запас времени на отработку заданий повышенной сложности.

Перспективы: использовать программный продукт MathCAD., для дальнейшего изучения алгебры 7 класса (глава 8,параграф38.) ,решения задач повышенной сложности, решения заданий из ОГЭ.

В данной работе были рассмотрены примеры , каким образом решаются на MathCAD разнообразные математические задачи (решение систем линейных уравнений). Данная работа поможет ученикам быстро освоить основные навыки работы с пакетом MathCAD, а примеры и способы решения помогут их закрепить для решения новых задач.

1.1 Алгоритм построения графика линейного уравнения с помощью программы MathCAD;

№ 7.17. На координатной плоскости хОу постройте график уравнения:

1.Задать функцию, приведенную выше. Вставить оператор абсолютного значения

2.На вкладке Графики в группе Кривые щелкнуть Вставить график , а затем выбрать График ХУ .

Появиться пустой пустой график

3.В местозаполнителе оси У ,в левой или правой части ввести функцию у = -х+4.

4.В местозаполнителе оси Х внизу графика ввести х. Нажать клавишу «Ввод», появиться линейная кривая.

№ 8.28. Постройте график линейной функции у = х+4 и у=2х

а) координаты точек пресечения графика с осями координат;

б) значение у, соответствующее значению х=—2;-1;1.

в ) значение х ,которому соответствует значение у, равное-2;2;4.

1.Задать функцию, приведенную выше. Вставить оператор абсолютного значения

2.На вкладке Графики в группе Кривые щелкнуть Вставить график , а затем выбрать График ХУ

Появиться пустой график.

3.В местозаполнителе оси У ,в левой или правой части ввести функцию у = х+4.

4.В местозаполнителе оси Х внизу графика ввести х. Нажать клавишу «Ввод», появиться линейная

5.Установить курсор справа от функции. Щелкнуть Добавить кривую .

Появиться новый местозапонитель оси У под текущим местозаполнителем

А ) Найти координаты точек пресечения графика с осями координат.

На графике точки пересечения: х=0,у=- 4

Б) Найти значение у, соответствующее значению х = —2;-1;1.

В) Найти значение х ,которому соответствует значение у, равное-2;2;4.

Внесем данные и получим следующее распределение по столбцам .

1.2. Исследование расположения прямой, в зависимости от изменения значения k, в программе MathCAD;

у=3х+4, у=3х, у = -3х,у=2х, у=3х-4,

1.3.Алгоритм графического метода решения систем линейных уравнений с помощью программы MathCAD;

№ 11.10 .Решить графически систему уравнений (задачник Алгебра7 класс, часть 2)

Ответ: система имеет одно решение (2;2)

Пример1.Решить систему уравнений

Ответ: система не имеет решений

Решить систему уравнений

Ответ: система имеет бесконечно много решений.

Вывод : графический метод решения системы линейных уравнений имеет большое значение. С его помощью можно сделать следующие важные выводы:

— графиком обоих уравнений системы линейных уравнений являются прямые;

-эти прямые могут пересекаться, причем только в одной точке,- это значит, что система имеет единственное решение;

-эти прямые могут быть параллельны — это значит, что система не имеет решений( система несовместна);

-эти прямые могут совпасть — это значит, что система имеет бесконечно много решений (система не определена).

Видео:8. MathCad. Решение систем линейных алгебраических уравненийСкачать

Тема 7. Решение дифференциальных уравнений и систем в MathCad

Краткие теоретические сведения

Для решения дифференциальных уравнений с начальными условиями система Mathcad имеет ряд встроенных функций:

rkfixed – функция для решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;

Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;

Odesolve – функция, решающая ОДУ блочным методом.

Ниже приведено описание стандартной функции rkfixed с указанием параметров функции.

y – вектор начальных условий из k элементов ( k – количество уравнений в системе);

x1 и x2 – левая и правая границы интервала, на котором ищется решение ОДУ или системы ОДУ;

p – число точек внутри интервала (x1, x2), в которых ищется решение;

D – вектор, состоящий из k-элементов, который содержит первую производную искомой функции или первые производные искомых функций, если речь идет о решении системы.

Результатом работы функции является матрица из p +1 строк, первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – сами решения.

На рисунке 2.7.1 приведены конкретные примеры решения различных дифференциальных уравнений и систем ОДУ в MathCAD .

Рисунок 2.7.1 – Примеры решения дифференциальных уравнений и систем

При решении дифференциального уравнения первого порядка нужно создать вектор начальных условий из одного элемента Y 1 , который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции rkfixed указывается имя вектора Y , границы интервала, на котором ищется решение уравнения, например, (0 ; 2), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D . В результате получается матрица z , в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой результирующей функции. При построении графика функции первый столбец полученной матрицы указывается как аргумент, второй столбец – как функция.

При решении системы дифференциальных уравнений нужно создать вектор начальных условий из двух элементов, например, вектор v , который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции rkfixed указывается имя вектора v , и границы интервала, на котором ищется решение уравнения, например, (0 ; 5), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D . В результате получается матрица s , в первом столбце которой содержатся значения аргумента искомых функций, во втором и третьем столбцах – значения самих функций при соответствующем значении аргумента. При построении графика можно воспользоваться первым столбцом полученной матрицы как аргументом, а вторым и третьим столбцами – как функциями.

На рисунке 2.7.2 приведен пример решения дифференциального уравнения второго порядка с использованием функции rkfixed . Необходимо решить дифференциальное уравнение второго порядка с заданными начальными условиями вида:

Рисунок 2.7.2 – Пример решения дифференциальных уравнений второго порядка с помощью rkfixed

Для решения уравнения с помощью функции rkfixed нужно выполнить замену переменных и привести дифференциальное уравнение второго порядка к двум дифференциальным уравнениям первого порядка. Вид этих уравнений приведен ниже.

Документ формируется точно так же, как и при решении системы ОДУ.

На рисунке 2.7.2 показана возможность вычисления вектора второй производной найденной функции – вектора а, построены графики исходной функции, функций первой и второй производных.

Практическая часть темы 7

7.1 Решение дифференциальных уравнений первого порядка

Последовательность действий для р ешения дифференциального уравнения первого порядка такова:

q сформировать вектор начальных условий из одного элемента, присвоив начальное значение искомой функции переменной с индексом, например: или (в зависимости от значения переменной ORIGIN );

q определить вектор-функцию из одного элемента, которая содержит первую производную неизвестной функции:

· набрать имя функции с двумя параметрами: первый параметр – аргумент искомой функции (независимая переменная), второй – имя вектора, содержащего искомую функцию (можно использовать имя вектора начальных условий), например, D ( x , Y );

· набрать оператор «:=» и выражение для первой производной (выразить из дифференциального уравнения), в котором вместо имени искомой функции подставлен первый элемент вектора-параметра, например, для уравнения вектор-функция будет определятся следующим образом: ( если ORIGIN = 0 , подставлять );

q присвоить некоторой переменной значение функции rkfixed , указав в скобках следующие параметры:

· первый – имя вектора начальных условий,

· второй – левая граница интервала, на котором ищется решение, в виде числовой константы,

· третий – правая граница интервала, на котором ищется решение, в виде числовой константы,

· четвертый – количество точек, в которых ищется решение,

· пятый – имя вектора-функции, описывающего первую производную, без параметров;

например: ,

(в результате получится матрица Z , в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой функции);

q вывести матрицу, содержащую решение ДУ с помощь оператора «=», например: Z = ;

q построить график найденной функции ( см. тему 5 ), указав в качестве аргумента по оси абсцисс столбец , а в качестве значения функции по оси ординат – столбец ( если ORIGIN = 0 , набирать соответственно и ).

Пример 7.1 Найти численное решение дифференциального уравнения первого порядка на интервале от 0.2 до 5 в 1000 точках, при начальном условии y (0)=0.1.

Выполнить графическую интерпретацию результатов.

7.2 Решение систем дифференциальных уравнений

Последовательность действий для р ешения системы дифференциальных уравнений первого порядка такова (описана для значения ORIGIN =0 ):

q перейти в исходной системе уравнений к однотипным обозначениям функций и выразить первые производные,

например, систему можно преобразовать в ;

q в документе MathCad сформировать вектор начальных условий, количество элементов которого равно количеству уравнений системы, присвоив его некоторой переменной (см. тему 2);

например, ;

q определить вектор-функцию, которая содержит первые производные искомых функций:

· набрать имя функции с двумя параметрами: первый параметр – аргумент искомых функций (независимая переменная), второй – имя вектора, содержащего искомые функции (можно использовать имя вектора начальных условий), например, D ( t , V );

(Замечание: если независимая переменная явно не присутствует в системе, то в качестве ее имени можно выбрать любую переменную)

· набрать оператор «:=» и вставить шаблон вектора, количество элементов которого равно количеству уравнений системы (см. тему 2)

· набрать в качестве элементов вектора правые части системы уравнений, в которых искомые функции представлены соответствующими элементами вектора-параметра, например,

;

q присвоить некоторой переменной значение функции rkfixed , указав в скобках следующие параметры:

· первый – имя вектора начальных условий,

· второй – левая граница интервала, на котором ищется решение, в виде числовой константы,

· третий – правая граница интервала, на котором ищется решение, в виде числовой константы,

· четвертый – количество точек, в которых ищется решение,

· пятый – имя вектора-функции, описывающего первые производные, без параметров;

например: ,

(в результате получится матрица Z , в первом столбце которой содержатся значения аргумента искомых функций, во втором – значения первой функции, в третьем – значения второй функции и т. д.);

q вывести матрицу, содержащую решение системы ДУ с помощь оператора «=», например: Z = ;

q построить графики найденных функций ( см. тему 5 ), указав в качестве аргумента по оси абсцисс первый столбец матрицы решений, например, , а в качестве значений функций по оси ординат – остальные столбцы матрицы через запятую, например, , и т. д.