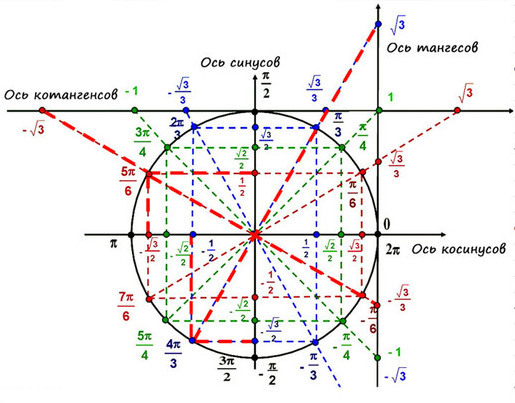
Чтобы уверенно решать простейшие уравнения с тангенсом или котангенсом нужно знать значения стандартных точек на круге и стандартные значения на осях тангенсов и котангенсов (если в этом материале есть пробелы, читайте « Как запомнить тригонометрический круг »).
Видео:Тригонометрическая окружность. Как выучить?Скачать
Алгоритм решения простейших уравнений с тангенсом
Давайте с вами рассмотрим типичное уравнение, например, (tgx=sqrt).
Пример. Решить уравнение (tgx=sqrt).
Чего от нас здесь хотят? Чтобы мы написали все такие значения угла в Пи, для которых тангенс равен корню из трех. Причем написать надо именно все такие углы. Давайте нарисуем тригонометрический круг и ось тангенсов…
…и обозначим то место на оси, куда мы должны попасть в итоге.
Теперь найдем через какие точки на окружности мы должны идти, чтобы попасть в этот самый корень из трех –проведем прямую через начало координат и найденную точку на оси тангенсов.
Точки найдены. Давайте подпишем значение одной из них…
…и запишем окончательный ответ – все возможные варианты значений в Пи, находящиеся в отмеченных точках: (x=frac+πn), (n∈Z).
Замечание. Вы, наверно, обратили внимание, что в отличие от уравнений с синусом и косинусом , здесь записывается только одна серия корней, причем в формуле добавляется (πn), а не (2πn). Дело в том, что в любом уравнении с тангенсом решением получаются две точки на окружности, которые находятся друг от друга на расстоянии (π). Благодаря этому значение обеих точек можно записать одной формулой в виде (x=t_0+πn), (n∈Z).
Пример. Решить уравнение (tgx=-1).
Итак, окончательный алгоритм решения подобных задач выглядит следующим образом:
Шаг 1. Построить окружность, оси синусов и косинусов, а также ось тангенсов.
Шаг 2. Отметить на оси тангенсов значение, которому тангенс должен быть равен.
Шаг 3. Соединить прямой линией центр окружности и отмеченную точку на оси тангенсов.
Шаг 4. Найти значение одной из точек на круге.
Шаг 5. Записать ответ используя формулу (x=t_0+πn), (n∈Z) (подробнее о формуле в видео), где (t_0) – как раз то значение, которые вы нашли в шаге 4.
Специально для вас мы сделали удобную табличку со всеми шагами алгоритма и разными примерами к нему. Пользуйтесь на здоровье! Можете даже распечатать и повесить на стенку, чтоб больше никогда не ошибаться в этих уравнениях.
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Алгоритм решения простейших уравнений с котангенсом
Сразу скажу, что алгоритм решения уравнений с котангенсом почти такой же, как и с тангенсом.
Шаг 1. Вопрос у нас практически тот же – из каких точек круга можно попасть в (frac<sqrt>) на оси котангенсов?
Строим круг, проводим нужные оси.
Теперь отмечаем на оси котангенсов значение, которому котангенс должен быть равен…
…и соединяем центр окружности и точку на оси котангенсов прямой линией.
По сути точки найдены. Осталось записать их все. Вновь определяем значение в одной из них…
…и записываем окончательный ответ по формуле (x=t_0+πn), (n∈Z), потому что у котангенса период такой же как у тангенса: (πn).
Кстати, вы обратили внимание, что ответы в задачах совпали? Здесь нет ошибки, ведь для любой точки круга, тангенс которой равен (sqrt), котангенс будет (frac<sqrt>).
Разберем еще пример, а потом подведем итог.
Пример. Решить уравнение (ctgx=-1). Здесь подробно расписывать не буду, так как логика полностью аналогична вышеизложенной.
Итак, алгоритм решения простейших тригонометрических уравнений с котангенсом:
Шаг 1. Построить окружность и оси синусов и косинусов, а также ось котангенсов.
Шаг 2. Отметить на оси котангенсов значение, которому котангенс должен быть равен.
Шаг 3. Соединить центр окружности и точку на оси котангенсов прямой линией.
Шаг 4. Найти значение одной из точек на круге.
Шаг 5. Записать ответ используя формулу (x=t_0+πn), (n∈Z), где (t_0) – как раз то значение, которые вы нашли в шаге 4. И табличка в награду всем дочитавшим до этого места.
Примечание. Возможно, вы обратили внимание, что при решении примеров 2 и 3 в обеих табличках мы использовали функции (arctg) и (arcctg). Если вы не знаете, что это – читайте эту статью.
Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать
Тригонометрические уравнения
Решение простейших тригонометрических уравнений
Градусы и радианы
Знакомство с тригонометрической окружностью
Повороты на тригонометрической окружности
Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».
Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .
1 радиан = 180/π ≈ 57,3 градусов
Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.
Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!
О графиках синуса, косинуса и тангеса поговорим в другой статье.
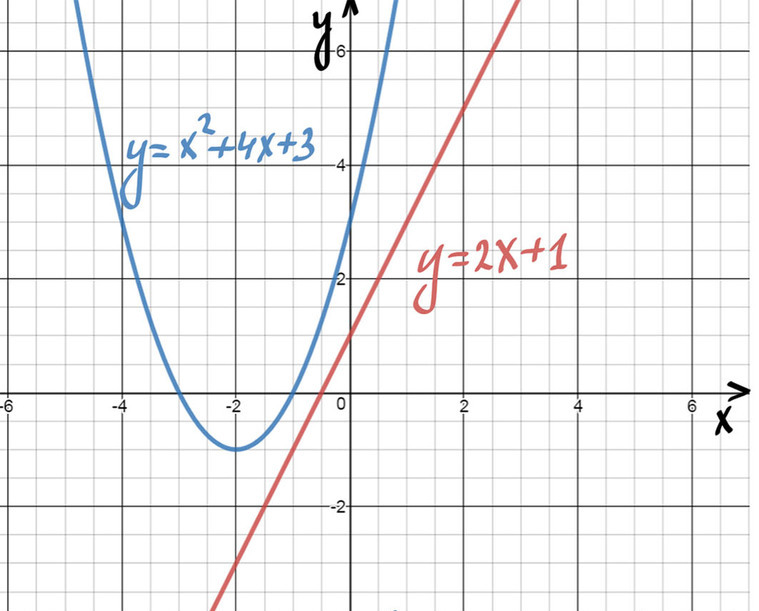
А сейчас начем с декартовой (прямоугольной) системы координат.
Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.
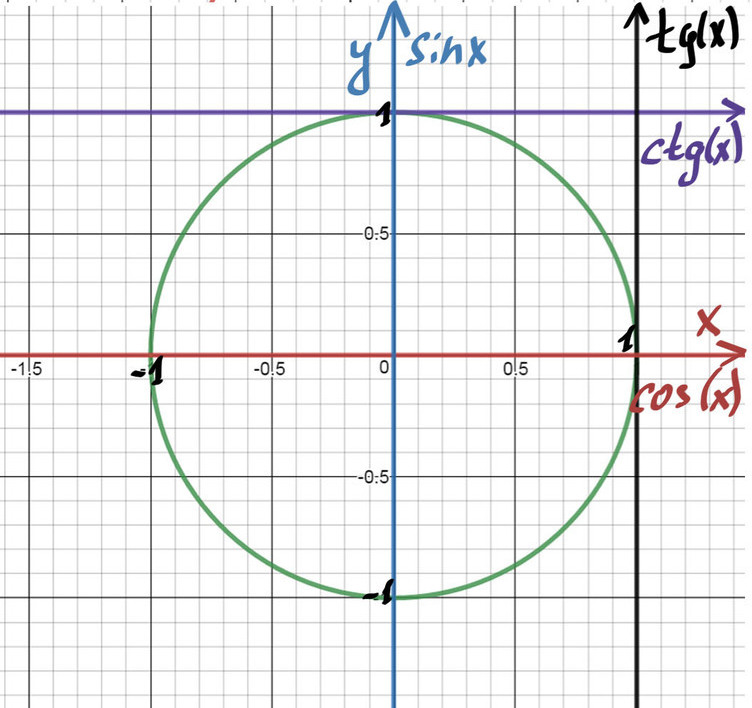
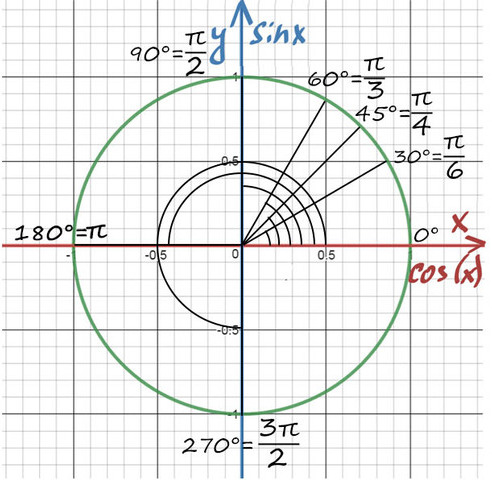
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:
Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.
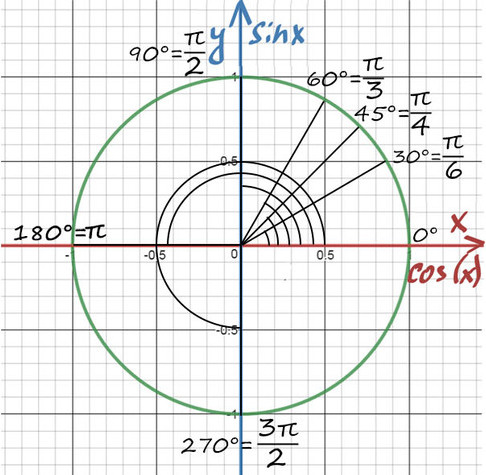
А теперь отметим основные значения градусов и радиан на окружности.
Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.
Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).
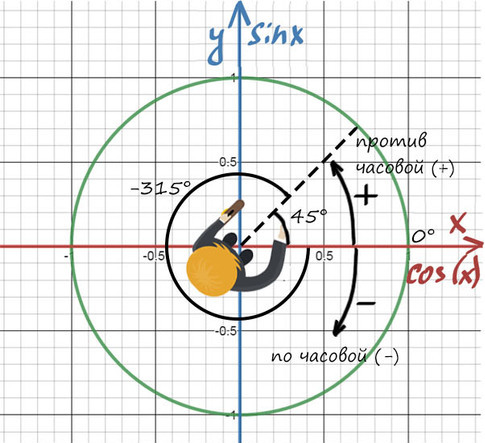
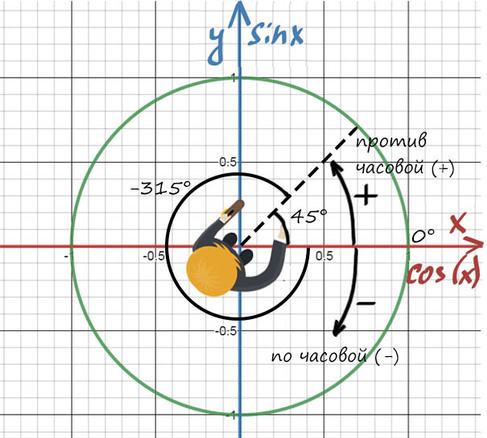
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):
От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).
Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).
Главное — направление, куда мы будем смотреть, а не угол!
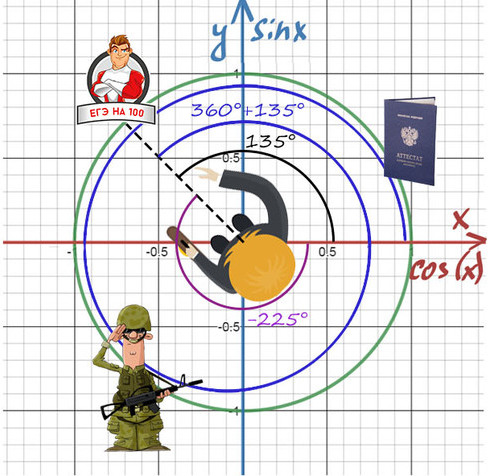
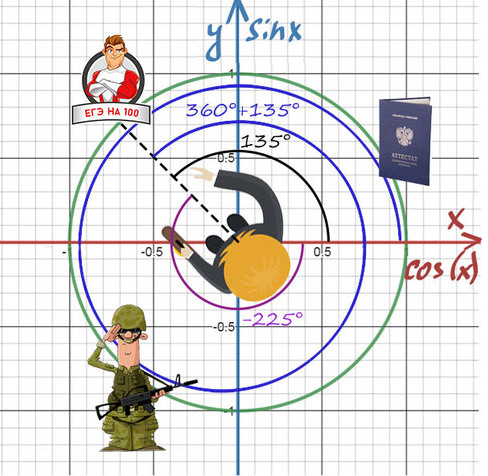
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!
Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.
А теперь у тебя есть два пути:
Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:
А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.
Сразу попробуем разобрать на примере:
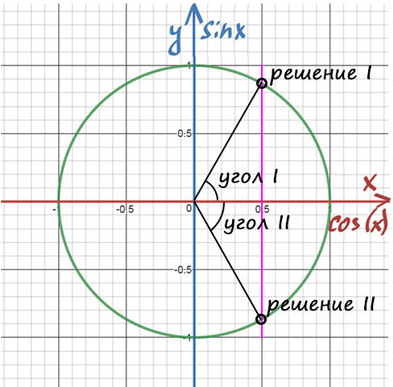
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.
2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.
Дело за малым — найти эти углы.
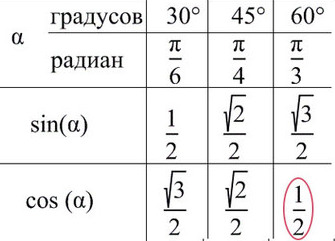
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.
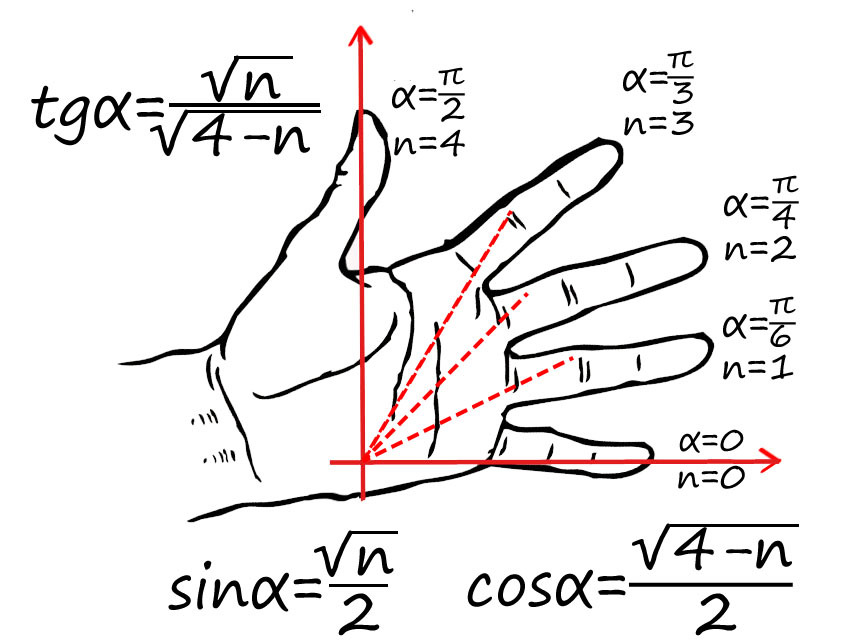
Или запомнить такой прием:
Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).
Например, требуется найти sin(π/2) : π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.
cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.
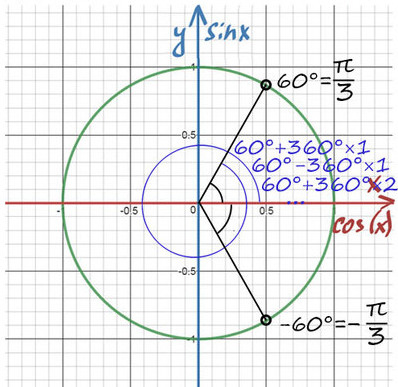
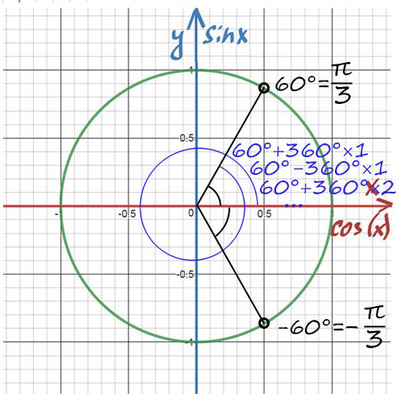
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).
Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).
И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:
Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на . =-225°=135°=495°=.
То же самое и здесь! Разные углы могут отражать одно и то же направление.
Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.
Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.
И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)
Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.
Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.
Ответ: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.
Пример №2. 2sinx = √2
Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2
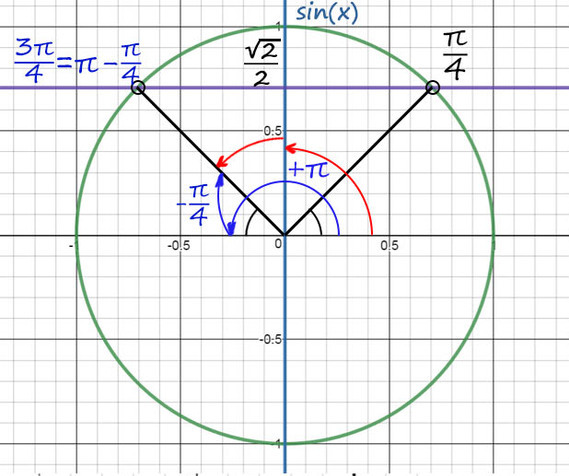
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.
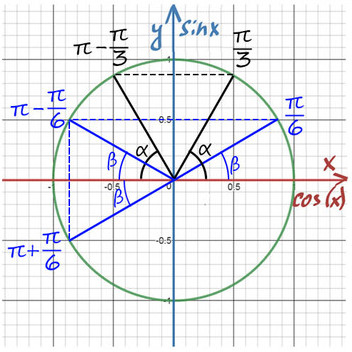
2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.
Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.
И еще не забудем добавить +2πn, n∈Ζ.
Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.
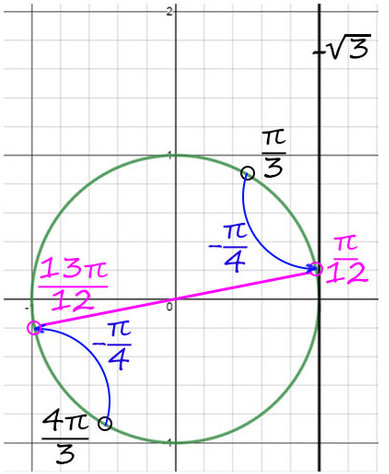
Пример №3. tg(x + π/4) = √3
Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.
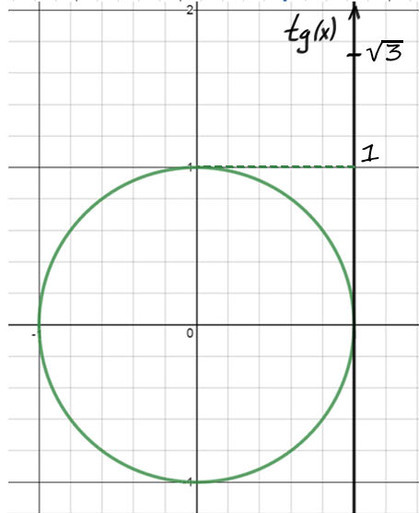
tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.
1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.
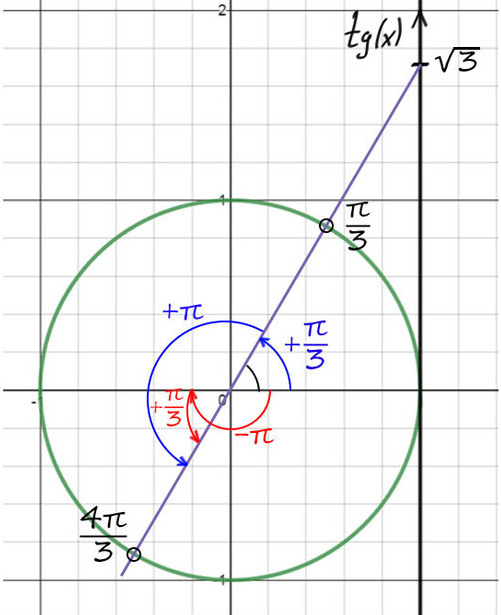
2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.
По мнемоническому правилу при тангенсе √3 первое значение — это π/3.
3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.
4) Но мы нашли только y , вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.
Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.
Теперь корни на окружности будут здесь:
Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.
Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).
Ответ можно записать и так: π/12 + πn, n∈Ζ.
Пример №4: −10ctg(x) = 10
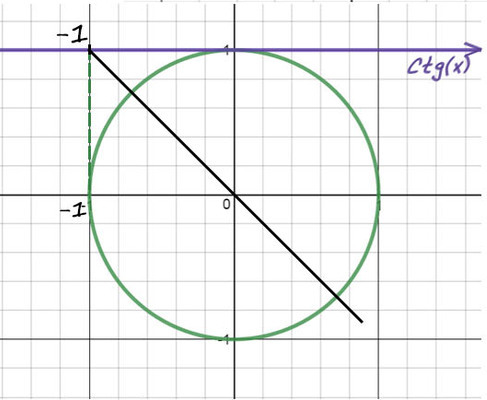
Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.
1) Проведем прямую через эту точку и начало координат.
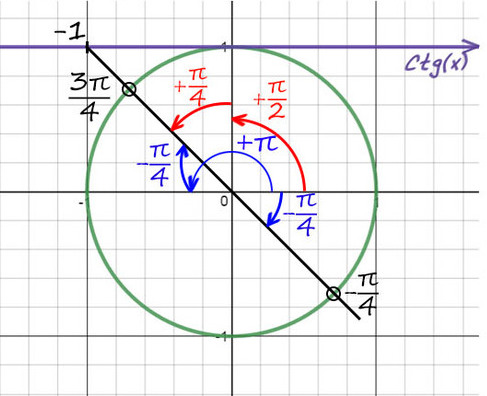
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).
Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π. ) так намного меньше шансов запутаться.
Не забываем добавить к каждой точке 2πk.
Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.
Алгоритм решения тригонометрических уравнений (на примере cos(x) = − √ 3/2) :
- Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
- Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
- Точки пересечения с окружностью и будут являться корнями уравнения.
- Значение одной точки (без разницы, как в нее попадете) +2πk.
Азов достаточно, прежде чем идти дальше закрепите полученные знания.
Видео:Решение уравнений вида tg x = a и ctg x = aСкачать
Простейшие тригонометрические уравнения. Часть 1
Простейшими называются тригонометрические уравнения следующих четырёх видов:
Любое тригонометрическое уравнение в конечном счёте сводится к решению одного или нескольких простейших. К сожалению, на этом заключительном стандартном шаге школьники часто допускают ошибки, что ведет к потере баллов на ЕГЭ. Именно поэтому так важна данная тема.
Существуют два подхода к решению простейших тригонометрических уравнений.
Первый подход — бессмысленный и тяжёлый. Следуя ему, надо выучить по шпаргалке общие формулы, а также все частные случаи. Польза от этого столь же невелика, как от зубрежки шестнадцати строк заклинаний на непонятном языке. Мы отказываемся от такого подхода раз и навсегда.
Второй подход — логический и наглядный. Для решения простейших тригонометрических уравнений мы пользуемся тригонометрическим кругом и определениями тригонометрических функций.
Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать
Уравнения и
Напомним, что — абсцисса точки на единичной окружности, соответствующей углу , а — её ордината.
Из определения синуса и косинуса следует, что уравнения и имеют решения только при условии .
Абитуриент, будь внимателен! Уравнения или решений не имеют!
Начнём с самых простых уравнений.
. .
Мы видим, что на единичной окружности имеется лишь одна точка с абсциссой 1:
Эта точка соответствует бесконечному множеству углов: . Все они получаются из нулевого угла прибавлением целого числа полных углов (т. е. нескольких полных оборотов как в одну, так и в другую сторону).
Следовательно, все эти углы могут быть записаны одной формулой:
Это и есть множество решений данного уравнения. Напоминаем, что — это множество целых чисел.
Снова видим, что на единичной окружности есть лишь одна точка с абсциссой :
Эта точка соответствует углу и всем углам, отличающихся от на несколько полных оборотов в обе стороны, т. е. на целое число полных углов. Следовательно, все решения данного уравнения записываются формулой:
. .
Отмечаем на тригонометрическом круге единственную точку с ординатой :
И записываем ответ:
Обсуждать тут уже нечего, не так ли? 🙂
Можете, кстати, записать ответ и в другом виде:
Это — дело исключительно вашего вкуса.
Заодно сделаем первое полезное наблюдение. Чтобы описать множество углов, отвечающих одной-единственной точке тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .
На тригонометрическом круге имеются две точки с ординатой 0:
Эти точки соответствуют углам Все эти углы получаются из нулевого угла прибавлением целого числа углов (т. е. с помощью нескольких полуоборотов в обе стороны). Таким образом,
Точки, лежащие на концах диаметра тригонометрического круга, мы будем называть диаметральной парой.
Точки с абсциссой 0 также образуют диаметральную пару, на сей раз вертикальную:
Все углы, отвечающие этим точкам, получаются из — прибавлением целого числа углов (полуоборотов):
Теперь мы можем сделать и второе полезное наблюдение.
Чтобы описать множество углов, отвечающих диаметральной паре точек тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .
Переходим к следующему этапу. Теперь в правой части будет стоять табличное значение синуса или косинуса (отличное от 0 или ). Начинаем с косинуса.
Имеем вертикальную пару точек с абсциссой :
Все углы, соответствующие верхней точке, описываются формулой (вспомните первое полезное наблюдение!):
Аналогично, все углы, соответствующие нижней точке, описываются формулой:
Обе серии решений можно описать одной формулой:
Остальные уравнения с косинусом решаются совершенно аналогично. Мы приводим лишь рисунок и ответ.
Теперь рассмотрим уравнения с синусом. Тут ситуация немного сложнее.
Имеем горизонтальную пару точек с ординатой :
Углы, отвечающие правой точке:
Углы, отвечающие левой точке:
Описывать эти две серии одной формулой никто не заставляет. Можно записать ответ в таком виде:
Тем не менее, объединяющая формула существует, и её надо знать. Выглядит она так:
На первый взгляд совершенно не ясно, каким образом она дает обе серии решений. Но давайте посмотрим, что получается при чётных . Если , то
Мы получили первую серию решений . А если — нечетно, , то
Это вторая серия .
Обратим внимание, что в качестве множителя при обычно ставится правая точка, в данном случае .
Остальные уравнения с синусом решаются точно так же. Мы приводим рисунок, запись ответа в виде совокупности двух серий и объединяющую формулу.
На этом с синусом и косинусом пока всё. Переходим к тангенсу.
Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать
Линия тангенсов.
Начнём с геометрической интерпретации тангенса — так называемой линии тангенсов. Это касательная к единичной окружности, параллельная оси ординат (см. рисунок).
Из подобия треугольников и имеем:
Мы рассмотрели случай, когда находится в первой четверти. Аналогично рассматриваются случаи, когда находится в остальных четвертях. В результате мы приходим к следующей геометрической интерпретации тангенса.
Тангенс угла равен ординате точки , которая является точкой пересечения линии тангенсов и прямой , соединяющей точку с началом координат.
Вот рисунок в случае, когда находится во второй четверти. Тангенс угла отрицателен.
Видео:Отбор корней по окружностиСкачать
Уравнение
Заметим, что тангенс может принимать любые действительные значения. Иными словами, уравнение имеет решения при любом .
.
Имеем диаметральную горизонтальную пару точек:
Эта пара, как мы уже знаем, описывается формулой:
Имеем диаметральную пару:
Вспоминаем второе полезное наблюдение и пишем ответ:
Остальные уравнения с тангенсом решаются аналогично. Мы приводим лишь рисунки и ответы.
На этом заканчиваем пока и с тангенсом.
Уравнение нет смысла рассматривать особо. Дело в том, что:
уравнение равносильно уравнению ;
при уравнение равносильно уравнению .
Впрочем, существует также и линия котангенсов, но. . . Об этом мы вам расскажем на занятиях 🙂
Итак, мы разобрали простейшие тригонометрические уравнения, содержащие в правой части табличные значения тригонометрических функций. Именно такие задачи встречаются в части В вариантов ЕГЭ.
А что делать, например, с уравнением ? Для этого надо сначала познакомиться с обратными тригонометрическими функциями. О них мы расскажем вам в следующей статье.
📹 Видео
Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать
ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать
Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать
Тригонометрические уравнения с помощью окружности. cosx=aСкачать
12 часов Тригонометрии с 0.Скачать
10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА 10 класс тригонометрияСкачать
Как решать тригонометрические неравенства?Скачать
Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать
Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать
ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать
Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать
Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать
