Решение уравнений с разложением многочленов на множители 7 класс видеоурок

Разделы: Математика

Ребята, достаточно долго овладевая приёмами разложения многочлена на множители, подошли к моменту, когда необходимо систематизировать и обобщить изученные способы, попытаться сделать новые открытия и самое главное: найти интересное применение разнообразных приёмов разложения на множители к решению порой одинаковых по смыслу уравнений.

1. Что, значит, разложить многочлен на множители?

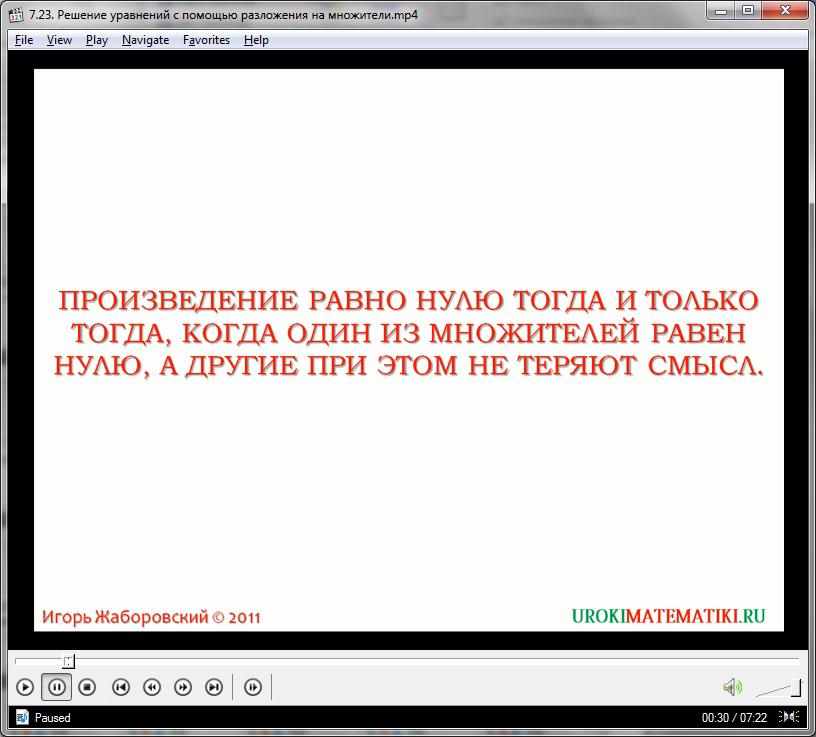
2. В каком случае произведение множителей равно 0?

3. Степень, какого числа равна нулю? 1??

4. Какие приёмы разложения на множители вам известны? (Вынесение общего множителя за скобки, группировка слагаемых с последующем вынесением общего множителя, с помощью формул сокращенного умножения).

5. Чему равны квадрат суммы, разности двух слагаемых?

6. Чему равна разность квадратов двух слагаемых?

На доске записаны уравнения:

По какому признаку можно разбить эти уравнения в группы? (Уравнения, содержащие многочлен второй степени. Уравнения, содержащие многочлен выше второй степени. Уравнение, содержащее многочлен второй степени, коэффициенты которого периодические дроби).

Нам предстоит решить эти уравнения, подбирая непохожие способы решения, несмотря порой на похожесть уравнений.

Предлагаю учащимся решить уравнение двумя способами. Вызываю к доске двух учеников.

Один ученик решает уравнение разбиением одночлена 6х на сумму двух одночленов, а другой – применением формулы сокращённого умножения – квадрата суммы:

Вопрос: Какой способ оказался более рациональным? (Конечно второй). Как его можно назвать?

(Выделение полного квадрата суммы)

Обсуждаем решение уравнения .

Можно ли решить уравнение, разбивая одно из слагаемых на два?

(да,)

А выделением полного квадрата суммы?

(затруднительно, так как, число 3 не является квадратом никакого рационального числа)

И всё-таки попробуем выделить полный квадрат суммы: дополните сумму первых двух слагаемых до квадрата суммы.

Как можно разложить многочлен в левой части уравнения на множители? (По формуле разности квадратов).

Сообразите, можно ли рассуждая аналогично решить уравнение ?

(Неудобное в данном случае число 5).

И все-таки, попробуем строго следовать формуле квадрата суммы при выделении полного квадрата:

Обратите внимание на коэффициенты уравнения . Какую закономерность можно заметить?

(Одинаково читаются слева направо)

Что происходит с показателями переменной x?

(Уменьшаются на один)

Выскажите предположение для многочлена в левой части уравнения.

(Многочлен х 4 +4х 3 +6х 2 +4х+1 есть (х+1) 4 ). Обоснуйте это.

(Построим треугольник Паскаля

14641 4-ая строка содержит коэффициенты возведения в 4-ую степень двучлена (х+1)

Итак, какой вид примет уравнение? Решите его устно.

Решите устно уравнение

Какими числами являются коэффициенты уравнения

(Периодическими десятичными дробями)

Обратите периодические дроби в обыкновенные и решите, получившееся уравнение.

(Правило обращения периодической десятичной дроби в обыкновенную: чтобы периодическую десятичную дробь обратить в обыкновенную, надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и сделать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде и после девятки дописать столько нулей, сколько цифр между запятой и первым периодом)

(Подберите рациональный способ решения и найдите корни уравнения, х=1 или )

Вновь обратимся к уравнению . Решим это уравнение методом неопределённых коэффициентов:

Сравните значения найденных корней со значениями переменных b и d. (Они противоположны)

Найденные корни подтверждают мысль о том, что независимо от способа решения корни не меняются.

Чем уравнение похоже на предыдущее?

(Коэффициент при х 2 равен 1)

Попробуем решить это уравнение устно, не применяя ни один из рассмотренных приёмов, но

принимая во внимание некоторые рассуждения в предыдущем случае:

Запишите разложение многочлена в виде произведения двучленов:

Тогда, скажите чему, будут равны значения выражений и по аналогии с предыдущими рассуждениями?

( Легко догадаться, что или наоборот).

Сообразите, чему будут равны корни уравнения?

Устно решите уравнения:

1. С каким новым способом решения квадратных уравнений вы познакомились?

(Выделение полного квадрата суммы или разности)

2. Как вы думаете, почему этот способ не всегда удобен?

(Например, в уравнении 3х 2 -2х-1=0 3х 2 не является квадратом рационального выражения)

3. Какое открытие вы сделали, применяя метод неопределённых коэффициентов для

решения квадратных уравнений, если коэффициент при равен 1?

(Чтобы найти корни, надо сначала найти два таких числа в и с, чтобы их сумма была равна второму коэффициенту, а произведение – третьему слагаемому. А корни будут равны числам, противоположным числам .

В 8 классе вы познакомитесь с ещё одним способом решения квадратных уравнений – по формулам. Узнаете, кто такой Франсуа Виет и какое отношение он имеет к нашему открытию.

Урок «Решение уравнений с помощью разложения на множители»

Краткое описание документа:

Используя законы преобразования многочленов путем вынесения общего множителя, что мы изучили на прошлых видеозанятиях, можно успешно решать уравнения различного уровня сложности. Приведем некоторые примеры.

Следует напомнить, что проводить разложение многочлена можно двумя способами. Необходимо либо находить один общий множитель и выносить его за скобки (в которых остается все выражение), либо группировать одночлены по схожим основам и уже с групп выносить множители. Кроме того, стоит усвоить правило базовой математики: произведение некоторых множителей равно нулю тогда и только тогда, когда один из множителей равен нулю, а остальные являются натуральными числами.

Рассмотрим первый пример. Дано уравнение, нужно найти его корень:

Преобразуем левую часть равенства, использовав вынесение общего множителя 5х за скобки. Получим систему уравнений, использовав правило для нулевого произведения:

Как видим, корнями уравнения являются два значения – 0 и -3.

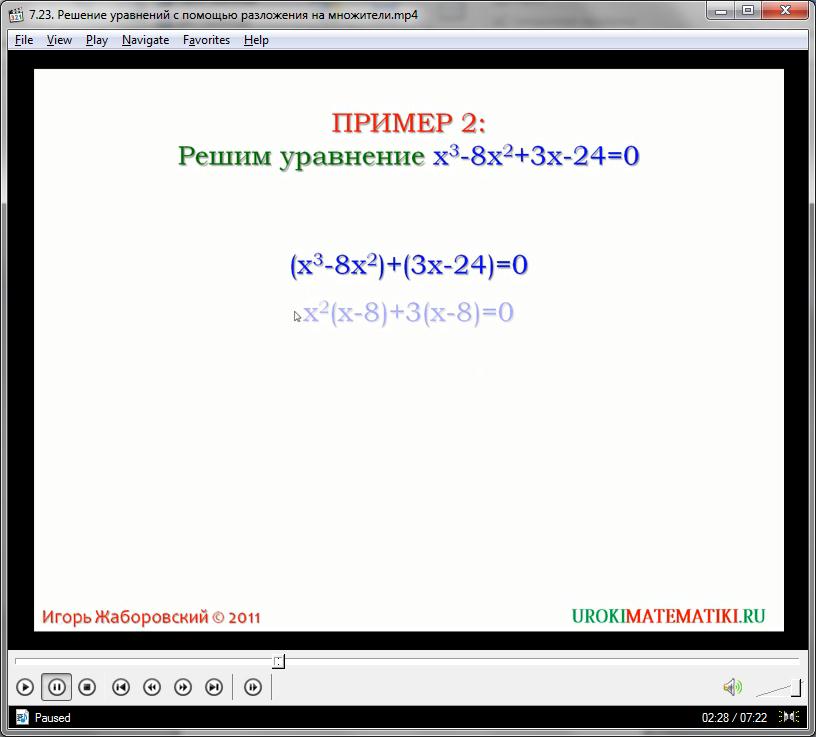
Второй пример. Необходимо решить уравнение:

х 3 – 8х 2 + 3х – 24 = 0

Используя способ группировки, получаем две группы одночленов, при этом в первой из них общее основание равно х 2 , а во второй – трем. Выносим множители за скобки:

х 3 – 8х 2 + 3х – 24 = 0

(х 3 – 8х 2 ) + (3х – 24) = 0

х 2 (х – 8) + 3(х – 8) = 0

У нас появились идентичные выражения в обеих скобках. Это позволяет представить многочлен в левой части уравнения как произведение полиномов – используя вынесение (х – 8) за скобки:

х 2 (х – 8) + 3(х – 8) = 0

Памятуя о том, что произведение любых выражений, равных нулю, возможно только тогда, когда одно из выражений равно нулю, можем записать систему уравнений, тождественных между собой, и исходящих от начального примера. Решаем эти уравнения:

Второй корень недействителен, так как квадрат его равен отрицательному числу, что противоречит закону о квадратной степени (обнуляющей минус). Поэтому корректным ответом является только первое значение переменной х, равное восьми.
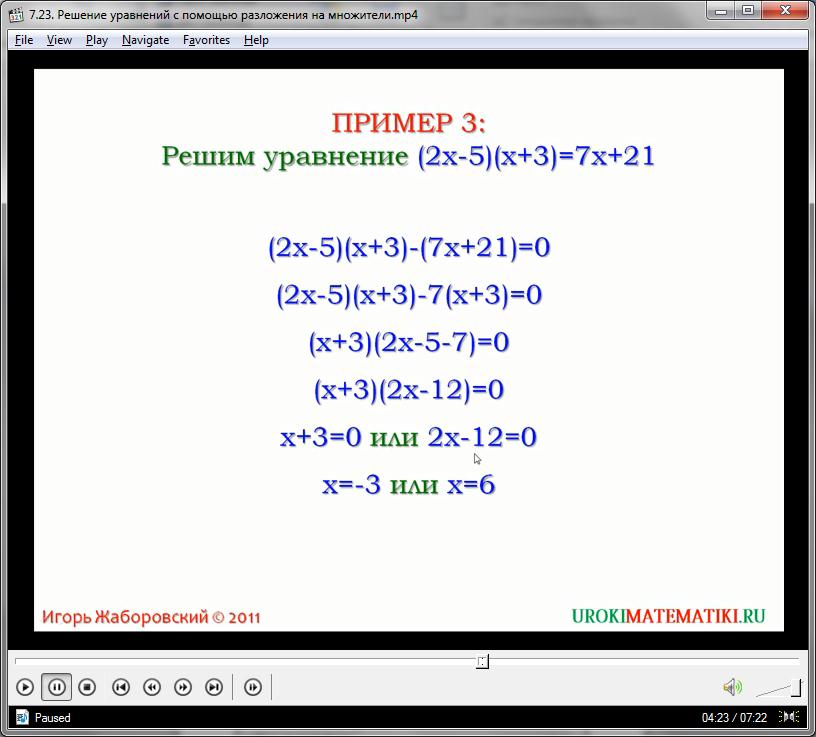
Более сложные уравнения построены так, что ни одна из частей выражения не приравнена напрямую к нулю. В этом случае следует понимать, что любое равенство можно преобразовать так, чтобы в правой части остался ноль. Законы алгебры позволяют с легкостью переносить любые элементы с одной части уравнения в другую и наоборот. Важно учитывать инверсию знаков при этой операции. Рассмотрим пример. Необходимо решить уравнение вида:

(2х – 5)(х + 3) = 7х + 21

Чтобы решить эту задачу, необходимо переместить все одночлены в левую часть, приравнивая полученный многочлен к нулю, а потом преобразовать выражение слева, образуя произведение любых подходящих множителей.

Для этого производим перемещение (7х + 21), а также вынесение семерки за скобки:

(2х – 5)(х + 3) = 7х + 21

(2х – 5)(х + 3) – 7х + 21 = 0

(2х – 5)(х + 3) – 7(х + 3) = 0

У нас появился бином, оба одночлена которого имеют общий множитель (х + 3), который выносится за скобки, образуя произведение полиномов:

(2х – 5)(х + 3) – 7(х + 3) = 0

(х + 3)(2х – 5 – 7) = 0

Решая элементарное вычитание в скобках, мы пришли к простому произведению с нулевым результатом; теперь можно решить систему уравнений:

Ответ: корнями уравнения являются числа -3 и 6.

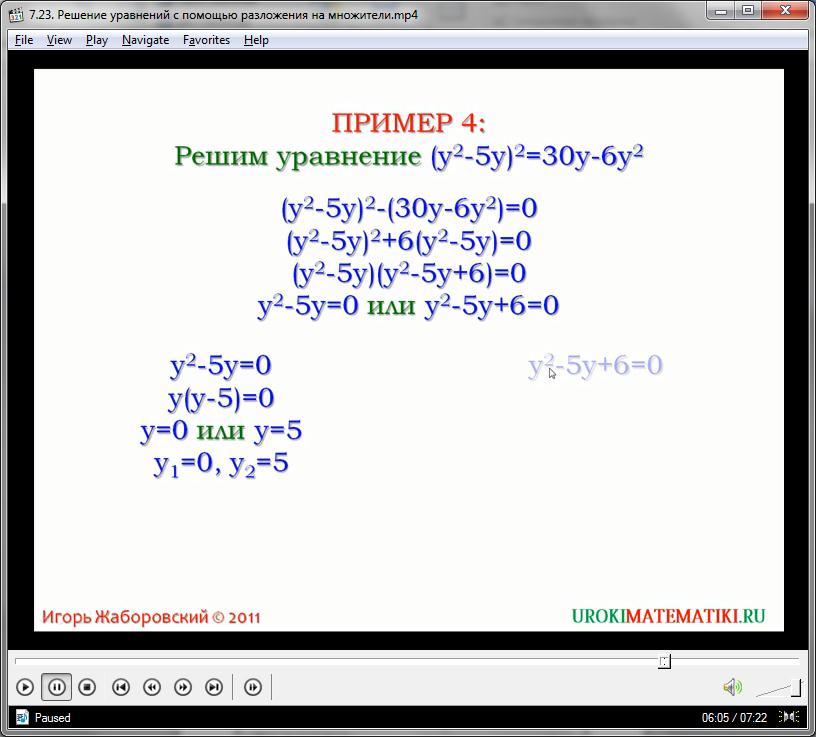
Большинство уравнений, которые изначально имеют приравнивание к нулю или которые могут быть преобразованы до подобного вида, в итоговом варианте сводятся к системе двух (иногда больше) уравнений. И очень часто ответами являются два корня. Только в случае степенных переменных корни могут быть отброшены по причине недействительности.

—> —>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Инфоурок

02.08.2014

Алгебра

Видеоурок

13809

465

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

🌟 Видео