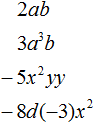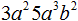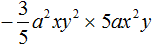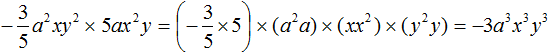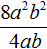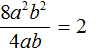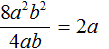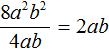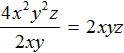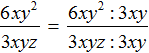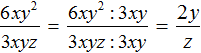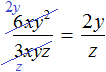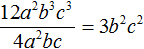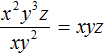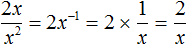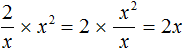- Определения и примеры
- Приведение одночлена к стандартному виду
- Сложение и вычитание одночленов
- Умножение одночленов
- Деление одночленов
- Возведение одночлена в степень
- Разложение одночлена на множители
- Урок по алгебре в 7-м классе по теме: «Решение уравнений с применением приемов разложения многочлена на множители»
- Деление одночлена на одночлен
- 🔥 Видео
Видео:7 класс// АЛГЕБРА // Умножение одночлена на многочлен, решение уравненийСкачать

Определения и примеры
Одночлен — это произведение чисел, переменных и степеней. Например, выражения 5a , 3ab 2 и −6 2 aa 2 b 3 являются одночленами.
Приведём ещё примеры одночленов:
Одночленом также является любое отдельное число, любая переменная или любая степень. Например, число 9 является одночленом, переменная x является одночленом, степень 5 2 является одночленом.
Видео:Произведение одночлена и многочлена. Умножение одночлена и многочлена. 7 класс.Скачать
Приведение одночлена к стандартному виду
Рассмотрим следующий одночлен:
Этот одночлен выглядит не очень аккуратно. Чтобы сделать его проще, нужно привести его к так называемому стандартному виду.
Приведение одночлена к стандартному виду заключается в перемножении однотипных сомножителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему.
Ещё один нюанс заключается в том, что в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.
Итак, приведём одночлен 3a 2 5a 3 b 2 к стандартному виду. В этом одночлене содержатся числа 3 и 5. Перемножим их, получим число 15. Записываем его:
Далее в одночлене 3a 2 5a 3 b 2 содержатся степени a 2 и a 3 , которые имеют одинаковое основание a . Из тождественных преобразований со степенями известно, что при перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают. Тогда перемножение степеней a 2 и a 3 даст в результате a 5 . Записываем a 5 рядом с числом 15
Далее в одночлене 3a 2 5a 3 b 2 содержится степень b 2 . Её не с чем перемножать, поэтому она остаётся без изменений. Записываем её как есть к новому одночлену:
Мы привели одночлен 3a 2 5a 3 b 2 к стандартному виду. В результате получили одночлен 15a 5 b 2
Числовой сомножитель 15 называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.
Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице. Так, коэффициентом одночлена abc является 1, поскольку abc это произведение единицы и abc
А коэффициентом одночлена −abc будет −1 , поскольку −abc это произведение минус единицы и abc
Степенью одночлена называют сумму показателей всех переменных входящих в этот одночлен.
Например, степенью одночлена 15a 5 b 2 является 7 . Это потому что переменная a имеет показатель 5, а переменная b имеет показатель 2. Отсюда 5 + 2 = 7 . Показатель числового сомножителя 15 считать не нужно, поскольку нас интересуют только показатели переменных.
Ещё пример. Степенью одночлена 7ab 2 является 3. Здесь переменная a имеет показатель 1, а переменная b имеет показатель 2. Отсюда 1 + 2 = 3 .
Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю. Например, степень одночлена 11 равна нулю.
Не следует путать степень одночлена и степень числа. Степень числа это произведение из нескольких одинаковых множителей, тогда как степень одночлена это сумма показателей всех переменных входящих в этот одночлен. В одночлене 11 нет переменных, поэтому его степень равна нулю.
Пример 1. Привести одночлен 5xx3ya 2 к стандартному виду
Перемножим числа 5 и 3, получим 15. Это будет коэффициент одночлена:
Далее в одночлене 5xx3ya 2 содержатся переменные x и x . Перемножим их, получим x 2 .
Далее в одночлене 5xx3ya 2 содержится переменная y , которую не с чем перемножать. Записываем её без изменений:
Далее в одночлене 5xx3ya 2 содержится степень a 2 , которую тоже не с чем перемножать. Её также оставляем без изменений:
Получили одночлен 15x 2 ya 2 , который приведён к стандартному виду. Буквенные сомножители принято записывать в алфавитном порядке. Тогда одночлен 15x 2 ya 2 примет вид 15a 2 x 2 y.
Пример 2. Привести одночлен 2m 3 n × 0,4mn к стандартному виду
Перемножим числа, переменные и степени по отдельности.
Числа, переменные и степени при перемножении разрешается заключать в скобки. Делается это для удобства. Так, в данном примере перемножение чисел 2 и 0,4 можно заключить в скобки. Также в скобки можно заключить перемножение m 3 × m и n × n
Но желательно выполнять все элементарные действия в уме. Так, решение можно записать значительно короче:
Но чтобы в уме приводить одночлен к стандартному виду, тема умножения целых чисел и умножения степеней должна быть изучена на хорошем уровне.
Видео:Одночлены. 7 класс.Скачать

Сложение и вычитание одночленов
Одночлены можно складывать и вычитать. Чтобы это было возможно, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути приведение подобных слагаемых, которое мы рассматривали при изучении буквенных выражений.
Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.
Пример 1. Сложить одночлены 6a 2 b и 2a 2 b
Сложим коэффициенты 6 и 2, а буквенную часть 6a 2 b оставим без изменений
Пример 2. Вычесть из одночлена 5a 2 b 3 одночлен 2a 2 b 3
Можно заменить вычитание сложением, и сложить коэффициенты одночленов, оставив буквенную часть без изменения:
Либо сразу из коэффициента первого одночлена вычесть коэффициент второго одночлена, а буквенную часть оставить без изменения:
Видео:Алгебра 7 класс с нуля | Математика | УмскулСкачать

Умножение одночленов
Одночлены можно перемножать. Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.
Пример 1. Перемножить одночлены 5x и 8y
Перемножим числовые и буквенные части по отдельности. Для удобства перемножаемые сомножители будем заключать в скобки:
Пример 2. Перемножить одночлены 5x 2 y 3 и 7x 3 y 2 c
Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:
Пример 3. Перемножить одночлены −5a 2 bc и 2a 2 b 4
Пример 4. Перемножить одночлены x 2 y 5 и (−6xy 2 )
Пример 5. Найти значение выражения
Видео:Многочлены. 7 класс.Скачать

Деление одночленов
Одночлен можно разделить на другой одночлен. Для этого нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.
Например, разделим одночлен 8a 2 b 2 на одночлен 4ab. Запишем это деление в виде дроби:
Первый одночлен 8a 2 b 2 будем называть делимым, а второй 4ab — делителем. А одночлен, который получится в результате, назовём частным.
Разделим коэффициент делимого на коэффициент делителя, получим 8 : 4 = 2 . В исходном выражении ставим знак равенства и записываем этот коэффициент частного:
Теперь делим буквенную часть. В делимом содержится a 2 , в делителе — просто a . Делим a 2 на a , получаем a , поскольку a 2 : a = a 2 − 1 = a . Записываем в частном a после 2
Далее в делимом содержится b 2 , в делителе — просто b . Делим b 2 на b , получаем b , поскольку b 2 : b = b 2 − 1 = b . Записываем в частном b после a
Значит, при делении одночлена 8a 2 b 2 на одночлен 4ab получается одночлен 2ab .
Сразу можно выполнить проверку. При умножении частного на делитель должно получаться делимое. В нашем случае, если 2ab умножить на 4ab , должно получиться 8a 2 b 2
Не всегда можно первый одночлен разделить на второй одночлен. Например, если в делителе окажется переменная, которой нет в делимом, то говорят, что деление невозможно.
К примеру, одночлен 6xy 2 нельзя разделить на одночлен 3xyz . В делителе 3xyz содержится переменная z , которая не содержится в делимом 6xy 2 .
Проще говоря, мы не сможем найти частное, которое при умножении на делитель 3xyz дало бы делимое 6xy 2 , поскольку такое умножение обязательно будет содержать переменную z, которой нет в 6xy 2 .
Но если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.
Например, при делении одночлена 4x 2 y 2 z на 2xy , получается 2xyz . Сначала разделили 4 на 2 получили 2, затем x 2 разделили на x , получили x , затем y 2 разделили на y , получили y. Затем приступили к делению переменной z на такую же переменную в делителе, но обнаружили, что такой переменной в делителе нет. Поэтому перенесли переменную z в частное без изменений:
Для проверки умножим частное 2xyz на делитель 2xy . В результате должен получиться одночлен 4x 2 y 2 z
Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.
Так, в предыдущем примере нельзя было разделить одночлен 6xy 2 на одночлен 3 xyz . Но можно сократить эту дробь на одночлен 3xy . Напомним, что сокращение дроби это деление числителя и знаменателя на одно и то же число (в нашем случае на одночлен 3 xy ). В результате сокращения дробь становится проще, но её значение не меняется:
В числителе и знаменателе мы пришли к делению одночленов, которое можно выполнить:
Процесс деления обычно выполняется в уме, записывая над числителем и знаменателем получившийся результат:
Пример 2. Разделить одночлен 12a 2 b 3 c 3 на одночлен 4a 2 bc
Пример 3. Разделить одночлен x 2 y 3 z на одночлен xy 2
Дополнительно упомянем, что деление одночлена на одночлен также невозможно, если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя.
Например, разделить одночлен 2x на одночлен x 2 нельзя, поскольку степень x , входящая в делимое, имеет показатель 1, тогда как степень x 2 , входящая в делитель, имеет показатель 2. Мы не сможем найти частное, которое при перемножении с делителем x 2 даст в результате делимое 2x .
Конечно, мы можем выполнить деление x на x 2 , воспользовавшись свойством степени с целым показателем:
и такое частное при перемножении с делителем x 2 будет давать в результате делимое 2x
Но нас пока интересуют только те частные, которые являются так называемыми целыми выражениями. Целые выражения это те выражения, которые не являются дробями, в знаменателе которых содержится буквенное выражение. А частное 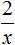
Видео:Одночлены. Практическая часть - решение примеров. 7 класс.Скачать

Возведение одночлена в степень
Одночлен можно возвести в степень. Для этого используют правило возведения степени в степень.
Пример 1. Возвести одночлен xy во вторую степень.
Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый сомножитель этого одночлена
Пример 2. Возвести одночлен −5a 3 b во вторую степень.
Пример 3. Возвести одночлен − a 2 bc 3 в пятую степень.
В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень:
Когда коэффициент равен −1, то саму единицу не записывают. Записывают только минус и потом остальные сомножители одночлена. В приведенном примере сначала получился одночлен −1a 10 b 5 c 15 , затем он был заменён на тождественно равный ему одночлен −a 10 b 5 c 15 .
Пример 4. Представить одночлен 4x 2 в виде одночлена, возведённого в квадрат.
В данном примере нужно найти произведение, которое во второй степени будет равно выражению 4x 2 . Очевидно, что это произведение 2x. Если это произведение возвести во вторую степень (в квадрат), то получится 4x 2
Значит, 4x 2 = (2x) 2 . Выражение (2x) 2 это и есть одночлен, возведённый в квадрат.
Пример 5. Представить одночлен 121a 6 в виде одночлена, возведённого в квадрат.
Попробуем найти произведение, которое во второй степени будет равно выражению 121a 6 .
Прежде всего заметим, что число 121 получается, если число 11 возвести в квадрат. То есть первый сомножитель будущего произведения мы нашли. А степень a 6 получается в том случае, если возвести в квадрат степень a 3 . Значит вторым сомножителем будущего произведения будет a 3 .
Таким образом, если произведение 11a 3 возвести во вторую степень, то получится 121a 6
(11a 3 ) 2 = 11 2 × (a 3 ) 2 = 121a 6
Значит, 121a 6 = (11a 3 ) 2 . Выражение (11a 3 ) 2 это и есть одночлен, возведённый в квадрат.
Видео:Одночлен и его стандартный вид. Алгебра, 7 классСкачать

Разложение одночлена на множители
Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.
Пример 1. Разложить одночлен 3a 3 b 2 на множители
Данный одночлен можно разложить на множители 3, a, a, a, b, b
Либо степень b 2 можно не раскладывать на множители b и b
Либо степень b 2 разложить на множители b и b , а степень a 3 оставить без изменений
В каком виде представлять одночлен зависит от решаемой задачи. Главное, чтобы разложение было тождественно равно исходному одночлену.
Пример 2. Разложить одночлен 10a 2 b 3 c 4 на множители.
Разложим коэффициент 10 на множители 2 и 5, степень a 2 разложим на множители aa , степень b 3 — на множители bbb , степень c 4 — на множители cccc
Видео:Алгебра 7 класс (Урок№21 - Произведение одночлена и многочлена.)Скачать

Урок по алгебре в 7-м классе по теме: «Решение уравнений с применением приемов разложения многочлена на множители»
Разделы: Математика
Ребята, достаточно долго овладевая приёмами разложения многочлена на множители, подошли к моменту, когда необходимо систематизировать и обобщить изученные способы, попытаться сделать новые открытия и самое главное: найти интересное применение разнообразных приёмов разложения на множители к решению порой одинаковых по смыслу уравнений.
1. Что, значит, разложить многочлен на множители?
2. В каком случае произведение множителей равно 0?
3. Степень, какого числа равна нулю? 1?
4. Какие приёмы разложения на множители вам известны? (Вынесение общего множителя за скобки, группировка слагаемых с последующем вынесением общего множителя, с помощью формул сокращенного умножения).
5. Чему равны квадрат суммы, разности двух слагаемых?
6. Чему равна разность квадратов двух слагаемых?
На доске записаны уравнения:
По какому признаку можно разбить эти уравнения в группы? (Уравнения, содержащие многочлен второй степени. Уравнения, содержащие многочлен выше второй степени. Уравнение, содержащее многочлен второй степени, коэффициенты которого периодические дроби).
Нам предстоит решить эти уравнения, подбирая непохожие способы решения, несмотря порой на похожесть уравнений.
Предлагаю учащимся решить уравнение 
Один ученик решает уравнение разбиением одночлена 6х на сумму двух одночленов
Вопрос: Какой способ оказался более рациональным? (Конечно второй). Как его можно назвать?
(Выделение полного квадрата суммы)
Обсуждаем решение уравнения 
Можно ли решить уравнение, разбивая одно из слагаемых на два?
(да,
А выделением полного квадрата суммы?
(затруднительно, так как, число 3 не является квадратом никакого рационального числа)
И всё-таки попробуем выделить полный квадрат суммы: дополните сумму первых двух слагаемых до квадрата суммы.
Как можно разложить многочлен в левой части уравнения на множители? (По формуле разности квадратов).
Сообразите, можно ли рассуждая аналогично решить уравнение 
(Неудобное в данном случае число 5).
И все-таки, попробуем строго следовать формуле квадрата суммы при выделении полного квадрата:
Обратите внимание на коэффициенты уравнения 
(Одинаково читаются слева направо)
Что происходит с показателями переменной x?
(Уменьшаются на один)
Выскажите предположение для многочлена в левой части уравнения.
(Многочлен х 4 +4х 3 +6х 2 +4х+1 есть (х+1) 4 ). Обоснуйте это.
(Построим треугольник Паскаля
14641 4-ая строка содержит коэффициенты возведения в 4-ую степень двучлена (х+1)
Итак, какой вид примет уравнение? Решите его устно.
Решите устно уравнение
Какими числами являются коэффициенты уравнения
(Периодическими десятичными дробями)
Обратите периодические дроби в обыкновенные и решите, получившееся уравнение.
(Правило обращения периодической десятичной дроби в обыкновенную: чтобы периодическую десятичную дробь обратить в обыкновенную, надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и сделать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде и после девятки дописать столько нулей, сколько цифр между запятой и первым периодом)
(Подберите рациональный способ решения и найдите корни уравнения, х=1 или 
Вновь обратимся к уравнению 
Сравните значения найденных корней со значениями переменных b и d. (Они противоположны)
Найденные корни подтверждают мысль о том, что независимо от способа решения корни не меняются.
Чем уравнение 
(Коэффициент при х 2 равен 1)
Попробуем решить это уравнение устно, не применяя ни один из рассмотренных приёмов, но
принимая во внимание некоторые рассуждения в предыдущем случае:
Запишите разложение многочлена 
Тогда, скажите чему, будут равны значения выражений 

( 

Сообразите, чему будут равны корни уравнения?
Устно решите уравнения:
1. С каким новым способом решения квадратных уравнений вы познакомились?
(Выделение полного квадрата суммы или разности)
2. Как вы думаете, почему этот способ не всегда удобен?
(Например, в уравнении 3х 2 -2х-1=0 3х 2 не является квадратом рационального выражения)
3. Какое открытие вы сделали, применяя метод неопределённых коэффициентов для
решения квадратных уравнений, если коэффициент при 
(Чтобы найти корни, надо сначала найти два таких числа в и с, чтобы их сумма была равна второму коэффициенту, а произведение – третьему слагаемому. А корни будут равны числам, противоположным числам 
В 8 классе вы познакомитесь с ещё одним способом решения квадратных уравнений – по формулам. Узнаете, кто такой Франсуа Виет и какое отношение он имеет к нашему открытию.
Видео:Умножение одночлена на многочлен. Алгебра, 7 классСкачать

Деление одночлена на одночлен
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке мы повторим операцию умножения одночленов, свойства степеней и сокращение дробей. Дадим определение операции деления одночлена на одночлен. Рассмотрим примеры.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Упрощение выражений»
🔥 Видео
7 класс, 16 урок, Понятие одночлена. Стандартный вид одночленаСкачать

Задание №1 "Упростить выражение" по теме "Умножение и сложение многочленов и одночленов". Алгебра 7Скачать

Сложение и вычитание многочленов. Алгебра, 7 классСкачать

Произведение многочленов. 7 класс.Скачать

Умножение одночленов. Возведение одночлена в степень. Алгебра, 7 классСкачать

Алгебра 7 класс (Урок№15 - Понятие одночлена.)Скачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

7 класс// АЛГЕБРА // Умножение многочленов. Решение уравненийСкачать

Уравнения с дробями. Алгебра 7 класс.Скачать

7 класс// АЛГЕБРА // Умножение одночлена на многочлен, решение задачСкачать