- Правило раскрытия скобок при сложении
- Правило раскрытия скобок при сложении.
- Правило раскрытия скобок при вычитании
- Раскрытие скобок при умножении
- Скобка на скобку
- Скобка в скобке
- Раскрытие скобок при делении
- Раскрытие скобок
- Понятие раскрытия скобок
- Первое правило раскрытия скобок
- Второе правило раскрытия скобок
- Другие правила раскрытия скобок
- Таблица с формулами раскрытия скобок
- Скобка в скобке
- Порядок раскрытия скобок
- Задачи для самостоятельного решения
- Раскрытие скобок: правила и примеры
- Раскрытие скобок: правила
- Правило раскрытия скобок при сложении
- Правило раскрытия скобок при вычитании
- Раскрытие скобок при умножении
- Раскрытие скобок при делении
- Раскрытие скобок при умножении двух скобок
- Раскрытие вложенных скобок
- Раскрытие скобок в натуральной степени
- 📽️ Видео
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Правило раскрытия скобок при сложении
Раскрытие скобок — это избавление выражений от скобок и изменение порядка вычислений.
Существует 4 правила раскрытия скобок при:
Видео:Раскрытие скобок. 6 класс.Скачать

Правило раскрытия скобок при сложении.
При раскрытии скобок в выражении используется сочетательное свойство сложения, которое гласит:
Если к числу нужно прибавить сумму двух чисел, то можно к этому числу прибавить сначала первое слагаемое, а затем второе.
a + (b +c) = a + b + c
Применяя это свойство, следует придерживаться следующего правила раскрытия скобок:
Если перед скобками стоит знак «+», все числа, которые стоят внутри скобок, сохраняют свой знак.
a + (b + c) = a + b + c
a + (b – c) = a + b – c
a + (-b + c) = a – b + c
a + (-b – c) = a – b – c
Это же правило применяется, когда в выражении встречается две или более скобки.
a + (b – c) + d + (-f) = a + b — c + d – f
Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Правило раскрытия скобок при вычитании
Если перед скобками стоит знак «–», то при их раскрытии следует знаки слагаемых поменять на противоположные.
a – (b + c) = a – b– c
a – (b – c) = a – b + c
a – (-b + c) = a + b – c
a – (-b – c) = a + b + c
Когда в скобках перед первым слагаемым знак отсутствует, то это означает, что оно положительное и при раскрытии скобок становится отрицательным.
Решение подобных примеров состоит из действий:
- раскрываются скобки;
- меняется знак каждого слагаемого на противоположный.
x – (y + z) = x – y – z;
m – (-n – p) = m + n + p;
Случаи, когда в выражении присутствуют сложение и вычитание скобок.
10a + (19b – 34c) – 50 – (m + n)
В данном примере скобки раскрываются по алгоритму:
- к первой скобке применяется правило сложения;
- вторая скобка раскрывается правилом вычитания.
10a + 19b – 34 c – 50 – m – n
Раскрытие скобок в сложных выражениях.
Сложное выражение — это выражение, в котором используются скобки и знаки деление/умножение.
Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Раскрытие скобок при умножении
Действия по раскрытию скобок при умножении строятся на основании работы распределительного или сочетательного свойства умножения.
Применение того или иного свойства умножения зависит от действия внутри скобок. Если это сложение или вычитание, работает распределительное свойство. При умножении или делении применяется сочетательное свойство.
1. Раскрытие скобок, согласно распределительному свойству.
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.
a ∙ (b + c) = ab + ac
(a + b) ∙ c = ac + bc
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.
a ∙ (b – c) = ab – ac
(a – b) ∙ c = ac − bc
В математике для сокращения записей знак умножения перед числом и скобкой не ставится.
Если общий множитель является отрицательной величиной, то все значения в скобках умножаются на (–1) и меняют свои знаки на противоположные:
2. Раскрытие скобок, согласно сочетательному свойству:
Произведение трех и более множителей не изменится, если эту группу множителей заменить их произведением.
(a ∙ b) ∙ c = a ∙ b ∙ c
(b ∙ c ∙ d) ∙ a = b ∙ c ∙ d ∙ a
В случае, когда в скобках выполняется умножение, раскрытие происходит как при сложении — просто раскрываются скобки и все значения перемножаются:
a ∙ (b ∙ c) = a ∙ b ∙ c
(b ∙ c) ∙ а = b ∙ c ∙ a
При раскрытии скобок необходимо учитывать правило знаков.
При делении внутри скобок, раскрытие происходит следующим образом:
Когда общий множитель находится перед скобками, то:
- общий множитель умножается на первое число в скобках и делится на второе число:
a ⋅ (b : с) = a ⋅ b : с;
- или общий множитель делится на второе число в скобках и умножается на первое число:
a ⋅ (b : с) = a : c ⋅ b.
Когда общий множитель находится после скобок, то:
- общий множитель умножается на первое число в скобках и делится на второе:
(a : b) ⋅c = с ⋅ a : b;
- общий множитель делится на второе число в скобках и умножается на первое:
(a : b) ⋅ c =с : b ⋅ a.
Скобка на скобку
Когда требуется перемножить несколько скобок друг на друга, нужно каждый член первой скобки умножить на каждый член второй скобки:
(a + b) ⋅ (c – d) = a ⋅ (c – d) + b ⋅ (c – d) = ac – ad + bc – bd
Алгоритм действий при раскрытии скобки на скобку:
- Первая скобка раскрывается, каждое ее слагаемое умножается на вторую скобку.
- Выполняется умножение числа на скобку, приводятся подобные слагаемые.
( 5 х + 7 ) ⋅ ( 10 x – 2 ) =
5 х ( 10 x – 2 ) + 7 ( 10 x – 2 ) =
50 х ² – 10 х + 70 х – 14 =
Скобка в скобке
В математике могут встречаться примеры, когда скобки входят в другие скобки.
Алгоритм действий такого типа примеров:
- Последовательно раскрывается каждая скобка, начиная с внутренней.
- Скобки раскрываются согласно принятым правилам раскрытия скобок при сложении, вычитании, умножении и делении.
- Приводятся подобные слагаемые для дальнейшего решения математического выражения или уравнения
8x + y(4 – (2x – y)) = 8x + y(4 – 2x + y) = 8x + 4y – 2xy + y²
Видео:Уравнения со скобками - 5 класс (примеры)Скачать

Раскрытие скобок при делении
- Случаи, когда в скобках выполняется сложение или вычитание.
Правило 5
Если знак деления стоит после скобок — каждое число внутри скобок делится на делитель, который стоит после скобок:
(a + b) : c = a : c + b : c;
(a – b) : c = a: c – b : c.
Если знак деления стоит перед скобками, то делимое делится на каждое число в скобках:
c : (a + b) = c : a + c : b;
c : (a – b) = c : a – c : b.
- В случае, когда в скобках выполняется умножение, то:
Если знак деления стоит перед скобкой:
- делимое делится на первое число в скобках и делится на второе:
a : (b ⋅ c) = a : b : c;
- или делимое делится на второе число в скобках, а потом делится на первое:
a : (b ⋅ c) = a : c : b.
Если знак деления стоит после скобки:
- первое число в скобках делится на делитель и умножается на второе:
(b ⋅ c) : a = (b : a) ⋅ c ;
- или второе число в скобках делится на делитель и умножается на первое:
(b ⋅ c) : a = (c : a) ⋅ b .
Если внутри скобок выполняется деление:
- делимое делится на первое число внутри скобки и умножается на второе:
a : (b : c) = a : b ⋅ c;
- первое число в скобках делится на делитель и делится на второе число:
(b : с) : a = b : c : a.
Не забываем, что при раскрытии скобок необходимо учитывать правило знаков, описанное выше:
Видео:Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Раскрытие скобок
О чем эта статья:
Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Понятие раскрытия скобок
В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.
Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.
Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:
Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.
Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.
В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:
- знаки плюс или минус перед скобками, которые заключают сумму или разность, например, (a + 7) и -(-3 + 2a — 12 — b);
- произведение числа, одной или нескольких букв и суммы или разности в скобках, например, 3(2 — 7), (3 — a + 8c)(-b) или -2a(b + 2c — 3m).
Раскрытие скобок также можно рассматривать шире.
Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:
Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:
Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.
Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:
- 5 — (3 — (2 — 1)) = 5 — (3 — 2 + 1) = 5 — 3 + 2 — 1
Видео:Решение уравнений, 6 классСкачать

Первое правило раскрытия скобок
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.
Первое правило раскрытия скобок
Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.
Формула раскрытия скобок
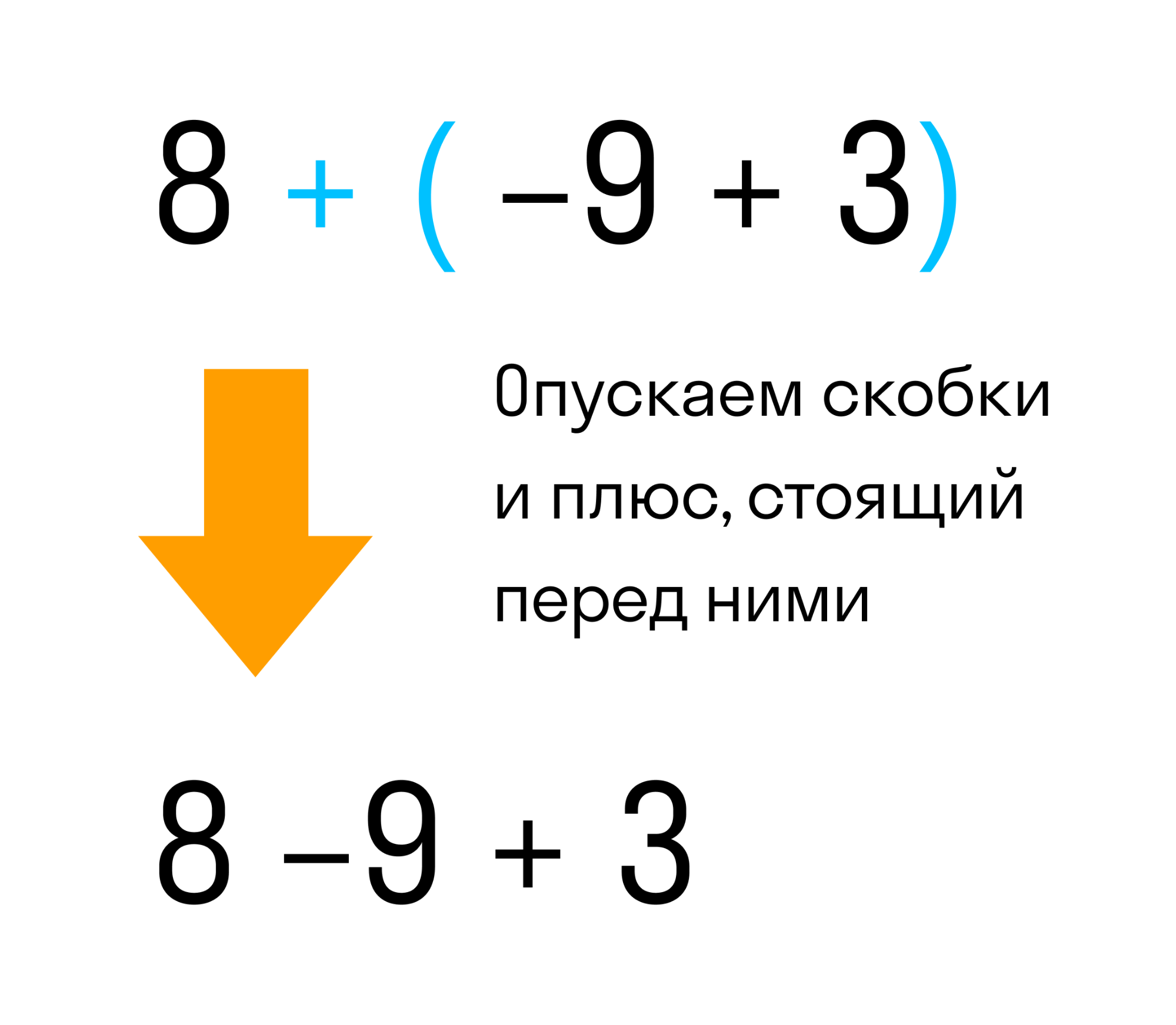
Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:
Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.
Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:
Потренируемся применять правило на примерах.
Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)
Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:
Пример 2. Раскрыть скобки в выражении 6 + (−2)
Перед скобками стоит плюс, значит применим то же правило:
Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.
В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.
Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.
Идем дальше. Теперь упростим выражение 2a + a − 5b + b.
Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:
- 2a + a — 5b + b = 2a + a + (-5b) + b = (2 + 1) * a + (-5 + 1) * b = 3a + (-4b)
Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.
Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.
После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:
Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:
- 2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6
Пример 3. Раскрыть скобки 6 + (−3) + (−2)
В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:
Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.
Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.
Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:
- 1 + (2 + 3 − 4) = 1 + 2 + 3 − 4
Пример 4. Раскрыть скобки в выражении (−7)
Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:
Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)
Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Второе правило раскрытия скобок
Здесь рассмотрим второе правило раскрытия скобок. Звучит так:
Второе правило раскрытия скобок
Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.
Формула раскрытия скобок
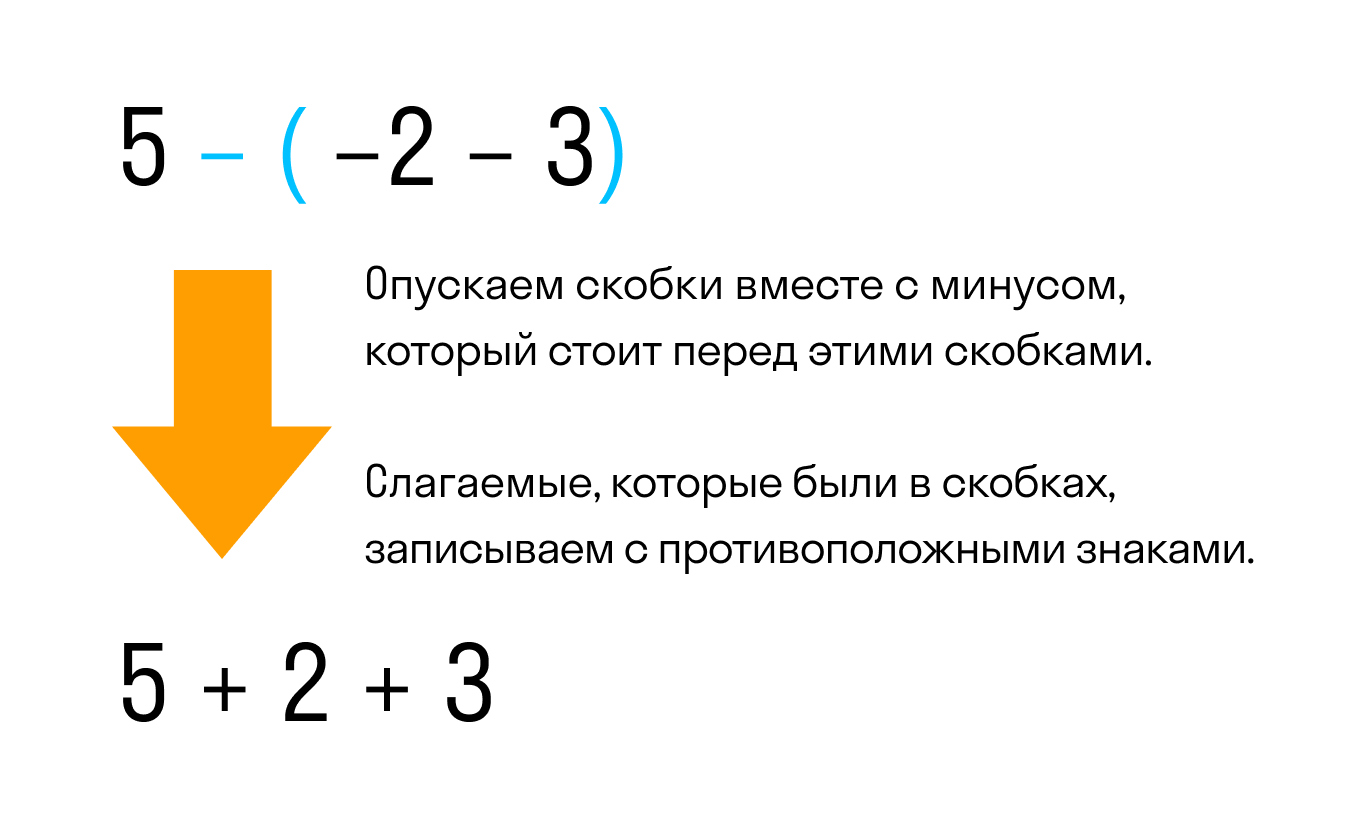
Например, раскроем скобки в выражении 5 − (−2 − 3)
Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:
Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.
Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:
Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
18 − (−1 − 5) = 18 + 1 + 5
Пример 2. Раскрыть скобки −(−6 + 7)
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)
Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:
−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2
Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
a − (3b + 3) + 10 = a − 3b − 3 + 10
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Другие правила раскрытия скобок
Правило раскрытия скобок при делении
Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.
Формула раскрытия скобок
(a + b) : c = a/c + b/c.
Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.
Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.
Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:
Далее умножим скобку на число:
- (x + 2) * 3/2 = x * 3/2 + 2 * 3/2.

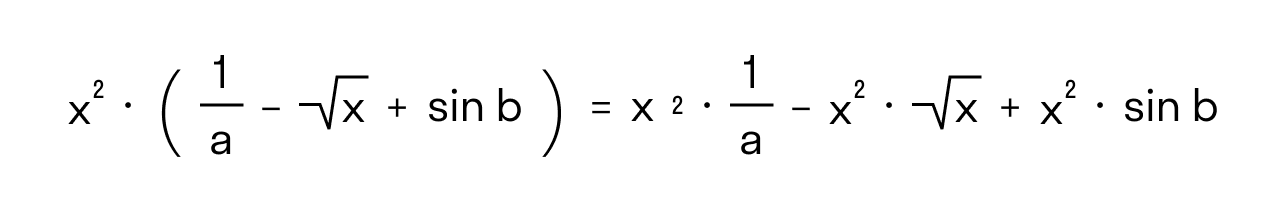







 Раскрытие скобок и правила применения – это одна из основных тем математике, на базе которой решаются многие задания во всех последующих классах. Поэтому правила раскрытия скобок необходимо усвоить в обязательном порядке.
Раскрытие скобок и правила применения – это одна из основных тем математике, на базе которой решаются многие задания во всех последующих классах. Поэтому правила раскрытия скобок необходимо усвоить в обязательном порядке.



