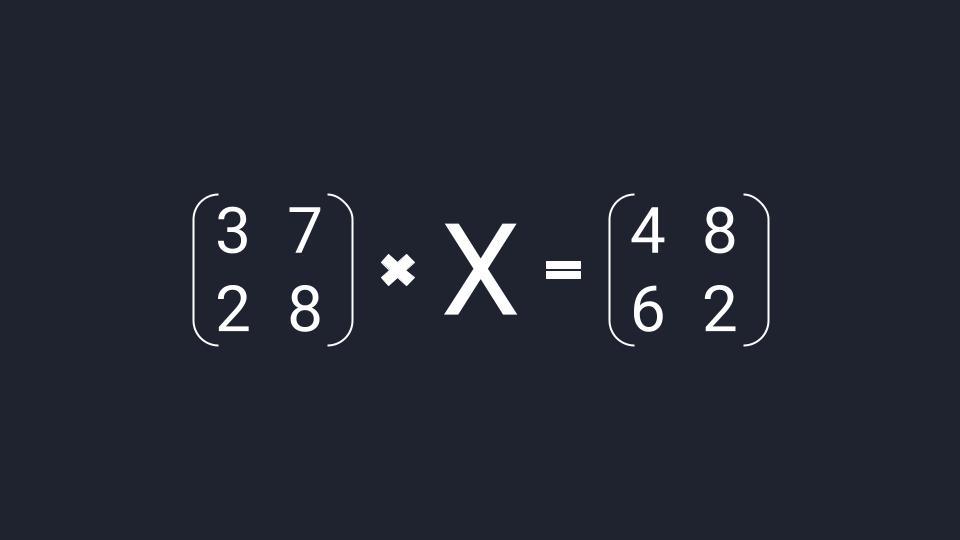Финальная глава саги.
Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».
Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.
Краткое содержание прошлых частей:
- Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
- Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
- Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
- Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
- Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
- Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.
И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.
❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.
- Что такое матричное уравнение
- Шаг 1. Упрощаем уравнение
- Шаг 2. Вводим единичную матрицу
- Шаг 3. Находим обратную матрицу
- Шаг 4. Вычисляем неизвестную матрицу
- Шаг 5. Проверяем уравнение
- Ну и что
- Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы
- Пример решения системы линейных уравнений с помощью метода обратной матрицы
- Решение матриц методы решений и примеров для чайников, формулы вычислений и действий с матрицами
- Понятие выражения
- Сложение и вычитание
- Умножение на число
- Операция перемножения
- Возведение в степень
- Расчёт определителя
- Обратная матрица
- Нахождение собственных векторов
- Метод Гаусса
- Способ Крамера
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Что такое матричное уравнение
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
Видео:Решение матричных уравненийСкачать

Шаг 1. Упрощаем уравнение
Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.
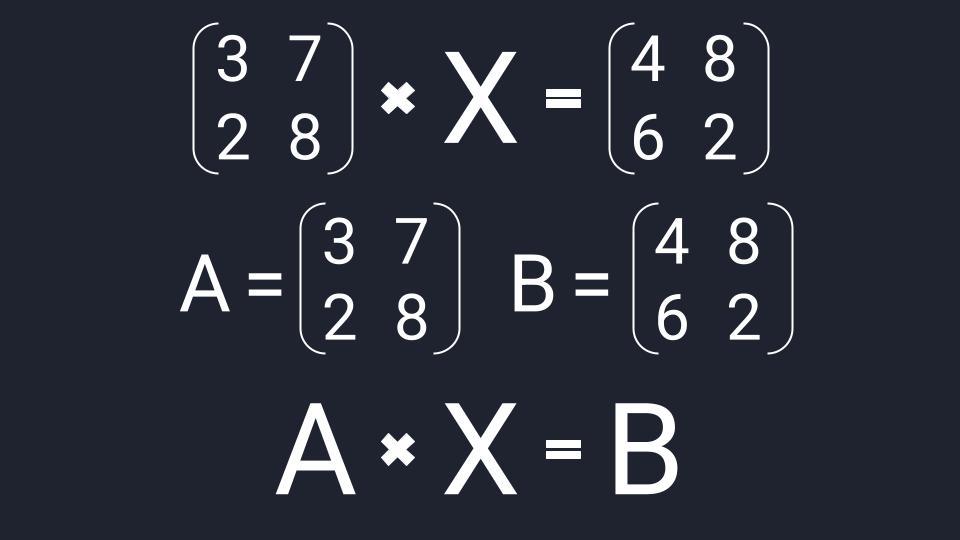
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Шаг 2. Вводим единичную матрицу
В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.
Можно представить, что есть число 100 — это «сто в первой степени», 100 1
И есть число 0,01 — это «сто в минус первой степени», 100 -1
При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.
Вот такое, только в мире матриц.
Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:
А -1 × А × Х = А -1 × В
Добавляем единичную матрицу и упрощаем запись:
А -1 × А = E — единичная матрица
E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем
Х = А -1 × В — новая запись уравнения
После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.
💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.
Видео:Решение системы уравнений методом ГауссаСкачать

Шаг 3. Находим обратную матрицу
Вспоминаем формулу и порядок расчёта обратной матрицы:
- Делим единицу на определитель матрицы A.
- Считаем транспонированную матрицу алгебраических дополнений.
- Перемножаем значения и получаем нужную матрицу.
Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Видео:ТФКП Побережный В.А. Семинар 23.01.24Скачать

Шаг 4. Вычисляем неизвестную матрицу
Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Видео:Решение системы уравнений методом Крамера.Скачать

Шаг 5. Проверяем уравнение
Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.
👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:
Видео:Матричный метод решения систем уравненийСкачать

Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы
В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.
Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.
Найти решение системы n линейных уравнений с n неизвестными:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n
Матричный вид записи: А × X = B
где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.
X = x 1 x 2 ⋮ x n — столбец неизвестных,
B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.
Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1 :
A — 1 × A × X = A — 1 × B .
Так как А — 1 × А = Е , то Е × X = А — 1 × В или X = А — 1 × В .
Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .
В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.
Видео:Обратная матрицаСкачать

Пример решения системы линейных уравнений с помощью метода обратной матрицы
Решаем СЛАУ методом обратной матрицы:
2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2
- Записываем систему в виде матричного уравнения А X = B , где
А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .
- Выражаем из этого уравнения X :
- Находим определитель матрицы А :
d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × ( — 2 ) × 5 + 3 × ( — 4 ) × 4 + 3 × ( — 1 ) × 1 — 3 × ( — 2 ) × 3 — — 1 × ( — 4 ) × 5 — 2 × 4 — ( — 1 ) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25
d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А — 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :
А 11 = ( — 1 ) ( 1 + 1 ) — 2 4 — 1 5 = — 10 + 4 = — 6 ,
А 12 = ( — 1 ) 1 + 2 1 4 3 5 = — ( 5 — 12 ) = 7 ,
А 13 = ( — 1 ) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,
А 21 = ( — 1 ) 2 + 1 — 4 3 — 1 5 = — ( — 20 + 3 ) = 17 ,
А 22 = ( — 1 ) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,
А 23 = ( — 1 ) 2 + 3 2 — 4 3 — 1 = — ( — 2 + 12 ) = — 10 ,
А 31 = ( — 1 ) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,
А 32 = ( — 1 ) 3 + 2 2 3 1 4 = — ( 8 — 3 ) = — 5 ,
А 33 = ( — 1 ) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 .
- Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :
А * = — 6 7 5 17 1 — 10 — 10 — 5 0
- Записываем обратную матрицу согласно формуле:
A — 1 = 1 d e t A ( A * ) T : А — 1 = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 ,
- Умножаем обратную матрицу А — 1 на столбец свободных членов В и получаем решение системы:
X = A — 1 × B = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 1 3 2 = — 1 25 — 6 + 51 — 20 7 + 3 — 10 5 — 30 + 0 = — 1 0 1
Ответ: x 1 = — 1 ; x 2 = 0 ; x 3 = 1
Видео:Решение системы уравнений методом обратной матрицы.Скачать

Решение матриц методы решений и примеров для чайников, формулы вычислений и действий с матрицами
В высшей математике существует понятие матрицы системы чисел. С комбинацией элементов, заключённых в таблице, выполняют различные операции. Прежде чем переходить к решению матриц сложными методами, следует ознакомиться с понятием этого выражения и простейшими логическими операциями над ним.
Видео:МАТРИЦЫ математика УМНОЖЕНИЕ МАТРИЦ и простейшие операции с матрицамиСкачать

Понятие выражения
Определение гласит, что матрица — это прямоугольная таблица с заключёнными в ней числами. Её название обозначается латинскими прописными буквами (А, В). Таблицы бывают разной размерности — прямоугольной, квадратной, а также в виде строк и столбцов.
От количества строк и столбцов будет зависеть величина таблицы. Матрица размера m*n означает, что в таблице содержится m строк и n столбцов. Допустим, первая строка включает элементы а11, а12, а13, вторая — а21, а22, а23. Тогда элементы, где i = j (а11, а22) образовывают диагональ и называются диагональными.
Различают комплексные матрицы, у которых хотя бы один элемент равен комплексному числу, и действительные, когда все её элементы являются действительными числами. В математике комплексные числа представлены в виде a+b*i, где:
- a — действительная часть числа;
- b — мнимая часть;
- i — мнимая единица (квадратный корень из -1).
На приведенном примере показаны варианты.
Простейшие действия с матрицами могут быть разными. К их числу относятся:
- умножение;
- вычитание;
- умножение на число;
- перемножение между собой;
- транспортирование матриц.
Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Сложение и вычитание
Действия по сложению возможны только тогда, когда матрицы одинакового порядка равны между собой. В итоге получится новое матричное выражение такой же размерности. Сложение и вычитание выполняются по общей схеме — над соответствующими элементами таблиц проводят необходимые операции. Например, нужно сложить две матрицы А и В размерности 2*2.
Каждый элемент первой строки складывается по порядку с показателями верхней строчки второй матрицы. По аналогии производится вычитание, только вместо плюса ставится минус.
Видео:Матрицы: начало. Высшая математикаСкачать

Умножение на число
Любую таблицу чисел можно умножить на число. Тогда каждый её элемент перемножается с этим показателем. К примеру, умножим матричное выражение на 2:
Видео:§28 Матричные уравненияСкачать

Операция перемножения
Матрицы подлежат перемножению одна на другую, когда количество столбцов первой таблицы равно числу строк второй. Каждый элемент Aij будет равняться сумме произведений элементов i-строки первой таблицы, перемноженных на числа в j-столбце второй. Способ произведения наглядно представлен на примере.
Видео:Как найти определитель матрицы 2х2, 3х3 и 4х4Скачать

Возведение в степень
Формулу возведения в степень применяют только для квадратных матричных выражений. При этом степень должна быть натуральной. Формула возведения следующая:
Иначе, чтобы выполнить операцию возведения таблицы чисел в степень n, требуется умножить её на себя саму n раз. Для операции возведения в степень удобно применять свойство в соответствии с формулой:
Решение представлено на примере. 1 этап: необходимо возвести в степень, где n = 2.
2 этап: сначала возводят в степень n =2. Согласно формуле перемножают таблицу чисел саму на себя n = 2 раз.
3 этап: в итоге получаем:
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Расчёт определителя
В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.
Определителем матрицы А n-энного порядка называется число, которое получают из алгебраической суммы n! слагаемых, попадающих под определённые критерии. Эти слагаемые являются произведением n-элементов, взятых единично из всех столбов и строк.
Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:
Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:
Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:
Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.
Видео:Решение системы трех уравнений по формулам КрамераСкачать

Обратная матрица
Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами. На рисунке представлен метод решения:
По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.
Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.
Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:
Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2. На первом этапе выполняют действия:
Обратного выражения матрицы не может быть, если определитель равен нулю. В рассматриваемом случае он равен -2, поэтому всё в порядке.
2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках.
При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:
3 этап: находят алгебраические дополнения.
4 этап: определяют транспонированную матрицу.
Проверка решения: чтобы удостовериться, что обратная таблица чисел найдена верно, следует выполнить проверочную операцию.
В рассматриваемом примере получается единичная матрица, когда на главной диагонали находятся единицы, при этом другие элементы равняются нулю. Это говорит о том, что решение было найдено правильно.
Видео:Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Нахождение собственных векторов
Определение собственного вектора и значений матричного выражения легче понять на примере. Для этого задают матричную таблицу чисел и ненулевой вектор Х, называемый собственным для А. Пример выражения:
Согласно теореме собственными числами матричного выражения будут корни характеристического уравнения:
Из однородной системы уравнений можно определить координаты собственного вектора Х, который соответствует значению лямбда.
Видео:Решение системы уравнений методом Крамера 2x2Скачать

Метод Гаусса
Методом Гаусса называют способ преобразования системы уравнений линейного вида к упрощённой форме для дальнейшего облегчённого решения. Операции упрощения уравнений выполняют с помощью эквивалентных преобразований. К таким относят:
- действия, когда в системе переставляются местами два уравнения;
- произведение одного из уравнений в системе на действительное ненулевое число;
- сложение первого уравнения со вторым, при этом последнее умножено на произвольное число.
Чтобы понять механизм решения, следует рассмотреть линейную систему уравнений.
Следует переписать эту систему в матричный вид:
А будет являться таблицей коэффициентов системы, b — это правая часть ограничений, а Х — вектор переменных координат, который требуется найти. Для решения используют ранг матрицы. Под ним понимают наивысший порядок минора, который отличается от 0.
В этом примере rang (A) = p. Способ эквивалентных преобразований не изменяет ранг таблицы коэффициентов.
Метод Гаусса предназначен для приведения матричной таблицы коэффициентов А к ступенчатому или диагональному виду. Расширенная система выглядит так:
Допустим, а11 не равен 0. В противном случае, если это не так, то меняют эту строку с другой, где в первом столбце находится элемент, отличный от нуля. Когда подобные строчки отсутствуют, переходят к другому столбцу. Все нижние элементы столбца после а11 обнуляют. Для этих целей выполняют операции сложения строк 2,3…m с первой строчкой, умноженной на а21/а11, -а31/а11….- аm1/a11. В результате система примет вид:
На втором шаге повторяют все действия с элементами столбца 2, которые расположены ниже а22. Если показатель равен нулю, строку также меняют местами со строчкой, лежащей ниже с ненулевым элементом во втором столбце. Затем обнулению подлежат все показатели ниже а22. Для этого складывают строки 2,3 ..m, как описано выше. Выполняя процедуру со всеми элементами, приходят к матричной таблице ступенчатого или диагонального вида. Полученная расширенная таблица будет выглядеть:
Обращают внимание на последние строки.
В этом случае система уравнений имеет решение, но когда хотя бы одно из этих чисел отличается от нуля, она несовместима. Таким образом, система совместима, если ранг таблицы А равен расширенному рангу В (А|b).
Если rang А=rang (A|b), то существует множество решений, где n-p — многообразие. Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.
Найти быстро ответ и проверить себя позволяет онлайн-калькулятор. Решение матрицы методом Гаусса с помощью такого расчёта показывает подробные этапы операций. Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».
Способ Крамера
Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:
Её необходимо заменить равноценным матричным уравнением.
Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:
В итоге получают выражения:
Из представленных уравнений выделяют формулы Крамера:
Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:
Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.
Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.