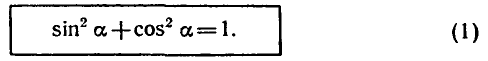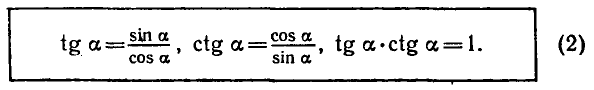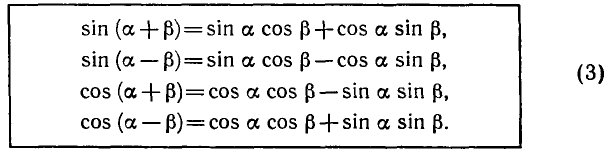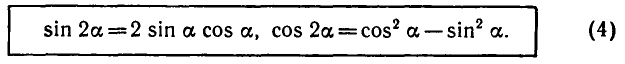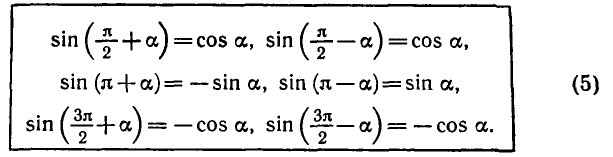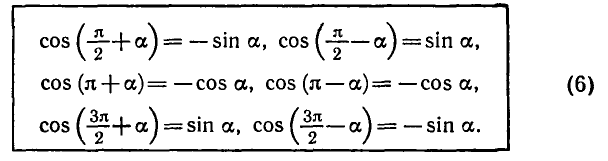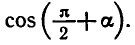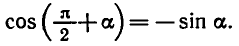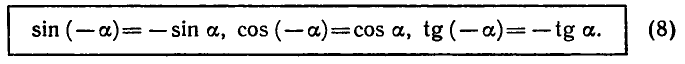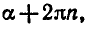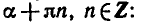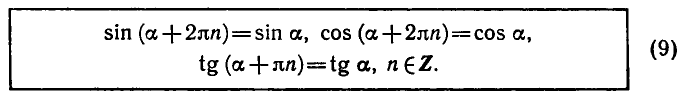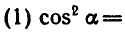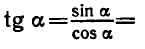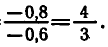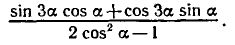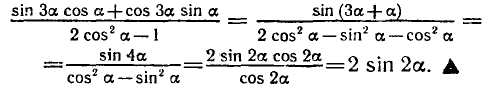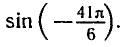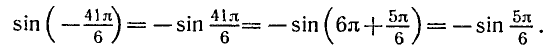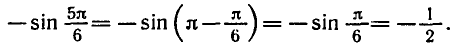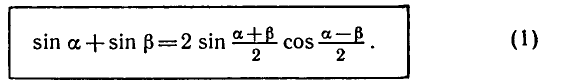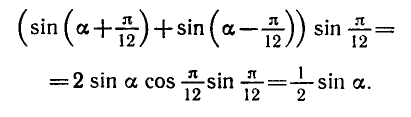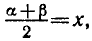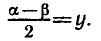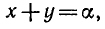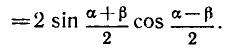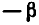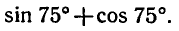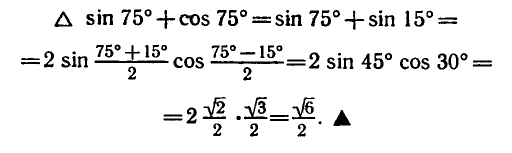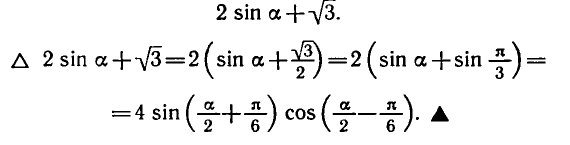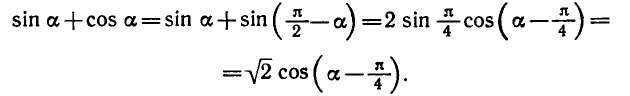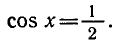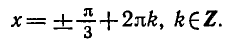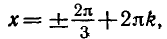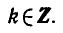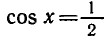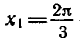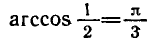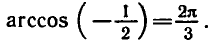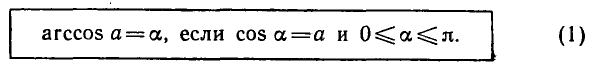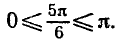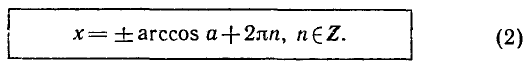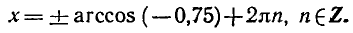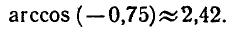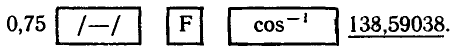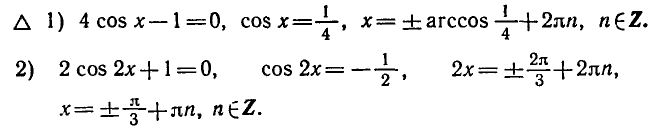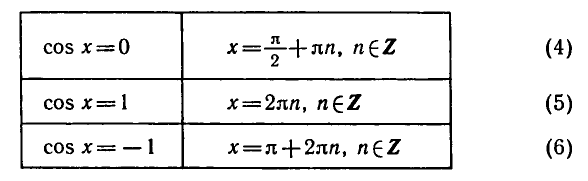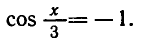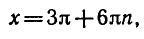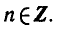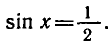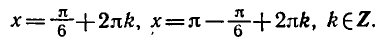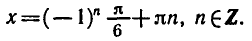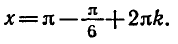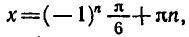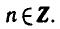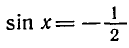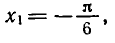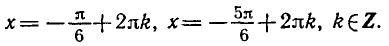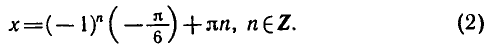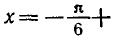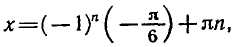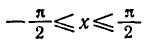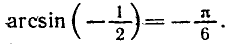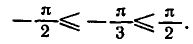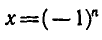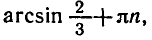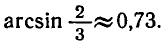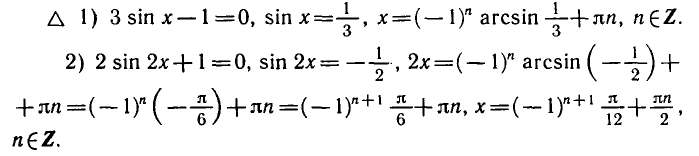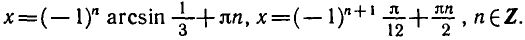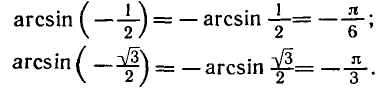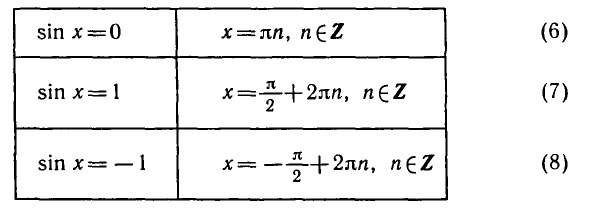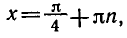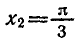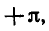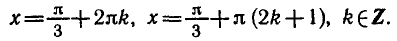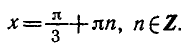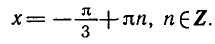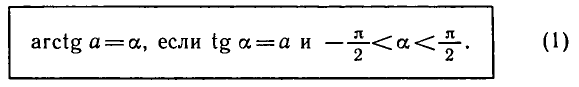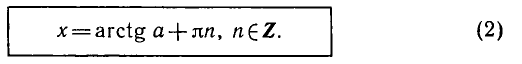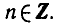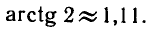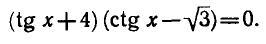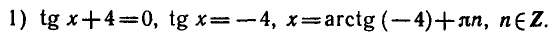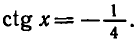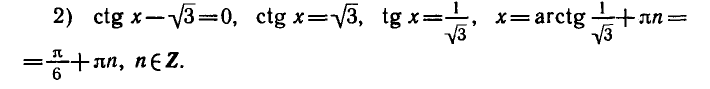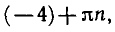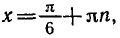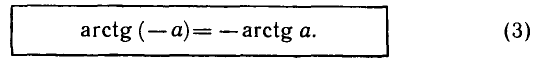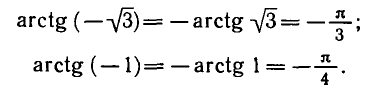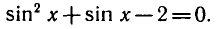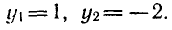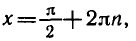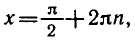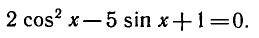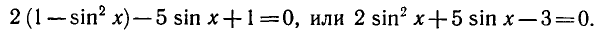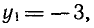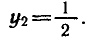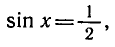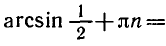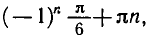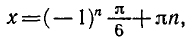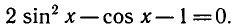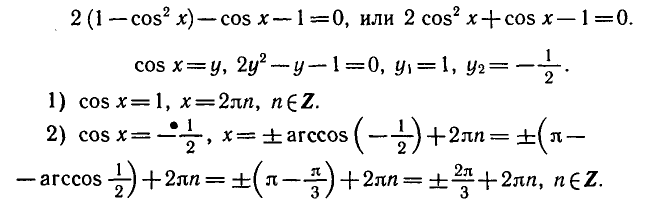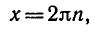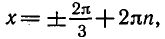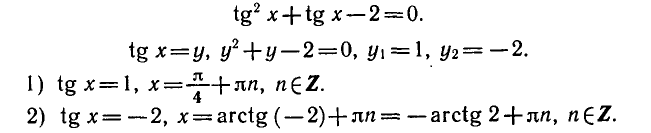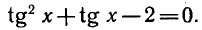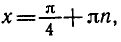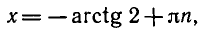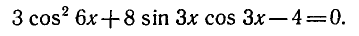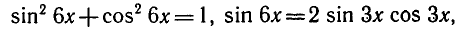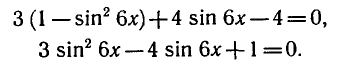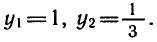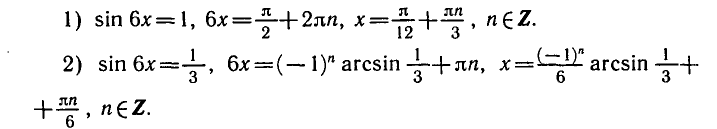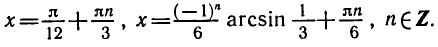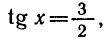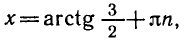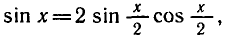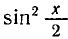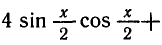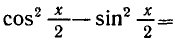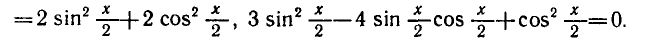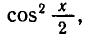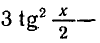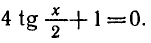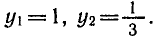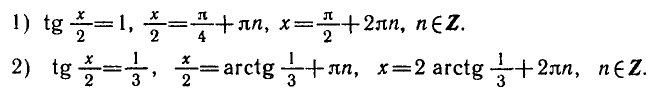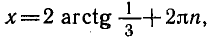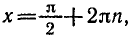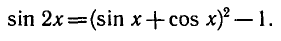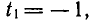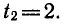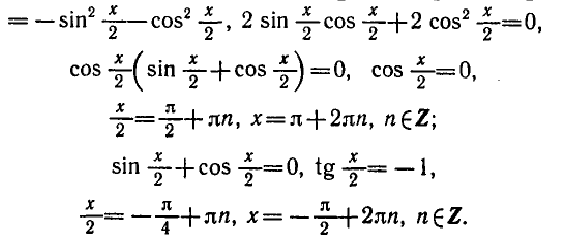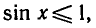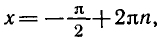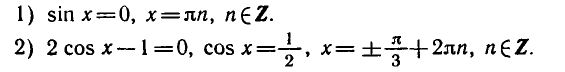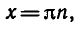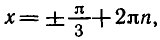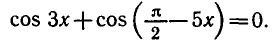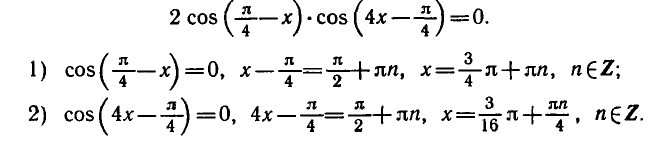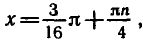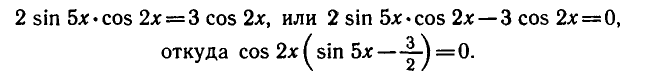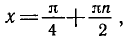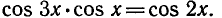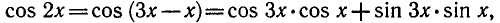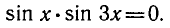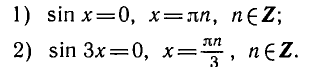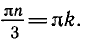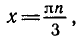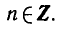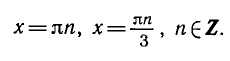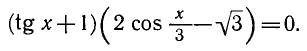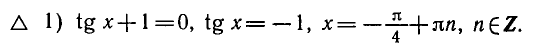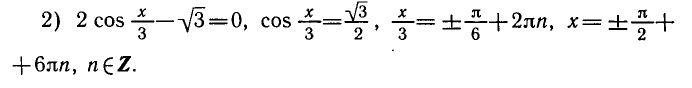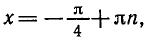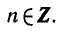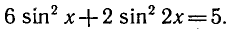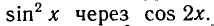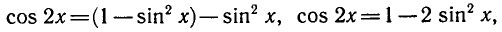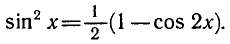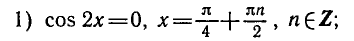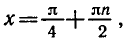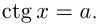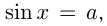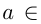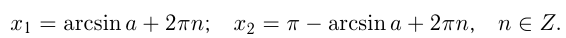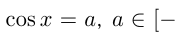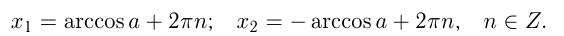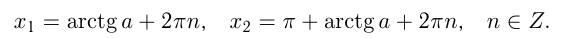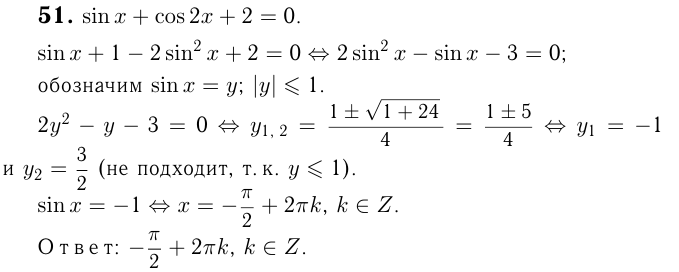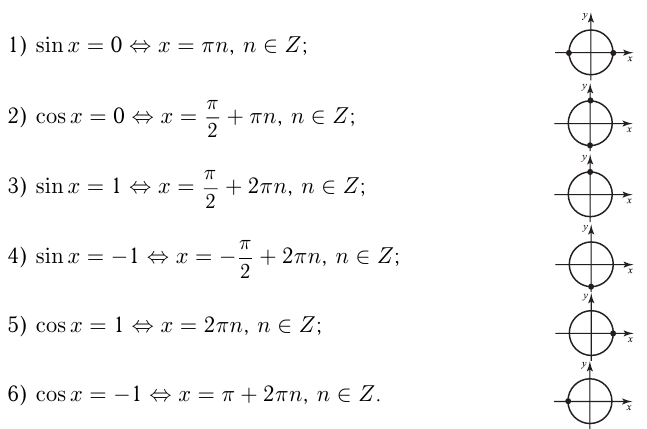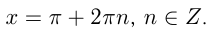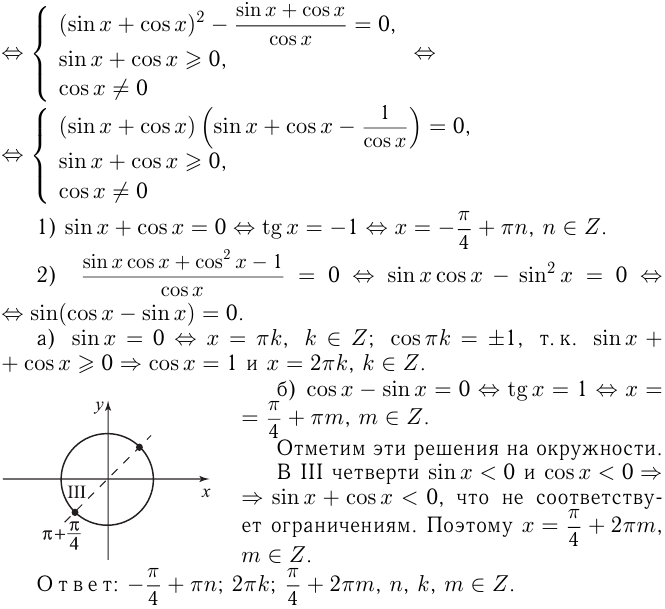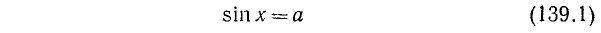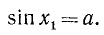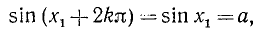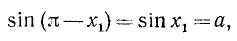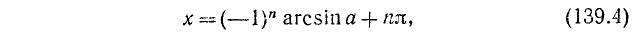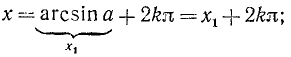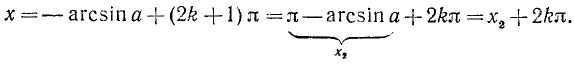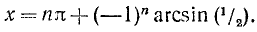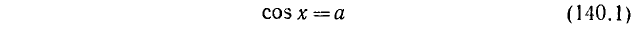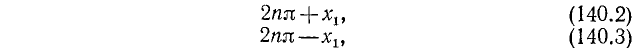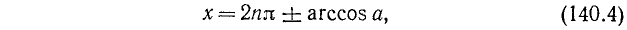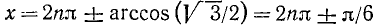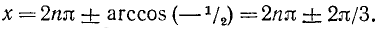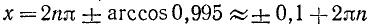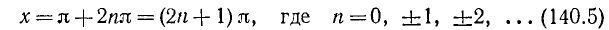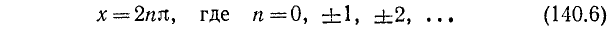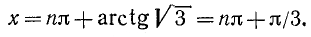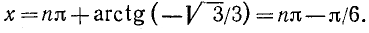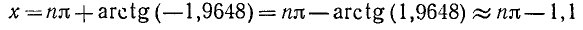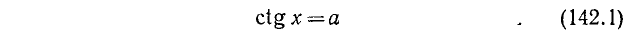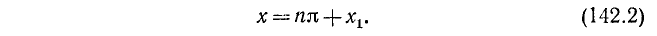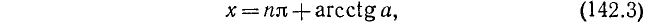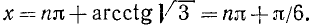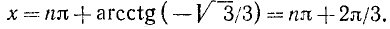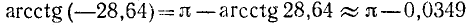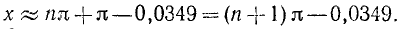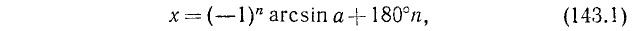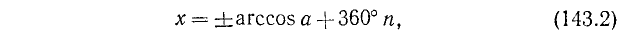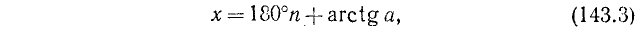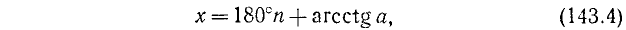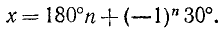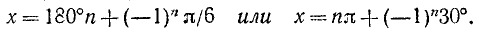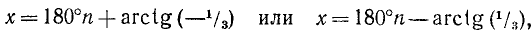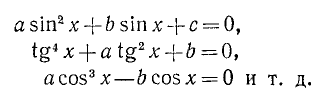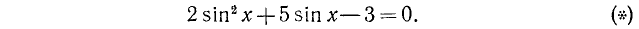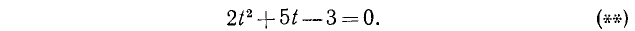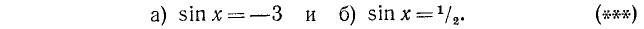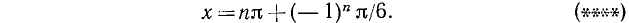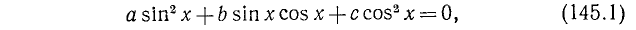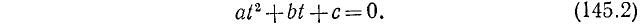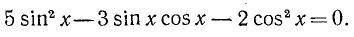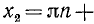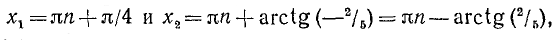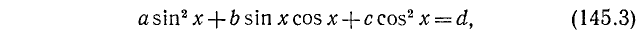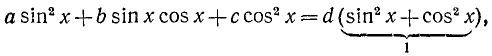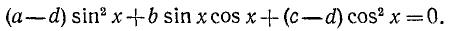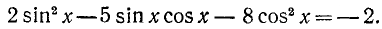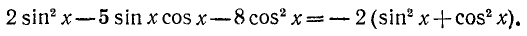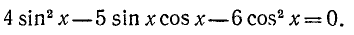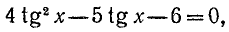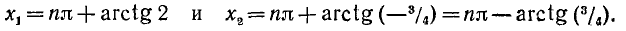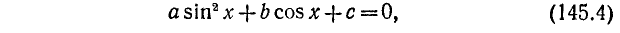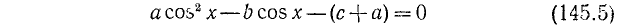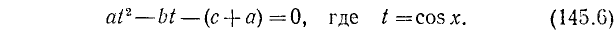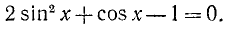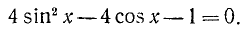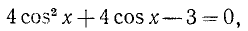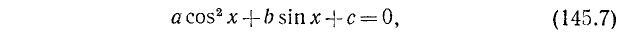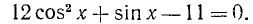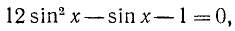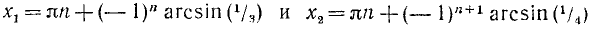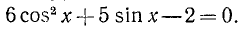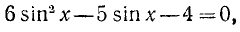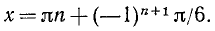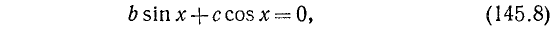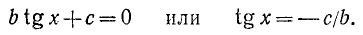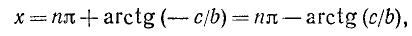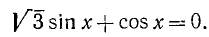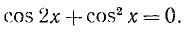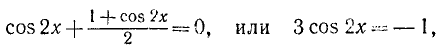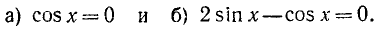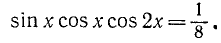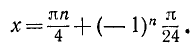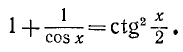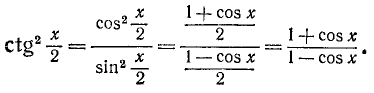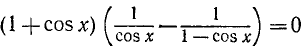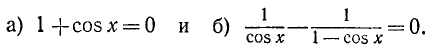РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Простейшими тригонометрическими уравнениями называют уравнения
Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.
19.1. Уравнение cos x = a
Объяснение и обоснование
- Корни уравненияcosx=a.
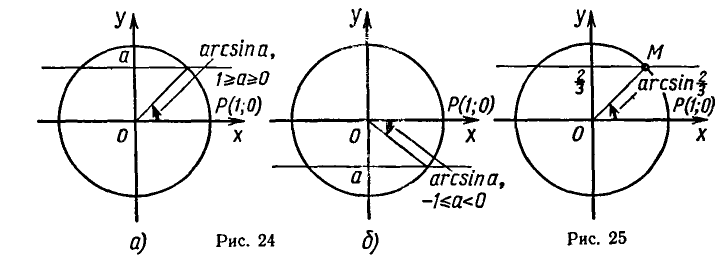
При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a n arcsin a + 2πn, n ∈ Z (3)
2.Частые случаи решения уравнения sin x = a.
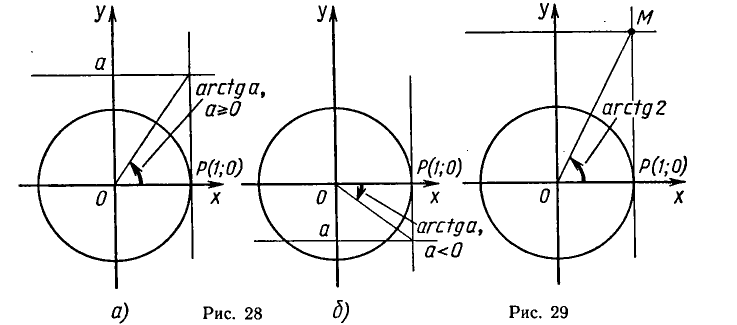
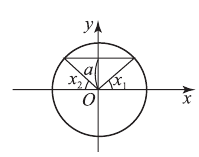
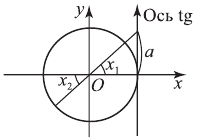
Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).
Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда
Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,
Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,
Примеры решения задач
Замечание. Ответ к задаче 1 часто записывают в виде:
19.3. Уравнения tg x = a и ctg x = a
Объяснение и обоснование
1.Корни уравнений tg x = a и ctg x = a
Рассмотрим уравнение tg x = a. На промежутке 
Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:
При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).
Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a.
Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:
таким образом, уравнение ctg x = 0 имеет корни
Примеры решения задач
Вопросы для контроля
- Какие уравнения называют простейшими тригонометрическими?
- Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
- Выведите формулы решения простейших тригонометрических уравнений.
- Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.
Упражнения
Решите уравнение (1-11)
Найдите корни уравнения на заданном промежутке (12-13)
- Простейшие тригонометрические уравнения. Часть 1
- Уравнения и
- Линия тангенсов.
- Уравнение
- Тригонометрические уравнения и неравенства с примерами решения и образцами выполнения
- Тригонометрические формулы
- Сумма и разность синусов. Сумма и разность косинусов
- Уравнение cos х = а
- Уравнение sin х= а
- Уравнение tg x = а
- Решение тригонометрических уравнений
- Уравнения, сводящиеся к квадратам
- Уравнения вида a sin х + b cos х = с
- Уравнения, решаемые разложением левой части на множители
- Тригонометрические уравнения и неравенства — основные понятия и определения
- Уравнения, разрешенные относительно одной из тригонометрических функций
- Уравнение sin х = а
- Уравнение cos x = a
- Уравнение tg x = a
- Уравнение ctg х = а
- Некоторые дополнения
- Способ приведения к одной функции одного и того же аргумента
- Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента
- Способ разложения на множители
- 📹 Видео
Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Простейшие тригонометрические уравнения. Часть 1
Простейшими называются тригонометрические уравнения следующих четырёх видов:
Любое тригонометрическое уравнение в конечном счёте сводится к решению одного или нескольких простейших. К сожалению, на этом заключительном стандартном шаге школьники часто допускают ошибки, что ведет к потере баллов на ЕГЭ. Именно поэтому так важна данная тема.
Существуют два подхода к решению простейших тригонометрических уравнений.
Первый подход — бессмысленный и тяжёлый. Следуя ему, надо выучить по шпаргалке общие формулы, а также все частные случаи. Польза от этого столь же невелика, как от зубрежки шестнадцати строк заклинаний на непонятном языке. Мы отказываемся от такого подхода раз и навсегда.
Второй подход — логический и наглядный. Для решения простейших тригонометрических уравнений мы пользуемся тригонометрическим кругом и определениями тригонометрических функций.
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Уравнения и
Напомним, что — абсцисса точки на единичной окружности, соответствующей углу , а — её ордината.
Из определения синуса и косинуса следует, что уравнения и имеют решения только при условии .
Абитуриент, будь внимателен! Уравнения или решений не имеют!
Начнём с самых простых уравнений.
. .
Мы видим, что на единичной окружности имеется лишь одна точка с абсциссой 1:

Эта точка соответствует бесконечному множеству углов: . Все они получаются из нулевого угла прибавлением целого числа полных углов (т. е. нескольких полных оборотов как в одну, так и в другую сторону).
Следовательно, все эти углы могут быть записаны одной формулой:
Это и есть множество решений данного уравнения. Напоминаем, что — это множество целых чисел.
Снова видим, что на единичной окружности есть лишь одна точка с абсциссой :
Эта точка соответствует углу и всем углам, отличающихся от на несколько полных оборотов в обе стороны, т. е. на целое число полных углов. Следовательно, все решения данного уравнения записываются формулой:
. .
Отмечаем на тригонометрическом круге единственную точку с ординатой :
И записываем ответ:
Обсуждать тут уже нечего, не так ли? 🙂
Можете, кстати, записать ответ и в другом виде:
Это — дело исключительно вашего вкуса.
Заодно сделаем первое полезное наблюдение. Чтобы описать множество углов, отвечающих одной-единственной точке тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .
На тригонометрическом круге имеются две точки с ординатой 0:
Эти точки соответствуют углам Все эти углы получаются из нулевого угла прибавлением целого числа углов (т. е. с помощью нескольких полуоборотов в обе стороны). Таким образом,
Точки, лежащие на концах диаметра тригонометрического круга, мы будем называть диаметральной парой.
Точки с абсциссой 0 также образуют диаметральную пару, на сей раз вертикальную:
Все углы, отвечающие этим точкам, получаются из — прибавлением целого числа углов (полуоборотов):
Теперь мы можем сделать и второе полезное наблюдение.
Чтобы описать множество углов, отвечающих диаметральной паре точек тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .
Переходим к следующему этапу. Теперь в правой части будет стоять табличное значение синуса или косинуса (отличное от 0 или ). Начинаем с косинуса.
Имеем вертикальную пару точек с абсциссой :
Все углы, соответствующие верхней точке, описываются формулой (вспомните первое полезное наблюдение!):
Аналогично, все углы, соответствующие нижней точке, описываются формулой:
Обе серии решений можно описать одной формулой:
Остальные уравнения с косинусом решаются совершенно аналогично. Мы приводим лишь рисунок и ответ.
Теперь рассмотрим уравнения с синусом. Тут ситуация немного сложнее.
Имеем горизонтальную пару точек с ординатой :
Углы, отвечающие правой точке:
Углы, отвечающие левой точке:
Описывать эти две серии одной формулой никто не заставляет. Можно записать ответ в таком виде:
Тем не менее, объединяющая формула существует, и её надо знать. Выглядит она так:
На первый взгляд совершенно не ясно, каким образом она дает обе серии решений. Но давайте посмотрим, что получается при чётных . Если , то
Мы получили первую серию решений . А если — нечетно, , то
Это вторая серия .
Обратим внимание, что в качестве множителя при обычно ставится правая точка, в данном случае .
Остальные уравнения с синусом решаются точно так же. Мы приводим рисунок, запись ответа в виде совокупности двух серий и объединяющую формулу.
На этом с синусом и косинусом пока всё. Переходим к тангенсу.
Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Линия тангенсов.
Начнём с геометрической интерпретации тангенса — так называемой линии тангенсов. Это касательная к единичной окружности, параллельная оси ординат (см. рисунок).
Из подобия треугольников и имеем:
Мы рассмотрели случай, когда находится в первой четверти. Аналогично рассматриваются случаи, когда находится в остальных четвертях. В результате мы приходим к следующей геометрической интерпретации тангенса.
Тангенс угла равен ординате точки , которая является точкой пересечения линии тангенсов и прямой , соединяющей точку с началом координат.
Вот рисунок в случае, когда находится во второй четверти. Тангенс угла отрицателен.
Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Уравнение
Заметим, что тангенс может принимать любые действительные значения. Иными словами, уравнение имеет решения при любом .
.
Имеем диаметральную горизонтальную пару точек:

Эта пара, как мы уже знаем, описывается формулой:
Имеем диаметральную пару:
Вспоминаем второе полезное наблюдение и пишем ответ:
Остальные уравнения с тангенсом решаются аналогично. Мы приводим лишь рисунки и ответы.
На этом заканчиваем пока и с тангенсом.
Уравнение нет смысла рассматривать особо. Дело в том, что:
уравнение равносильно уравнению ;
при уравнение равносильно уравнению .
Впрочем, существует также и линия котангенсов, но. . . Об этом мы вам расскажем на занятиях 🙂
Итак, мы разобрали простейшие тригонометрические уравнения, содержащие в правой части табличные значения тригонометрических функций. Именно такие задачи встречаются в части В вариантов ЕГЭ.
А что делать, например, с уравнением ? Для этого надо сначала познакомиться с обратными тригонометрическими функциями. О них мы расскажем вам в следующей статье.
Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Тригонометрические уравнения и неравенства с примерами решения и образцами выполнения
Корень уравнения есть число, которое, будучи подставленным в
уравнение вместо обозначающей его буквы или вида, приводит к
исчезновению всех его членов.
И. Ньютон
Видео:СИНУС КОСИНУС ТАНГЕНС угла 10 класс РЕШЕНИЕ ПРИМЕРОВСкачать

Тригонометрические формулы
В курсе алгебры рассматривались синус, косинус и тангенс
произвольного угла, выраженного в градусах или радианах.
Там же были доказаны основные формулы, которые
использовались для преобразований тригонометрических выражений.
Напомним эти формулы:
1. Основное тригонометрическое тождество:
2. Зависимость между синусом, косинусом, тангенсом и котангенсом:
Ньютон Исаак (1643— 1727) — английский математик, физик, механик, астроном; основоположник современной механики; одновременно с немецким математиком Г. Лейбницем ему принадлежит разработка дифференциального и интегрального исчислений.
3. Формулы сложения:
4. Формулы синуса и косинуса двойного угла:
5. Формулы приведения:
Формулы приведения запоминать необязательно. Для того
чтобы записать любую из них, можно руководствоваться
следующими правилами:
1) В правой части формулы который
2) Если в левой части формулы угол равен 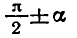
то синус заменяется на косинус, тангенс —
на котангенс и наоборот. Если угол равен 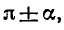
не происходит.
Например, покажем, как с помощью этих правил можно
получить формулу приведения для
По первому правилу в правой части формулы нужно поставить знак >,
так как если 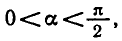
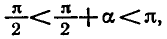
6. Формулы синуса, косинуса, тангенс угла
7. Формулы синуса и косинуса угла
тангенса угла
Приведем несколько примеров применения формул (1) — (9).
Пример:
Вычислить 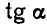
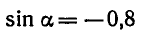
Сначала найдем 
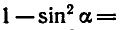
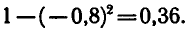
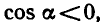
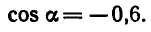
Пример:
Используя формулы (1), (3) и (4), получаем:
Пример:
Вычислить
Используя формулы (8) и (9), получаем:
По формулам приведения находим:
Ответ.
Сумма и разность синусов. Сумма и разность косинусов
Пример:
Используя формулу сложения и формулу синуса двойного
угла, получаем:
Эту задачу можно решить проще, если использовать формулу
суммы синусов:
С помощью этой формулы получаем:
Докажем теперь справедливость формулы (1).
Обозначим
Тогда 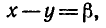
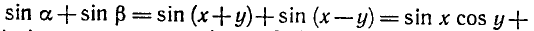
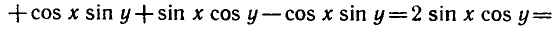
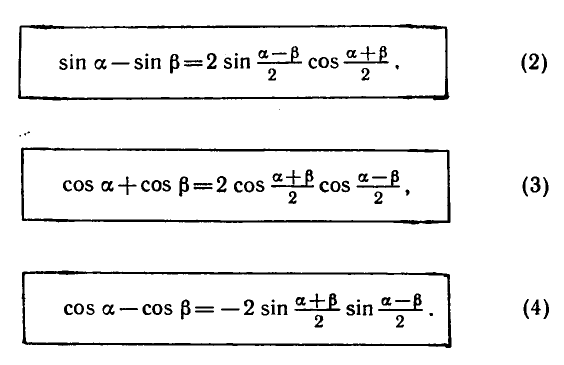
Наряду с формулой (1) используются формула разности
синусов, а также формулы суммы и разности косинусов:
Формулы (3) и (4) доказываются так же, как и формула (1);
формула (2 ) получается из формулы ( 1 ) заменой 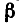
(докажите самостоятельно).
Пример:
Вычислить
Пример:
Преобразовать в произведение
Пример:
Доказать, что наименьшее значение выражения 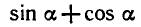
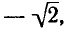
Преобразуем данное выражение в произведение:
Так как наименьшее значение косинуса равно — 1, а наибольшее равно 1, то наименьшее значение данного выражения
равно 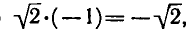
Уравнение cos х = а
Из курса алгебры известно, что значения косинуса заключены
в промежутке [— 1; 1], т. е.
Поэтому если |а |> 1 , то уравнение cos x = a не имеет корней. Например, уравнение cos x = — 1,5 не имеет корней.
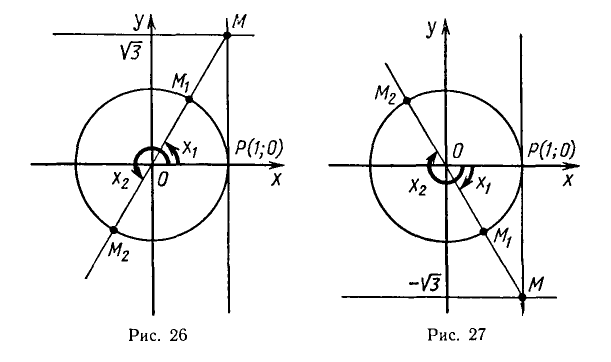
Пример:
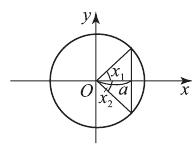
Решить уравнение
Напомним, что cos х — абсцисса точки единичной окружности, полученной поворотом точки Р (1; 0) вокруг начала координат на угол х. Абсциссу, равную имеют две точки окружности
и 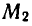
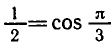
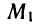
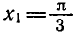
углы 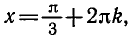
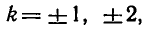
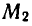
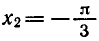
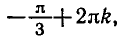
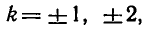
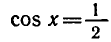
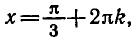
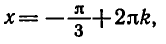
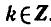
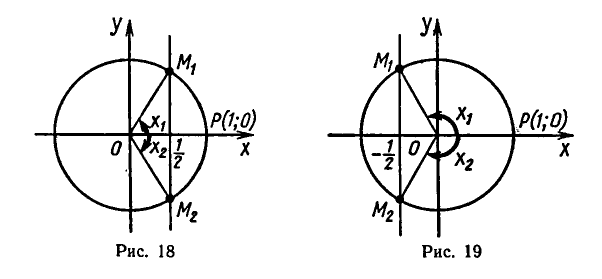
Пример:
Решить уравнение
Абсциссу, равную 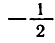
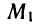
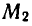
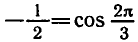
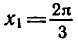
а потому угол 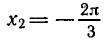
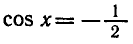
Таким образом, каждое из уравнений
и 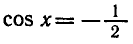
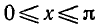
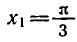
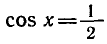
— корень уравнения 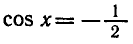
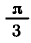
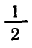
а число 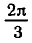
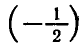
Вообще уравнение 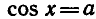

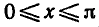
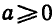
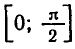
Например, 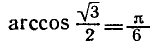
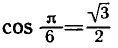
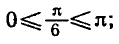
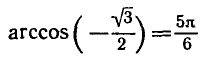
и
Аналогично тому, как это сделано при решении задач 1 и 2, можно показать, что все корни уравнения 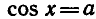
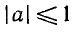
Пример:
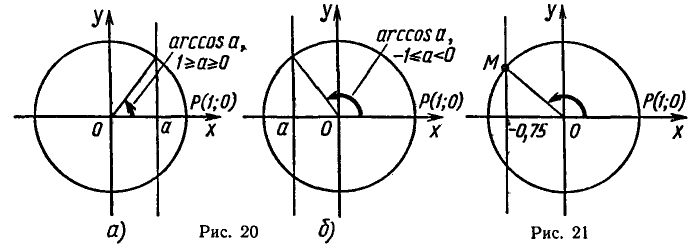
Решить уравнение cos x = — 0,75.
По формуле (2) находим
Значение arccos ( — 0,75) можно приближенно найти на рисунке 21, измеряя угол РОМ транспортиром.
Приближенные значения арккосинуса можно также находить
с помощью специальных таблиц или микрокалькулятора. На
пример, значение arccos (—0,75) можно вычислить на
микрокалькуляторе МК-54 по программе
Итак,
В данном случае переключатель микрокалькулятора Р-ГРД-Г
был установлен в положение Р (радиан).
Если вычисления проводить в градусной мере, то переключатель микрокалькулятора Р-ГРД-Г следует установить в положение Г (градус). Программа вычислений остается прежней:
Итак, 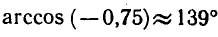
Пример:
Решить уравнение (4 cos х — 1) (2 cos 2x + 1)=0.
Ответ. 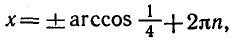
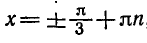
Можно доказать, что для любого 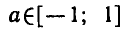
формула
Эта формула позволяет выражать значения арккосинусов
отрицательных чисел через значения арккосинусов
положительных чисел. Например:
Из формулы (2) следует, что корни уравнения cos х = а при а = 0,
а = 1, а = — 1 можно находить по более простым формулам:
Задача 5. Решить уравнение
По формуле (6) получаем 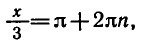
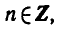
Уравнение sin х= а
Известно, что значения синуса заключены в промежутке
[— 1; 1], т. е. 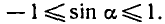
уравнение sin x = a не имеет корней. Например, уравнение
sin x = 2 не имеет корней.
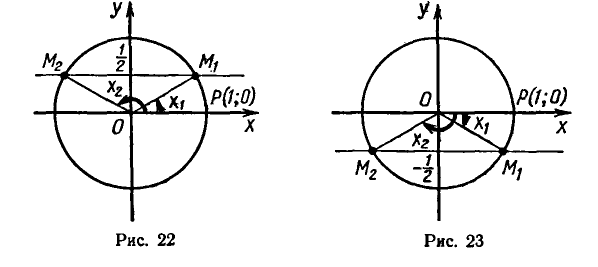
Пример:
Решить уравнение
Напомним, что sin x — ордината точки единичной окружности, полученной поворотом точки Р (1; 0) вокруг начала координат на угол x. Ординату, равную 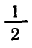
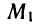
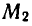
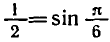
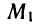
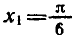
углы 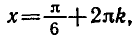
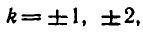
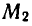
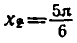
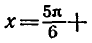
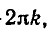
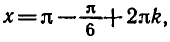
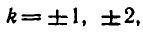
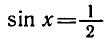
Эти формулы объединяются в одну:
В самом деле, если n — четное число, т. е. n = 2k, то из формулы (1) получаем 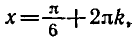
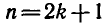
О т в е т .
Пример:
Решить уравнение
Ординату, равную 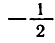
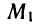
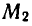
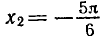
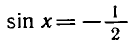
Эти формулы объединяются в одну:
В самом деле, если n = 2k, то по формуле (2) получаем 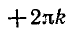
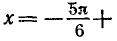
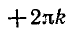
Ответ.
Итак, каждое из уравнений 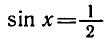
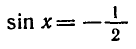
бесконечное множество корней. На отрезке
каждое из этих уравнений имеет только один корень: 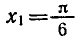
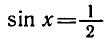
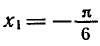
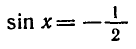
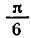
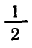
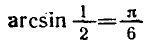
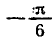
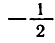
Вообще уравнение sin x = a, где 
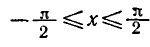
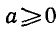
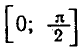
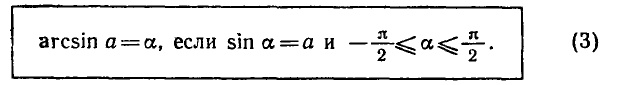
Например, 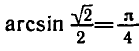
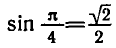
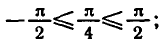
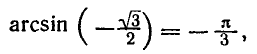
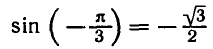
Аналогично тому, как это сделано при решении задач 1 и 2 можно показать, что корни уравнения sin x = a, где 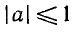
Пример:
Решить уравнение 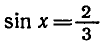
По формуле (4) находим
Значение 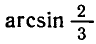
измеряя угол РОМ транспортиром.
Значения арксинуса можно находить с помощью специальных
таблиц или с помощью микрокалькулятора. Например, значение 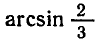
программе
Итак,
При этом переключатель микрокалькулятора Р-ГРД-Г был установлен в положение Р (радиан).
Пример:
Решить уравнение (3 sin х — 1) (2 sin 2х + 1) = 0.
Можно доказать, что для любого 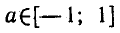
формула
Эта формула позволяет находить значения арксинусов отри
цательных чисел через значения арксинусов положительных
чисел. Например:
Отметим, что из формулы (4) следует, что корни уравнения
sin x = a при а = 0 , а = 1 , а = — 1 можно находить по более
простым формулам:
Пример:
Решить уравнение sin 2х = 1.
По формуле (7) имеем 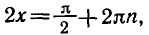
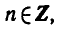
Уравнение tg x = а
Известно, что тангенс может принимать любое действительное
значение. Поэтому уравнение tg x = a имеет корни при любом
значении а.
Пример:
Решить уравнение
Построим углы, тангенсы которых равны 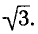
и отложим отрезок 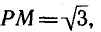
мую. Эта прямая пересекает единичную окружность в двух диа
метрально противоположных точках 
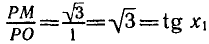
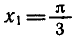
Таким образом, точка 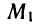
вокруг начала координат на угол а также на углы 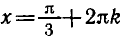
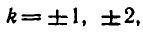
Точка 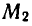
а также на углы 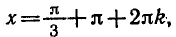
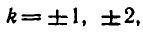
Итак, корни уравнения 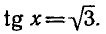
Эти формулы объединяются в одну
Пример:
Решить уравнение
Углы, тангенсы которых равны 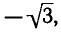
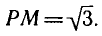
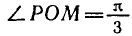

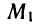
координат на угол 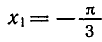
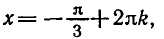
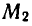
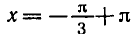
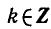
Поэтому корни уравнения 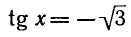
Итак, каждое из уравнений 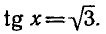
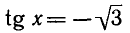
бесконечное множество корней. На интервале — каждое из этих уравнений имеет только один корень: 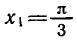
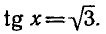
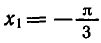
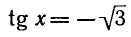
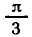
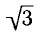
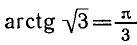
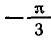
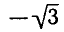
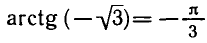
Вообще уравнение tg х = а для любого 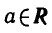
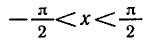
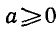
заключен в промежутке 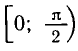
Например, 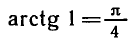
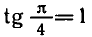
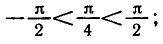
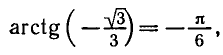
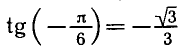
Аналогично тому, как это сделано при решении задач 1 и 2, можно показать, что все корни уравнения tg x = a, где 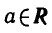
Пример:
Решить уравнение tg х = 2.
По формуле (2) находим
Значение arctg 2 можно приближенно найти из рисунка 29,
измеряя угол РОМ транспортиром.
Приближенные значения арктангенса можно также найти по
таблицам или с помощью микрокалькулятора.
Например, значение arctg 2 можно вычислить на МК-54 по
программе
Итак,
Пример:
При этих значениях х первая скобка левой части исходного
уравнения обращается в нуль, а вторая не теряет смысла, так
как из равенства tg x = — 4 следует, что
Следовательно, найденные значения х являются корнями исходного уравнения.
Эти значения x также являются корнями исходного уравнения, так как при этом вторая скобка левой части уравнения
равна нулю, а первая скобка не теряет смысла.
Ответ. 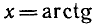
Можно доказать, что для любого 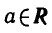
Эта формула позволяет выражать значения арктангенсов
отрицательных чисел через значения арктангенсов положительных чисел.
Например:
Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Решение тригонометрических уравнений
Формулы корней простейших тригонометрических уравнений sin x = a, cos x = a, tg х = а. К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение формул преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратам
Пример:
Решить уравнение
Это уравнение является квадратным относительно sin х.
Обозначив sin x= y, получим уравнение 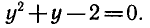
Таким образом, решение исходного уравнения свелось к решению простейших уравнений sin х = 1 и sin х = — 2.
Уравнение sin x = l имеет корни 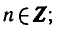
sin x = — 2 не имеет корней.
Ответ.
Пример:
Решить уравнение
Заменяя 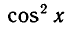
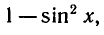
Обозначая sin х = у, получаем 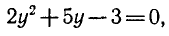
1) sin х = — 3 — уравнение не имеет корней, так как | — 3 | > 1.
2) 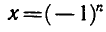
Ответ.
Пример:
Решить уравнение
Используя формулу 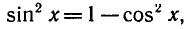
Ответ.
Пример:
Решить уравнение tg x — 2 ctg x + 1 = 0 .
Так как 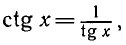
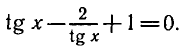
Умножая обе части уравнения на tg x, получаем:
Отметим, что левая часть исходного уравнения имеет смысл,
если 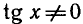
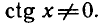
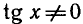
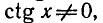
Ответ.
Пример:
Обозначив sin 6 x = у, получим уравнение 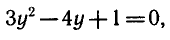
Уравнения вида a sin х + b cos х = с
Пример:
Решить уравнение 2 sin x —3 cos x = 0.
Поделив уравнение на cos x, получим 2tg x — 3 = 0,
При решении этой задачи обе части уравнения 2 sin x — cos x = 0 были поделены на cos x. Напомним, что при делении
уравнения на выражение, содержащее неизвестное, могут быть
потеряны корни. Поэтому нужно проверить, не являются ли
корни уравнения cos x = 0 корнями данного уравнения. Если
cos x = 0, то из уравнения 2 sin x — cos x = 0 следует, что sin x = 0. Однако sin х и cos х не могут одновременно равняться нулю, так как они связаны равенством 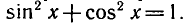
делении уравнения a sin х + b cos x = 0, где 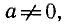
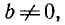
(или sin x) корни этого уравнения не теряются.
Пример:
Решить уравнение 2 sin x + cos x = 2.
Используя формулы 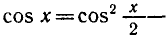
и записывая правую часть уравнения в виде 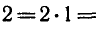
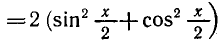
Поделив это уравнение на
Обозначая 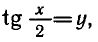
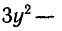
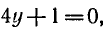
Ответ.
Пример:
Решить уравнение sin 2x — sin x — cos x — 1 = 0.
Выразим sin 2 x через sin x + cos x , используя тождество
Обозначим sin x + cos x = t, тогда 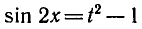
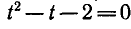
2) Уравнение sin x + cos x = 2 не имеет корней, так как
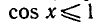
выполняться.
Ответ. 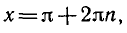
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на
множители.
Пример:
Решить уравнение sin 2х — sin х = 0.
Используя формулу для синуса двойного аргумента, запишем уравнение в виде 2 sin х cos х — sin х = 0.
Вынося общий множитель sin х за скобки, получаем
sin x (2 cos x — 1) = 0
Ответ.
Пример:
Решить уравнение cos Зх + sin 5x = 0.
Используя формулу приведения 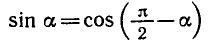
Используя формулу для суммы косинусов, получаем:
Ответ. 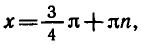
Пример:
Решить уравнение sin 7 x + sin 3 х = 3 cos 2х.
Применяя формулу для суммы синусов, запишем уравнение в виде
Уравнение cos2x = 0 имеет корни 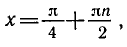
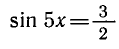
Ответ.
Пример:
Решить уравнение
уравнение примет вид:
Заметим, что числа вида содержатся среди чисел вида 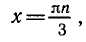
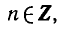
Следовательно, первая серия корней содержится во второй.
Ответ.
Часто бывает трудно усмотреть, что две серии корней, полу
ченных при решении тригонометрического уравнения, имеют об
щую часть. В этих случаях ответ можно оставлять в виде двух
серий. Например, ответ к задаче 12 можно было записать и так:
Пример:
Эти значения х являются корнями исходного уравнения, так
как при этом первая скобка левой части уравнения равна нулю,
а вторая не теряет смысла.
При этих значениях х вторая скобка левой части исходного
уравнения равна нулю, а первая скобка не имеет смысла. Поэтому
эти значения не являются корнями исходного уравнения.
Ответ.
Пример:
Решить уравнение
Выразим
Так как 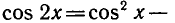
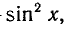
откуда
Поэтому исходное уравнение можно записать так:
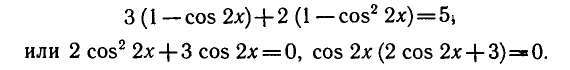
2) уравнение 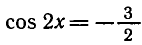
Ответ.
Решение тригонометрического уравнения состоит из двух частей: 1) преобразование тригонометрического выражения к простейшему виду; 2) решение простейшего тригонометрического уравнения. Первая часть сложна из-за множества применяемых формул как тригонометрических, так и алгебраических. Применяются такие приемы как разложение на множители, преобразование суммы или разности тригонометрических функций в произведение и, наоборот, произведения в сумму. Достаточно часто тригонометрические уравнения сводятся к линейным и квадратным уравнениям и уравнениям с корнями. Тригонометрические уравнения во всяком случае имеют ограничения, содержащиеся в тангенсе и котангенсе, т.к. 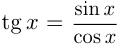
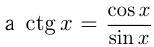
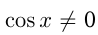
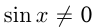
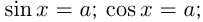
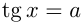
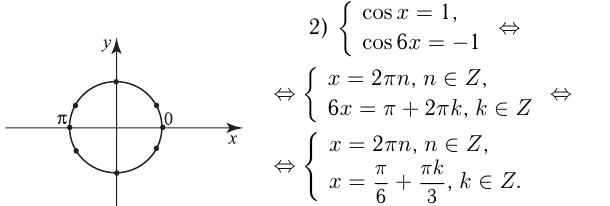
1) Решение уравнения 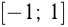
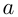
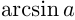
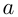
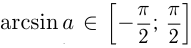
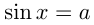
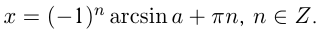
Напоминаем, что ось 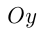
отмечается на оси 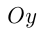
2) Решение уравнения 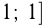
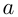
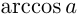
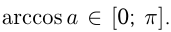
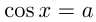
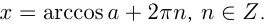
Эти решения отмечены на окружности.
Напоминаем, что ось 
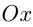
3) Решение уравнения 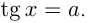
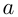
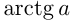
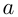
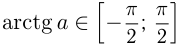
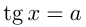
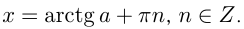
Напоминаем, что значение тангенса отмечается на оси тангенсов, которая параллельна оси 
Там, где возможно, 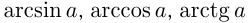
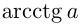
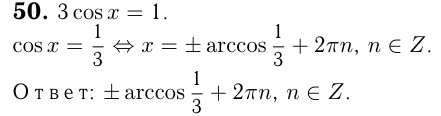
Здесь использована специальная формула, отличная от стандартной для уравнения
Существуют следующие специальные формулы:
Следует заметить также, что буква для обозначения целого числа может быть выбрана любая, но принято брать 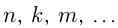
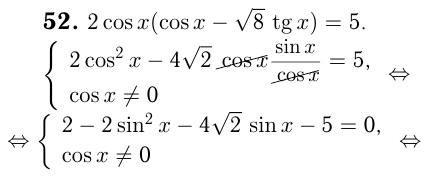
Т.к. решения 1-го и 2-го уравнений должны совпадать, то, как видно на окружности, единственно возможная точка соответствует решению
Эта система, как видно на окружности, решений не имеет
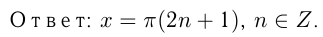

Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Тригонометрические уравнения и неравенства — основные понятия и определения
В этой главе мы рассмотрим некоторые уравнения, а также простейшие системы уравнений, содержащие неизвестную иод знаком тригонометрических функций. Такие уравнения называются тригонометрическими уравнениями.
Приведем некоторые примеры тригонометрических уравнений и их систем:
1) 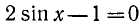
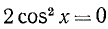
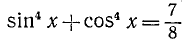
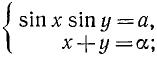
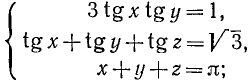
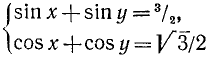
Решение различных типов тригонометрических уравнений большей частью основано на сведении их к некоторым простейшим уравнениям, которые мы рассмотрим ниже. При этом остаются в силе общие правила, относящиеся к решению уравнений. В частности, данное уравнение не всегда приводится к простейшей форме с помощью одних лишь равносильных преобразований. Поэтому следует проверить найденные решения, подставляя их в исходное уравнение.
Тригонометрические уравнения слишком разнообразны для того, чтобы пытаться дать их общую классификацию или общий метод решения. Мы можем указать лишь способы решения некоторых типов таких уравнений.
Уравнения, разрешенные относительно одной из тригонометрических функций
При решении различных тригонометрических уравнений мы будем часто приходить к некоторым простейшим уравнениям, решения которых следует запомнить. Приведем эти уравнения. Для того чтобы можно было дать геометрическую иллюстрацию к этим уравнениям, будем считать х углом в радианной мере.
Уравнение sin х = а
имеет решение при 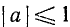
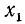
Тогда, в силу периодичности функции sin х, имеем
т.е. и числа вида 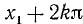
т. е. 
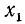
где k= 0, ±1, ±2, …
В качестве 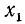
Объединив две серии (139.2) и (139.3) корней данного уравнения sin х = а одной формулой, мы будем записывать в дальнейшем его общее решение (совокупность всех корней) в виде
где n = 0, ±1, ±2, … и 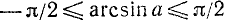
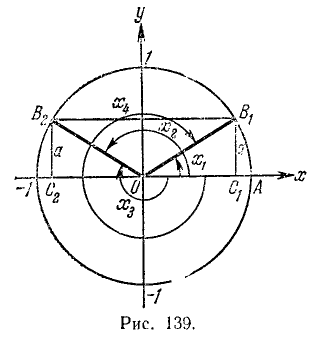
Поясним формулу (139.4) и другим способом, с помощью рис. 139.
Известно, что sin x = а (на рис. 139 ОA = 1, 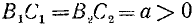
Уравнению (139.1) удовлетворят углы:
а) положительные: 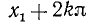
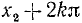
б) отрицательные: 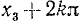
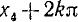
Все эти углы можно задать одной формулой (139.4), и, обратно, любой угол, полученный по формуле (139.4), есть угол либо вида а), либо вида б). Проверим, например, обратное утверждение для положительных углов.
Если 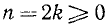
если же 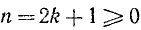
Аналогично проводится проверка и для отрицательных углов.
Пример:
sin x = 1/2.
Решение:
Так как 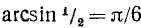
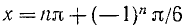
Пример:
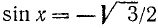
Решение:
Так как 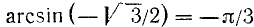
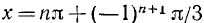
Замечание. При выводе формулы (139.4) мы воспользовались рис. 127, на котором 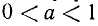
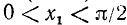
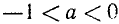
Допустим, что а = 1 или a = — 1. Корни уравнения sin х = 1 можно записать так:
где n = 0, ±1, ±2, …, а корни уравнения sin x = — 1 можно записать так:
где n = 0, ±1, ±2…. . Допустим теперь, что а = 0. Корни уравнения sin x = 0 можно записать так:
Уравнение cos x = a
имеет решение при 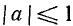
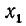
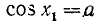
Тогда в силу периодичности 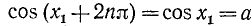
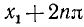

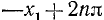
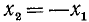
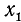
где n = 0, ±1, ±2, …
В качестве 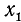
Объединив две серии (140.2) и (140.3) корней уравнения cos x = a одной формулой, мы будем писать в дальнейшем его общее решение (совокупность всех корней) в виде
где n = 0, ±1, ±2, … и 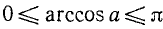
Рекомендуем читателю пояснить формулу (140.4) с помощью рисунка, аналогичного рис. 139.
Пример:
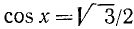
Решение:
Пример:
cos x = — х/2.
Решение:
Пример:
cos х = 0,995.
Решение:
(см. приложение II).
Замечание. При выводе формулы (140.4) мы воспользовались рис. 128, на котором 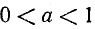
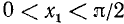
Уравнение cos x = l имеет корни:
Уравнение cos x = 0 имеет корни:
Уравнение tg x = a
имеет решение при любом а (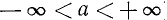
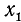
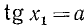
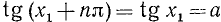
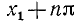
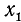
В качестве 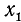
где n = 0, ±1, ±2, … и 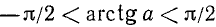
Пример:
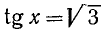
Решение:
Пример:
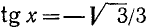
Решение:
Пример:
tg x = —1,9648.
Решение:
(см. приложение II).
Уравнение ctg х = а
имеет решение при любом а (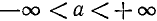
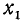
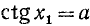
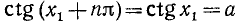
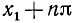
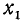
В качестве 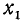
где n = 0, ±1, ±2, … и 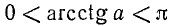
Пример:
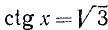
Решение:
Пример:
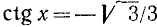
Решение:
Пример:
ctg х = —28,64.
Решение:
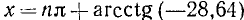
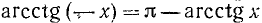
(см. приложение I). Следовательно,
Некоторые дополнения
Если в уравнениях sin x = a, cos х = а, tg х = а и ctg x = a известно, что х — угол в градусной мере, то общие решения нужно записывать по-другому.
Для уравнения sin x = a, где 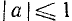
где n = 0, ±1, ±2, … и 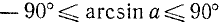
Для уравнения cos х = а, где 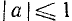
где n = 0, ±1, ±2, … и 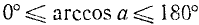
Для уравнения tg х = а, где а — любое число, нужно писать:
где n = 0, ±1, ±2, … и — 90°
где n = 0, ±1, ±2. … и 0°
б) Нельзя, однако, писать
Разберем примеры уравнений, непосредственно сводящихся к уже рассмотренным.
Пример:
Решить уравнение 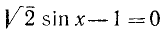
Решение:
sinх = 1 /]/2, откуда согласно (143.1) имеем х — 180°и + (—1)»45°, где я = 0, ±1, ±2, …
Пример:
Решить уравнение 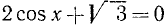
Решение:
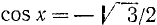
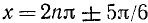
Пример:
Решить уравнение 3 sin х — 4 = 0.
Решение:
Из нашего уравнения получаем равносильное уравнение sin x = 4/3, которое решений не имеет, ибо не выполняется условие 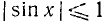
Пример:
Решить уравнение 3 tg х + 1 = 0.
Решение:
tg x = —1/3, откуда согласно (141.3) имеем 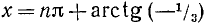
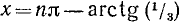
Замечание. Ответ можно записать так:
где n = 0, ±1, ±2, …
Пример:
Решить уравнение 3 ctg x + 2 = 0.
Решение:
ctg x = —2/3, откуда согласно (142.3) имеем 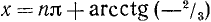
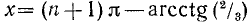
Пример:
Решить уравнение 2 sin 5x + l = 0.
Решение:
Записав уравнение в виде sin 5x = —1/2, найдем отсюда сначала промежуточный аргумент 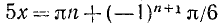
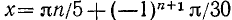
Видео:Решение тригонометрических уравнений и их систем. 10 класс.Скачать

Способ приведения к одной функции одного и того же аргумента
Сущность способа: Мы получили решения уравнений вида sin x = a, cos х = а, tg x = a и cxg x = a. Во многих случаях решение тригонометрических уравнений сводится к решению основных элементарных уравнений после выполнения ряда алгебраических действий.
Так, пусть имеется уравнение, левая часть которого содержит х только под знаком одной тригонометрической функции, например:
Во всех этих случаях задача решения уравнения распадается на две:
1) Решение алгебраического уравнения относительно новой неизвестной t = sin x, t = tg x, t = cos x.
2) Решение уравнений вида sin x = a, cos x = a, tg x = a.
Пример:
Решение:
1) Положив sin x = t, приходим к алгебраическому уравнению (в данном случае к квадратному уравнению) относительно новой неизвестной t:
Решив уравнение 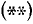
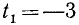
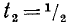
2) Задача решения уравнения 
Уравнение sin x = — 3 решений не имеет. Общее решение уравнения sin x = 1/2 имеет вид
Так как при переходе от тригонометрического уравнения 
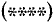
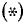
В большинстве случаев, однако, приходится исходное уравнение еще преобразовывать так, чтобы оно приобрело нужный вид:
В п. 145 показаны приемы таких преобразований.
Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента
1) Рассмотрим уравнение типа
где a, b и с — какие-то действительные числа. Изучим случай, когда 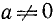
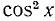
Заметим, что уравнения (145.1) и (145.2) будут равносильны, ибо мы предполагаем, что 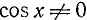
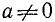
Пример:
Решение:
Разделим обе части уравнения на 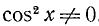
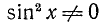
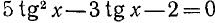
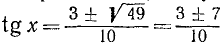
а) 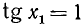
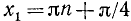
б) 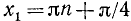
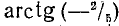
где п = 0, ±1, ±2, …
Замечание:
где 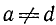
Пример:
Запишем данное уравнение так:
После этого будем иметь
Разделим обе части последнего уравнения на 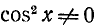
откуда 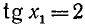
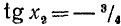
2) Рассмотрим уравнение типа
где a, b и с — какие-то действительные числа. Пусть 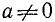
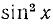
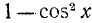
Из уравнения (145.6) находим возможные значения для t = соs x; естественно, что они будут иметь смысл лишь в случае 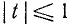
Решение. Заменяя 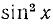
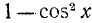
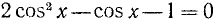
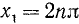
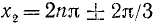
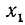
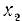
Пример:
Решение:
Заменив 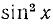
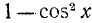
откуда cos x = 1/2 и cos x = —3/2. Последнее уравнение не имеет решений, ибо не выполнено условие 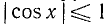
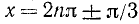
3) Рассмотрим уравнение тина
где a, b и с—какие-то действительные числа. Oграничимся рассмотрением примеров.
Пример:
Решение:
Заменив 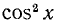
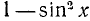
откуда sin x = 1/2 и sin x = —1/4. Оба последних уравнения имеют соответственно решения
Совокупность значений 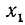
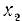
Пример:
Решение:
Заменив 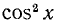
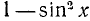
откуда 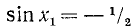

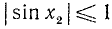
4) Рассмотрим уравнение типа
где 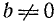
Деля обе части уравнения на 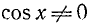
где n = 0, ±1, ±2, … Заметим, что, предположив 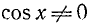
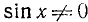
Пример:
Решение:
Разделим обе части уравнения на 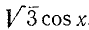
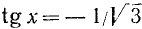
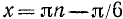
5) Если в уравнение входят тригонометрические функции от различных аргументов, то и в этом случае иногда представляется возможным выразить их все через одну тригонометрическую функцию одного и того же аргумента.
Пример:
Решение:
Заменив 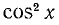
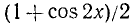
откуда cos 2х = — l/3.
Следовательно, 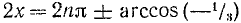
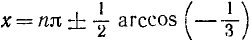
Пример:
Решить уравнение 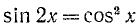
Решение:
Заменив sin 2x через 2sin x cos x, придем к уравнению 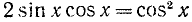
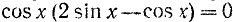
Первое уравнение имеет корни 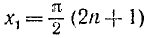
Второе уравнение после деления на 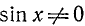
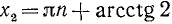
Решениями первоначального уравнения и будут значения 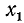
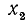
Пример:
Решение:
Умножим обе части уравнения на 2 и, заменив 2sin x cos x на sin 2х, получим sin 2x cos 2x = 1/4. С последним уравнением поступим опять так же, получим sin 4x = 1/2, откуда 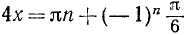
Пример:
Решение:
Подставив найденное значение для 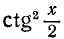
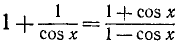
Последнее уравнение распадается на два:
Первое уравнение имеет корни 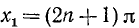
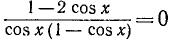
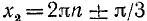
Способ разложения на множители
1) Если в уравнении, приведенном к виду f(x) = 0, его левая часть f(x) разлагается на множители, то, как указано в п. 54, следует приравнять каждый из этих множителей к нулю. Получится несколько отдельных уравнений; корни каждого из них будут корнями основного уравнения, если только они входят в о. д. з. каждого из множителей левой части уравнения.
Все полученные решения объединяются в одну совокупность решений первоначального уравнения. Заметим, что этот способ мы уже фактически применяли при решении примеров 9 и 11 из п. 145.
Рассмотрим е;це несколько примеров.
Пример:
Решить уравнение sin x ctg 2x = 0.
Решение:
Согласно предыдущему будем искать отдельно решения двух уравнений: a) sin x = 0 и б) ctg 2x = 0. Первое уравнение имеет корни 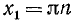
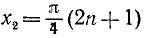
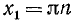
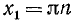
📹 Видео
Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Решение тригонометрических уравненийСкачать

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ решение примеров 10 классСкачать

Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

12 часов Тригонометрии с 0.Скачать

ЕГЭ №9. Тригонометрические выражения.Тригонометрические уравнения | Математика | TutorOnlineСкачать

10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

ТРИГОНОМЕТРИЯ ЗА 7 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

КАК РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ? // УРАВНЕНИЕ COSX=AСкачать