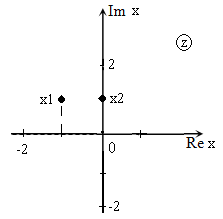Решение уравнений с комплексными корнями примеры (8 видео)

Решение уравнений с комплексными числами

Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.

Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:

где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = .

Пример 1. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа

Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.

Пример 2. Найти все корни уравнения

Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:

Найдем корни уравнения:

Ответ:

Пример 3. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа

Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = . Найдем модуль комплексного числа:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:

Пример 4. Найти корни уравнения

Решение кубического уравнения комплексными числами:

Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.

Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:

Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.

Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.

После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.

Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.

Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.

Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.

Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.

Содержание

Квадратное уравнение с комплексными корнями
Готовые работы на аналогичную тему
Примеры решений кубических уравнений
Пример решения кубического уравнения с комплексными корнями
Решение
Поиск целых корней
Сведение уравнения к приведенному виду
Определение вида корней
Нахождение корней по формуле Кардано
Ответ
Пример с действительными корнями
Решение
Поиск целых корней
Сведение уравнения к приведенному виду
Определение вида корней
Нахождение корней по формуле Виета
Ответ
📽️ Видео

Видео:Комплексные корни квадратных уравнений. 11 класс.Скачать

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ =8$.

Так как $A>0$, то $x_ =sqrt[] cdot left(cos frac +icdot sin frac right),, , , k=0. 2$.

При $k=0$ получаем $x_ =sqrt[] cdot left(cos 0+icdot sin 0right)=sqrt[] =2$.

При $k=1$ получаем

[x_ =sqrt[] cdot left(cos frac +icdot sin frac right)=sqrt[] cdot (-frac +frac <sqrt> cdot i)=2cdot (-frac +frac <sqrt> cdot i)=-1+sqrt cdot i.]

При $k=2$ получаем

[x_ =sqrt[] cdot left(cos frac +icdot sin frac right)=sqrt[] cdot (-frac -frac <sqrt> cdot i)=2cdot (-frac -frac <sqrt> cdot i)=-1-sqrt cdot i.]

Решить уравнение: $x^ =1+i$.

Готовые работы на аналогичную тему

Так как $A$ — комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

[varphi =arg z=arctgfrac =arctg1=frac ]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ =sqrt[] <sqrt> cdot left(cos frac +icdot sin frac right)=sqrt[] <sqrt> cdot left(cos frac +icdot sin frac right)=sqrt[] cdot left(cos frac +icdot sin frac right)$.

При $k=1$ получаем

При $k=2$ получаем

Квадратным называется уравнение вида $ax^ +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ -4ac$, при этом

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

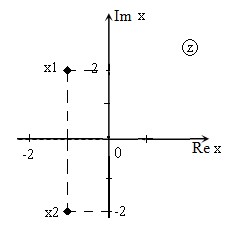
Решить уравнение $x^ +2x+5=0$ и изобразить корни на плоскости.

[D=2^ -4cdot 1cdot 5=4-20=-16.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ $ являются корнями квадратного уравнения $ax^ +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ )(x-x_ )=0$. В общем случае $x_ $ являются комплексными корнями.

Зная корни уравнения $x_ =1pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

[x^ -(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ -x+2icdot x-x-2icdot x+1-4i^ =0] [x^ -2x+1+4=0] [x^ -2x+5=0]

Следовательно, $x^ -2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ +(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 11 2021

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Работаем по будням с 10:00 до 20:00 по Мск

. и многие другие.
Успешной учебы! Будем рады вам помочь!

Видео:✓ Задача про комплексное число | Ботай со мной #101 | Борис ТрушинСкачать

Примеры решений кубических уравнений

Обзор методов решения кубических уравнений приведен на странице “Решение кубических уравнений”. Здесь мы приводим два примера, используя формулы Кардано и Виета.

Видео:Комплексные корни квадратного уравненияСкачать

Пример решения кубического уравнения с комплексными корнями

Решить кубическое уравнение:
(1.1) .

Решение

Поиск целых корней

Уравнение (1.1) имеет целые коэффициенты. Проверим, не содержит ли это уравнение целых корней. Член без – это 1. У числа 1 есть два делителя: 1 и – 1 . Подставим в уравнение (1.1) и . Ни для одного из этих чисел уравнение не выполняется. Следовательно, целых корней нет.

Сведение уравнения к приведенному виду

Пусть обозначают коэффициенты при , и свободный член. Делаем подстановку
(1.2) .
В результате получаем уравнение приведенного вида:
(1.3) ,
где
;
.

Определение вида корней

Определяем, имеет ли уравнение комплексные корни. Для этого находим дискриминант:
.
Дискриминант положителен. Следовательно, уравнение имеет один действительный корень и два комплексно сопряженных.

Нахождение корней по формуле Кардано

Поскольку дискриминант положителен, то находим корни по формуле Кардано:
, ,
где
; ; .
При , для величин и , можно взять действительные значения корней. Тогда соотношение выполняется автоматически.

Итак, мы нашли корни неполного кубического уравнения. По формуле (1.2) находим корни исходного уравнения:
.

Ответ

Видео:Уравнение с комплексными числамиСкачать

Пример с действительными корнями

Решить кубическое уравнение:
(2.1) .

Решение

Поиск целых корней

Уравнение (2.1) имеет целые коэффициенты. Проверим, нет ли у этого уравнения целых корней. Свободный член – это 1. У него есть два делителя: 1 и – 1 . Подставим в уравнение (2.1) и . Уравнение не выполняется ни для одного из этих чисел. Следовательно, целых корней нет.

Сведение уравнения к приведенному виду

В исходном уравнении (2.1),
.
Делаем подстановку
(2.2)
и приводим уравнение (2.1) к приведенному (неполному) виду:
(2.3) ,
где
;
.

Определение вида корней

Определяем, имеет ли уравнение комплексные корни. Находим дискриминант:
.
Дискриминант отрицателен. Следовательно, уравнение имеет три действительных корня.

Нахождение корней по формуле Виета

Итак, мы нашли корни приведенного кубического уравнения. По формуле (2.2) находим корни исходного уравнения:
.

Ответ

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.

Автор: Олег Одинцов . Опубликовано: 02-10-2016