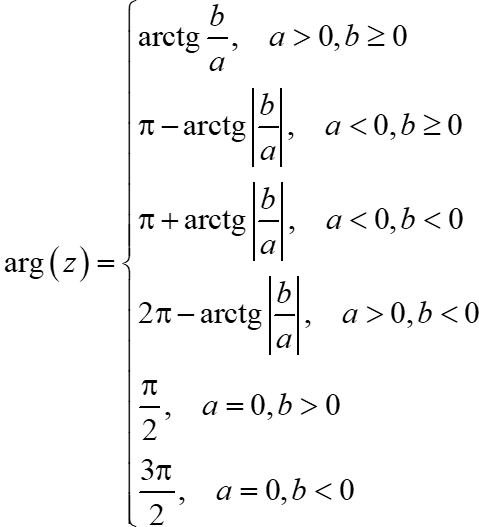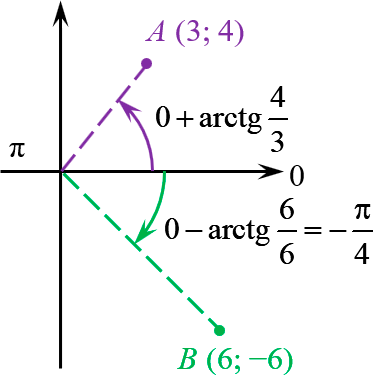Решение уравнений с комплексными числами тригонометрические функции

Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.

Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:

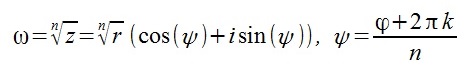
где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = .

Пример 1. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа

Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:

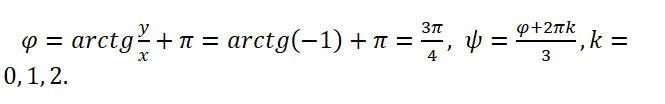
Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.

Пример 2. Найти все корни уравнения

Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:

Найдем корни уравнения:

Ответ:

Пример 3. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа

Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = . Найдем модуль комплексного числа:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:

Пример 4. Найти корни уравнения

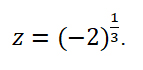
Решение кубического уравнения комплексными числами:

Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.

Найдем все необходимые значения для формулы:

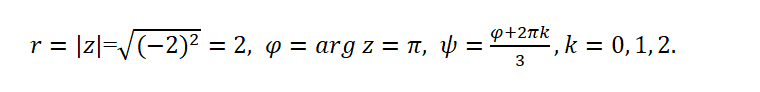
Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:

Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.

Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.

После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.

Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.

Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.

Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.

Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.

Видео:Тригонометрическое уравнение: cos(z)=2, а при чём тут формула Эйлера?Скачать

Комплексные числа и их приложение к решению уравнений третьей и четвертой степени (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

КОМПЛЕКСНЫЕ ЧИСЛА И ИХ

ПРИЛОЖЕНИЕ К РЕШЕНИЮ

И ЧЕТВЕРТОЙ СТЕПЕНИ

Учебное пособие для студентов

кандидат физико-математических наук, доцент

Комплексные числа и их приложение к решению уравнений 3-й и 4-й степени. Учебное пособие для студентов физико-математического факультета / сост.: – Воронежский госпедуниверситет, 2010. – 92 с.

Учебное пособие представляет собой курс лекций и практических занятий по теме «Комплексные числа». Пособие делится на четыре части: комплексные числа в алгебраической форме, геометрическая интерпретация комплексных чисел, комплексные числа в тригонометрической форме, приложение теории комплексных чисел к решению кубических уравнений и уравнений 4-й степени. В заключение приводится краткий исторический обзор формирования понятия комплексного числа и действий над комплексными числами.

Предназначено для студентов физико-математического факультета Воронежского госпедуниверситета.

Теория комплексных чисел является составной частью курса «Высшая алгебра» в педагогических вузах и предполагает глубокое знание ее основ, а также методов и приемов, применяемых при решении широкого класса задач как алгебраического, так и геометрического содержания. Будущие учителя должны грамотно и непринужденно оперировать с основными понятиями, действиями и интерпретациями комплексных чисел, поскольку азы теории комплексных чисел являются частью учебной программы по математике для профильных классов. Это объясняется тем, что, будучи непосредственным обобщением понятия действительного числа, комплексное число является завершающим элементом в стройной и строгой логической
конструкции понятия числа.

Алгебраическая природа комплексного числа состоит в том, что комплексное число есть элемент алгебраического расширения С поля действительных чисел R , получаемого присоединением к полю R корня i многочлена f(x) = x2 + 1 . Получающееся таким путем поле С называется полем комплексных чисел.

Наиболее важное свойство комплексных чисел состоит в том, что оно алгебраически замкнуто, т. е. любой многочлен с коэффициентами из С разлагается на линейные множители. Иначе это свойство алгебраической замкнутости выражается в том, что любой многочлен степени n ≥ 1 с коэффициентами из С имеет в поле комплексных чисел по крайней мере один корень (теорема Даламбера – Гаусса).

Изучение теории комплексных чисел выполняет следующие образовательные функции.

1) Расширение математического кругозора и повышение математической культуры учащихся.

Наличие у комплексных чисел более тесной, нежели у других числовых множеств, связи с геометрией (в частности, с векторным исчислением) представляет широкие возможности, с одной стороны, применения алгебраических методов к решению геометрических
задач (задачи на построение ГМТ), а с другой стороны, наглядных геометрических интерпретаций различных алгебраических операций (действий с комплексными числами в тригонометрической форме).

2) Логическое завершения развития понятия числа.

3) Выделение из множества всех алгебраических уравнении лишь тех, которые решаются в радикалах, т. е. для которых существуют формулы, выражающие корни уравнения через его коэффициенты.

Сюда относится решение уравнений 3-й степени (и сводящихся к ним уравнений 4-й степени), поскольку по теореме Абеля: «Ни для какого натурального числа нельзя указать формулу, которая выражала бы корни любого уравнения п-й степени через его коэффициенты при помощи радикалов».

В первой главе пособия сначала вводится понятие комплексного числа в алгебраической форме, определяются операции сложения, вычитания, умножения, деления, а также операция сопряжения для комплексных чисел в алгебраической форме; излагается правило извлечения квадратного корня из комплексного числа.

Во второй главе изучается геометрическая интерпретация комплексных чисел в виде точек или векторов комплексной плоскости.

В третьей главе рассмотрены действия над комплексными числами в тригонометрической форме.

Четвертая глава посвящена решению уравнений 3-й и 4-й степеней.

Завершает пособие краткая историческая справка о возникновении понятия комплексного числа.

Особенностью изложения материала является форма в виде лекционных и практических занятий. Эта форма выбрана для удобства использования представленного материала как преподавателями, так и студентами. В конце каждой из первых трех глав приведены примерные варианты контрольных работ.

Глава 1. КОМПЛЕКСНЫЕ ЧИСЛА В АЛГЕБРАИЧЕСКОЙ ФОРМЕ

Занятие 1. Введение понятия комплексного числа.

Сложение, вычитание, умножение и деление комплексных чисел. Степени мнимой единицы

Понятие числа прошло длинный исторический путь. В процессе развития математики числовая система расширялась не один раз. Уже на ранних этапах развития человечества в результате счета возникают натуральные числа. Постепенно складывается представление о бесконечности множества натуральных чисел и появляется понятие натурального ряда бесконечной последовательности чисел 1, 2, 3, 4, 5, . . Затем возникают дроби, нуль, отрицательные числа, необходимые для
решения линейных уравнений вида

Поскольку рациональных чисел было достаточно для того, чтобы с любой степенью точности выразить результат любого измерения, то долгое время считали, что результат измерения всегда выражается или натуральным числом, или отношением двух таких чисел, т. е. дробью.

Однако еще в школе Пифагора был обнаружен тот факт, что диагональ квадрата несоизмерима с его стороной и поэтому не может быть точно выражена рациональным числом. Это открытие привело в конце концов к тому, что в математику вошли иррациональные числа.

Рациональные числа вместе с иррациональными образуют множество действительных чисел, которое является расширением множества рациональных чисел, поскольку на нем также определены четыре арифметических действия: сложение, вычитание, умножение и деление (кроме деления на нуль).

Важное место в алгебре занимает решение алгебраических уравнений, т. е. уравнений вида

,

где а0, а1, . . . , аn — действительные числа. Однако оказалось, что для решения таких уравнений действительных чисел явно не достаточно. Например, действительных корней не имеет квадратное уравнение с отрицательным дискриминантом. Простейшим таким уравнением является уравнение

Для того чтобы это уравнение имело решение, необходимо расширить множество действительных чисел путем присоединения к нему корня уравнения

Обозначим этот корень через i. Таким образом, по определению

Символ i называется мнимой единицей. С его помощью и с помощью пары действительных чисел а и b составляется выражение вида

Полученные выражения назвали комплексными числами, поскольку они содержали как действительную, так и мнимую части (от французских слов rее1 – действительный и imaginaire – мнимый, воображаемый). Название комплексное переводится как составное — по виду выражения z = a+bi.

Итак, комплексными числами называются выражения вида

где а и b – действительные числа, а i – некоторый символ,
удовлетворяющий условию i= . Число а называется
действительной частью комплексного числа z=a+bi, а
число b его мнимой частью. Для их обозначения используются символы

Комплексные числа вида z=a+0∙i=а являются
действительными числами и, следовательно, множество комплексных чисел содержит в себе множество действительных чисел. Если потребовать, как мы сделаем это ниже, чтобы операции сложения и умножения комплексных чисел не выводили за пределы множества комплексных чисел и обладали всеми свойствами одноименных операций на множестве действительных чисел, то множество комплексных чисел будет расширением множества действительных чисел.

Комплексные числа вида z=0+bi называются чисто
мнимыми.

Два комплексных числа z1=a1+b1i и z2=a2+b2i
называются равными, если равны их действительные и мнимые части, т. е. если выполняются равенства

Определим операции сложения и умножения комплексных чисел.

Суммой двух комплексных чисел и называется комплексное число вида

.

Произведение двух комплексных чисел z1=a1+b1i и z2=a2+b2i можно найти, почленно умножая числа z1 и z2:

.

Таким образом, произведением двух комплексных чисел z1=a1+b1i и z2=a2+b2i называется комплексное число z1 ∙ z2 вида

.

Пример. Найдите сумму комплексных чисел z1= 2 + 3i и z2= –3 – i.

Пример. Найдите произведение комплексных чисел z1= 2 + 3i и z2= –1 – i .

Свойства операций сложения и умножения комплексных чисел

Каковы бы ни были комплексные числа , справедливы следующие равенства.

1. Коммутативный (переместительный) закон сложения:

.

2. Ассоциативный (сочетательный) закон сложения:

.

3. Коммутативный закон умножения:

.

4. Ассоциативный закон умножения:

.

5. Дистрибутивный (распределительный) закон умножения относительно сложения:

.

Проведем доказательство свойства 3 (остальные свойства доказываются аналогично).

Доказательство. Пусть , . Тогда поскольку а1 , b1 , a2 и b2 – действительные числа, для которых умножение коммутативно, получаем:

Кроме того, в множестве комплексных чисел есть «особые» элементы

0 = 0 + 0i и 1= l + 0i ,

которые обладают такими же свойствами, что и на множестве действительных чисел, а именно, для любого комплексного числа z = а + bi имеют место равенства:

8. Произведение двух комплексных чисел равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю.

Доказательство. Пусть , и . Тогда по определению равенства и произведения двух комплексных чисел получаем систему уравнений :

Умножив уравнение (1) на а2 , а уравнение (2) на b2 и сложив полученные уравнения, приходим к системе :

Возможны два случая.

Тогда из уравнения (1)* следует, что b1b2 = 0.
a) Если b1 = 0 , а b2 ≠ 0, то z1 = a1 + b1i = 0.
б) Если b2 = 0 , а b1 ≠ 0 то из уравнения (2) следует, что a2b1 = 0 , значит, а2 = 0 , т. е. z2 = a2 + b2i = 0.

в) Если b1 = b2 = 0 , то z1 = 0 .

Тогда из уравнения (2)* следует, что, a22 + b22 = 0 , т. е. а2 = b2 = 0 , значит, z2 = 0.

10. Любому комплексному числу z=а+bi соответствует противоположное комплексное число (–z) такое, что z + (–z) = 0 .

11. Всякому комплексному числу z=а+bi, отличному от нуля, соответствует обратное комплексное число z–1 такое, что z ∙ z–1 = 1 .

Доказательство. Условие z ≠ 0 равносильно условию а2 + b2 > 0 . Вычислим z–1.

.

Пользуясь понятиями противоположного и обратного комплексного числа, определим операции вычитания и деления комплексных чисел.

Для того чтобы найти разность двух комплексных чисел и , достаточно сложить число z1 с числом, противоположным числу z2 , т. е.

.

Пример. Вычислите z1 – z2 , если z1 = 5 – 2i ,

Для того чтобы разделить комплексное число на комплексное число , не равное нулю, достаточно умножить число z1 на число, обратное числу z2 , т. е.

Пример. Вычислите .

.

Видео:Комплексные числа и "золотое" уравнениеСкачать

Степени мнимой единицы

Вычислим степени мнимой единицы i. Прежде всего, как и для действительных чисел, положим i0 = 1 . Тогда

i2 = –1 (по определению мнимой единицы);

Вообще, если натуральный показатель степени mпри делении на 4 дает в остатке r , т. е. если m = 4n+r , где n – натуральное число, то

;

Пример. Вычислите а) i233 ; b) i102; с) i67 ; d) i516.

Решение. а) i233 = i232 + 1 = i ;

Занятие 2. Операция сопряжения и ее свойства.

Видео:Тригонометрическая форма комплексного числаСкачать

Модуль комплексного числа.

Извлечение корня квадратного из комплексного числа

Комплексное число называется сопряженным комплексному числу, если

.

Пример. .

Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Свойства операции сопряжения

2. Для любого действительного числа а справедливо равенство .

3. Для любого действительного числа b справедливо равенство .

Справедливость свойств 1-3 следует непосредственно из определения операции сопряжения.

4. .

Доказательство. Пусть , . Тогда , . Поэтому

.

Доказательство. Пусть , . Тогда

С другой стороны,

.

Полученные одинаковые результаты доказывают справедливость свойства 5 .

Следствие из свойства 5. Для любого натурального числа n справедливо равенство

.

6. .

Справедливость данного равенства следует из равенства и свойства 5: .

7. Сумма и произведение двух комплексно сопряженных чисел являются действительными числами.

.

Модулем комплексного числа z = а + bi называется действительное число вида

.

Непосредственно из свойства 7 следует, что

.

8. Теорема о сопряженном корне.

Если число является корнем уравнения

(1)

с действительными коэффициентами а0, a1 , . . . , аn , то число также является корнем уравнения (1) .

Доказательство. По определению корня имеем :

;

(2)

Применим к обеим частям равенства (2) операцию сопряжения. Из свойств операции сопряжения следует, что

так как все коэффициенты ai — действительные числа (по условию). Кроме того,

; .

.

Последнее равенство означает, что число z = а – bi является корнем уравнения (1) .

Пример. Зная, что корнем уравнения

является число z1 = 2 + i , найти все корни данного уравнения.

Решение. Поскольку все коэффициенты уравнения (3) – действительные числа, то на основании теоремы 8 делаем вывод, что число z2 = 2 – i также является корнем уравнения (3).

Пусть z3 – неизвестный корень уравнения (3), тогда

Разделив обе части последнего равенства на х2 – 4х + 5 , получим

Следовательно, z3 = 3 .

Найдем значение корня квадратного из числа z=а+bi . Пусть

,

где х и у — неизвестные действительные числа. Возводя обе части этого равенства в квадрат, получаем:

.

Последнее уравнение равносильно системе уравнений

Возведем каждое уравнение системы в квадрат и сложим полученные равенства. Решим систему:

Из второго уравнения последней системы находим

,

где в правой части равенства следует иметь в виду арифметический корень, так как сумма х2+у2 неотрицательна. Учитывая, кроме того, что х2 –­­ у2 = а , получаем:

.

Так как , то оба полученные числа положительны. Извлекая из них квадратные корни, получим действительные значения для х и у :

.

Видео:Уравнение с комплексными числамиСкачать

Тригонометрическая форма комплексных чисел

Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».

Сегодня мы узнаем:

Начнём с ключевого определения.

Видео:Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

1. Тригонометрическая форма

Определение. Тригонометрическая форма комплексного числа — это выражение вида

[z=left| z right|cdot left( cos text!!varphi!!text+isin text!!varphi!!text right)]

где $left| z right|$ — модуль комплексного числа, $text!!varphi!!text$ — некоторый угол, который называется аргумент комплексного числа (пишут $text!!varphi!!text=arg left( z right)$).

Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:

Записать в тригонометрической форме число $z=sqrt+i$.

Переписываем исходное число в виде $z=sqrt+1cdot i$ и считаем модуль:

Выносим модуль за скобки:

[z=sqrt+1cdot i=2cdot left( frac<sqrt>+fraccdot i right)]

Вспоминаем тригонометрию, 10-й класс:

Понятно, что вместо $frac<text!!pi!!text>$ с тем же успехом можно взять аргумент $frac<13text!!pi!!text>$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:

Записать в тригонометрической форме число $z=-1-i$.

Видео:Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

2. Умножение и деление комплексных чисел

Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.

Теорема. Пусть даны два комплексных числа:

[begin & <_>=left| <_> right|cdot left( cos alpha +isin alpha right) \ & <_>=left| <_> right|cdot left( cos beta +isin beta right) \ end]

Тогда их произведение равно

[<_>cdot <_>=left| <_> right|cdot left| <_> right|cdot left( cos left( alpha +beta right)+isin left( alpha +beta right) right)]

А если ещё и $left| <_> right|ne 0$, то их частное равно

Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!

Найти произведение и частное двух комплексных чисел:

[begin <_>cdot <_> & =2cdot 5cdot left( cos left( frac+frac right)+isin left( frac+frac right) right)= \ & =10cdot left( cos frac+isin frac right) \ end]

[begin frac<<_>><<_>> & =fraccdot left( cos left( frac-frac right)+isin left( frac-frac right) right)= \ & =0,4cdot left( cos frac+isin frac right) \ end]

По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)

Видео:Решение уравнений с комплексными числамиСкачать

3. Формула Муавра

Пусть дано комплексное число в тригонометрической форме:

[z=left| z right|cdot left( cos text!!varphi!!text+isin text!!varphi!!text right)]

Возведём его в квадрат, умножив на само себя:

[begin <^> & =zcdot z = \ & =left| z right|left| z right|cdot left( cos left( text!!varphi!!text!!varphi!!text right)+isin left( text!!varphi!!text!!varphi!!text right) right)= \ & =<^>cdot left( cos 2text!!varphi!!text+isin 2text!!varphi!!text right) \ end]

Затем возведём в куб, умножив на себя ещё раз:

Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.

Формула Муавра. При возведении всякого комплексного числа

[z=left| z right|cdot left( cos varphi +isin varphi right)]

в степень $nin mathbb$ получим

Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $nin mathbb$, а не только натуральном. Но об этом позже. Сейчас примеры:

Представим первое число в тригонометрической форме:

[begin sqrt-i & = 2cdot left( frac<sqrt>+icdot left( -frac right) right)= \ & =2cdot left( cos left( -frac right)+isin left( -frac right) right) \ end]

По формуле Муавра:

Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.

Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:

Теперь второе число запишем в комплексной форме:

По формуле Муавра:

Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.

Видео:Комплексные числа в уравненияхСкачать

4. Дополнение 1. Геометрический подход

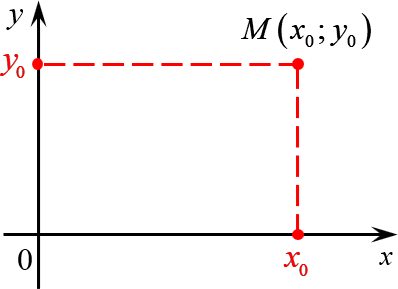
Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:

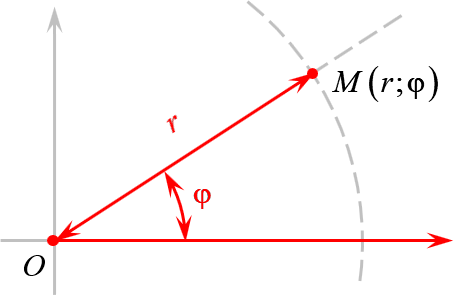
А есть полярная система координат, где точки задаются поворотом на угол $varphi $ и расстоянием до центра $r$:

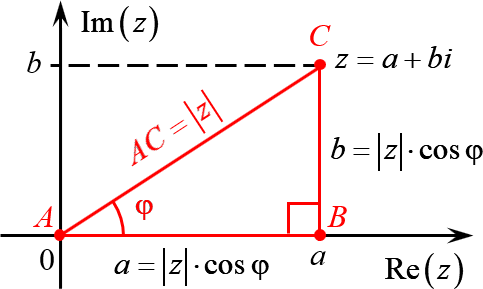
А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:

Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние

Треугольник $ABC$ — прямоугольный. Пусть $angle BAC=varphi $. Тогда:

[begin & AB=ACcdot cos varphi =left| z right|cdot cos varphi \ & BC=ACcdot sin varphi =left| z right|cdot sin varphi \ end]

С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:

[begin a+bi & =left| z right|cos varphi +icdot left| z right|sin varphi = \ & =left| z right|left( cos varphi +isin varphi right) \ end]

Итак, мы перешли от пары $left( a;b right)$ к паре $left( left| z right|;varphi right)$, где $left| z right|$ — модуль комплексного числа, $varphi $ — его аргумент (проще говоря, угол поворота).

Важное замечание. А кто сказал, что такой угол $varphi $ существует? Возьмём число $z=a+bi$ и вынесем модуль за скобку:

Осталось подобрать такой угол $varphi $, чтобы выполнялось два равенства:

Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:

На практике основная трудность заключается именно в поиске подходящего аргумента.

Видео:✓ Задача про комплексное число | Ботай со мной #101 | Борис ТрушинСкачать

5. Дополнение 2. Как найти аргумент?

В учебниках пишут много разной дичи, типа вот этой:

Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.

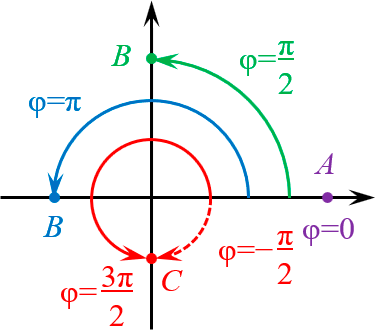
5.1. Точки на координатных осях

Для начала рассмотрим точки, лежащие осях координат.

Тут всё очевидно:

• На положительной полуоси абсцисс $varphi =0$ (фиолетовая точка $A$).
• На отрицательной — $varphi =pi $ (синяя точка $B$).
• На положительной полуоси ординат $varphi =frac$ (зелёная точка $B$).
• На отрицательной — $varphi =frac$ (красная точка $C$). Однако ничто не мешает рассмотреть $varphi =-frac$ — результат будет тем же самым.:)

5.2. Точки с арктангенсом

А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $ane 0$ и $bne 0$. Рассмотрим вспомогательный угол

Очевидно, это острый угол:

Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол $<_>$ от горизонтальной оси в эту четверть.

В правой полуплоскости мы откладываем от «нулевого» луча:

Точка $Aleft( 3;4 right)$ удалена от начала координат на расстояние 5:

[begin 3+4i & =5cdot left( cos varphi +isin varphi right) \ varphi & =operatornamefrac end]

Для точки $Bleft( 6;-6 right)$ арктангенс оказался табличным:

[6-6i=6sqrtcdot left( cos left( -frac right)+isin left( -frac right) right)]

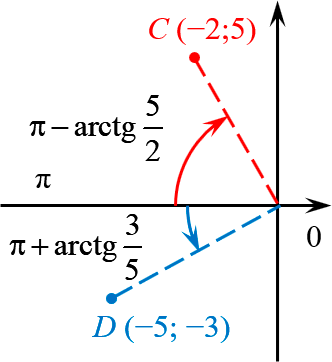
В левой полуплоскости откладываем от луча, соответствующего углу $pi $:

Итого для точки $Cleft( -2;5 right)$ имеем:

[begin -2+5i & =sqrtcdot left( cos varphi +isin varphi right) \ varphi & =pi -operatornamefrac end]

И, наконец, для точки $Dleft( -5;-3 right)$:

[begin -5-3i & =sqrtcdot left( cos varphi +isin varphi right) \ varphi & =pi +operatornamefrac end]

Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.

А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)

🎦 Видео

Высшая математика. Комплексные числаСкачать

Комплексные корни квадратного уравненияСкачать

Формула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать

Изобразить область на комплексной плоскостиСкачать

10 класс, 34 урок, Тригонометрическая форма записи комплексного числаСкачать

Комплексные числа. Тригонометрическая форма. Формула Муавра | Ботай со мной #040 | Борис Трушин !Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Математика без Ху!ни. Комплексные числа, часть 2. Простейшие действия.Скачать

Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать
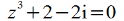
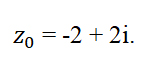
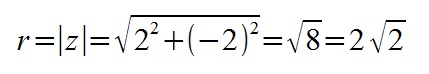
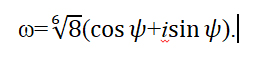
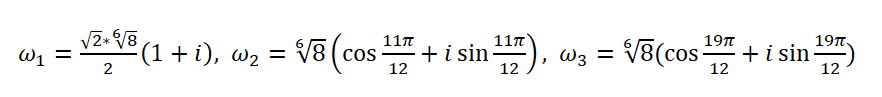
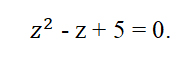
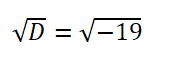
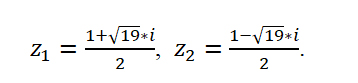
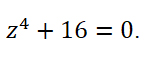
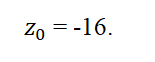
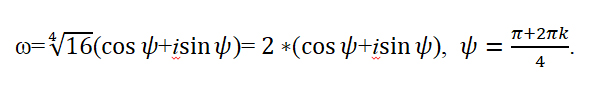
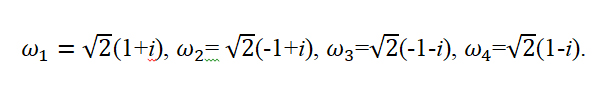
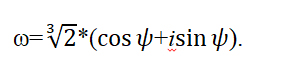
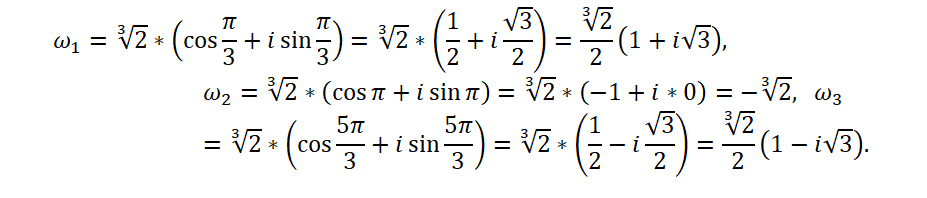
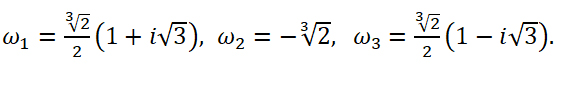