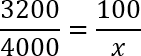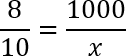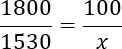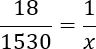Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции
Данные задачи на проценты можно записать в виде следующих соотношений:
все — 100% часть — часть в %
которые можно записать в виде пропорции
| все | = | 100% |
| часть | часть в % |
Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.
- Примеры решения задач на проценты
- Задачи на проценты: считаем проценты с помощью пропорции
- Задача B2 на проценты №2
- Как решать задачи с процентами
- Основные определения
- Типы задач на проценты
- Тип 1. Нахождение процента от числа
- Тип 2. Нахождение числа по его проценту
- Тип 3. Нахождение процентного отношения двух чисел
- Тип 4. Увеличение числа на процент
- Тип 5. Уменьшение числа на процент
- Тип 6. Задачи на простые проценты
- Тип 7. Задачи на сложные проценты
- Задачи на проценты с решением
- 🌟 Видео
Видео:Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Примеры решения задач на проценты
30 соответствует 100% x соответствует 15%
| 30 | = | 100% |
| x | 15% |
решим полученное уравнение
| x = | 30 · 15% | = 4.5 |
| 100% |
Ответ: 15% от 30 равно 4.5.
20 соответствует 100% 35 соответствует x
| 20 | = | 100% |
| 35 | x |
решим полученное уравнение
| x = | 35 · 100% | = 175% |
| 20 |
Ответ: 35 составляет 175% от 20.
x соответствует 100% 20 соответствует 5%
| x | = | 100% |
| 20 | 5% |
решим полученное уравнение
| x = | 20 · 100% | = 400 |
| 5% |
Ответ: 400.
При изучении процентов вам также будут полезны:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Решение уравнений, 6 классСкачать

Задачи на проценты: считаем проценты с помощью пропорции
В прошлом видеоуроке мы рассматривали решение задач на проценты с помощью пропорций. Тогда по условию задачи нам требовалось найти значение той или иной величины.
В этот раз исходное и конечное значения нам уже даны. Поэтому в задачах будет требоваться найти проценты. Точнее, на сколько процентов изменилась та или иная величина. Давайте попробуем.
Задача. Кроссовки стоили 3200 рублей. После повышения цены они стали стоить 4000 рублей. На сколько процентов была повышена цена на кроссовки?
Итак, решаем через пропорцию. Первый шаг — исходная цена была равна 3200 рублей. Следовательно, 3200 рублей — это 100%.
Кроме того, нам дана конечная цена — 4000 рублей. Это неизвестное количество процентов, поэтому обозначим его за x . Получим следующую конструкцию:
3200 — 100%
4000 — x %
Что ж, условие задачи записано. Составляем пропорцию:
Дробь слева прекрасно сокращается на 100: 3200 : 100 = 32; 4000 : 100 = 40. Кроме того, можно сократить на 4: 32 : 4 = 8; 40 : 4 = 10. Получим следующую пропорцию:
Воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних. Получаем:
8 · x = 100 · 10;
8 x = 1000.
Это обычное линейное уравнение. Отсюда находим x :
x = 1000 : 8 = 125
Итак, мы получили итоговый процент x = 125. Но является ли число 125 решением задачи? Нет, ни в коем случае! Потому что в задачи требуется узнать, на сколько процентов была повышена цена на кроссовки.
На сколько процентов — это значит, что нам нужно найти изменение:
Получили 25% — именно настолько была повышена исходная цена. Это и является ответом: 25.
Видео:Решение задач на проценты способом пропорции. 6 класс.Скачать

Задача B2 на проценты №2
Переходим ко второй задаче.
Задача. Рубашка стоила 1800 рублей. После снижения цены она стала стоить 1530 рублей. На сколько процентов была снижена цена на рубашку?
Переводим условие на математический язык. Исходная цена 1800 рублей — это 100%. А итоговая цена 1530 рублей — она нам известна, но неизвестно, сколько процентов она составляет от исходной величины. Поэтому обозначим ее за x . Получим следующую конструкцию:
1800 — 100%
1530 — x %
На основе полученной записи составляем пропорцию:
Давайте для упрощения дальнейших вычислений разделим обе части данного уравнения на 100. Другими словами, у числителя левой и правой дроби мы зачеркнем два нуля. Получим:
Теперь снова воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних.
18 · x = 1530 · 1;
18 x = 1530.
Осталось найти x :
x = 1530 : 18 = (765 · 2) : (9 · 2) = 765 : 9 = (720 + 45) : 9 = 720 : 9 + 45 : 9 = 80 + 5 = 85
Как видите, мы не стали считать полученное частное уголком, а просто несколько раз сократили нашу дробь. При этом нам потребовалось разложить на множители числитель и
Мы получили, что x = 85. Но, как и в прошлой задаче, это число само по себе не является ответом. Давайте вернемся к нашему условию. Теперь мы знаем, что новая цена, полученная после снижения, составляет 85% от старой. И для того, чтобы найти изменения, нужно из старой цены, т.е. 100%, вычесть новую цену, т.е. 85%. Получим:
Это число и будет ответом: Обратите внимание: именно 15, а ни в коем случае не 85. Вот и все! Задача решена.
Внимательные ученики наверняка спросят: почему в первой задаче мы при нахождении разности вычитали из конечного числа начальное, а во второй задаче поступили в точности до наоборот: из исходных 100% вычли конечные 85%?
Давайте проясним этот момент. Формально, в математике изменением величины всегда называется разность между конечным значением и начальным. Другими словами, во второй задаче у нас должно было получиться не 15, а −15.
Однако этот минус ни в коем случае не должен попасть в ответ, потому что он уже учтен в условии исходной задачи. Там прямо сказано о снижении цены. А снижение цены на 15% — это то же самое, что повышение цены на −15%. Именно поэтому в решении и ответе задачи достаточно написать просто 15 — без всяких минусов.
Все, надеюсь, с этим моментом мы разобрались. На этом наш сегодняшний урок закончен. До новых встреч!
Видео:Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Как решать задачи с процентами
О чем эта статья:
Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Основные определения
Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.
Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».
Процент — это одна сотая часть от любого числа. Обозначается вот так: %.
Как перевести проценты в десятичную дробь? Нужно убрать знак % и разделить число на 100. Например, 18% — это 18 : 100 = 0,18.
А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:
Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а потом используем предыдущее правило и переведем десятичную дробь в проценты:
Видео:Решить уравнение - Математика - 6 классСкачать

Типы задач на проценты
В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.
Тип 1. Нахождение процента от числа
Чтобы найти процент от числа, нужно число умножить на процент.
Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?
Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).
Ответ: из общего количества изготовленных стульев контроль не прошли 100 штук.
Тип 2. Нахождение числа по его проценту
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.
Задача. Школьник решил 40 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?
Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 40 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.
40 : 0,16 = 40 · 100 : 16 = 250
Ответ: 250 задач собрано в этом учебнике.
Тип 3. Нахождение процентного отношения двух чисел
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.
Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?
Как решаем: поделим 10 на 25, полученную дробь переведем в проценты.
10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%
Ответ: в классе 40% девочек.
Тип 4. Увеличение числа на процент
Чтобы увеличить число на некоторое количество процентов, можно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.
А можно воспользоваться формулой:
a = b · (1 + с : 100),
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом месяце стикерпак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикерпак?
Как решаем: можно найти 12% от 110:
Прибавить к исходному числу:
110 + 13,2 = 123,2 рубля.
Или можно воспользоваться формулой, тогда:
110 · (1 + 12 : 100) = 110 · 1,12 = 123,2.
Ответ: стоимость стикерпака в этом месяце — 123 рубля 20 копеек.
Тип 5. Уменьшение числа на процент
Чтобы уменьшить число на несколько процентов, можно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.
А можно воспользоваться формулой:
a = b · (1 − с : 100),
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом году школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?
Как решаем: можно найти 25% от 100:
Вычесть из исходного числа 100 − 25 = 75 человек.
Или можно воспользоваться формулой, тогда:
100 · (1 − 25 : 100) = 75/p>
Ответ: 75 выпускников в этом году.
Тип 6. Задачи на простые проценты
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.
Формула расчета выглядит так:
S = а · (1 + у · х : 100),
где a — исходная сумма,
S — сумма, которая наращивается,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Марии срочно понадобились деньги и она взяла на один год в долг 70 000 рублей под 8% ежемесячно. Сколько денег она вернет через год?
Как решаем: подставим в формулу данные из условий задачи.
70 000 · (1 + 12 · 8 : 100) = 137 200
Ответ: 137 200 рублей вернет Мария через год.
Тип 7. Задачи на сложные проценты
Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.
Формула расчета выглядит так:
S = а · (1 + х : 100) y ,
где S — наращиваемая сумма,
a — исходная,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Антон хочет оформить вклад 10 000 рублей на 5 лет в банке, который дает 10% годовых. Какую сумму снимет Антон через 5 лет хранения денег в этом банке?
Как решаем: просто подставим в формулу данные из условий задачи:
10000 · (1 + 10 : 100)3 = 13 310
Ответ: 13 310 рублей снимет Антон через год.
Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!
Есть случаи, когда найти процент от числа проще, если представить проценты в виде простых дробей. В таком случае будем искать часть числа.
- 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
- 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
- 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
- 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
- 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Как решаем:
|
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Видео:Как решают уравнения в России и СШАСкачать

Задачи на проценты с решением
Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.
Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?
Ответ: масса воды 53,2 кг
Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?
Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.
Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:
0,6х — 0,25 * 0,6x = 0,45x
После двух понижений изменение цены составит:
Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.
Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?
По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто
Получается, что стоимость одной пары брюк — это 23% стоимости пальто.
Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.
Ответ: пять пар брюк на 15% дороже, чем одно пальто.
Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.
По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.
Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.
Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.
А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.
Ответ: заработок жены составляет 27%.
Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.
Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.
Значит, 19 килограммов питательного вещества в абрикосах — это 10% веса свежих абрикосов. Найдем число по проценту.
Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.
🌟 Видео
КАК РЕШАТЬ ПРОПОРЦИИ?Скачать
Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Решить уравнение с дробями - Математика - 6 классСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

РЕШЕНИЕ УРАВНЕНИЙ ЛЕГКО ! 1 КЛАСС МАТЕМАТИКА УРАВНЕНИЯ - ПЕТЕРСОН / ОБЪЯСНЕНИЕ КАК РЕШАТЬ УРАВНЕНИЯСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

решить уравнение относительно хСкачать

Решение уравнений - математика 6 классСкачать

Задача на проценты - три способа решенияСкачать

Сложные уравнения. Как решить сложное уравнение?Скачать

ОГЭ по математике. Решаем уравнения | МатематикаСкачать