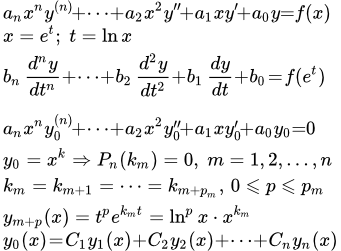Функция Эйлера, это функция, которая равна количеству натуральных чисел, меньших m и взаимно простых с m. Предполагается, что число 1 взаимно просто со всеми натуральными числами (и с единицею). Обозначается функция Эйлера греческой буквой φ.
Возьмем ряд натуральных чисел до m
| 1, 2, 3, . m. |
Определим, сколько в этом ряду чисел, взаимно простых с m. Так как единица взаимно простое с единицею, то
Далее, число 2 взаимно просто с 1, тогда φ(2)=1, число 3 взаимно просто с 1 и 2, тогда φ(3)=2. Продолжая получим: φ(4)=2, φ(5)=4, и т.д.
Сформулируем следующие задачи.
Задача 1. Пусть a1, a2, a3, . все отличные друг от друга простые множители числа m. Найти число тех чисел, которые не делятся ни на одно из чисел a1, a2, a3, . .
Более общая задача имеет следующий вид:
Задача 2. Пусть a1, a2, a3, . взаимно простые числа, которые входят множителями в m. Найти число всех чисел, которые не делятся ни на одно из чисел a1, a2, a3, . .
Возьмем ряд натуральных чисел до m:
| 1, 2, 3, . m. | (1) |
Исключим из ряда (1) все те числа, которые делятся на a1. Это следующие числа
 |
Их число равно 
 | (2) |
числа, которые не делятся на a1. Обозначим множество этих чисел через A1.
Из чисел ряда A1 нужно исключить все те числа, которые кратные a2. Это те числа из ряда (1), которые делятся на a2 и не делятся на a1. Числа ряда (1), которые делятся на a2 следующие:
 . . |
Их количество равно 
Эти числа можно представить в виде ka2, где k пробегает натуральные числа
 . . | (3) |
Для того, чтобы ka2 не делился на a1 необходимо и достаточно, чтобы k не делился на a1 (т.к. a1 и a2 взаимно простые числа). Нужно найти количество чисел из ряда (1), которые делятся на a1 и исключить их из ряда (3). 


 . . | (4) |
(4) число тех чисел ряда A1, которые не делятся на a1 или это число тех чисел ряда (1), которые делятся на a2 и не делятся на a1.
Учитывая (2) и (4) получим число тех чисел ряда (1), которые не делятся ни на a1, ни на a2:
  . . | (5) |
Обозначим множество этих чисел через A2. Далее удалим из A2 те числа, которые делятся на a3. Это те числа из ряда (1), которые делятся на a3 и не делятся на a1 и a2.
Числа ряда (1), которые делятся на a3 следующие:
 . . |
Их количество равно 
Эти числа можно представить в виде ka3, где k пробегает натуральные числа
 . . | (6) |
Для того, чтобы ka3 не делился на a1 и a2 необходимо и достаточно, чтобы k не делился на a1 и a2 (т.к. a3 и a1 а также a3 и a2 числа взаимно простые). Нужно найти количество чисел из ряда (1), которые делятся на a1 и a2 и исключить из ряда (6). 

 . . |
Тогда число тех чисел ряда (1), которые не делятся ни на a1, ни на a2, ни на a3:
   . . |
Обозначим множество этих чисел через A3. Рассуждая таким образом, заключим, что число Ai тех чисел ряда (1), которые не делятся на a1, a2, . ai равно
  . . | (7) |
Чтобы найти число тех чисел ряда (1), которые не делятся на a1, a2, . ai+1, нужно из множества (7) исключить числа кратные ai+1. Это те числа ряда (1), которые не делятся на a1, a2, . ai и делятся на ai+1.
Все числа ряда (1), которые делятся на ai+1, следующие:
  , , |
то есть это числа kai+1, где k=1, 2, . m/ai+1 и для того, чтобы kai+1 не делилось на a1, a2, . ai необходимо и достаточно, чтобы k не делилось на a1, a2, . ai. Поэтому из ряда Ai нужно исключить столько чисел, сколько существует в ряду
 |
 |
Если исключить эти числа из ряда Ai, то останутся те числа этого ряда, которые не делятся на числа a1, a2, . ai+1. Их число равно
   |
Мы доказали следующую теорему:
Теорема 1. Если a1, a2, . aq, все различные взаимно простые числа, входящие в m, то число чисел, которые не делятся ни на одно из чисел a1, a2, . aq и входящих в ряд m равно:
  | (8) |
Таким образом справедлива и следующая теорема:
Теорема 2. Если a1, a2, . aq, все различные простые числа, входящие в m, то число чисел, взаимно простых с m и входящих в ряд
| 1, 2, . m |
определяется формулой (8).
Действительно. Всякое число, которое не делится ни на один из простых множителей, входящих в состав m является взаимно простым с m. Тогда учитывая теорему 1, получаем доказательство данной теоремы.
Найденная формула можно переписать и в другом виде. Если a1, a2, a3, . все различные простые числа, входящие множителями в m, то
 |
   |
Рассмотрим численный пример.
Пример. Возьмем число 90. Числа, взаимно простые с 90 и меньше 90 следующие:
| 1, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 49, 53, 59, 61, 67, 71, 73, 77, 79, 83, 89. |
Таких чисел 24. Учитывая, что 90=2·3 2 ·5, для φ(m) мы находим
 |
- Мультипликативность функции Эйлера
- Обобщение функции Эйлера
- Дифференциальное уравнение Эйлера и методы его решения
- Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.
- Решение однородного уравнения Эйлера
- Примеры
- Решение неоднородного уравнения Эйлера
- Пример
- Неоднородное уравнение Эйлера со специальной неоднородной частью
- Решение уравнений с функцией эйлера
- 2.2. Частные случаи уравнений Эйлера
- 2.2.1. Подынтегральная функция F не зависит явно от y‘
- 2.2.2. Подынтегральная функция F линейно зависит от y‘
- 2.2.3. Подынтегральная функция F не зависит явно от y
- 2.2.4. Подынтегральная функция F зависит только от y‘
- 2.2.5. Подынтегральная функция F не зависит явно от x
- 2.3. Вопросы для самопроверки
- 2.4. Примеры выполнения заданий
- 2.4.1. Задание 1
- 2.4.2. Задание 2
- 2.4.3. Задание 3
- 2.5. Задание
- 🔍 Видео
Видео:Функция ЭйлераСкачать

Мультипликативность функции Эйлера
Теорема 3. Если m1 и m2 числа взаимно простые, то
| φ(m1m2)=φ(m1)φ(m2) |
| a1, a2, a3, . b1, b2, b3, . | (9) |
различные простые числа, входящие в состав m1m2, так как m1 и m2 взаимно простые числа, т.е. они не имеют общих делителей.
Справедливо и обратное. Всякое простое число входящее в произведение m1m2 должно совпадать с числом из ряда (9), так как это простое число входит множителем или в m1, или в m2.
Таким образом числа ряда (9) представляют множество всех простых чисел, входящих в произведение m1m2. Следовательно
   |
С другой стороны
  |
  |
| φ(m1m2)=φ(m1)φ(m2). |
| φ(90)=φ(9·10)=φ(9)φ(10), |
  |
| φ(90)=φ(9·10)=φ(9)φ(10)=6·4=24. |
Эта теорема справедлива и для любого числа сомножителей, если эти сомножители взаимно простые числа.
| φ(m1m2m3) = φ(m1)φ(m2m3) = φ(m1)φ(m2)φ(m3). |
| φ(m1m2m3m4) = φ(m1)φ(m2m3m4) = φ(m1)φ(m2)φ(m3)φ(m4). |
| и т.д. |
Видео:233 Мультипликативность функции ЭйлераСкачать

Обобщение функции Эйлера
Как мы уже видели, функция Эйлера φ(m) показывает, сколько в ряду
| 1, 2, . m | (10) |
чисел взаимно простых с m.
Более общая задача состоит в следующем:
Задача 3. Дан ряд (10) и требуется найти число тех чисел, этого ряда, которые имеют с m наибольший общий делитель λ, причем m=nλ, т.е. λ является одним из делителей числа m.
Очевидно, что искомые числа находятся среди чисел
| λ, 2λ , 3λ , . nλ | (11) |
Для того, чтобы λ было наибольшим общим делителем чисел m=nλ и kλ из ряда (11), необходимо и достаточно, чтобы k и n были числами взаимно простыми. Следовательно, т.к. k принимает значения
| 1, 2, . n | (12) |
то искомых чисел столько, сколько найдется чисел из ряда (12) взаимно простых с n. Число таких чисел равно φ(n) (Теорема 2).
Мы доказали следующую теорему:
Теорема 4. Если a1, a2, a3, . все различные простые числа, входящие в m, то число чисел, имеющих с m наибольший общий делитель λ (m=nλ) равен числу
| φ(n)=φ(m/λ) | (12) |
| m=n1λ1=n2λ2=n3λ3=. |
| 1, 2, . m | (13) |
Тогда φ(n1) количество тех чисел, которые с m имеют наибольший общий делитель λ1, φ(n2) количество тех чисел, которые с m имеют наибольший общий делитель λ2, и т.д.
| φ(n1)+φ(n2)+φ(n3)+. =m |
 |
Мы доказали следующую теорему:
Теорема 5. Пусть n1, n2, . nk все делители числа m. Тогда имеет место следующее равенство:
 |
Пример . Пусть m=90. Делители числа m следующие:
Видео:06. Формула ЭйлераСкачать

Дифференциальное уравнение Эйлера и методы его решения
Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.
Видео:Малая теорема Ферма и теорема Эйлера | Ботай со мной #037 | Борис Трушин !Скачать

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.
Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;
;
;
.
Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.
Видео:Функция Эйлера. Мультипликативность и вычислениеСкачать

Решение однородного уравнения Эйлера
Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.
Рассмотрим действительные корни. Пусть ki – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.
Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть ki – кратный корень кратности m . Выразим комплексный корень ki через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.
После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .
Примеры
Видео:Функция Эйлера | Теория чиселСкачать

Решение неоднородного уравнения Эйлера
Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.
Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).
Пример
Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Неоднородное уравнение Эйлера со специальной неоднородной частью
Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.
Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.
Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020
Видео:Остаток от деления 14^245 на 90 | Теорема Эйлера | Теория чисел | КАК РЕШАТЬ?Скачать

Решение уравнений с функцией эйлера
Пример 2.1. Рассмотрим пример, который легко решить аналитически. Требуется найти экстремум функционала
при граничных условиях
Найдём частные производные и
Вычислим полную производную по x от
Составляем дифференциальное уравнение Эйлера вида
или, после упрощений
Его общее решение имеет вид
Для нахождения произвольных постоянных C1 и C2 подставим решение (2.16) в граничные условия (2.11):
Видно, что система (2.17) имеет единственное решение. Решая эту систему, найдём значения C1 и C2:
и тогда уравнение экстремали имеет вид:
Действительно ли на этой кривой достигается экстремум? И если да, то какой: минимум или максимум? Далее, в главе 13, мы рассмотрим достаточные условия экстремума . В частности, мы выведем условие Лежандра: если на экстремали выполняется условие а на функциях, близких к экстремали, для произвольных y‘ имеет место то достигается сильный минимум. В нашем случае это выполняется:
и, следовательно, на нашей экстремали достигается сильный минимум. Проверим этот результат: вычислим на нескольких функциях вида Эти функции удовлетворяют граничным условиям (2.11) и, следовательно, являются допустимыми. Для вычислений применим MATLAB.
Действительно, полученный результат не противоречит выводу о том, что на функции достигается минимум. Но, конечно же, проведенная проверка не доказывает этот факт. Ведь мы проверили только несколько из бесконечного числа функций, графики которых проходят через точки и Доказательством могут служить необходимые и достаточные условия экстремума функционала.
Пример 2.2. Найти экстремаль функционала
при граничных условиях
Выводим уравнение Эйлера вида (2.9). Частные производные:
Уравнение Эйлера после упрощений имеет вид:
Его общее решение
Находим произвольные постоянные из граничных условий (3.22). Подставляем решение (3.25) в эти граничные условия:
Мы видим, что из полученной системы уравнений можно найти только а C2 может быть произвольной. Поэтому данная вариационная задача имеет бесчисленное множество решений вида
На любой из этих функций функционал принимает постоянное значение (какое − мы сейчас посчитаем). Проверка по достаточному условию Лежандра даёт:
поэтому на экстремалях (3.27) достигается сильный минимум.
Посчитаем значение функционала (2.21) на функциях вида (2.27) и нарисуем несколько экстремалей с помощью MATLAB.
На каждой из наших функций функционал равен нулю.
Видео:Теория чисел. 6. Методы решения сравнений 1 й степениСкачать

2.2. Частные случаи уравнений Эйлера
Иногда решение уравнения Эйлера существенно упрощается. Рассмотрим соответствующие частные случаи.
2.2.1. Подынтегральная функция F не зависит явно от y‘
Материал этого подраздела изложен в книге.
2.2.2. Подынтегральная функция F линейно зависит от y‘
Материал этого подраздела изложен в книге.
2.2.3. Подынтегральная функция F не зависит явно от y
Материал этого подраздела изложен в книге.
2.2.4. Подынтегральная функция F зависит только от y‘
Материал этого подраздела изложен в книге.
2.2.5. Подынтегральная функция F не зависит явно от x
Материал этого подраздела изложен в книге.
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

2.3. Вопросы для самопроверки
- Какую вариационную задачу мы решаем?
- Как выводится дифференциальное уравнение Эйлера?
- Где используется в выводе дифференциального уравнения Эйлера основная лемма вариационного исчисления?
- Почему обращается в нуль внеинтегральное слагаемое в формуле (2.8) при интегрировании по частям?
- Чем отличается частная производная от полной?
- Какие Вы знаете методы решения дифференциальных уравнений порядка?
- Всегда ли решение вариационной задачи будет единственным? От чего это зависит?
- Какие частные случаи уравнения Эйлера Вы знаете?
- В каких случаях уравнение Эйлера перестаёт быть дифференциальным и становится конечным?
- В каких случаях вариационная задача теряет смысл?
- Как записывается интеграл уравнения Эйлера, если подынтегральная функция F не зависит явно от y?
- Каким будет решение уравнения Эйлера, если подынтегральная функция F зависит только от y‘?
- Как решается уравнение Эйлера, если подынтегральная функция F не зависит явно от y‘?
- Как решается задача о брахистохроне?
Видео:17. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами Ч2Скачать

2.4. Примеры выполнения заданий
2.4.1. Задание 1
Найти экстремаль функционала
Исследовать полученную экстремаль на достаточные условия экстремума. Вычислить значение функционала на найденной экстремали и, для сравнения, на прямой, соединяющей точки и Построить график решения.
В этом примере подынтегральная функция является функцией общего вида, поэтому составим уравнение Эйлера в виде (2.9) и решим его. Затем построим график решения. Попутно исследуем на выполнение достаточных условий экстремума и вычислим значение функционала на экстремали и отрезке прямой M1M2. Применим для решения задачи MATLAB.
Очистим память. Напечатаем заголовок решаемой задачи. Если хотите, задайте другую строку для вывода (например, свою фамилию). Опишем символические переменные [58]. Для решения уравнения Эйлера используем принятые в MATLAB обозначения производных: Dy для y‘ и D2y для y». Аргумент обозначим x , а функцию − y .
Вводим подынтегральную функцию и граничные условия. Печатаем их. Здесь вы должны поставить свои исходные данные: подынтегральную функцию F и граничные условия x1, y1, x2, y2.
Начинаем вывод дифференциального уравнения Эйлера (2.9). Найдём частные производные Fy и Fy’. Напечатаем их.
В уравнение Эйлера (2.9) входит полная производная Вычислим её по обычной формуле дифференцирования сложной функции:
Напечатаем её. Напечатаем также величину необходимую для проверки достаточных условий экстремума по признаку Лежандра.
Составим левую часть дифференциального уравнения Эйлера (2.9) и упростим её. Преобразуем символическую переменную Euler в строку.
Мы составили уравнение Эйлера, теперь решим его. Команда dsolve позволяет находить как общее решение дифференциального уравнения, так и частное его решение, удовлетворяющее заданным начальным или граничным условиям. В следующих главах при решении других заданий нам нужно будет иметь общее решение уравнения Эйлера. Найдём его.
Сформируем теперь уравнения для граничных условий. Подставим в найденное аналитическое решение Sol граничные точки x1 и x2 , и приравняем их соответственно y1 и y2 .
Решаем полученную систему конечных уравнений − находим значения произвольных постоянных C1 и C2 . Присваиваем найденные решения символическим константам, полученным при решении дифференциального уравнения. Теперь вычисляем аналитическое решение Sol21 . Такое вычисление сводится к тому, что в него будут подставлены найденные значения констант C1 и C2 . Печатаем найденное уравнение экстремали.
Вычислим значения функционала (2.86) на найденной экстремали и на прямой, соединяющей точки M1 и M2. Подставим в подынтегральную функцию F аналитические выражения для этих линий и их производных, а затем проинтегрируем. Напечатаем результаты.
В данном примере условие Лежандра говорит о сильном минимуме, что подтверждается полученным результатом: значение функционала на экстремали меньше, чем на другой допустимой функции. А как в вашем варианте: какой экстремум достигается? И подтверждается ли этот результат сравнением величин Jextr и Jlin ? Если нет, то не забудьте, что найденный экстремум − только локальный, а не глобальный! Попробуйте вычислить значение функционала не на прямой M1M2, а на какой-нибудь другой допустимой кривой, достаточно близкой к экстремали. Например, можно наложить на экстремаль несколько полуволн синусоиды, смещённой и деформированной вдоль оси Ox так, что
И, наконец, строим график. Задаём массив аргументов для рисования графика функции и вычисляем значения функции. Рисуем график, подписываем заголовок и координатные оси установленным шрифтом.
2.4.2. Задание 2
Найти экстремаль функционала
Исследовать на выполнение достаточных условий экстремума. Построить график решения.
В этом примере подынтегральная функция не зависит явно от y. Первый интеграл уравнения Эйлера имеет вид (2.43). Составим программу для решения этой вариационной задачи. Вначале введём исходные данные. У нас будет первый интеграл уравнения Эйлера, поэтому ни сама функция y, ни её вторая производная y» нам не нужны, и мы их не описываем. Поставьте свою подынтегральную функцию и граничные условия.
Строим первый интеграл и решаем полученное дифференциальное уравнение. Названия констант C1 и C2 используются в команде dsolve , поэтому при составлении интеграла уравнения Эйлера обозначим константу C . Все использованные здесь функции и операторы MATLAB были описаны ранее, в примере 1.
В переменной Sol получено общее решение, произвольные постоянные обозначены C и C1 . Найдём их. Для этого подставим в Sol граничные точки. Приравняем полученные выражения соответственно y1 и y2 . Тем самым мы сформируем систему уравнений.
Решим полученную систему − найдём произвольные постоянные C и C1 . Подставим их в решение Sol . Ограничим решение 14 знаками. Напечатаем уравнение найденной экстремали.
Дальнейшие действия не отличаются от описанных в примере 1. Рисуем график и и вычисляем Fy’y’, которая нужна для проверки достаточных условий экстремума по признаку Лежандра.
Проанализируйте достаточное условие Лежандра. Достигается ли экстремум на вашей экстремали? Если да, то какой?
2.4.3. Задание 3
Решить задачу о брахистохроне, соединяющей точки и
Мы уже решили эту задачу аналитически. Нам осталось найти значение константы C1 и параметра в конечной точке t2 из решения системы уравнений (2.84). Составим программу для решения этого примера. Вначале введём исходные данные задачи. Подставьте свою правую точку.
Составляем систему уравнений (2.84). Левую часть каждого уравнения мы задаём сразу в виде строки. В правой части переводим числа x2 и y2 в их строковые представления с помощью функции num2str . Ранее мы использовали конструкцию char(sym(y2)) . Оба варианта работают правильно − вы можете это проверить. Решаем полученную систему уравнений аналитически. Печатаем решения.
Рисуем график полученной брахистохроны. Выбираем начало координат в левом верхнем углу с помощью команды axis . Задаём границы по оси Ox, чтобы график занимал всё место на рисунке. Выравниваем масштабы по осям координат, чтобы брахистохрона выглядела неискажённой. Надписываем заголовок и метки осей.
Видео:Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

2.5. Задание
Для своего варианта функционалов 1, 2, 3 найти экстремали, построить их графики и исследовать на выполнение достаточных условий экстремума.
🔍 Видео
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

7 Функция ЭйлераСкачать

Метод ЭйлераСкачать

Дифференциальное уравнение. Формула ЭйлераСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0Скачать