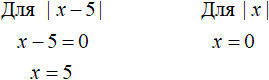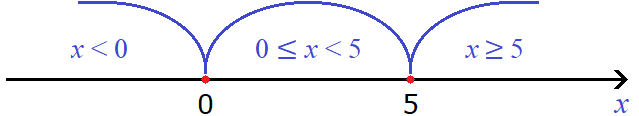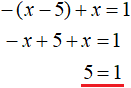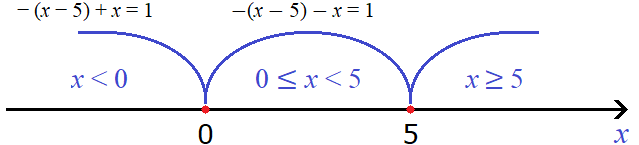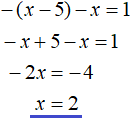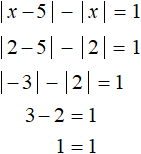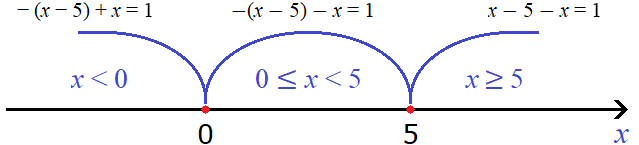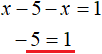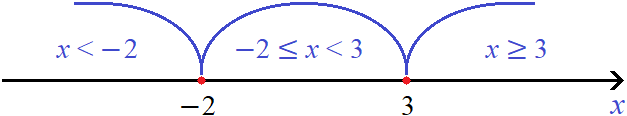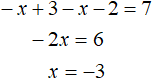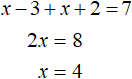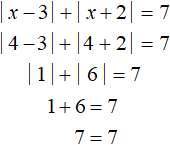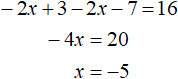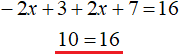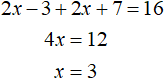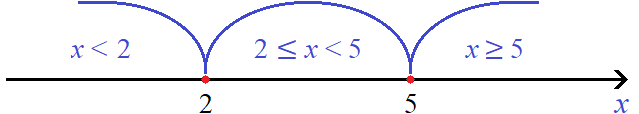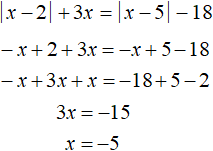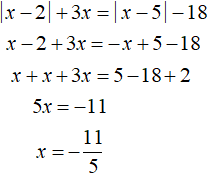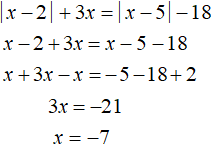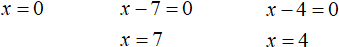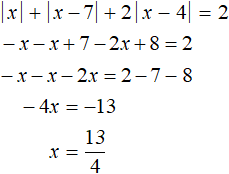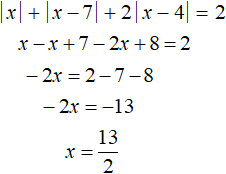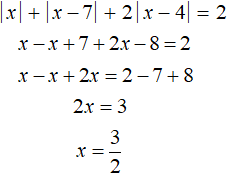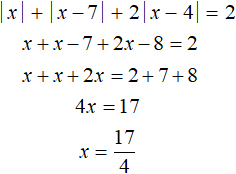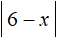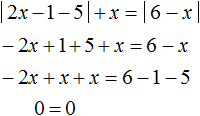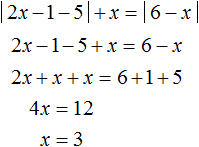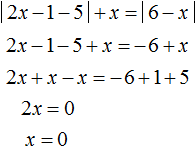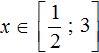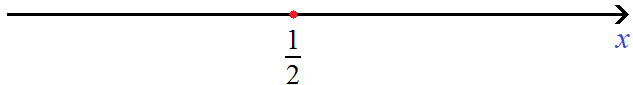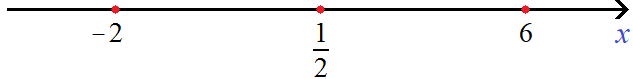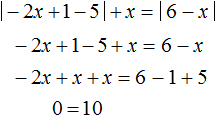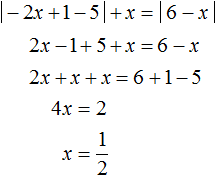Решение уравнений с двумя модулями 10 класс

Видео:Уравнения с модулемСкачать

Уравнения с несколькими модулями в одной части

Чем больше модулей, тем больше приходиться их раскрывать и тем больше получается различных уравнений. Когда модулей один или два — это не сложно. Сложность возникает когда модулей больше двух. Человек может забыть рассмотреть какой-то из случаев, и получится что уравнение решено не полностью.

Давайте решим следующее уравнение:

У данного уравнения два модуля в левой части. Оно решается путем раскрытия модулей. Не будем комментировать решение, а сразу приведём его:

Такой вид уравнения удобнее решать методом интервалов (или более точно — методом промежутков). Суть этого метода в том, чтобы разбить координатную прямую на несколько промежутков, а затем решить уравнение на каждом из этих промежутков. Модули исходного уравнения на каждом промежутке будут раскрываться по разному.

Решим уравнение |x − 5| − |x| = 1 методом интервалов.

Для начала нарисуем координатную прямую и обозначим её как x

Если координатная прямая содержит все числа, которые существуют в природе, то логично что она содержит и корни нашего уравнения.

Теперь надо разбить координатную прямую на промежутки. Для этого сначала нужно найти на ней те точки, на которых модули нашего уравнения будут менять свой порядок раскрытия. То есть, найти точки перехода для модулей |x − 5| и |x| .

Чтобы найти точки перехода, нужно выяснить при каких значениях x подмодульные выражения равны нулю. Узнать это можно приравняв к нулю подмодульные выражения обоих модулей, и решить обычные линейные уравнения:

Для модуля |x − 5| точкой перехода будет 5 . Для модуля |x| точкой перехода будет 0 .

Теперь отметим точки перехода на координатной прямой. Мéньшие числа нужно отмечать левее, большие числа правее:

Проведем дуги от точек перехода:

С помощью неравенств подпишем каждый промежуток. Получится три промежутка: от минус бесконечности до нуля, от нуля до пяти, и от пяти до плюс бесконечности. То есть: x x значение 0 не включено в данный промежуток. Но зато это значение включено во второй промежуток 0 ≤ x .

Во втором же промежутке 0 ≤ x значение 5 не включено в данный промежуток, но зато оно включено в третий промежуток x ≥ 5 .

Проще говоря, каждый промежуток включает в себя левый конец, и не включает правый. Сделано это специально, чтобы не допустить потерь значений переменной x. Описать с помощью неравенств нужно все значения на координатной прямой, не допуская их потерь.

Включение левого конца в рассматриваемый промежуток и исключение его из правого это лишь общепринятое правило. На самом деле концы рассматриваемого промежутка можно включать в любой из соседствующих промежутков. Например, значение 0 можно было включить в первый промежуток. Тогда он принял бы вид x ≤ 0 , а второй промежуток принял бы вид 0 , потому что ноль уже был включен в первый промежуток.

Но лучше всего исходить из ситуации, потому что в каких-то случаях левый конец промежутка целесообразнее исключить из рассматриваемого промежутка и включить его в правый конец соседнего промежутка. Об этом мы поговорим позже.

Теперь выясним как будут вести себя модули |x − 5| и |x| на каждом из этих промежутков. От этого будет зависеть то, как они будут раскрываться.

Начнем с первого промежутка x x , то при любом значении x на данном промежутке подмодульное выражение x − 5 станет отрицательным, а значит модуль |x − 5| на промежутке x −(x − 5) + x = 1 , которое получилось после раскрытия модулей на промежутке x

Это уравнение решений не имеет. Значит на промежутке x исходное уравнение не имеет корней. Проще говоря, корень уравнения не является числом меньшим нуля.

Следующий промежуток, на котором нужно решить уравнение это промежуток 0 ≤ x .

Если x больше или равно нулю, но меньше пяти, то подмодульное выражение x − 5, станет отрицательным, а значит модуль |x − 5| на промежутке 0 ≤ x будет раскрываться со знаком минус. Второй модуль |x| на промежутке 0 ≤ x будет раскрываться с плюсом.

В результате после раскрытия модулей на промежутке 0 ≤ x уравнение с модулем |x − 5| − |x| = 1 примет вид −(x − 5) − x = 1

Решим это уравнение:

Получили корень 2. Чтобы проверить действительно ли это число является корнем исходного уравнения, нужно посмотреть принадлежит ли это число рассматриваемому промежутку 0 ≤ x . Принадлежит? Да. Значит число 2 является корнем уравнения |x − 5| − |x| = 1 . Проверка также показывает это:

Следующий промежуток, который нужно рассмотреть это промежуток x ≥ 5 .

Если x больше или равно пяти, то модуль |x − 5| на промежутке x ≥ 5 будет раскрываться со знаком плюс. Второй модуль |x| на промежутке x ≥ 5 тоже будет раскрываться с плюсом.

В результате после раскрытия модулей на промежутке x ≥ 5 уравнение с модулем |x − 5| − |x| = 1 примет вид x − 5 − x = 1 .

Решим это уравнение:

Это уравнение не имеет решений. Значит на промежутке x ≥ 5 исходное уравнение корней не имеет. Проще говоря, корень уравнения не является числом, бóльшим либо равным пяти.

В итоге корнем уравнения является число 2, которое мы нашли решив исходное уравнение на промежутке 0 ≤ x

Пример 2. Решить уравнение |x − 3| + |x + 2| = 7

Решение

Шаг 1. Находим точки перехода для модулей |x − 3| и |x + 2|

Шаг 2. Отметим на координатной прямой найденные точки перехода и выделим получившиеся промежутки:

Шаг 3. Решим исходное уравнение на каждом промежутке. Для этого посмóтрим как будут раскрываться модули |x − 3| и |x + 2| на этих промежутках.

На промежутке x модуль |x − 3| будет раскрываться с минусом. Можно проверить это, подставив в данный модуль любое число из промежутка x . Например, числа −4 или −9

Следующий модуль |x + 2| на промежутке x тоже будет раскрываться с минусом. Убедимся в этом подставив любые два числа из промежутка x в подмодульное выражение. Например, числа −6 и −8

Значит после раскрытия модулей на промежутке x исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:

Обязательно нужно проверить входит ли найденный корень −3 в рассматриваемый промежуток x x найденный корень −3 и проверить верное ли оно. В данном случае неравенство −3 верно, значит корень −3 входит в промежуток x и соответственно является корнем исходного уравнения.

На следующем промежутке −2 ≤ x x ≥ 3 исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:

Решим это уравнение:

Этот корень входит в рассматриваемый промежуток x ≥ 3, значит является корнем исходного уравнения. Проверка также показывает это:

Ответ: −3 и 4.

Пример 3. Решить уравнение |2x − 3| + |2x + 7| = 16

Решение

Найдём точки перехода для модулей |2x − 3| и |2x + 7|

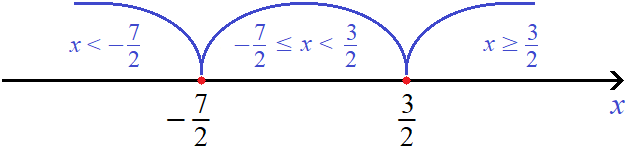
Отметим точки перехода на координатной прямой. Меньшие числа нужно отмечать левее, большие правее:

Решим исходное уравнение |2x − 3| + |2x + 7| = 16 на промежутке 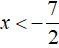. Оба модуля на этом промежутке будут раскрываться с минусом:

Корень −5 принадлежит промежутку 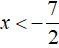, значит является корнем исходного уравнения.

Теперь решим исходное уравнение на промежутке 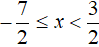. Модуль |2x − 3| на этом промежутке раскрывается с минусом, а модуль |2x + 7| — с плюсом:

Видим, что на промежутке исходное уравнение не имеет решений (корней).

Теперь решим исходное уравнение на промежутке 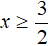. Оба модуля на данном промежутке раскрываются с плюсом:

Корень 3 принадлежит промежутку 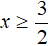, значит является корнем исходного уравнения.

Ответ: −5 и 3 .

Пример 4. Решить уравнение |x − 2| + 3x = |x − 5| − 18

Решение

Найдём точки перехода для модулей |x − 2| и |x − 5|

Отметим точки перехода на координатной прямой:

Решим исходное уравнение на промежутке x . Модули |x − 2| и |x − 5| на этом промежутке раскрываются с минусом:

Число −5 принадлежит промежутку x , значит является корнем исходного уравнения.

Решим исходное уравнение на промежутке 2 ≤ x . Модуль |x − 2| на этом промежутке раскрывается с плюсом, а модуль |x − 5| — с минусом:

Число 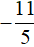не принадлежит промежутку 2 ≤ x , значит не является корнем исходного уравнения.

Решим исходное уравнение на промежутке x ≥ 5 . Модули |x − 2| и |x − 5| на этом промежутке будут раскрываться с плюсом:

Число −7 не принадлежит промежутку x ≥ 5 , значит не является корнем исходного уравнения.

Ответ: −5

Пример 5. Решить уравнение |x| + |x − 7| + 2|x − 4| = 2

Решение

Найдём точки перехода для модулей |x|, |x − 7| и |x − 4|

Отметим точки перехода на координатной прямой:

Решим исходное уравнение на промежутке x . Все три модуля: |x|, |x − 7| и |x − 4| на этом промежутке раскрываются с минусом:

Число 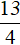не принадлежит промежутку x , значит не является корнем исходного уравнения.

Решим теперь исходное уравнение на промежутке 0 ≤ x |x| на этом промежутке раскрывается с плюсом, а модули |x − 7| и |x − 4| — с минусом:

Число 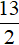не принадлежит промежутку 0 ≤ x , значит не является корнем исходного уравнения.

Решим теперь исходное уравнение на промежутке 4 ≤ x . Модуль |x| на этом промежутке раскрывается с плюсом; модуль |x − 7| — с минусом; модуль |x − 4| — с плюсом:

Число не принадлежит промежутку 4 ≤ x , значит не является корнем исходного уравнения.

Решим исходное уравнение на промежутке x ≥ 7 . Все три модуля: |x|, |x − 7| и |x − 4| на этом промежутке раскрываются с плюсом:

Число 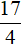не принадлежит промежутку x ≥ 7 , значит не является корнем исходного уравнения.

Решив исходное уравнение на каждом промежутке, мы не нашли корней, удовлетворяющих этому уравнению. Значит данное уравнение не имеет корней.

В ответе можно написать словами, что корней нет (или решений нет), либо указать символ пустого множества. Этот символ будет указывать, что множество корней уравнения |x| + |x − 7| + 2|x − 4| = 2 пусто.

Ответ: ø.

Пример 6. Решить уравнение

Решение

Найдём точки перехода для модулей 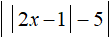и

Если методом интервалов нужно решить уравнение с модулем, который в свою очередь содержит внутри себя другой модуль, то точки перехода надо искать для случаев: когда внутренний модуль раскрывается с плюсом и когда он раскрывается с минусом. Точки перехода будут меняться в зависимости от этих случаев. Давайте посмотрим как это происходит.

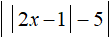
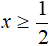
Если у модуля внутренний модуль раскроется с плюсом, то есть если 2x − 1 ≥ 0 (что равносильно ), то исходное уравнение примет вид |2x − 1 − 5| + x = |6 − x| . Здесь и далее надо учесть, что внутренний модуль будет раскрываться с плюсом при тех значениях x, которые будут больше либо равны . Отметим эту точку на координатной прямой.

Теперь найдем точки перехода. Поскольку исходное уравнение приняло вид |2x − 1 − 5| + x = |6 − x| , то точки перехода надо найти для модулей |2x − 1 − 5| и |6 − x| .

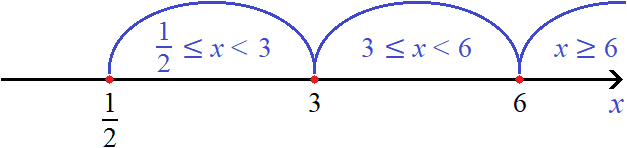
Для модуля |2x − 1 − 5| точкой перехода будет число 3 , а для модуля |6 − x| — число 6 . Отметим эти числа на той же координатной прямой где мы отметили точку

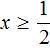
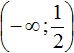
Сейчас нас интересуют только те значения x , которые удовлетворяют условию , потому что только при этом условии внутренний модуль исходного уравнения раскрывается с плюсом. Поэтому рассматривать промежуток мы не будем. Рассмотреть нужно те промежутки где x удовлетворяет условию

Первый промежуток на котором мы будем решать уравнение это 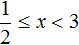. На нем модуль |2x − 1 − 5| раскрывается с минусом, а модуль |6 − x| с плюсом:

Получили тождество — равенство верное при любом значении x . В данном случае решением исходного уравнения является любое число из промежутка . Любое число из этого промежутка 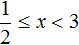также удовлетворяют условию

Теперь решим исходное уравнение на промежутке 3 ≤ x . Оба модуля на этом промежутке раскрываются с плюсом. Тогда:

Корень 3 принадлежит рассматриваемому промежутку. Также этот корень удовлетворяет условию 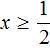, согласно которому внутренний модуль исходного уравнения раскрывается с плюсом.

Теперь решим исходное уравнение на промежутке x ≥ 6 . На этом промежутке модуль |2x − 1 − 5| раскрывается с плюсом, а модуль |6 − x| с минусом. Тогда:

Корень 0 не удовлетворяет условию x ≥ 6 , значит на данном промежутке исходное уравнение корней не имеет.

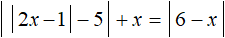
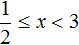
Итак, если внутренний модуль уравнения раскрывается с плюсом, то решениями уравнения являются: промежуток , а также число 3. Запишем эти решения одним промежутком:

Теперь решим исходное уравнение для случая когда внутренний модуль раскрывается с минусом. То есть когда 2x − 1 (что равносильно неравенству 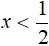). В этом случае исходное уравнение примет вид:

Отметим точку на координатной прямой.

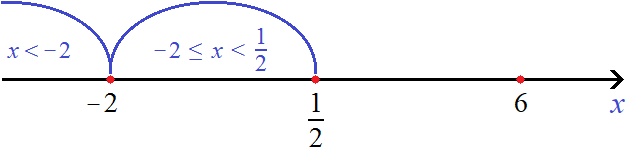
Нас будут интересовать те значения x которые располагаются слева от . Это те значения при которых внутренний модуль исходного уравнения раскрывается с минусом.

Найдем точки перехода для модулей |−2x + 1 − 5| и |6 − x| . Для первого модуля это число −2, для второго модуля — число 6

Рассматривать будем только те промежутки, которые располагаются слева от . Только при них внутренний модуль исходного уравнения раскрывается с минусом

Решим уравнение на промежутке x . На этом промежутке оба модуля раскрываются с плюсом. Тогда:

Это уравнение решений не имеет. Значит на промежутке x исходное уравнение не имеет корней.

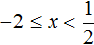
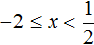
Решим теперь уравнение на промежутке . Замечаем, что при подстановке левого конца этого промежутка (числа −2) в модуль |−2x + 1 − 5| данный модуль раскрывается с плюсом, а при остальных значениях промежутка модуль |−2x + 1 − 5| раскрывается с минусом.

Поэтому число −2 разумнее включить в промежуток x , который мы уже рассмотрели. На промежутке x модуль раскрывался с плюсом, и при включении числа −2 в данный промежуток, он также будет раскрываться с плюсом.

На промежутке 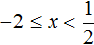модуль |−2x + 1 − 5| раскрывается с минусом, а модуль |6 − x| с плюсом. Тогда:

Получится корень который не удовлетворяет условию 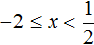. Несмотря на это число является корнем исходного уравнения, потому что мы получили его когда решали уравнение для случая 2x − 1 ≥ 0 .

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Задания для самостоятельного решения

Примечание: Решения, не удовлетворяющие исходному уравнению, подчёркнуты красным.

Видео:Контрольная работа. Уравнения с МОДУЛЕМСкачать

Уравнения с двумя модулями

До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида |f(x)|=g(x)

Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:

Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.

Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:

Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.

Давайте попробуем решать вот такую задачу:

Элементарно, Ватсон! Раскрываем модули:

Рассмотрим отдельно каждый случай:

В первом уравнении корней нет. Потому что когда это 3=−7

? При каких значениях x? «Какой ещё нафиг x? Ты обкурился? Там вообще нет x» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной x

, и при этом само равенство — неверное. Потому и нет корней.:)

Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:

Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)

В итоге окончательный ответ: x=1

Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:

. Поэтому сразу переписываем его, раскрывая знак модуля:

Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:

Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.

Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:

Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)

В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:

Первое уравнение имеет корни x=3

. Второе вообще является точным квадратом:

Поэтому у него единственный корень: x=1

. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:

Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)

Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:

(т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:

Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:

Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:

Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)

Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)

Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.

Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.

Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких x

сумма двух модулей равна нулю.:)

В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:

Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:

А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:

Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: x=1

Видео:Уравнения с модулем. Часть 2 | Математика | TutorOnlineСкачать

Уравнения с модулем

Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.

Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.

Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.

Прежде всего вспомним, что

Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)

Видео:11 класс, 29 урок, Уравнения и неравенства с модулямиСкачать

Слева модуль, справа число

Это самый простой случай. Решим уравнение

Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:

Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.

Видео:Уравнение с двумя модулями: особенности решенияСкачать

Переменная как под модулем, так и вне модуля

Здесь приходится раскрывать модуль по определению. . . или соображать!

Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:

Решение первой системы: . У второй системы решений нет.
Ответ: 1.

Первый случай: x ≥ 3. Снимаем модуль:

Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.

Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:

Значит, больше трёх и потому является корнем исходного уравнения

Стало быть, годятся лишь и .

Ответ:

Видео:УРАВНЕНИЯ С МОДУЛЕМ | метод интерваловСкачать

Квадратные уравнения с заменой |x| = t

Поскольку , удобно сделать замену |x| = t. Получаем:

Видео:Неравенства с модулем | Математика | TutorOnlineСкачать

Модуль равен модулю

Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:

Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:

Остаётся решить каждое из уравнений совокупности и записать ответ.

Видео:Уравнение с двумя модулями #1Скачать

Два или несколько модулей

Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.

Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)

Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.

Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:

Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.

Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:

Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.

Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:

Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.

Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:

Ничего нового. Мы и так знаем, что x = 1 является решением.

Видео:Решение уравнения с модулем |x+8|+|x-3|+|x+2|=1.Скачать

Модуль в модуле

Начинаем с раскрытия внутреннего модуля.

1) x ≤ 3. Получаем:

Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.

1.1) Получаем в этом случае:

Это значение x не годится, так как не принадлежит рассматриваемому промежутку.

1.2) . Тогда:

Это значение x также не годится.

Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.

Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:

Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.

Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.

Читайте также о том, как решать неравенства с модулем.

🎬 Видео

Попробуй решить. Уравнения с модулями. Математика 10-11 классы.Скачать

Уравнение с двумя модулями - bezbotvyСкачать

МодульСкачать

Уравнение с двумя модулями #3Скачать

Уравнения с модулямиСкачать

Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Как решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать

УРАВНЕНИЯ С МОДУЛЕМ. Метод интервалов для решения уравнений.Скачать

10 класс, 5 урок, Модуль действительного числаСкачать

НЕРАВЕНСТВА С МОДУЛЕМ 😉 ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать