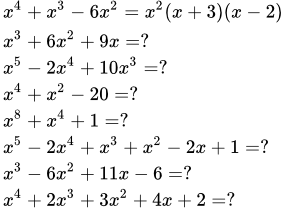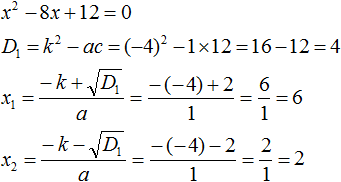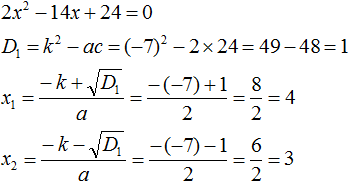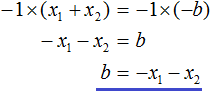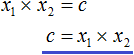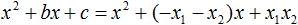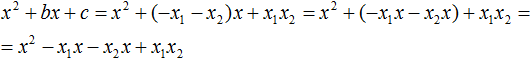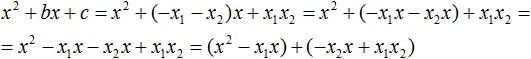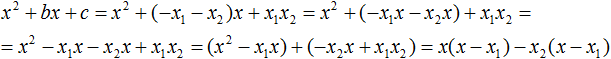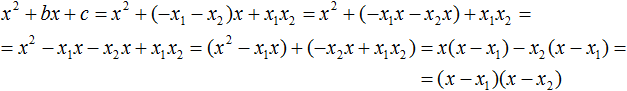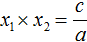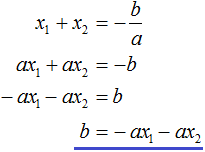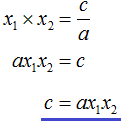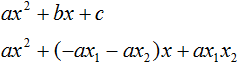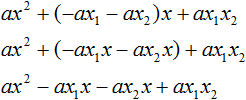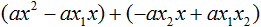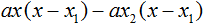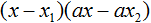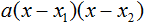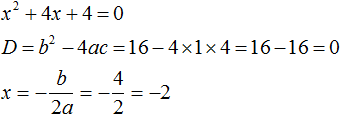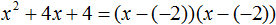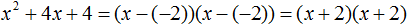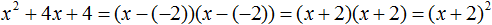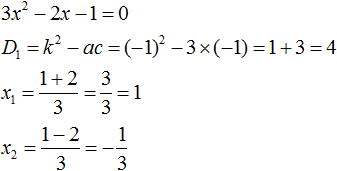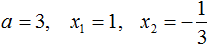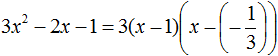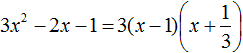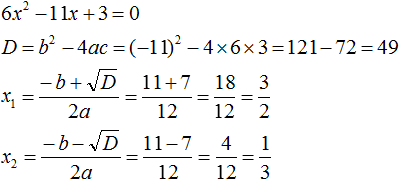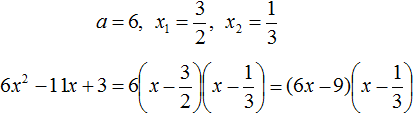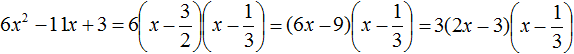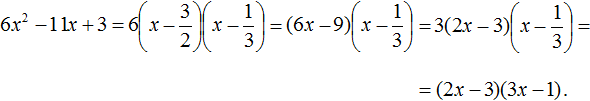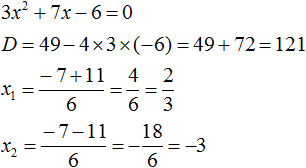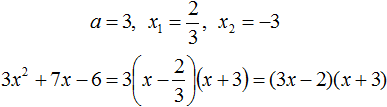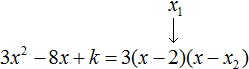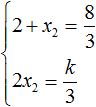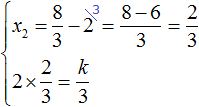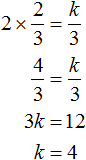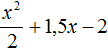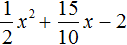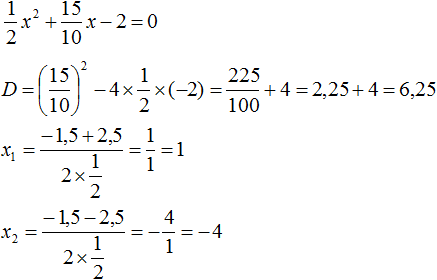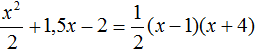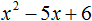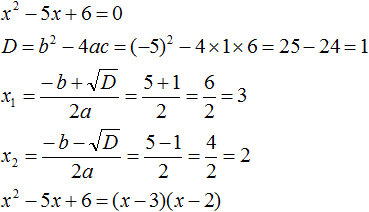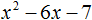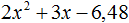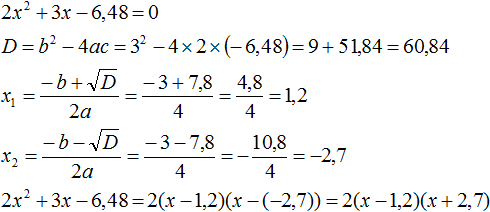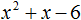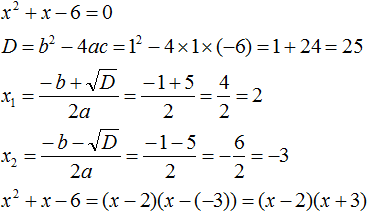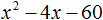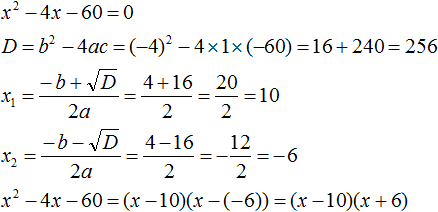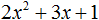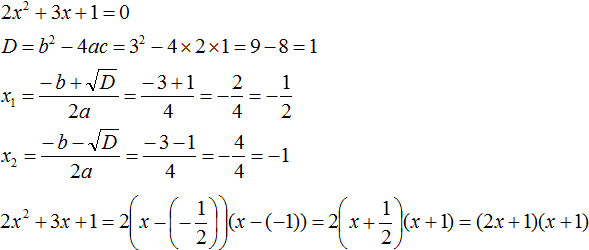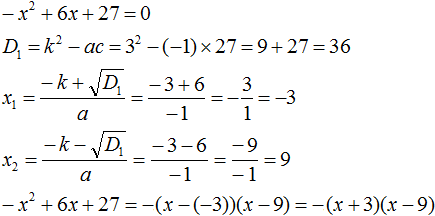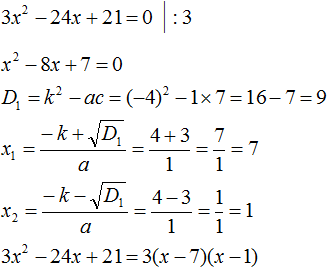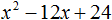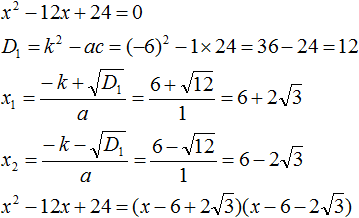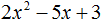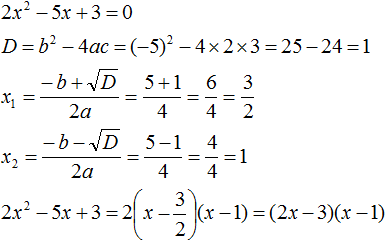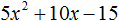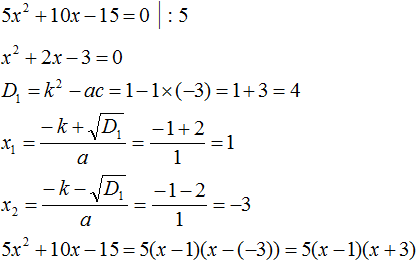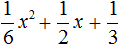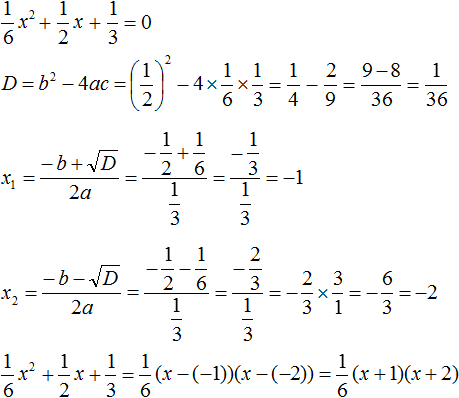Решение уравнений разложением на множители примеры

Решение уравнений разложения на множители (метод расщепления) – это способ решения уравнений при котором мы стремимся уравнение свести их к виду:

а затем каждую скобку приравнять к нулю и решить как отдельное уравнение.

Вынесем за скобку икс.

Разобьем уравнение на два простейших.

В первом корень уравнения уже понятен, во втором надо перенести (5) в правую сторону.

Решение методом разложения на множители основывается на простой идее:

В результате умножения ноль можно получить, только если один из множителей равен нулю.

Попробуйте придумать два числа, которые при умножении дают ноль. Вы убедитесь, что хотя бы одно из них обязательно должно быть нулем.

Этот метод решения уравнений один из самых популярных, поэтому освоить его очень важно для тех, кто планирует иметь четверки и пятерки. А для освоения этого метода, конечно, надо уметь раскладывать на множители как Бог: знать все формулы сокращенного умножения, легко выносить множители за скобки, уметь применять метод группировки и т.д. Подробнее о всех способах разложения на множители смотри здесь .

Пример(задание из ОГЭ). Решите уравнение (x^3+4x^2-4x-16=0).
Решение:

Перед нами кубическое уравнение.
Применим метод группировки: из первой пары слагаемых вынесем (x^2), а из второй – минус четверку.

Видео:Алгебра 10 класс (Урок№12 - Решение алгебраических уравнений разложением на множители.)Скачать

Примеры разложения многочленов на множители

Видео:РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ / Алгебра 7 классСкачать

Примеры с решением квадратного уравнения

Пример 1.1

Разложить многочлен на множители:
x 4 + x 3 – 6 x 2 .

Выносим x 2 за скобки:
.
Решаем квадратное уравнение x 2 + x – 6 = 0 :
.
Корни уравнения:
, .

Отсюда получаем разложение многочлена на множители:
.

Пример 1.2

Разложить на множители многочлен третьей степени:
x 3 + 6 x 2 + 9 x .

Выносим x за скобки:
.
Решаем квадратное уравнение x 2 + 6 x + 9 = 0 :
Его дискриминант: .
Поскольку дискриминант равен нулю, то корни уравнения кратные: ;
.

Отсюда получаем разложение многочлена на множители:
.

Пример 1.3

Разложить на множители многочлен пятой степени:
x 5 – 2 x 4 + 10 x 3 .

Выносим x 3 за скобки:
.
Решаем квадратное уравнение x 2 – 2 x + 10 = 0 .
Его дискриминант: .
Поскольку дискриминант меньше нуля, то корни уравнения комплексные: ;
, .

Разложение многочлена на множители имеет вид:
.

Если нас интересует разложение на множители с действительными коэффициентами, то:
.

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Примеры разложения многочленов на множители с помощью формул

Примеры с биквадратными многочленами

Пример 2.1

Разложить биквадратный многочлен на множители:
x 4 + x 2 – 20 .

Применим формулы:
a 2 + 2 ab + b 2 = ( a + b ) 2 ;
a 2 – b 2 = ( a – b )( a + b ) .

;
.

Пример 2.2

Разложить на множители многочлен, сводящийся к биквадратному:
x 8 + x 4 + 1 .

Применим формулы:
a 2 + 2 ab + b 2 = ( a + b ) 2 ;
a 2 – b 2 = ( a – b )( a + b ) :

;

;
.

Пример 2.3 с возвратным многочленом

Разложить на множители возвратный многочлен:
.

Возвратный многочлен имеет нечетную степень. Поэтому он имеет корень x = – 1 . Делим многочлен на x – (–1) = x + 1 . В результате получаем:
.
Делаем подстановку:
, ;
;

;
.

Видео:Решение уравнений с помощью разложения на множители | Алгебра 7 класс #23 | ИнфоурокСкачать

Примеры разложения многочленов на множители с целыми корнями

Пример 3.1

Разложить многочлен на множители:
.

Предположим, что уравнение

имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x ). То есть целый корень может быть одним из чисел:
–6, –3, –2, –1, 1, 2, 3, 6 .
Подставляем поочередно эти значения:
(–6) 3 – 6·(–6) 2 + 11·(–6) – 6 = –504 ;
(–3) 3 – 6·(–3) 2 + 11·(–3) – 6 = –120 ;
(–2) 3 – 6·(–2) 2 + 11·(–2) – 6 = –60 ;
(–1) 3 – 6·(–1) 2 + 11·(–1) – 6 = –24 ;
1 3 – 6·1 2 + 11·1 – 6 = 0 ;
2 3 – 6·2 2 + 11·2 – 6 = 0 ;
3 3 – 6·3 2 + 11·3 – 6 = 0 ;
6 3 – 6·6 2 + 11·6 – 6 = 60 .

Итак, мы нашли три корня:
x ₁ = 1 , x ₂ = 2 , x ₃ = 3 .
Поскольку исходный многочлен – третьей степени, то он имеет не более трех корней. Поскольку мы нашли три корня, то они простые. Тогда
.

Пример 3.2

Разложить многочлен на множители:
.

Предположим, что уравнение

имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x ). То есть целый корень может быть одним из чисел:
–2, –1, 1, 2 .
Подставляем поочередно эти значения:
(–2) 4 + 2·(–2) 3 + 3·(–2) 3 + 4·(–2) + 2 = 6 ;
(–1) 4 + 2·(–1) 3 + 3·(–1) 3 + 4·(–1) + 2 = 0 ;
1 4 + 2·1 3 + 3·1 3 + 4·1 + 2 = 12 ;
2 4 + 2·2 3 + 3·2 3 + 4·2 + 2 = 54 .

Итак, мы нашли один корень:
x ₁ = –1 .
Делим многочлен на x – x ₁ = x – (–1) = x + 1 :

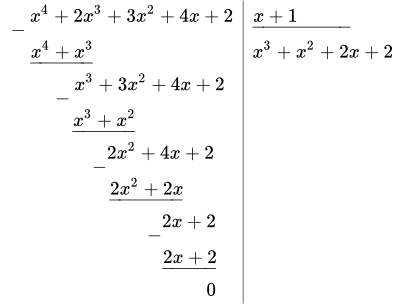
Тогда,
.

Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x ). То есть целый корень может быть одним из чисел:
1, 2, –1, –2 .
Подставим x = –1 :
.

Итак, мы нашли еще один корень x ₂ = –1 . Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.

Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то разложение многочлена на множители имеет вид:
.

Автор: Олег Одинцов . Опубликовано: 18-06-2015

Видео:РЕШЕНИЕ УРАВНЕНИЯ С ПОМОЩЬЮ РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ. Примеры | АЛГЕБРА 7 классСкачать

Разложение квадратного трёхчлена на множители

Видео:Разложение кубических выражений на множителиСкачать

Как разложить на множители квадратный трёхчлен

Квадратный трёхчлен — это многочлен вида ax 2 + bx + c .

В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:

Левая часть этого уравнения является квадратным трёхчленом.

Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.

Полученные корни x₁ и x₂ следует подстáвить в следующее выражение, которое и станет разложением:

Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:

Где левая часть — исходный квадратный трёхчлен.

Пример 1. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:

В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:

Итак, x₁ = 6 , x₂ = 2 . Теперь воспользуемся формулой ax 2 + bx + c = a(x − x₁)(x − x₂). В левой части вместо выражения ax 2 + bx + c напишем свой квадратный трёхчлен x 2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x₁ = 6, x₂ = 2

Если a равно единице (как в данном примере), то решение можно записать покороче:

Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.

Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2) . Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x 2 − 8x + 12

Пример 2. Разложить на множители следующий квадратный трёхчлен:

Приравняем данный квадратный трёхчлен к нулю и решим уравнение:

Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:

Итак, x₁ = 4 , x₂ = 3 . Приравняем квадратный трехчлен 2x 2 − 14x + 24 к выражению a(x − x₁)(x − x₂) , где вместо переменных a , x₁ и x₂ подстáвим соответствующие значения. В данном случае a = 2

Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24

Видео:Разложение на множители. 7 класс. Вебинар | МатематикаСкачать

Как это работает

Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.

Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:

Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:

Тогда приведённый квадратный трехчлен x 2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x₁ + x₂ = −b . Для этого можно умножить обе его части на −1

Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:

Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c

Раскроем скобки там где это можно:

В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:

Из первых скобок вынесем общий множитель x , из вторых скобок — общий множитель −x₂

Далее замечаем, что выражение ( x − x₁ ) является общим множителем. Вынесем его за скобки:

Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.

Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a

Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax 2 + bx + c = 0 , то теорема Виета принимает следующий вид:

Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a

Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства 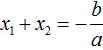и

Для начала выразим b и c . В первом равенстве умножим обе части на a . Затем обе части получившегося равенства умножим на −1

Теперь из второго равенства выразим c . Для этого умножим обе его части на a

Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax 2 + bx + c . Для наглядности каждое преобразование будем выполнять на новой строчке:

Здесь вместо переменных b и c были подставлены выражения −ax₁ − ax₂ и ax₁x₂ , которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:

В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:

Теперь из первых скобок вынесем общий множитель ax , а из вторых — общий множитель −ax₂

Далее замечаем, что выражение x − x₁ тоже является общим множителем. Вынесем его за скобки:

Вторые скобки содержат общий множитель a . Вынесем его за скобки. Его можно расположить в самом начале выражения:

Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x₁)(x − x₂) вместо переменных x₁ и x₂ .

Если квадратный трёхчлен имеет только один корень, то этот корень одновременно подставляется в x₁ и x₂ . Например, квадратный трёхчлен x 2 + 4x + 4 имеет только один корень −2

Тогда значение −2 в процессе разложения на множители будет подставлено вместо x₁ и x₂ . А значение a в данном случае равно единице. Её можно не записывать, поскольку это ничего не даст:

Скобки внутри скобок можно раскрыть. Тогда получим следующее:

При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Примеры разложений

Пример 1. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x 2 − 2x − 1 , а в правой части — его разложение в виде a(x − x₁)(x − x₂) , где вместо a , x₁ и x₂ подстáвим соответствующие значения:

Во вторых скобках можно заменить вычитание сложением:

Пример 2. Разложить на множители следующий квадратный трёхчлен:

Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3

Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:

Пример 3. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Пример 4. Найдите значение k , при котором разложение на множители трёхчлена 3x 2 − 8x + k содержит множитель (x − 2)

Если разложение содержит множитель (x − 2) , то один из корней квадратного трёхчлена равен 2 . Пусть корень 2 это значение переменной x₁

Чтобы найти значение k , нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета.

В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби , а произведение корней — дроби

Выразим из первого равенства переменную x₂ и сразу подстáвим найденное значение во второе равенство вместо x₂

Теперь из второго равенства выразим k . Так мы найдём его значение.

Пример 5. Разложить на множители следующий квадратный трёхчлен:

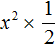
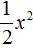
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим . Если поменять местами сомножители, то получится . То есть коэффициент a станет равным

Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Видео:Теорема Безу и разложение многочлена на множителиСкачать

Задания для самостоятельного решения

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

📽️ Видео

ОГЭ. Задание 21. Уравнение третей степени. Разложение на множители.Скачать

Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать

Применение различных способов для разложения на множители. Алгебра, 7 классСкачать

Математика| Разложение квадратного трехчлена на множители.Скачать

Разложение на множители. ПримерыСкачать

Решение уравнений в 7 классе с помощью разложения многочленов на множители. Алгебра 7-11 класс.Скачать

Решение уравнений с помощью разложения на множители.Скачать

7 класс, 30 урок, Разложение многочленов на множители с помощью формул сокращённого умноженияСкачать

Решение логарифмических уравнений ПРИМЕР #10 Метод разложения на множителиСкачать

Схема Горнера. 10 класс.Скачать

Разложение квадратного трехчлена на множители. 8 класс.Скачать