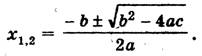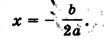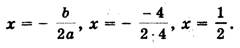Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать
1. СПОСОБ: Разложение левой части уравнения на множители.
1. СПОСОБ : Разложение левой части уравнения на множители.
Решим уравнение х 2 + 10х — 24 = 0. Разложим левую часть на множители:
х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х 2 + 10х — 24 = 0.
Видео:Разложение кубических выражений на множителиСкачать
СПОСОБ: Разложение левой части уравнения на множители
1. СПОСОБ: Разложение левой части уравнения на множители.
х 2 + 10х — 24 = 0.
Разложим левую часть на множители:
х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х 2 + 10х — 24 = 0.
2. СПОСОБ: Метод выделения полного квадрата.
Решим уравнение х 2 + 6х — 7 = 0.
Выделим в левой части полный квадрат.
Для этого запишем выражение х 2 + 6х в следующем виде:
х 2 + 6х = х 2 + 2• х • 3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 3 2 , так как
х 2 + 2• х • 3 + 3 2 = (х + 3) 2 .
Преобразуем теперь левую часть уравнения
прибавляя к ней и вычитая 3 2 . Имеем:
х 2 + 6х — 7 = х 2 + 2• х • 3 + 3 2 — 3 2 — 7 = (х + 3) 2 — 9 — 7 = (х + 3) 2 — 16.
Таким образом, данное уравнение можно записать так:
(х + 3) 2 — 16 =0, (х + 3) 2 = 16.
Следовательно, х + 3 — 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
3. СПОСОБ: Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах 2 + bх + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а 2 х 2 + 4аbх + 4ас = 0,
((2ах) 2 + 2ах • b + b 2 ) — b 2 + 4ac = 0,
(2ax + b) 2 = b 2 — 4ac,
2ax + b = ± √ b 2 — 4ac,
2ax = — b ± √ b 2 — 4ac,
а) Решим уравнение: 4х 2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b 2 — 4ac = 7 2 — 4 • 4 • 3 = 49 — 48 = 1,
D > 0, два разных корня;
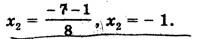
Таким образом, в случае положительного дискриминанта, т.е. при
b 2 — 4ac >0 , уравнение ах 2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х 2 — 4х + 1 = 0,
а = 4, b = — 4, с = 1, D = b 2 — 4ac = (-4) 2 — 4 • 4 • 1= 16 — 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b 2 — 4ac = 0, то уравнение
ах 2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х 2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b 2 — 4ac = 3 2 — 4 • 2 • 4 = 9 — 32 = — 13 , D 2 — 4ac 2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах 2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х 2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
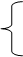
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р 2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 > 0 и p = — 3 2 + 8x + 7 = 0; x1 = — 7 и x2 = — 1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q 0 .
x 2 + 4x – 5 = 0; x1 = — 5 и x2 = 1, так как q= — 5 0;
Видео:Алгебра 10 класс (Урок№12 - Решение алгебраических уравнений разложением на множители.)Скачать
«Решение уравнений высших степеней». 9-й класс
Разделы: Математика
Класс: 9
Учебная:
Развивающая:
- Развитие внимания учащихся.
- Развитие умения добиваться результатов труда.
- Развитие интереса к изучению алгебры и навыков самостоятельной работы.
Воспитывающая:
Оборудование: компьютер, проектор.
1 этап работы. Организационный момент.
2 этап работы. Мотивация и выход на постановку проблемы
Уравнение 
одно из важнейших понятий математики. Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры.
В школьном курсе изучения математики очень много внимания уделяется решению различного вида уравнений. До девятого класса мы умели решать только линейные и квадратные уравнения. Уравнения третьей, четвёртой и т.д. степеней называются уравнениями высших степеней. В девятом классе мы познакомились с двумя основными приёмами решения некоторых уравнений третьей и четвёртой степеней: разложение многочлена на множители и использование замены переменной.
А можно ли решить уравнения более высоких степеней? На этот вопрос мы постараемся сегодня найти ответ.
3 этап работы. Повторить ранее изученный материал. Ввести понятие уравнения высших степеней.
1) Решение линейного уравнения.
Линейным называется уравнение вида 
, где 
по определению. Такое уравнение имеет единственный корень 
.
2) Решение квадратного уравнения.
Квадратным называется уравнение вида 
, где 
. Количество корней и сами корни определяются дискриминантом уравнения 
. Для 
уравнение корней не имеет, для 
имеет один корень (два одинаковых корня)
, для 
имеет два различных корня 
.
Из рассмотренных линейных и квадратных уравнений видим, что количество корней уравнения не более его степени. В курсе высшей алгебры доказывается, что уравнение 
-й степени 
имеет не более n корней. Что касается самих корней, то тут ситуация намного сложнее. Для уравнений третьей и четвёртой степеней известны формулы для нахождения корней. Однако эти формулы очень сложны и громоздки и практического применения не имеют. Для уравнений пятой и более высоких степеней общих формул не существует и существовать не может (как было доказано в XIX в. Н. Абелем и Э. Галуа).
Будем называть уравнения третьей, четвёртой и т.д. степеней уравнениями высших степеней. Некоторые уравнения высоких степеней удаётся решить с помощью двух основных приёмов: разложением многочлена 
на множители или с использованием замены переменной.
3) Решение кубического уравнения.
Решим кубическое уравнение 
Сгруппируем члены многочлена, стоящего в левой части уравнения, и разложим на множители. Получим:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три линейных уравнения:
Итак, данное кубическое уравнение имеет три корня: 
; 
;
.
4) Решение биквадратного уравнения.
Очень распространены биквадратные уравнения, которые имеют вид 
(т.е. уравнения, квадратные относительно 
). Для их решения вводят новую переменную 
.
Решим биквадратное уравнение 
.
Введём новую переменную и получим квадратное уравнение 
, корнями которого являются числа 
и 4.
Вернёмся к старой переменной 
и получим два простейших квадратных уравнения:
(корни и 
)
(корни 
и 
)
Итак, данное биквадратное уравнение имеет четыре корня:
; ;
.
Попробуем решить уравнение 
используя выше изложенные приёмы.
4 этап работы. Привести некоторые утверждения о корнях многочлена вида 
, где 
многочлен n-й степени
Приведём некоторые утверждения о корнях многочлена вида :
1) Многочлен -й степени имеет не более корней (с учётом их кратностей). Например, многочлен третьей степени не может иметь четыре корня.
2) Многочлен нечётной степени имеет хотя бы один корень. Например, многочлены первой, третьей, пятой и т.д. степени имеют хотя бы один корень. Многочлены чётной степени корней могут и не иметь.
3) Если на концах отрезка 
значения многочлена имеют разные знаки (т.е. ,
), то на интервале 
находится хотя бы один корень. Это утверждение широко используется для приближенного вычисления корней многочлена.
4) Если число 
является корнем многочлена вида , то этот многочлен можно представить в виде произведения 
, где 
многочлен (
-й степени. Другими словами, многочлена вида можно разделить без остатка на двучлен 
. Это позволяет уравнение -й степени сводить к уравнению (-й степени (понижать степень уравнения).
5) Если уравнение 
со всеми целыми коэффициентами (причём свободный член 
) имеет целый корень , то этот корень является делителем свободного члена 
. Такое утверждение позволяет подобрать целый корень многочлена (если он есть).
5 этап работы. Показать как применяется теория делимости для решения уравнений высших степеней. Рассмотреть примеры решения уравнений высших степеней , в которых для разложения левой части на множители используется способ деления многочлена на многочлен “уголком”.
Пример 1. Решим уравнение 
.
Если это уравнение имеет целый корень, то он является делителем свободного члена (-1), т.е. равняется одному из чисел: 
. Проверка показывает, что корнем уравнения является число -1. Значит, многочлен 
можно представить в виде произведения 
, т.е. многочлен 
можно без остатка разделить на двучлен 
. Выполним такое деление “уголком”:
Таким образом, мы фактически разложили левую часть уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем два уравнения:
Итак, данное уравнение имеет три корня:
Пример 2. Решим уравнение 
.
Если это уравнение имеет целый корень, то он является делителем свободного члена (9),т.е. равняется одному из чисел: ;
. Проверим:
Значит, многочлен 
можно представить в виде произведения 
, т.е. многочлен 
можно без остатка разделить на двучлен . Выполним такое деление “уголком”:
Таким образом, мы разложили левую часть уравнения на множители:
Аналогичным образом поступим и с многочленом 
.
Если это уравнение 
имеет целый корень, то он является делителем свободного члена (9), т.е. равняется одному из чисел: ;. Проверим:
Значит, многочлен можно представить в виде
произведения 
, т.е. многочлен можно без остатка разделить на двучлен 
. Выполним такое деление “уголком”:
Таким образом, мы разложили левую часть исходного уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три уравнения:
Итак, данное уравнение имеет четыре корня:
6 этап работы. Закрепление изученного материала.
Решите уравнения высших степеней, используя способ деления многочлена на многочлен “уголком”.
7 этап работы. Вывод урока.
Решить уравнения высших степеней можно следующим образом:
- используя формулы для нахождения корней (если они известны);
- используя замену переменной;
- раскладывая многочлен в левой части уравнения на множители, используя способ деления многочлена на многочлен “уголком”.
8 этап работы. Домашнее задание.
Дома решить уравнения высших степеней, используя способ деления многочлена на многочлен “уголком” (раздать листы с заданиями).
📹 Видео
Решение уравнений с помощью разложения на множители | Алгебра 7 класс #23 | ИнфоурокСкачать
Задание 21 Разложение левой части уравнения на множителиСкачать
Решаем тригонометрические уравнения через разложение на множители или деление на косинус вСкачать
Математика| Разложение квадратного трехчлена на множители.Скачать
Тригонометрические уравнения. Метод разложения на множители.Скачать
Разложение на множители. 7 класс. Вебинар | МатематикаСкачать
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
Решение тригонометрических уравнений и их систем. 10 класс.Скачать
10 класс. Алгебра. Тригонометрические уравнения, решаемые разложением левой части на множителиСкачать
Решение тригонометрических уравнений. 10 класс.Скачать
Решение логарифмических уравнений ПРИМЕР #10 Метод разложения на множителиСкачать
Решение уравнений с помощью разложения на множители.Скачать
Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать
Методы решения тригонометрических уравнений Разложение на множителиСкачать
Решение уравнений в 7 классе с помощью разложения многочленов на множители. Алгебра 7-11 класс.Скачать
РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ / Алгебра 7 классСкачать
Решение алгебраических уравнений разложением на множителиСкачать
