- Формулами сокращенного умножения (ФСУ) называют несколько наиболее часто встречающихся в практике случаев умножения многочленов.
- Квадрат суммы
- Квадрат суммы: ((a+b)^2=a^2+2ab+b^2)
- Квадрат разности
- Квадрат разности: ((a-b)^2=a^2-2ab+b^2)
- Разность квадратов
- Разность квадратов (a^2-b^2=(a+b)(a-b))
- Тема урока: «Решение линейных уравнений, содержащих формулы сокращенного умножения»
- решение уравнений на формулы сокращённого умножения
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 🔥 Видео
Формулами сокращенного умножения (ФСУ) называют несколько наиболее часто встречающихся в практике случаев умножения многочленов.
ФСУ используются при упрощении алгебраических выражений (в том числе в работе с алгебраическими дробями ), решении уравнений и неравенств , при разложении на множители и т.д. Ниже мы рассмотрим наиболее популярные формулы и разберем как они получаются.
Видео:Формулы сокращенного умножения | Математика | TutorOnlineСкачать

Квадрат суммы
Пусть у нас возводиться в квадрат сумма двух одночленов, вот так: ((a+b)^2). Возведение в квадрат – это умножение числа или выражения само на себя, то есть, ((a+b)^2=(a+b)(a+b)). Теперь мы можем просто раскрыть скобки, перемножив их как делали это здесь , и привести подобные слагаемые. Получаем:
А если мы опустим промежуточные вычисления и запишем только начальное и конечное выражения, получим окончательную формулу:
Квадрат суммы: ((a+b)^2=a^2+2ab+b^2)
Большинство учеников учат ее наизусть. А вы теперь знаете, как эту формулу вывести, и если вдруг забудете – всегда можете это сделать.
Хорошо, но как ей пользоваться и зачем эта формула нужна? Квадрат суммы позволяет быстро писать результат возведения суммы двух слагаемых в квадрат. Давайте посмотрим на примере.
Обратите внимание, насколько быстрее и меньшими усилиями получен результат во втором случае. А когда вы эту и другие формулы освоите до автоматизма – будет еще быстрее: вы сможете просто сразу же писать ответ. Поэтому они и называются формулы СОКРАЩЕННОГО умножения. Так что, знать их и научиться применять – точно стоит.
На всякий случай отметим, что в качестве (a) и (b) могут быть любые выражения – принцип остается тем же. Например:
Если вы вдруг не поняли какие-то преобразования в двух последних примерах – повторите свойства степеней и тему приведения одночлена к стандартному виду .
Пример. Преобразуйте выражение ((1+5x)^2-12x-1 ) в многочлен стандартного вида.
Раскроем скобки, воспользовавшись формулой квадрата суммы.
…и приведем подобные слагаемые.
Важно! Необходимо научиться пользоваться формулами не только в «прямом», но и в «обратном» направлении.
Пример. Вычислите значение выражения ((368)^2+2·368·132+(132)^2) без калькулятора.
Мда… возводить в квадрат трехзначные числа, перемножить их же, а потом все это складывать – удовольствие ниже среднего. Давайте искать другой путь: обратите внимание, что данное нам числовое выражение очень похоже на правую часть формулы. Применим ее в обратную сторону: (a^2+2ab+b^2=(a+b)^2)
Вот теперь вычислять гораздо приятнее!
Видео:Решить уравнения, используя формулы сокращенного умножения.Сумма и квадрат разности. Алгебра 7 классСкачать

Квадрат разности
Выше мы нашли формулу для суммы одночленов. Давайте теперь найдем формулу для разности, то есть, для ((a-b)^2):
В более краткой записи имеем:
Квадрат разности: ((a-b)^2=a^2-2ab+b^2)
Применяется она также, как и предыдущая.
Пример. Упростите выражение ((2a-3)^2-4(a^2-a)) и найдите его значение при (a=frac).
Если сразу подставить дробь в выражение – придется возводить ее в квадрат и вообще делать объемные вычисления. Попробуем сначала упростить выражение, воспользовавшись формулой выше и раскрыв скобки .
Теперь приведем подобные слагаемые.
Вот теперь подставляем и наслаждаемся простотой вычислений.
Видео:7 класс, 24 урок, Формулы сокращённого умноженияСкачать

Разность квадратов
Итак, мы разобрались с ситуациями произведения двух скобок с плюсом в них и двух скобок с минусом. Остался случай произведения одинаковых скобок с разными знаками. Смотрим, что получится:
Разность квадратов (a^2-b^2=(a+b)(a-b))
Эта формула одна из наиболее часто применяемых при разложении на множители и работе с алгебраическими дробями .
Да, я знаю, что рука так и тянется сократить иксы и девятку с тройкой – однако так делать ни в коем случае нельзя, ведь и в числителе, и в знаменателе стоит минус!
Попробуем воспользоваться формулой.
Вот теперь все плюсы и минусы попрятались в скобки, и значит без проблем можем сокращать одинаковые скобки.
Воспользуемся формулами степеней: ((a^n )^m=a^) и (a^n b^n=(ab)^n).
Ну, а теперь пользуемся формулой (a^2-b^2=(a+b)(a-b)), где (a=5x^2) и (b=m^5 t^3).
Это три основные формулы, знать которые нужно обязательно! Есть еще формулы с кубами (см. выше), их тоже желательно помнить либо уметь быстро вывести. Отметим также, что в практике часто встречаются сразу несколько таких формул в одной задаче – это нормально. Просто приучайтесь замечать формулы и аккуратно применяйте их, и все будет хорошо.
На первый взгляд тут тихий ужас и сделать с ним ничего нельзя (вариант «лечь и помереть» всерьез не рассматриваем).
Однако давайте попробуем поменять два последних слагаемых числителя местами и добавим скобки (просто для наглядности).
Теперь немного преобразуем слагаемые в скобке:
(4xy) запишем как (2·x·2y),
а (4y^2) как ((2y)^2).
Теперь приглядимся – и заметим, что в скобке у нас получилась формула квадрата разности, у которой (a=x), (b=2y). Сворачиваем по ней к виду скобки в квадрате. И одновременно представляем девятку как (3) в квадрате.
Еще раз внимательно смотрим на числитель… думаем… думаем… и замечаем формулу разности квадратов, у которой (a=(x-2y)), (b=3). Раскладываем по ней к произведению двух скобок.
И вот теперь сокращаем вторую скобку числителя и весь знаменатель.
Видео:РЕШЕНИЕ УРАВНЕНИЙ С ПРИМЕНЕНИЕМ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ. 7 КЛСкачать

Тема урока: «Решение линейных уравнений, содержащих формулы сокращенного умножения»
Разделы: Математика
Цели урока:
- Обработка рациональных приёмов решения уравнений.
- Выработка умения решения задач.
- Развитие элементов творческой деятельности учащихся и умения контролировать свои действия.
- Повторение решения уравнений.
Оборудование: печатные бланки, таблица.
Тип урока: урок- семинар комплексного применения знаний, умений и навыков.
1.Организационный момент. Сообщается план семинара.
2.Сообщение по теме « Уравнение»
3. Решение линейных уравнений.
4.Сообщение о формулах сокращённого умножения.
(Работа у доски и по карточкам.)
а) Решение уравнений, содержащих квадрат суммы.
б) Решение уравнений, содержащих квадрат разности.
в) Решение квадратных уравнений, содержащих разность квадрата.
г) Решение уравнений, содержащих несколько формул.
5. Решение задачи.
6. Творческая работа учащихся.
7. Подведение итогов урока.
Ход урока.
1.Вступительное слово учителя.
Один начинающий волшебник, герой шуточной песенки, неумело обращался с заклинаниями, в результате вместо грозы у него получилась коза, а вместо утюга слон. Чтобы решить уравнение, тоже нужно совершить ряд превращений (алгебраических преобразований) и делать их нужно очень осмотрительно. Сегодня мы ещё раз увидим, какая удивительная сила заключена в формулах сокращённого умножения и как ловко они работают при решении уравнений.
Прежде всего, нужно чётко понимать, чем вы занимаетесь, когда решаете уравнение. Что, значит, решить уравнение и нужно знать, что главная задача при решении любого уравнения — свести его к простейшему.
И сегодня нам будут помогать формулы Сокращённого умножения.
2. Сообщение по теме «Уравнение»
3. Решение линейных уравнений у доски (учащиеся класса записывают решения в тетрадях)
| а) 2-3(x+2)=5-2x; 2-3x-6=5-2x, -3x+2x=5-2+6 -x =9 x=-9 Ответ:-9. | б) 20+4(2x-5)=14x+12 20+8x-20=14x+12, 8x-14x=12, -6x=12, x=-2, Ответ: -2. |
Решение уравнений по карточкам.
в) 4(2-3x)+7(6x+1)-9(9x+4)=30
г) 3-5(x+1)=6-4x.
Сообщение №2.
Слово о формулах.
4. Решение уравнений, содержащих квадрат суммы и квадрат разности.
а) x+(5x+2)2 =25(1+x2).
б) (x-6)2-x(x+8)=2.
Решение уравнений по карточкам.
в) (2-x)2-x(x+1,5)=4
г) x(x-1)-(x-5)2=2.
5. Решение уравнений, в которых содержится формула разности квадратов.
Работа у доски.
8x(1+2x)-(4x+3)(4x-3)=2x.
8x+16×2-(16×2-9)=2x,
8x+16×2-(16×2-9)=2x,
8x+16×2-16×2+9=2x,
8x-2x=-9,
6x=-9,
x=-1,5
Ответ: -1,5
Решение задачи.
Сторона первого квадрата на 2см. больше стороны второго, а площадь первого на 12 см больше площади второго. Найдите периметры этих квадратов.
Пусть x см сторона второго квадрата. Тогда(x+2) см сторона первого квадрата. Площадь первого (x+2) 2 см 2 ,а площадь второго x 2 .
Составляем уравнение:
(x+2) 2 -x 2 =12
x 2 +4x+4-x 2 =12,
4x=12-8,
4x=8,
x=2.
Если x=2,то 4x=4*2=8
Если x=2, то 4(x+2)=4(2+2)=16.
Ответ:16см,8см.
6. Решение разных уравнений, содержащих формулы сокращённого умножения.
7.Творческая работа учащихся. Заполнение таблицы.
Узнайте фамилию величайшего математика XVII века. Для этого зачеркните
буквы, не связанные с найденными ответами.
(Декарт)
| -9 | 8,2 | -2 | 3,4 | 1 | 3,1 | 1,7 | 15 | -1,5 | 17 | 11 | 3 |
| Д | П | Е | Ф | К | С | А | И | Р | Г | Ш | Т |
Приложение к уроку.
Решение линейных уравнений.
| 4(2-3x)+7(6x+1)-9(9x+4)=30 8-12x+42x+7-81-36=30, 51x-21=30, 51x=51 x=1 Ответ: 1. | 3-5(x+1)=6-4x, 3-5x-5=6-4x, -5x+4x=6-3+5, -x=8x= -8. Ответ:-8. |
Решение уравнений, содержащих квадрат суммы и квадрат разности.
| x+(5x+2) 2 =25(1+x 2 ) x+(25x 2 +20+4)=25(1+x 2 ) x+25x 2 +20x+4=25+25x 2 , 21x+25x 2 -25x 2 =25-4, 21x=21 x=1 Ответ:1. | (x -6) 2 -x(x+8)=2 x 2 -12x+36-x 2 -8x=2 -20x=2-36, -20x=-34, x=1,7 Ответ: 1,7. |
Работа по карточкам.
| (2-x)2-x(x+1,5)=4, 4-4x+x 2 -x 2 -1,5x=4, -4x-1,5x=4-4, -5,5 x=0 Ответ:0. | x(x-1)-(x-5) 2 =2 x 2 -x-(x 2 -10x+25)=2, x 2 -x-x 2 +10x-25=2 9x=27 x=3 Ответ: 3. |
Решение разных уравнений содержащих несколько формул сокращённого умножения.
| (x-4x)+(x+4)+(3x-4)(x+2)=(2x+3) 2 x 2 -16+3x 2 +6x-4x-8=4x 2 +12x+9 -10x=33 x=-3,3 Ответ:3,3. | ( 2x+3)2-4(x-1)(x+1)=49 4x 2 +12x+9-4(x 2 -1)=49 4x 2 +12x+9-4x 2 +4=49 12x+13=49 12x=36 X=3 Ответ: 3. |
8. Подведение итогов урока.
Видео:Как раз и навсегда выучить формулы сокращенного умноженияСкачать
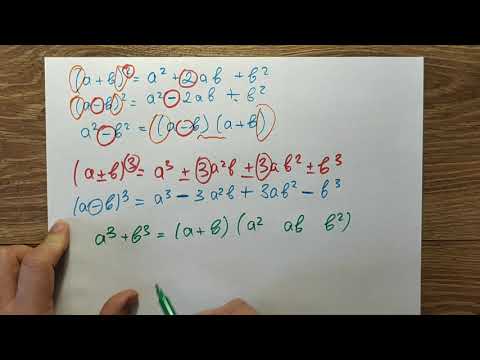
решение уравнений на формулы сокращённого умножения
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Решение уравнений на формулы сокращённого умножения с построением на плоскости. 7 класс.
1. (х – 7) 2 + 3 = (х — 2) ∙ (х +2)
8. ( 4х – 3)∙(3+4х) – 2х∙(8х – 1) = 0
2. (х +1) ∙ (х +2) – (х — 3) ∙ (х + 4) = 6
9. (3х -1)∙( 2х +7) – ( х+1)∙( 6х – 5) = 7
3. 8 m ∙(1+ 2 m ) – (4 m + 3)∙(4 m – 3) = 2 m
10. х — 3х∙(1 – 12х) = 11 – (5 – 6х)∙(6х + 5)
4. (2х – 3) 2 – 2х∙ (4 + 2х) = 11
11. (2х – 3) 2 – (7 – 2х) 2 = 2
5. (8 – 9а)∙а = — 40 + (6 – 3а)∙(6 + 3а)
12. 24 –( 3у + 1)∙( 4у – 5) = (11 – 6у)∙(2у – 7)
6. ( х + 6) 2 – (х -5)∙(х + 5) = 79
13. ( 6х – 1)∙(6х + 1) – 4х∙(9х + 2) = -1
7. (6у +2)∙(5 –у) = 47–(2у -3)∙(3у – 1)
14. ( 5х – 1) 2 – ( 1 – 3х) 2 = 16х∙(х – 3)
Краткое описание документа:
После того, как изучили формулы сокращённого умножения,решила немного разнообразить работу на уроке и тем самымрешить несколько проблем сразу: повторить решение уравнений, закрепить умение пользоваться формулами на практике, повторение построений на координатной плоскости. Работа заключается в следующем: дети решают уравнения, находят в во втором столбике таблицы ответ и соответствующую ему координату. Затем, по этим координатам они строят фигуру. Учащимся такая работа очень нравится.Они с удовольствием решают уравнения, стараясь быстрее узнать, что за рисунок спрятан. Желаю успеха всем ученикам. которые будут решать эти уравнения.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 939 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 686 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 313 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Алгебра 7. Урок 5 - Формулы сокращенного умножения - применение.Скачать

Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 589 972 материала в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 19.02.2015
- 789
- 1
- 19.02.2015
- 498
- 1
- 19.02.2015
- 1540
- 0
- 19.02.2015
- 4041
- 4
- 19.02.2015
- 1928
- 0
- 19.02.2015
- 681
- 0
- 19.02.2015
- 29911
- 297
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 19.02.2015 8382
- DOCX 59.5 кбайт
- 129 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Широкая Ольга Валерьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет и 1 месяц
- Подписчики: 0
- Всего просмотров: 104534
- Всего материалов: 12
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Решение уравнений с формулами сокращенного умножения, 7 классСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
Университет им. Герцена и РАО создадут портрет современного школьника
Время чтения: 2 минуты
В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Время чтения: 1 минута
В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Каждый второй ребенок в школе подвергался психической агрессии
Время чтения: 3 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Только 23 февраля!
Получите новую
специальность
по низкой цене
Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки
🔥 Видео
Алгебра 7. Урок 4 - Формулы сокращенного умножения и как их запомнить.Скачать

Алгебра 7 класс. Решение уравнений с использованием формул сокращенного умножения.Скачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Квадрат суммы и квадрат разности двух выражений. 7 класс.Скачать

Алгебра 7 класс (Урок№32 - Применение формул сокращённого умножения. Разложение многочленов.)Скачать

7 класс, 30 урок, Разложение многочленов на множители с помощью формул сокращённого умноженияСкачать

#110 Урок 35. Вычисление значений корня при помощи формул сокращенного умножения. Алгебра 8 класс.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Алгебра 8 класс. Сокращение дробей с формулами сокращенного умноженияСкачать

Формлы сокращенного умножения. Алгебра 7 класс. Решите уравнение.Скачать

Многочлены. Формулы сокращенного умножения. Примеры ( Алгебра 7 класс )Скачать

Разложение многочленов на множители.Метод #2, использование ФСУ(формул сокращенного умножения).Скачать

18. Геометрическая задача на параллелепипед с применением формулы сокращённого умноженияСкачать









