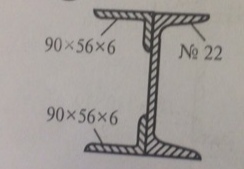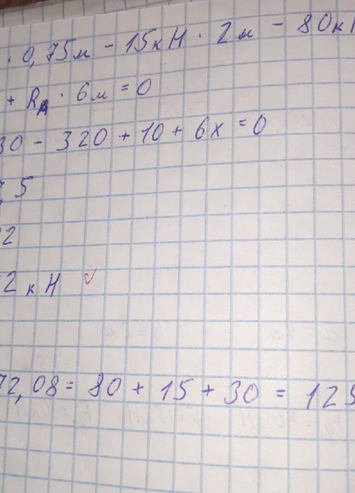- Решение задач по технической механике
- Примеры решения задач по теоретической механике
- Материалы для скачивания
- Ответы на задачи по технической механике
- Полезные материалы
- Оконный кондиционер
- Mitsubishi MS-GF25/MU-GF25VA — 54700 руб.
- Ремонт системы чиллер-фанкойл
- Руководства
- DAIKIN Ururu Sarara FTXR28E/RXR25E — 71550р.
- О Компании
- Меню опросов
- Контакты
- Задачи по теоретической механике с подробными решениями
- Подробные решения задач по теоретической механике
- Статика
- Кинематика
- Кинематика материальной точки
- Поступательное и вращательное движение твердого тела
- Кинематический анализ плоского механизма
- Определение абсолютной скорости и абсолютного ускорения точки
- Динамика
- Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
- Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
- Теорема об изменении кинетической энергии механической системы
- Применение общего уравнения динамики к исследованию движения механической системы
- Применение принципа Даламбера к определению реакций опор вращающегося тела
- 🌟 Видео
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Решение задач по технической механике
Примеры решения задач по теоретической механике
Принципы и способы решения задач теоретической механики рассмотрены на простейших примерах, где необходимо определить какие-либо силовые факторы, действующие на тело, скорость, ускорение, работу, мощность и другие физические величины. На основе результатов расчетов с использованием приемов теоретической механики приступают к решению задач методами сопротивления материалов, а затем переходят к расширенным практическим вопросам, которые ставит раздел «Детали машин».
Решение задачи с использованием метода кинетостатики
Определить силу натяжения в канате крановой установки, поднимающей груз G с ускорением а .
Масса груза m = 5 тонн;
Ускорение груза а = 2 м/сек 2 ;
Ускорение свободного падения принять равным g = 10 м/сек 2 ;
Силой сопротивления воздуха пренебречь.
Для решения задачи используем метод кинетостатики (принцип Д’Аламбера), который основывается на введении понятия силы инерции и приведении подвижной системы к состоянию условного равновесия. Это позволяет использовать для решения задач Кинематики способы и методы Статики.
Чтобы понять сущность этого принципа, представьте себе просмотр киносюжета, кадры которого сняты при малой скоростью съемки, и движение тел на экране словно состоит из отдельных прерывистых фрагментов (или — как передвигается робот — урывками). Т. е. движение тела рассматривается состоящим из отдельных крохотных моментов, и в каждый такой микромомент тело находится в состоянии равновесия под действием движущей силы и силы инерции, сопротивляющейся движению.
Следует отметить, что сила инерции – понятие условное. Тем не менее, инертность тел – явление известное всем, поскольку, например, тяжелый шар трудно сдвинуть с места, а когда он, все-таки, покатится, его трудно остановить.
Итак, для решения этой задачи следует рассмотреть условие равновесия груза, который поднимается с ускорением а под действием некоторой системы сил. Реально к грузу приложены две силы – сила натяжения каната, и сила тяжести груза. Очевидно, что эти силы не равны по величине, поскольку груз поднимается с ускорением, значит, сила натяжения в канате больше силы тяжести.
Введем в систему упомянутую выше силу инерции, которая условно уравнивает разницу между силой натяжения в канате и силой тяжести, тогда груз будет находиться в условном равновесии.
Составим уравнение этого равновесия: Fк – G – F ин = 0 ,
где: Fк – сила натяжения каната (тяга крановой установки), G – вес груза, F ин – сила инерции.
Очевидно, что условие равновесия будет соблюдаться, если искомая сила Fк будет равна сумме сил тяжести и инерции.
Силу тяжести G и силу инерции F ин можно вычислить, используя второй закон Ньютона, как произведение массы тела на ускорение, вызываемое этими силами:
G = mg, где m – масса тела в кг, g – ускорение свободного падения;
Fин = ma, тогда:
Fк = G + F ин = mg + ma = m(g + a) = 5000 × (10 + 2) = 60 000 Н = 60 кН .
Решение задачи на на трение
Определить силу F , необходимую для равномерного перемещения бруса по горизонтальной шероховатой поверхности.
Коэффициент трения между брусом и поверхностью f = 0,6;
Масса бруса m = 12 кг;
Ускорение свободного падения g принять равным 10 м/сек 2 .
Эта задача решается с использованием законов движения тел под действием сил трения скольжения.
Для того, чтобы тело равномерно перемещалось по поверхности без ускорения, сила трения должна быть равна силе тяги (т. е. искомой силе F): F = Fтр.
Поскольку поверхность горизонтальная, сила трения равна весу тела, умноженному на коэффициент трения:
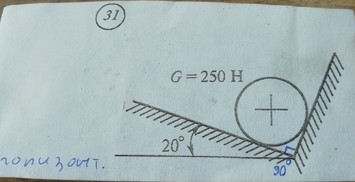
Решение задачи из раздела Статика

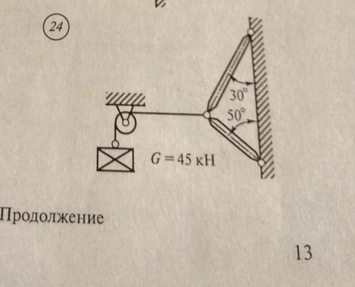
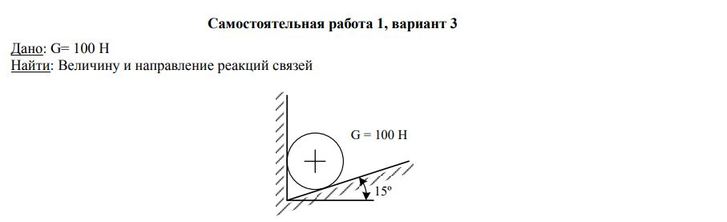
Вес груза G = 100 Н,
угол наклона поверхности указан на рисунке.
Поскольку груз находится в равновесии, решение задачи возможно с применением методов Статики, т. е. с на основе анализа причин, по которым тело находится в неподвижном состоянии (в равновесии) .
Итак, сначала необходимо определить – под влиянием каких сил груз находится в состоянии равновесия.
Кроме силы тяжести G , на груз наложены две связи, ограничивающие его перемещение: гибкая связь (упругая нить) и наклонная плоскость. Реакция гибкой связи Rн направлена вдоль линии этой связи (вдоль нити), а реакция плоскости Rп всегда перпендикулярна этой плоскости и приложена в точке касания телом плоскости (см. схему).
Задача может быть решена двумя методами.
Определив направление реакций, можно решить эту задачу графическим методом, построив силовой треугольник, который будет замкнутым, поскольку векторная сумма сил равна нулю (равновесие груза).
Для построения векторной цепочки (в нашем случае – треугольник) откладываем силу тяжести груза G в определенном масштабе (поскольку нам известны и направление, и величина этой силы).

Аналитическим методом эта задача решается с помощью уравнений равновесия, исходя из условия, что сумма проекций всех сил на любую координатную ось равна нулю. Разумеется, необходимо выбрать удобную систему координат, тогда для решения задачи потребуется минимальное количество уравнений.
В нашем случае можно любую из координат расположить так, чтобы одна из неизвестных реакций была ей перпендикулярна, тогда проекция этой силы на данную координатную ось будет равна нулю.
Поскольку нам необходимо найти силу натяжения нити (реакция Rн ), то расположим координатную ось y так, чтобы реакция плоскости ( Rп ) была ей перпендикулярна (рис. в). Тогда реактивная сила Rп проецируется в точку, т. е. в ноль, и для решения задачи потребуется лишь сумма проекций сил G и Rн на ось y :
ΣFy = 0 => Rн – G cos60˚ = 0, откуда найдем искомую реакцию Rн :
Rн = G cos60˚ = 100×0,5 = 50 Н .
Задача решена двумя методами.
Пример решения задачи из раздела Динамика
Какую работу W необходимо совершить, чтобы повалить кубический предмет на боковую грань?
Длина грани кубического предмета (ящика) a = 1 м;
Масса кубического предмета m = 100 кг;
Центр тяжести кубического предмета расположен в точке пересечения диагоналей;
Ускорение свободного падения принять равным g = 10 м/сек 2
Как известно, работа любой силы равна произведению модуля этой силы на величину перемещения тела, вызванного действием этой силы.
Искомая работа W равна работе по преодолению силы тяжести при подъеме центра масс ящика на высоту Δh , равную разности между половиной диагонали боковой грани ящика и половиной длины его стороны, т.е. – вся работа заключается в постановке ящика на ребро А .
Длину диагонали грани можно найти по теореме Пифагора, или с применением тригонометрических зависимостей.
Тогда:
W = mgΔh = mgа(√2 – 1)/2 = 100×10×1×(1,414 — 1)/2 ≈ 207 Дж
Пример решения задачи из раздела кинематика
Автомобиль движется между городами Барнаул и Камень-на-Оби с постоянной скоростью v = 60 км/час.
Определить частоту вращения n колес автомобиля и сколько оборотов nl сделает каждое колесо в течение поездки, если диаметр колеса d = 0,6 м (считать, что колеса автомобиля катятся без пробуксовки) .
Расстояние между городами принять равным l = 180 км.
Для определения числа оборотов каждого колеса по пути следования, надо всю длину маршрута (180 км = 180 000 м) разделить на длину окружности колеса (lк = πd), тогда:
nl = 180 000/πd ≈ 95541 оборотов .
Для определения частоты вращения колеса можно определить время в пути автомобиля между городами
(t = S/v = 3 часа, т. е. 180 минут) и, разделив количество оборотов nl , совершенных колесом в пути на это время, определить число оборотов n колеса за одну минуту.
Получим:
n = 95541/180 ≈ 530 об/мин .
Пример решения задачи из Статики
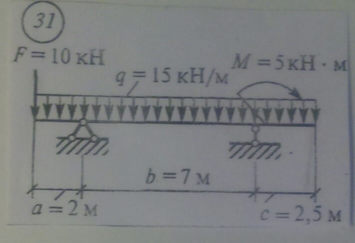
Балка висит на гибких связях горизонтально, нагружена собственным весом G , силой F и находится в состоянии равновесия.
Определить реакцию гибкой связи RА .
Вес балки G = 1200 Н;
Сила F = 600 Н;
Расположение гибких связей и силовых факторов приведено на схеме.
Из условия равновесия балки: сумма моментов всех приложенных к ней сил относительно любой точки балки равна нулю.
Поскольку по условию задания нас интересует лишь реакция RA , то уравнение моментов составляем относительно точки В (момент неизвестной силы RВ относительно этой точки равен нулю) , при этом силы, стремящиеся повернуть балку вокруг точки В по часовой стрелке, мы считаем положительными, против часовой стрелки – отрицательными.
Тогда:
4RA – 2G – F = 0 , откуда: RA = (2G + F)/4 = 750 Н .
Решение задачи из раздела Динамика
Для изображенной на схеме передачи определить вращающий момент Т2 на ведомом валу.
Исходные данные:

Мощность на ведущем валу Р1 = 8 кВт;
Угловая скорость ведущего вала ω1 = 40 рад/сек;
Коэффициент полезного действия передачи η = 0,97;
Передаточное число передачи u = 4.
Сначала определим мощность Р2 на ведомом валу редуктора, с учетом потерь (исходя из величины КПД):
Для определения мощности ведомого вала необходимо знать его угловую скорость ω2 , которая определяется из соотношения u = ω1/ω2, где u = 4 — передаточное число передачи. Получаем: ω2 = ω1/u = 10 рад/сек.
Вращающий момент равен отношению мощности ведомого вала к его угловой скорости:
Задача из раздела динамика
Лебедка состоит из цилиндрической передачи и барабана, к которому посредством троса прикреплен груз G . Определить требуемую мощность Рм электродвигателя лебедки, если скорость подъема груза должна составлять v = 4 м/сек.
Вес груза G = 1000 Н;
Скорость подъема груза v = 4 м/сек;
КПД барабана лебедки ηб = 0,9;
КПД цилиндрической передачи ηц = 0,98;
Элементы конструкции приведены на схеме.
Определим мощность на выходе из привода, необходимую для подъема груза с данной скоростью:
Чтобы найти требуемую мощность электродвигателя для лебедки необходимо определить КПД всей передачи:
ηп = ηб×ηц = 0,9×0,98 = 0,882.
Требуемая мощность электродвигателя:
Рм = Р2 / ηп = 4000/0,882 ≈ 4535 Вт .
Видео:Определение реакций опор в балке. Сопромат.Скачать

Материалы для скачивания
Рейтинг ↑ не забываем
Порядок действий при демонтаже кондиционеров (посмотреть)
Свод правил вентиляции и кондиционирования 2017 год (посмотреть)
Условные обозначения систем вентиляции и кондиционирования (посмотреть)
Требования к пожарной безопастности по вентиляции и кондиционированию (посмотреть).
Видео:определение реакций в стержнях от действия грузовСкачать

Ответы на задачи по технической механике
Если Вы не нашли свой вариант ответа, обращайтесь перейдя по ссылке в группу ВК опубликовав Ваши задачи прям в ленту группы ,по возможности постараемся Вам помочь
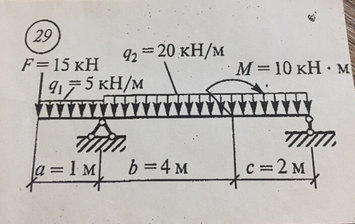
Задача № 29 Найти реакцию опор
Ответ к задачи №29

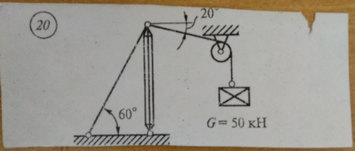
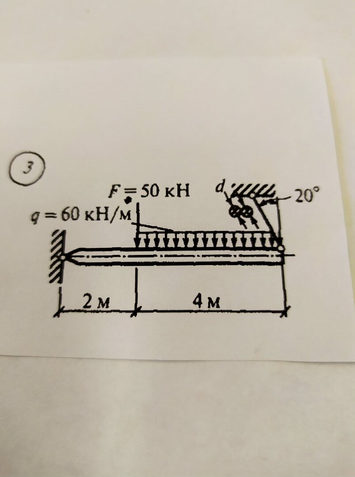
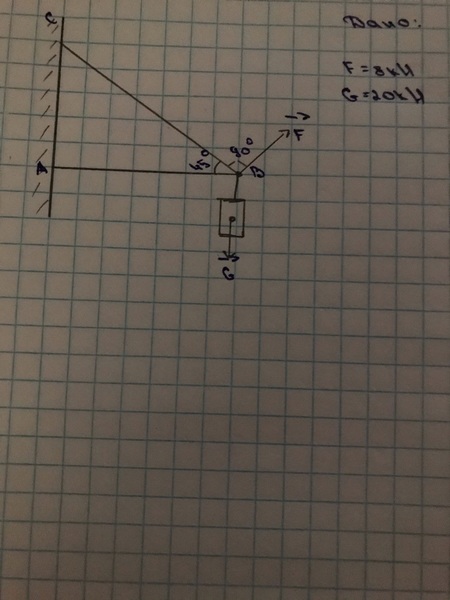
Задача № 20 Натяжка троса
Ответ к задачи № 20
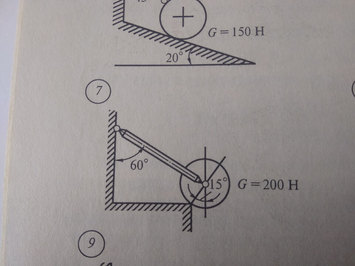
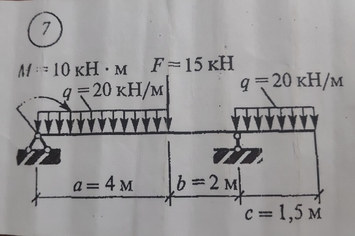
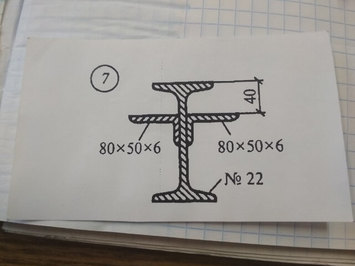
Задача №7 Найти реакцию опор
Ответ к задаче №7
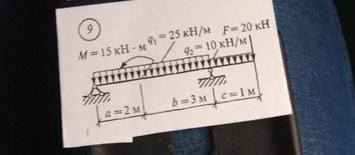
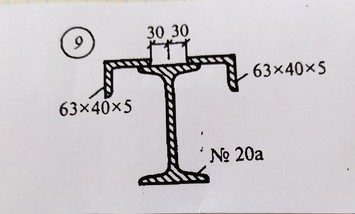
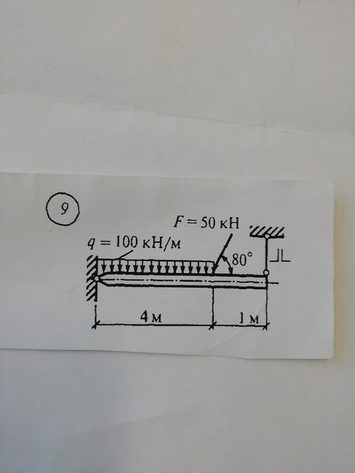
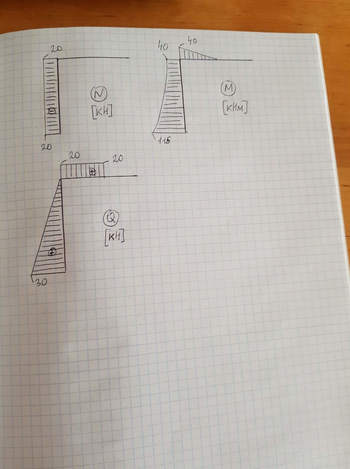
Задача № 9 Распределение нагрузки
Ответ к задачи № 9
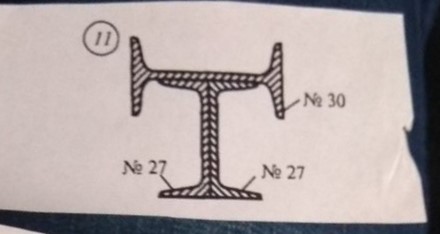
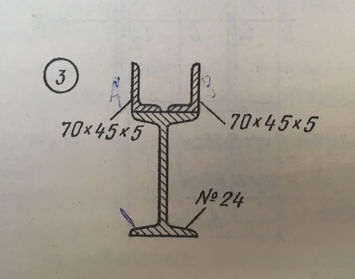
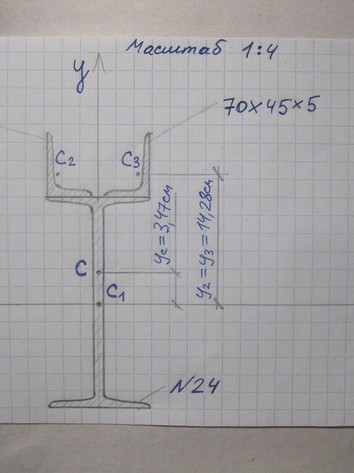
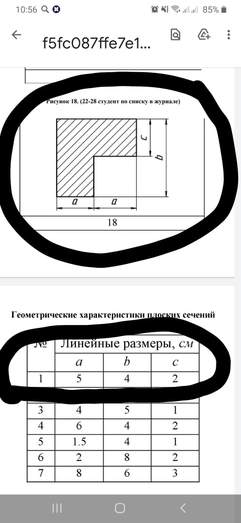
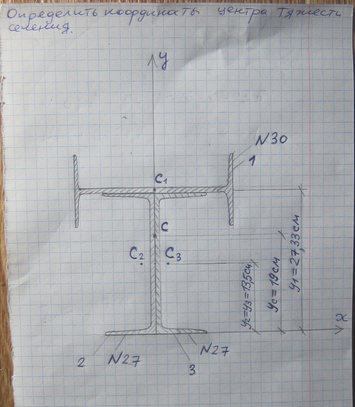
Задача № 11 Определить координаты центра тяжести сечения
Ответ к задачи № 11 С решением
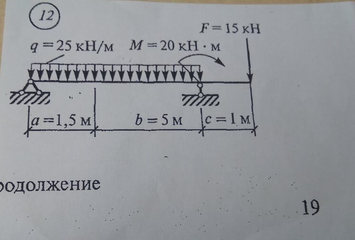
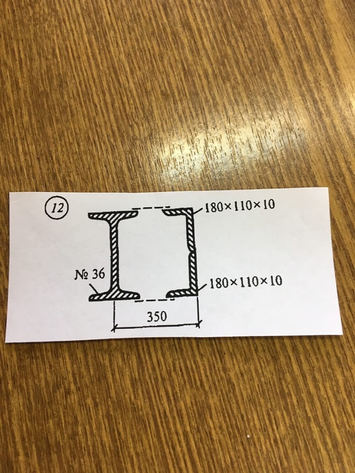
Задача № 12 Найти реакцию опор
Ответ к задачи №12
Задача № 13 Решить графически
Ответ к задаче №13
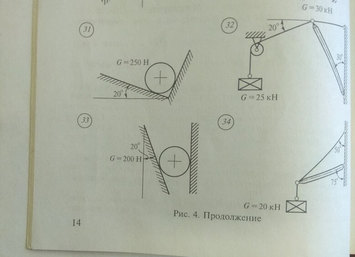
Задача № 33 Решить графически
Ответ к задачи № 33
Задача № 33 Силы давящие на шар
Ответ к задачи № 33 Силы давящие на шар

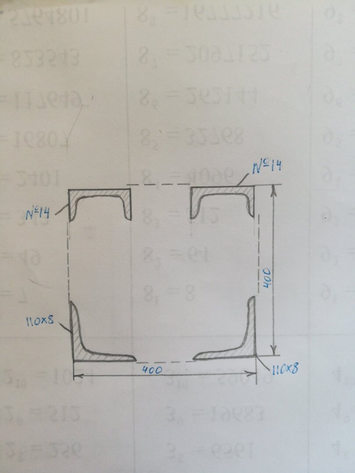
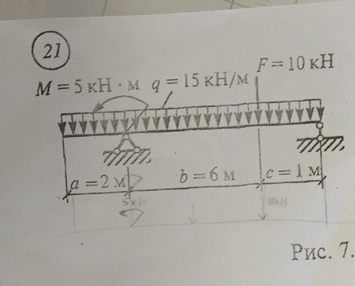
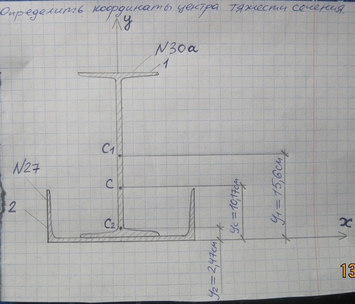
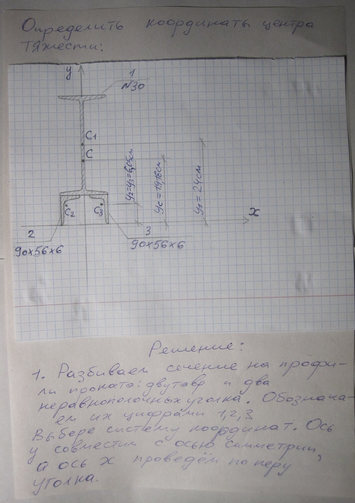
Задача № Задача №21 Определить координат центра тяжести
Ответ к задаче № 21 Определить координат центра тяжести
Ответ № 21 /2 Определить координат центра тяжести 30А Ответ на координат центр тяжести № 21 -27
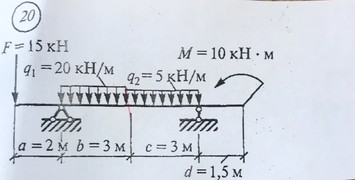
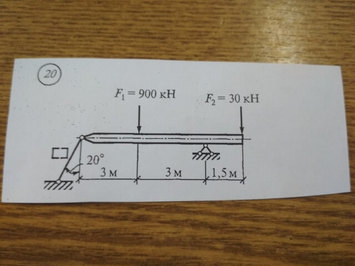
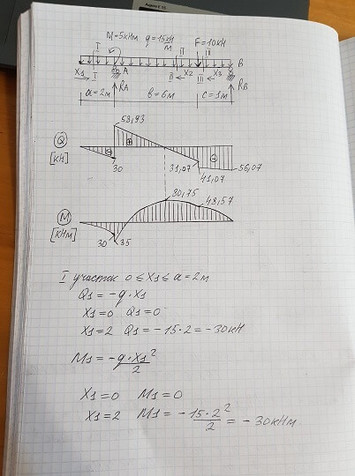
Задача № 20 Определить опорные реакции балки.Проверить правильность их определения
Ответ к задачи № 20 Определить опорные реакции балки.Проверить правильность их определения
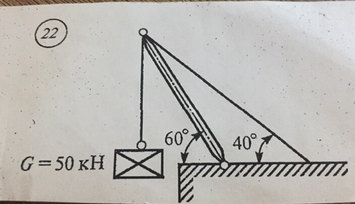
Задача № 22 Задача № 22 найти R(a) и R(b)
Ответ к задачи Задача № 22 найти R(a) и R(b)
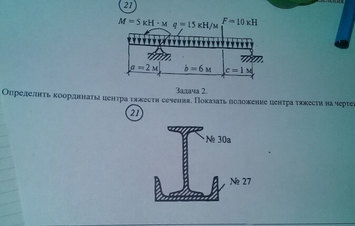
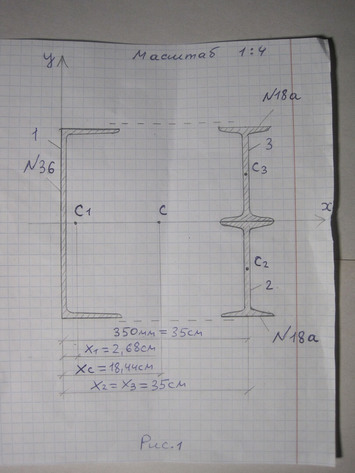
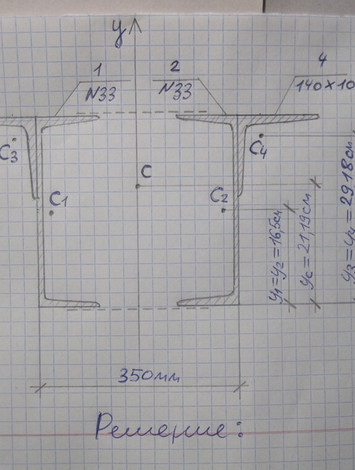
Задача Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
Ответ к задачи Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже

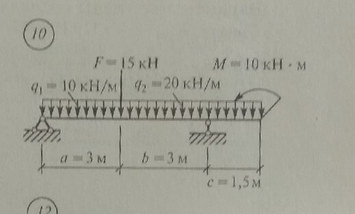
Задача № 10 Найти реакцию опор
Ответ к задачи №10 Найти реакцию опор
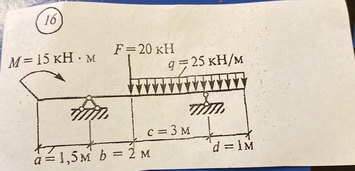
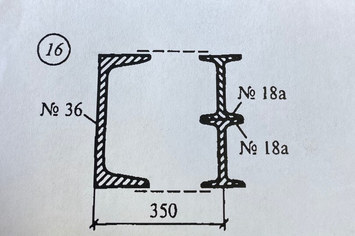
Задача № 16 Определить опорные реакции балки.Проверить правильность их определения
Ответ к задачи № 16
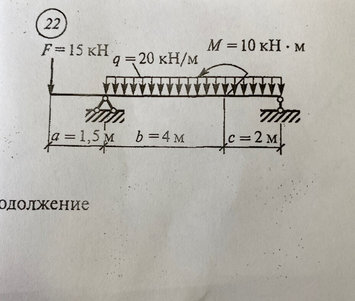
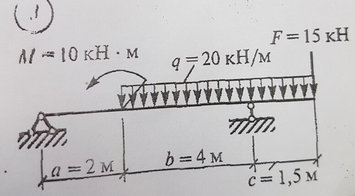
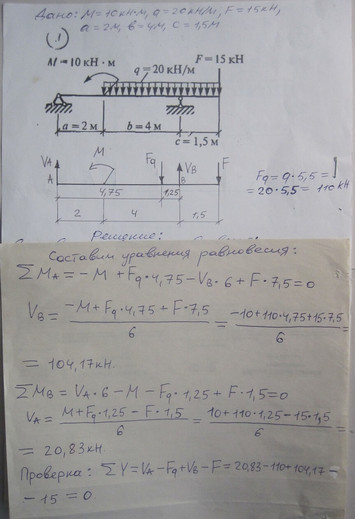
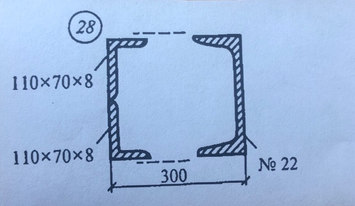
Задача № 22 Определить опорные реакции балки. Проверить правильность их определения
Ответ к задачи № 22 Определить опорные реакции балки Проверить правильность их определения
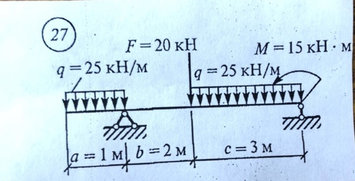
Задача № 27 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 27 Определить опорные реакции балки Проверить правильность их определения
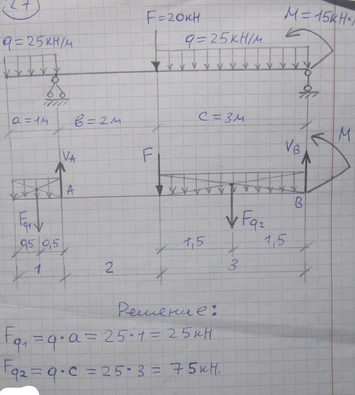
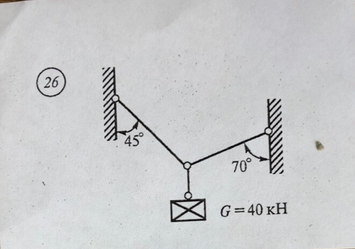
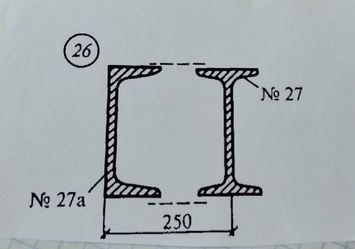
Задача № 26 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 26 Определить опорные реакции балки Проверить правильность их определения
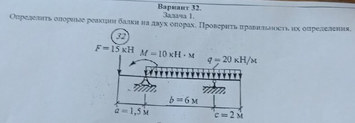
Вариант 32 задача № 1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Ответ к варианту 32 задача №1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
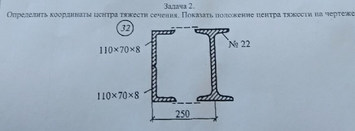
Вариант 32 задача №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Ответ к варианту 32 №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Решение к варианту 32 № 2

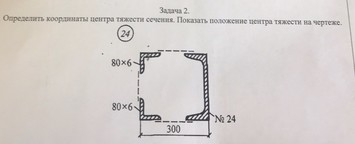
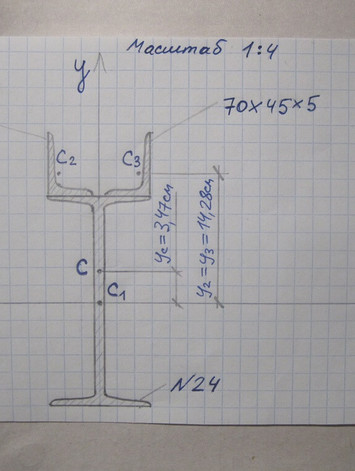
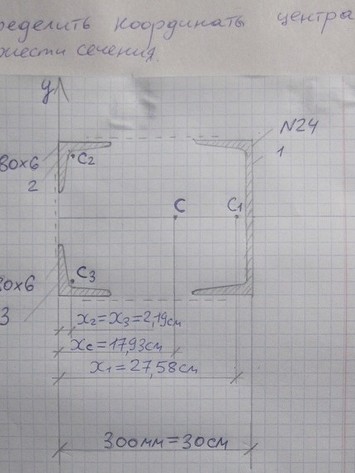
Вариант 24 задача № 2 Определить координаты центра тяжести сечения Показать положения центра тяжести на чертеже
Ответ к варианту 24 задача № 2 Определить координаты центра тяжести сечения
Задача Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
Ответ к задачи Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба

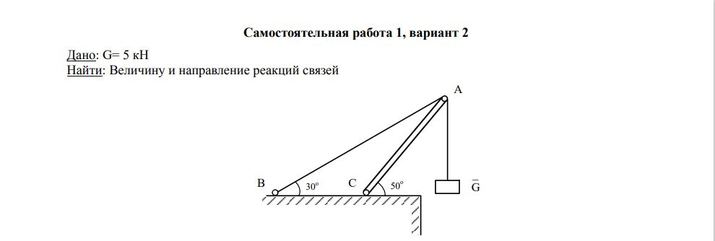
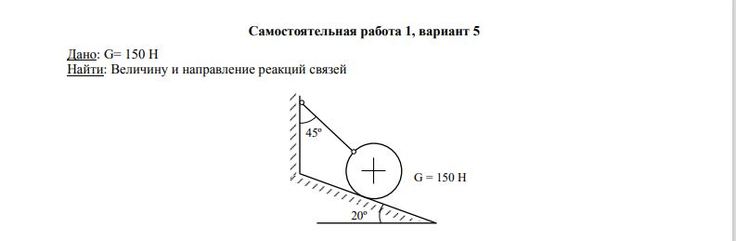
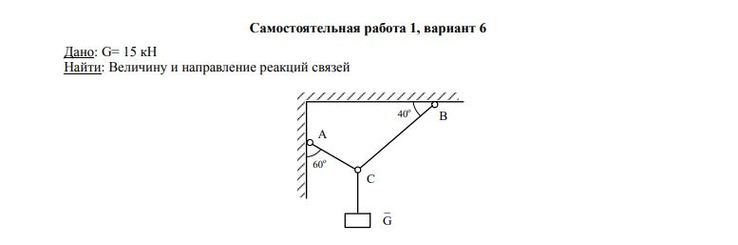
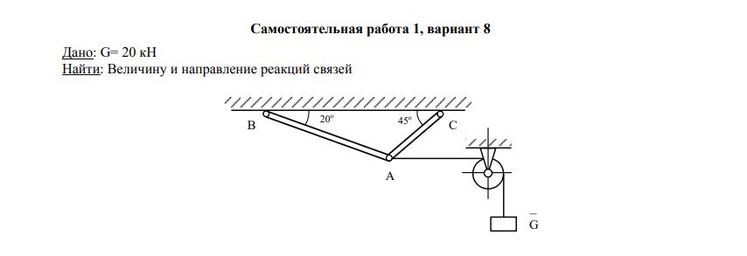
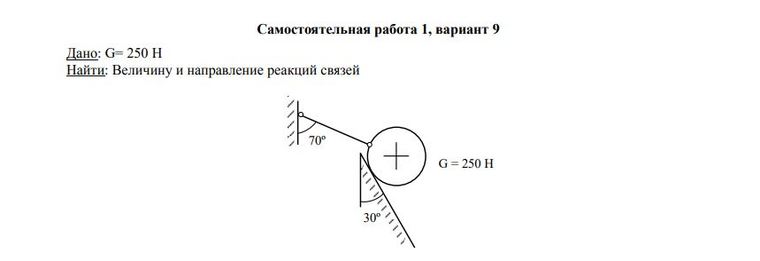
Задача — Определить величину и направления реакцию связей
Ответ к задаче -Определить величину и направления реакций связей
Задача- Определить опорные реакции балки на 2-х опорах
Ответ к задачи Определить опорные реакции балки на 2-х опорах
Задача № 9 Найти центр тяжести
Ответ к задаче № 9 найти центр тяжести

Найти центр тяжести
Решение к задаче Найти центр тяжести
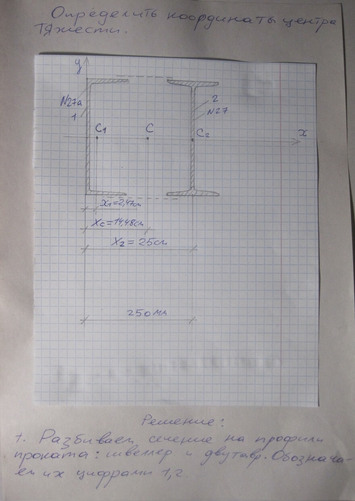
Решение к задаче № 7

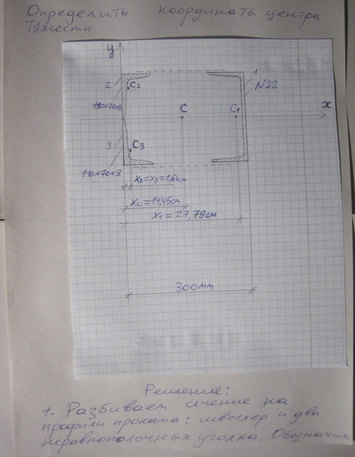
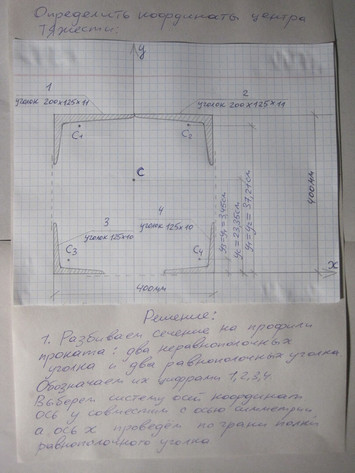
28 задача Определить положение координаты центра тяжести
Ответ к 28 задачи Определить положение координаты центра тяжести






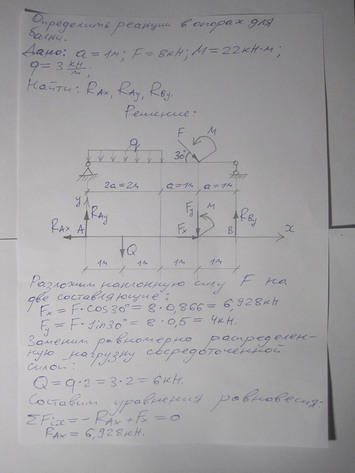

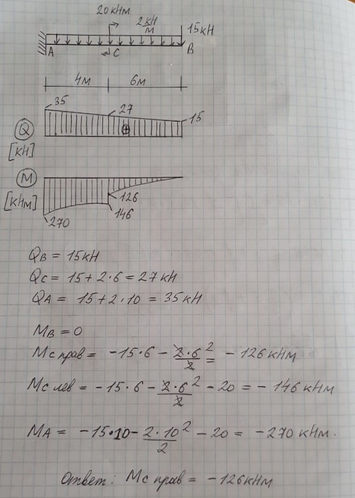

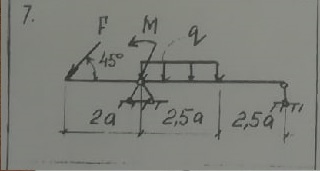

Ответ к задаче — Момент силы относительно точки
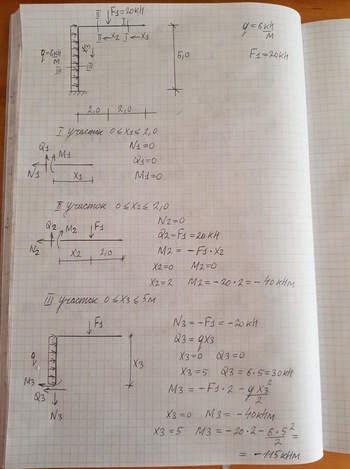
Задача — Понятие о внецентренном растяжении ( сжатии)
Ответ к задаче — Понятие о внецентренном растяжении ( сжатии)
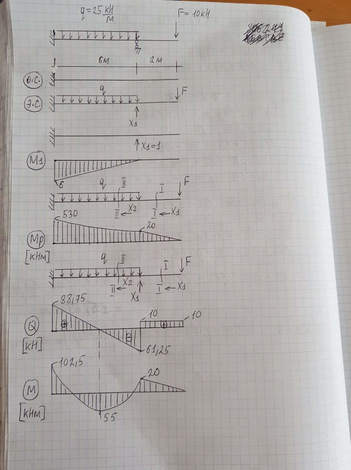
Ответ к заданию для Натальи Добринской

Рисунок Д вариант чисел 1 Задача

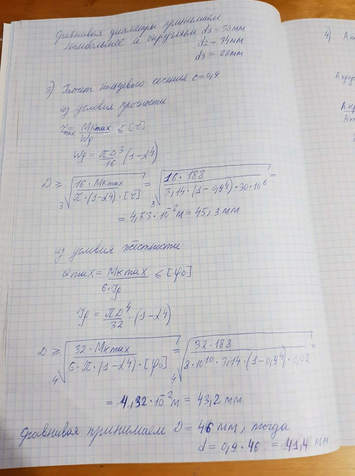
Ответ к задаче ⇑

Ответ к задаче ⇑
Ответ к задаче ⇑
Ответ к задаче ⇑
Полезные материалы
Оконный кондиционер
Mitsubishi MS-GF25/MU-GF25VA — 54700 руб.
Ремонт системы чиллер-фанкойл
Руководства
DAIKIN Ururu Sarara FTXR28E/RXR25E — 71550р.
Мы занимаемся установкой систем вентиляции и кондиционирования в Подольске с 2009 года, затем география наших услуг расширилась до городов Щербинка, Чехов, Серпухов, Домодедово.
Сейчас наши специалисты выезжают в города по всей Московской области. Квалификация подтверждается ежегодно, путём прохождения аттестации в климатических компаниях мировых лидеров.
Полученные знания и навыки позволяют нам найти и решить проблему любой сложности.
Наши цены Вас приятно удивят!
Монтаж кондиционера или вентиляционного оборудования можно заказать по телефонам в Подольске, Чехове, Щербинке и других городах Московской области
О Компании
Климатическая техника сегодня – уже не роскошь, а иногда, это даже потребность и необходимость. Чтобы Ваш дом был полон заботы и комфорта, кондиционер – одна из его немногих составляющих.
Меню опросов
Контакты
Адрес: МО, Г.о. Подольск,
Железнодорожная 2б, офис1
Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Задачи по теоретической механике с подробными решениями
Видео:Как решить любую задачу по механике. АлгоритмСкачать

Подробные решения задач по теоретической механике
Здесь приводятся условия задач по теоретической механике, имеющие подробные решения с ответами. Задачи сгруппированы по основным разделам теоретической механики: статика, кинематика и динамика. Чтобы посмотреть решение, нажмите на соответствующую ссылку в конце условия.
Статика
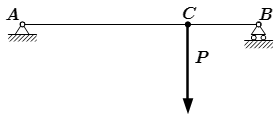
Найти графическим способом реакции опор балки AB , на которую действует сила P , приложенная в точке C .
Дано: P = 55 kH , AB = 10 м , AC = 7 м , BC = 3 м .
Кинематика
Кинематика материальной точки
Определение скорости и ускорения точки по заданным уравнениям ее движения
Дано: Уравнения движения точки: x = 12 sin( πt/ 6) , см; y = 6 cos 2 ( πt/ 6) , см.
Установить вид ее траектории и для момента времени t = 1 с найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
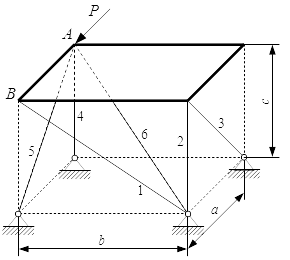
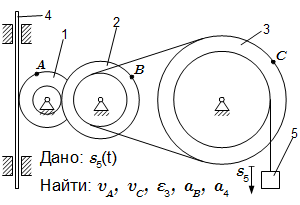
Поступательное и вращательное движение твердого тела
Дано:
t = 2 с; r1 = 2 см, R1 = 4 см; r2 = 6 см, R2 = 8 см; r3 = 12 см, R3 = 16 см; s5 = t 3 – 6t (см).
Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.
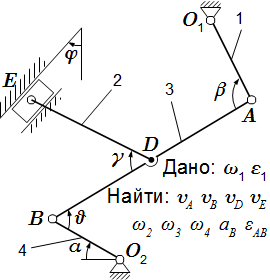
Кинематический анализ плоского механизма
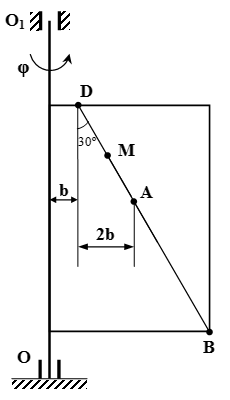
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна E. Стержни соединены с помощью цилиндрических шарниров. Точка D расположена в середине стержня AB.
Дано: ω1, ε1.
Найти: скорости VA, VB, VD и VE; угловые скорости ω2, ω3 и ω4; ускорение aB; угловое ускорение εAB звена AB; положения мгновенных центров скоростей P2 и P3 звеньев 2 и 3 механизма.
Определение абсолютной скорости и абсолютного ускорения точки
Прямоугольная пластина вращается вокруг неподвижной оси по закону φ = 6 t 2 – 3 t 3 . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO 1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость s = AM = 40( t – 2 t 3 ) – 40 ( s — в сантиметрах, t — в секундах). Расстояние b = 20 см . На рисунке точка M показана в положении, при котором s = AM > 0 (при s 0 точка M находится по другую сторону от точки A ).
Найти абсолютную скорость и абсолютное ускорение точки M в момент времени t 1 = 1 с .
Динамика
Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
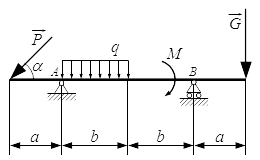
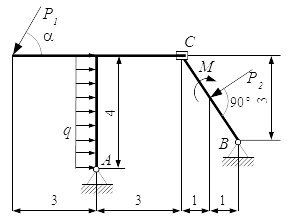
Груз S, рассматриваемый как материальная точка массы m = 5кг, движется по шероховатой поверхности от точки A до точки B, в которой отрывается от поверхности и продолжает движение в воздухе до падения на наклонную поверхность в точке C. Движение происходит в плоскости рисунка.
В точке A, груз имел скорость vA = 1 м/с. Скорость в точке B: vB = 4 м/с. Участок AB представляет собой плоскую поверхность с углом наклона α = 30° к горизонту. На участке AB, кроме силы тяжести и силы трения, на груз действует постоянная сила Q = 10 Н, направленная под углом φ = 45° к поверхности. Коэффициент трения f = 0,1 .
На участке BC, груз движется под действием только силы тяжести. Сопротивлением воздуха пренебречь. Поверхность, на которую падает груз, является плоской с углом наклона β = 15° к горизонту (см. рисунок). Точка D расположена ниже точки B на расстояние |BD| = h = 1 м .
Найти: Время движения tAB на участке AB; длину этого участка; время падения tBC от точки B к точке C; расстояние |DC|; уравнение траектории BC.
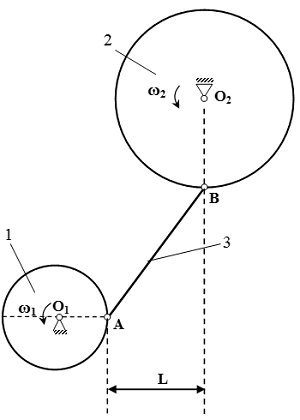
Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
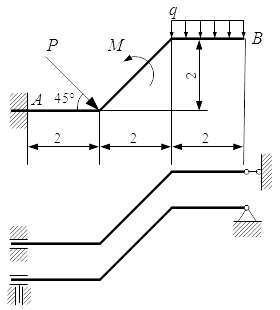
Груз D массой m, получив в точке A начальную скорость V0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости. На участке AB, длина которого l, на груз действует постоянная сила T(ее направление показано на рисунке) и сила R сопротивления среды (модуль этой силы R = μV 2 , вектор R направлен противоположно скорости V груза).
Груз, закончив движение на участке AB, в точке B трубы, не изменяя значения модуля своей скорости, переходит на участок BC. На участке BC на груз действует переменная сила F, проекция Fx которой на ось x задана.
Считая груз материальной точкой, найти закон его движения на участке BC, т.е. x = f(t), где x = BD. Трением груза о трубу пренебречь.
Теорема об изменении кинетической энергии механической системы
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3, блока 4 и подвижного блока 5. Заданы радиусы ступеней и радиусы инерции шкива 3 и блока 4. Блок 5 считать сплошным однородным цилиндром. Коэффициент трения груза 2 о плоскость f = 0,1 . Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3. Участки нитей параллельны соответствующим плоскостям. К подвижному блоку 5 прикреплена пружина с коэффициентом жесткости с .
Под действием силы F = f ( s ) , зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя. Деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент M сил сопротивления (от трения в подшипниках).
Заданы массы тел m 1 , m 2 , m 3 , m 4 , m 5 , коэффициент жесткости пружины c , зависимость силы от перемещения F = f ( s ) , величина момента M .
Определить значение центра масс тела 5 VC 5 в тот момент времени, когда перемещение s груза 1 станет равным s 1 = 0,2 м .
Применение общего уравнения динамики к исследованию движения механической системы
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м , приложенной к шкиву 1. Заданы радиусы ступеней шкивов, их радиусы инерции относительно осей вращения, а также веса шкивов и грузов. Грузы, веса которых равны нулю, на чертеже не изображать.
Пренебрегая трением, определить ускорение груза 5 .
Применение принципа Даламбера к определению реакций опор вращающегося тела
Вертикальный вал AK, вращающийся равномерно с угловой скоростью ω = 10 с -1 , закреплен подпятником в точке A и цилиндрическим подшипником в точке D.
К валу жестко прикреплены невесомый стержень 1 длиной l1 = 0,3 м, на свободном конце которого расположен груз массой m1 = 4 кг, и однородный стержень 2 длиной l2 = 0,6 м, имеющий массу m2 = 8 кг. Оба стержня лежат в одной вертикальной плоскости. Точки прикрепления стержней к валу, а также углы α и β указаны в таблице. Размеры AB=BD=DE=EK=b, где b = 0,4 м. Груз принять за материальную точку.
Пренебрегая массой вала, определить реакции подпятника и подшипника.
🌟 Видео
Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Задача о составной конструкцииСкачать

Техническая механика/Определение реакций в жесткой заделке.Скачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Определение реакций опор простой рамыСкачать

Как чжанчжуан лечит?Скачать

Определение опорных реакций в простой балке. Урок №1Скачать
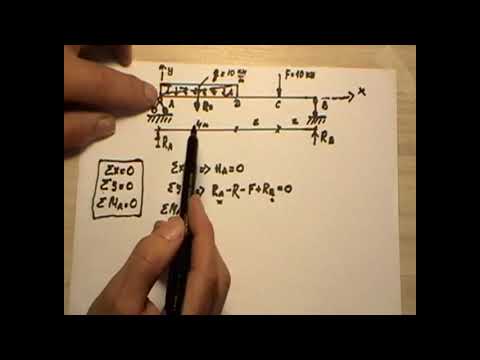
Определение опорных реакций в заделке консольной балкиСкачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Математика это не ИсламСкачать