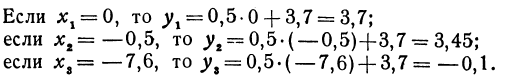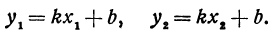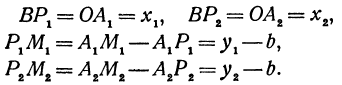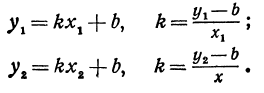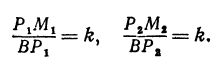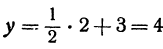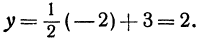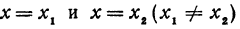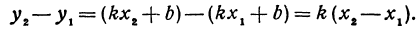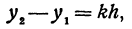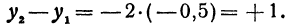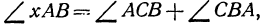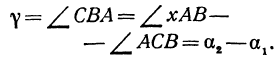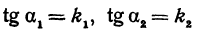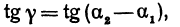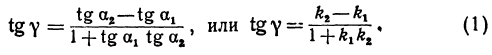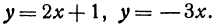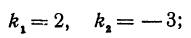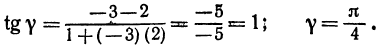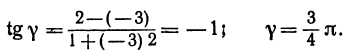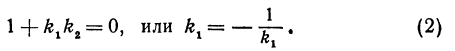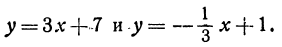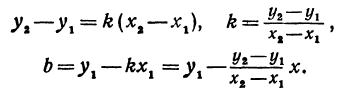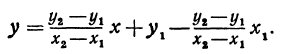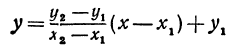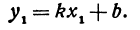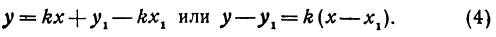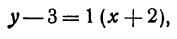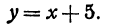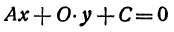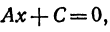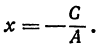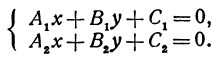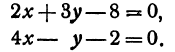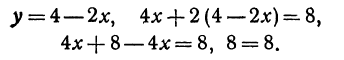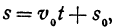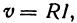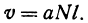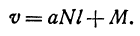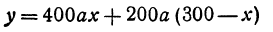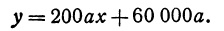О чем эта статья:
- Понятие функции
- Понятие линейной функции
- Свойства линейной функции
- Построение линейной функции
- Решение задач на линейную функцию
- Функция y=k/х — свойства, график и примеры решения задач
- Общие сведения
- Прямоугольная система координат
- Линейная функция в математике с примерами решения и образцами выполнения
- Определение и геометрический смысл
- Основное свойство линейной функции
- Задачи на прямую
- Общее уравнение прямой. Неявная линейная функция
- Система двух уравнений первой степени
- Примеры решения линейной функции
- Примеры применения линейной функции
- 🎥 Видео
Видео:Занятие 1. График линейной функции y=kx+bСкачать

Понятие функции
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 0 | 2 | 4 |
| y | -2 | -1 | 0 |
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Видео:ГРАФИК ФУНКЦИИ y = kx + b | линейная функция | 7 классСкачать

Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Видео:Алгебра 7 Линейная функция y=kxСкачать

Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Если k > 0 и b
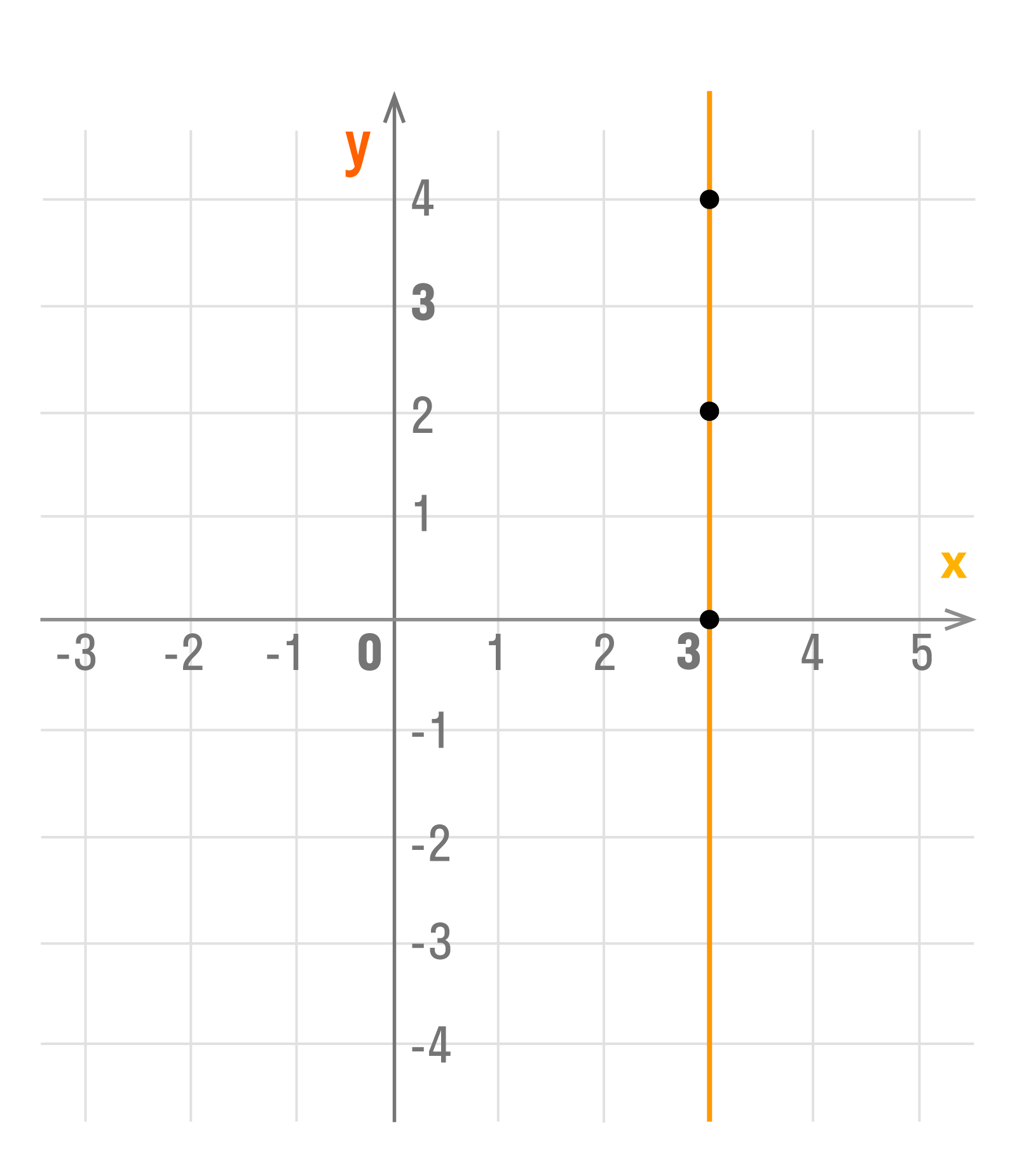
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Видео:Линейная функция и ее график. 7 класс.Скачать

Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
Видео:Алгебра 8 класс (Урок№14 - Функция y = k/x и её график.)Скачать

Функция y=k/х — свойства, график и примеры решения задач
Видео:Функция y=k/x и ее график. 7 класс.Скачать

Общие сведения
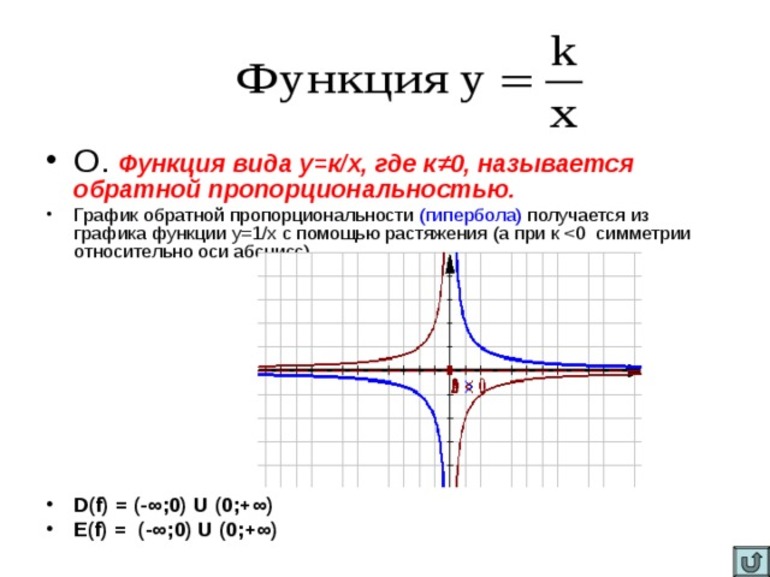
Функцией называется некоторая зависимость переменных друг от друга. В некоторых случаях неизвестные величины могут быть выражены системой конкретных значений, интервалами, а также другими функциональными выражениями. Последний класс называется сложным или составным. Различают зависимые и независимые переменные (аргументы). Второй тип может принимать любые значения, кроме тех, которые превращают выражение в неопределенность.
Однако аргументы необходимо также обследовать, поскольку они могут обратить тождество в пустое множество. Одним из таких примеров является функция у = к / х. Ее аргумент x может принимать любые значения, кроме 0. Именно это число превращает уравнение в неопределенность, поскольку в математике существует следующее правило: запрещается делить на 0.
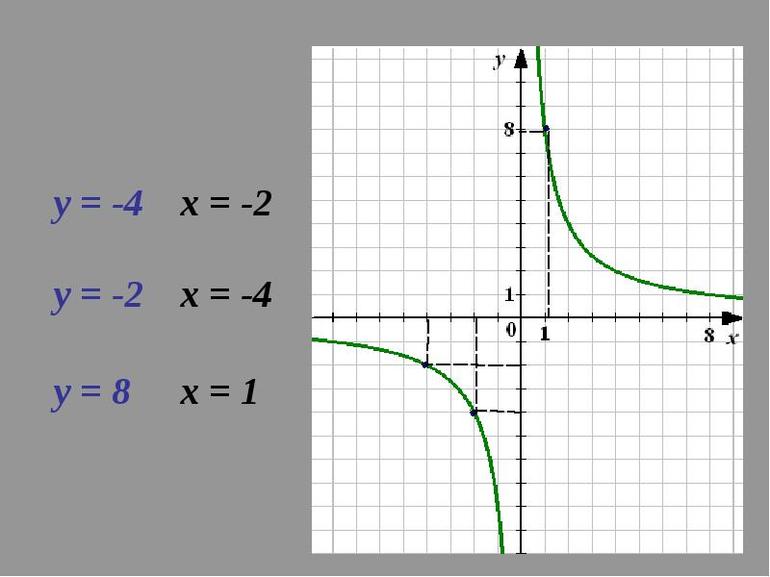
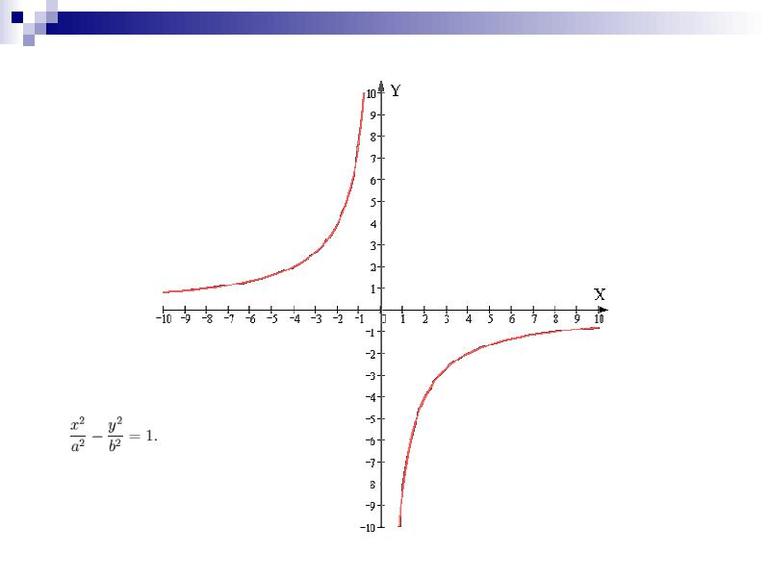
Следует отметить, что существует функция y = k/x и ее график — кривая, имеющая название гипербола. Многие путают его с параболой (в степени 2). Однако она является квадратичной. График строится в системе координат, которая называется декартовой. Кроме того, в математике встречается еще одно уравнение вида y = кх. Ее графиком является прямая.
Прямоугольная система координат
В математике существуют специальные инструменты для построения графиков функций. Одним из них считается распространенная прямоугольная система координат. Она может быть на плоскости и в пространстве. Поскольку y = k/x и y = kx являются элементарными, то для иллюстрации их графиков используется однородная прямоугольная декартовая система координат (рис. 1), элементом которой является точка.
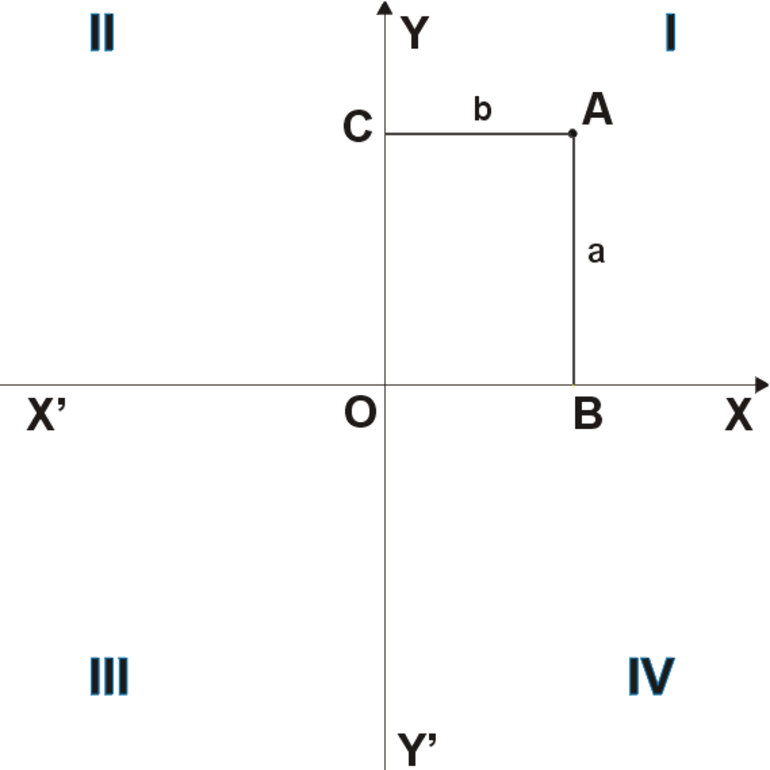
Для декартовой системы на плоскости имеется только две координаты: по взаимно перпендикулярным осям ординат (ОУ) и абсцисс (ОХ). Они пересекаются в некоторой точке О, которая называется началом координат.
Рисунок 1. Прямоугольная декартова система координат (ДСК).
При указании координат нужно учитывать четверть. От нее зависит знак. Оси ординат (игрек) и абсцисс (икс) делят систему на четыре четверти. Они обозначаются римскими цифрами (рис. 1) и имеют такие свойства:
- Первая — I: координаты x и y являются положительными числами, т. е. x > 0 и y > 0.
- II: x 0.
- III: x 0 и y 0, то он является острым, т. е. его значение меньше 90 градусов. При к 0, то она располагается в I и III. Когда к 0 при х, принадлежащим промежутку (2;6) U [8;10]. Аналогично указывается отрезок, на котором заданная функция принимает отрицательные значения (f(x) 0). Следовательно, она обладает такими свойствами:
- График: кривая-гипербола.
- D(y) = (-inf;0) U (0;+inf).
- Если x > 0, то y > 0.
- При отрицательных величинах аргумента функция принимает отрицательные значения.
- Она убывает на интервалах: (-inf;0) и (0;+inf).
- Точек экстремума нет.
- Непрерывна, кроме точки х = 0.
- Непериодическая.
- Нечетная.
Когда к 0 при отрицательных значениях аргумента, а y 0. Функция y = kx обладает такими свойствами (k > 0):
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Линейная функция в математике с примерами решения и образцами выполнения
Линейная функция — функция вида y=kx+b (для функций одной переменной).
Видео:Линейная функция и ее график. 7 класс.Скачать

Определение и геометрический смысл
Рассмотрим уравнение с двумя неизвестными х и у:
где 
удовлетворяют следующие пары:
Для того чтобы найти пару чисел, удовлетворяющих уравнению ( * ), нужно придать х произвольное числовое значение и подставить в уравнение ( * ), тогда у получит определенное числовое значение. Например, если х = 27, то у = 2 x 27 — 6 = 48. Очевидно, что пара чисел х =27 и у =48 удовлетворяет уравнению (*). Так же и в случае уравнения (1) можно придать х произвольное числовое значение и получить для у соответствующее числовое значение.
Так как в данном уравнении х может принимать любое числовое значение, то его называют переменной величиной. Поскольку выбор этого числового значения ничем не ограничен, то х называют независимой переменной величиной или аргументом.
Для у получаются также различные значения, но уже в зависимости от выбранного значения х; поэтому у называют зависимым переменным или функцией.
Функцию у, определяемую уравнением (1), называют линейной функцией.
Пример:
Вычислить значения линейной функции, определяемой уравнением у = 0,5х + 3,7, при следующих значениях независимого переменного: х1 = 0, х2 = —0,5, х3 = —7,6.
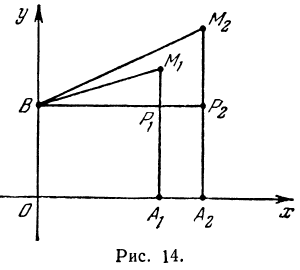
Покажем, что если принять пару чисел х и у, удовлетворяющих уравнению (1), за абсциссу и ординату точки, то геометрическим местом этих точек будет прямая линия (рис. 14).
В самом деле, рассмотрим точку В(0, b) и точки М1(х1, у1) и М2(х2, у2), координаты которых удовлетворяют уравнению (1), т. е.
Обозначим проекции точек М1 и М2 на ось Ох через А1 и A2, тогда ОА1 = х1, ОА2 = х2, А1М1= у1, А2М2 = у2. Проведем из точки В прямую, параллельную оси Ох. При этом получим b = ОВ = А1Р1 = А2Р2.
Предположим, что точки BМ1 и М2 не лежат народной прямой. Соединяя точку В с точками М1 и М2, получим два прямоугольных треугольника ВР1М1 и ВР2М2, из которых имеем:
Но так как х1, у1 и х2, у2 удовлетворяют уравнению (1), то
Выражения 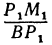
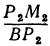








Так как М1 и М2 — произвольные точки, координаты которых удовлетворяют уравнению (1), то можно сделать следующее заключение: любая точка, координаты которой удовлетворяют уравнению (1), лежит на прямой, отсекающей на оси Оу отрезок ОВ = b и образующей с положительным направлением оси Ох угол а такой, что tg a = 
Число b называется начальной ординатой, число 
Предыдущие рассуждения позволяют сделать вывод: линейная функция y = 

Например, линейная функция 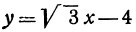
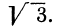
Если имеем определенную прямую, отсекающую на оси Оу отрезок b и наклоненную к оси Ох под углом 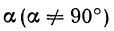
Очевидно, имеет место и такое предложение:
Всякой прямой, отсекающей на оси Оу отрезок b и наклоненной к оси Ох под углом, тангенс которого равен числу 

Координаты любой тонки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение у = 
Отметим частные случаи.
1.Пусть b = 0, т. е. линейная функция определяется уравнением
Прямая, определяемая этим уравнением, проходит через начало координат. Здесь у пропорционален х, т. е. если х увеличить (уменьшить) в несколько раз, то и у увеличится (уменьшится) во столько же раз.
2.Пусть 
Этому уравнению соответствует прямая, параллельная оси Ох и отстоящая от нее на расстояние b.
На основании всего сказанного в этом параграфе легко решаются следующие задачи.
Задача:
Даны точки А (3, 5) и В(— 1, 4). Нужно узнать, лежат ли эти точки на прямой, уравнение которой имеет вид
Решение:
Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки А в уравнение (*), получим 5 = 2 x 3 — 1. Это тождество, следовательно, точка А лежит на прямой. Подставляя координаты точки В, получаем 4 = 2(— 1)—1 = —3. Отсюда видно, что точка В не лежит на прямой.
Задача:
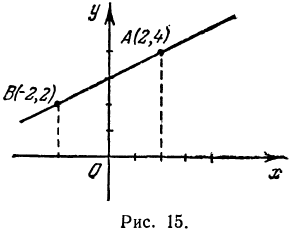
Построить прямую, уравнение которой
Решение:
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим х произвольное значение, например х = 2, и найдем из уравнения (**) значение
Значит, точка A (2, 4) лежит на прямой.
Это первая точка. Теперь дадим х какое-нибудь другое значение, например х = —2, и вычислим у из уравнения (**).
Точка B ( — 2, 2) лежит на прямой. Это вторая точка. Строим точки A и B (рис. 15) и проводим через них прямую, это и есть искомая прямая.
Видео:функция y=k/x и ее график (гипербола) - 8 класс алгебраСкачать

Основное свойство линейной функции
Рассмотрим линейную функцию у = 
Здесь первое и второе значения х различны, они отличаются друг от друга на величину х2 — х1. Величину разности х2 — х1, на которую изменяется x при переходе от x1 к х2, назовем приращением независимого переменного х. Эту величину часто будем обозначать через h, так что h = x2 — x1. Найдем, насколько изменилось значение у при изменении х1 на h . Для этого вычтем из у2 значение у1
т. е. приращение линейной функции пропорционально приращению независимого переменного.
Это и есть основное свойство линейной функции. Заметим, что х2 может быть больше, а может быть и меньше, чем х1. Поэтому h = x2 — x1 может быть как положительным, так и отрицательным числом, иначе говоря, приращение h независимого переменного может быть любого знака. То же самое относится и к приращению функции, т. е. к величине у2—у1.
Пример:
Найдем приращение функции y = 0,6x—3, если приращение независимого переменного h = 0,1.
По основному свойству у2—у1 = 0,6 x 0,1 = 0,06.
Приращение этой же функции y = 0,6x—3 , если h = —3, будет равно у2—у1 = 0,6 x (— 3) = —1,8. В этом случае приращения независимого переменного и функции отрицательны, т. е. в этом случае и независимое переменное и функция не увеличиваются, а уменьшаются.
Пример:
Найдем приращение функции у = —2x+10 при изменении х на h = —0,5. Будем иметь
Видео:Вариант 51, № 7. Нахождение k и b линейной функции y=kx+b. Пример 1Скачать

Задачи на прямую
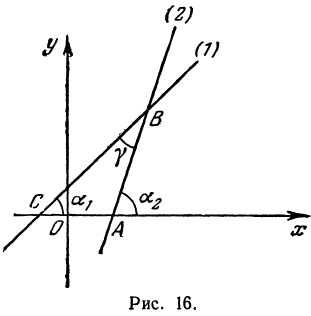
Задача:
Найти угол y между двумя прямыми, заданными уравнениями
Решение:
При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).
Угол хАВ является внешним по отношению к треугольнику ABC, поэтому он равен сумме двух внутренних углов треугольника, с ним не смежных, т. е.
Но углы а1 и а2 непосредственно неизвестны, а известны их тангенсы
Пример:
Найти угол между прямыми, заданными уравнениями
применяя формулу (1), получим;
Если же будем считать, что
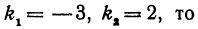
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.
Если заданы две параллельные прямые, то углы а1 и а2 равны, как соответственные, следовательно, тангенсы их тоже равны
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.
Если прямые перпендикулярны, то угол между ними равен 90°, т. е. 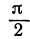
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример:
Найдем угол между прямыми, заданными уравнениями
Здесь угловые коэффициенты (первый равен 3, а второй 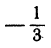
Задача:
Даны две точки: M1(x1, у1) и М2(х2, у2), где 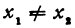
Решение:
Искомая прямая не параллельна оси Оу, поэтому ее уравнение можно написать в виде 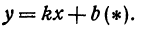

Так как прямая проходит через точки М1 и М2, то координаты этих точек должны удовлетворять уравнению ( * ), т. е.
В уравнениях ( ** ) и (*** ) все числа, кроме 

Подставляя найденные выражения в уравнение (*), получим
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси Оу.
Полученному уравнению можно придать форму, удобную для запоминания, а именно:
Задача:
Написать уравнение прямой, проходящей через данную точку М(х1,у1) и образующей с осью Ох угол а.
Решение:
Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла а. Обозначим 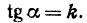
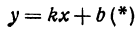
Находим отсюда неизвестное b, получим 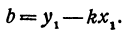
Это и есть уравнение прямой, проходящей через точку М в заданном направлении.
Если в уравнении (4) менять направление, не меняя точку M, то получим уравнение всех прямых, проходящих через заданную точку. Уравнение 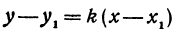

Пример:
Напишем уравнение прямой, проходящей через точку М( — 2, 3) и образующей с осью Ох угол 45°.
Так как tg 45° = 1, то угловой коэффициент равен 1; х1 = —2; у1 = 3. Уравнение прямой запишется в виде
Видео:Алгебра 8 класс (Урок№3 - График функции y=kx)Скачать

Общее уравнение прямой. Неявная линейная функция
Рассмотрим уравнение первой степени с двумя неизвестными
Решим его относительно у:
т. е. мы получили линейную функцию, где 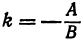
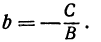
Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой.
Рассмотрим особо случай, когда B = 0, так как на нуль делить нельзя.
Уравнение (1) примет вид
Поэтому, каков бы ни был у, х всегда равен 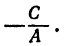
Таким образом, любому уравнению первой степени соответствует некоторая прямая. Придавая в уравнении (1) коэффициентам А, В и С различные значения, можно получить любое уравнение первой степени. Поэтому уравнение (1) называют общим уравнением прямой.
Из уравнения (1) (если 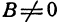
Видео:Алгебра 7 класс. 8 октября. y=kxСкачать

Система двух уравнений первой степени
Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке).
Рассмотрим систему двух уравнений
Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения х и у, которые удовлетворяют и первому и второму уравнениям. Но так как х и у определяют точку, то следовательно, решить систему—это значит найти точку, лежащую и на первой и на второй прямых, т. е. найти точку пересечения прямых.
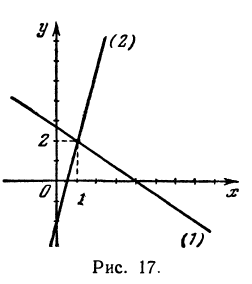
Пример:
Найдем точку пересечения двух прямых:
Решая эту систему, получим: х = 1, у = 2, т. е. прямые пересекаются в точке (1,2) (рис. 17).
Пример:
Найдем точку пересечения двух прямых:
Решая эту систему, получим:
Последнее равенство нелепо, значит, прямые не пересекаются, Рис. 17. т. е. они параллельны.
Пример:
Найдем точку пересечения данных прямых
Решая эту систему, получим:
Полученное равенство всегда справедливо, т. е. справедливо при любом значении x. Это значит, что две прямые пересекаются в каждой своей точке, что может быть только тогда, когда они сливаются.
Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.
Видео:Построение графика линейной функции y=kx+bСкачать

Примеры решения линейной функции
Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.
Пример:
Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения
где — начальное расстояние, v0 — скорость, t — время; это, как мы уже знаем, есть линейная функция.
Пример:
Закон Ома записывается в виде
где v — напряжение, R — сопротивление и I — ток. Если не изменяется, то v является линейной функцией тока I .
Пример:
Если стоимость провоза единицы товара по железной дороге равна а руб. за километр, то стоимость v провоза N единиц товара на l км равна
Если же стоимость товара на месте равна М руб., то после перевозки за него надо заплатить
Здесь v—линейная функция l.
Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.
Задача:
Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А и В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В—200 т. Перевозка одной тонны нефти на один километр обходится в а руб.
Решение:
Обозначим расстояние от А до предполагаемого пункта С через х. Тогда расстояние от города В до С равно 300 — х. Стоимость перевозки одной тонны нефти из С в A равна ах руб., а перевозки 400 т—400аx руб. Аналогично перевозка нефти из С в В будет стоить 200а (300 — х) руб. Стоимость всех перевозок, которую обозначим через у, будет выражаться так:
Это линейная функция. Если примем х за абсциссу, а у за ординату точки, то полученная линейная функция определяет уравнение некоторой прямой. Угловой коэффициент ее равен 200а, т. е. положителен, следовательно, эта прямая образует с осью Ох острый угол и поэтому с увеличением независимого переменного поднимается вверх. По смыслу задачи величина х заключена между 0 и 300, т. е. 
Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе A, если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к A, тем выгодней.
Видео:ЛИНЕЙНАЯ ФУНКЦИЯ | 7 класс Макарычев | график функции y=kx+bСкачать

Примеры применения линейной функции




Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎥 Видео
Линейная функция и её график. Алгебра, 7 классСкачать

Линейная Функция — как БЫСТРО построить график и получить 5-куСкачать

ЛИНЕЙНАЯ ФУНКЦИЯ y=kx график линейной функции 7 и 8 классСкачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Задание 5 Знаки коэффициентов k и b в формуле линейной функции y=kx+bСкачать