При вычислении определенного интеграла не всегда получаем точное решение. Не всегда удается представление в виде элементарной функции. Формула Ньютона-Лейбница не подходит для вычисления, поэтому необходимо использовать методы численного интегрирования. Такой метод позволяет получать данные с высокой точностью. Метод Симпсона является таковым.
Для этого необходимо дать графическое представление выведению формулы. Далее идет запись оценки абсолютной погрешности при помощи метода Симпсона. В заключении произведем сравнение трех методов: Симпсона, прямоугольников, трапеций.
- Метод парабол – суть, формула, оценка, погрешности, иллюстрации
- Суть метода парабол
- Вывод формулы метода Симпсона (парабол)
- Примеры приближенного вычисления определенных интегралов методом парабол
- Замечание
- Метод Симпсона
- Вывод формулы Симпсона
- Готовые работы на аналогичную тему
- Оценка погрешности при использовании метода парабол
- Правило Симпсона: формула, доказательство, примеры, упражнения
- Содержание:
- Формула
- Демонстрация
- Коэффициенты интерполяционного полинома
- Вычисление приближенного интеграла в [Xi, Xi + 2]
- Приближенное вычисление интеграла в [a, b]
- Ошибка приближения
- Примеры работы
- — Пример 1
- Решение
- — Пример 2
- Решение
- — Пример 3
- Решение
- Предлагаемое упражнение
Видео:Метод СимпсонаСкачать
Метод парабол – суть, формула, оценка, погрешности, иллюстрации
Задана функция вида y = f ( x ) , имеющая непрерывность на интервале [ a ; b ] , необходимо произвести вычисление определенного интеграла ∫ a b f ( x ) d x
Необходимо разбить отрезок [ a ; b ] на n отрезков вида x 2 i — 2 ; x 2 i , i = 1 , 2 , . . . , n с длиной 2 h = b — a n и точками a = x 0 x 2 x 4 . . . x 2 π — 2 x 2 π = b . Тогда точки x 2 i — 1 , i = 1 , 2 , . . . , n считаются серединами отрезков x 2 i — 2 ; x 2 i , i = 1 , 2 , . . . , n . Данный случай показывает, что определение узлов производится через x i = a + i · h , i = 0 , 1 , . . . , 2 n .
Видео:Формула СимпсонаСкачать
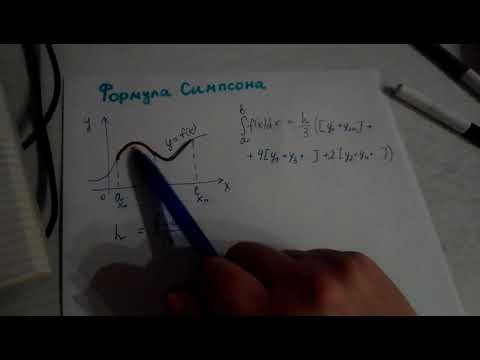
Суть метода парабол
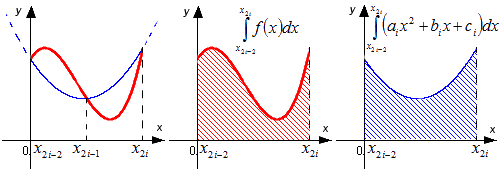
Каждый интервал x 2 i — 2 ; x 2 i , i = 1 , 2 , . . . , n подынтегральной функции приближен при помощи параболы, заданной y = a i x 2 + b i x + c i , проходящей через точки с координатами x 2 i — 2 ; f ( x 2 i — 2 ) , x 2 i — 1 ; x 2 i — 1 , x 2 i ; f ( x 2 i ) . Поэтому метод и имеет такое название.
Данные действия выполняются для того, чтобы интеграл ∫ x 2 i — 2 x 2 i a i x 2 + b i x + c i d x взять в качестве приближенного значения ∫ x 2 i — 2 x 2 i f ( x ) d x . Можем вычислить при помощи формулы Ньютона-Лейбница. Это и есть суть метода парабол. Рассмотрим рисунок, приведенный ниже.
Графическая иллюстрация метода парабол (Симпсона)
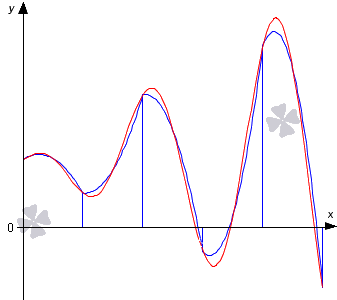
При помощи красной линии изображается график функции y = f ( x ) , синей – приближение графика y = f ( x ) при помощи квадратичных парабол.
Видео:Формула СимпсонаСкачать

Вывод формулы метода Симпсона (парабол)
Исходя из пятого свойства определенного интеграла получаем ∫ a b f ( x ) d x = ∑ i = 1 n ∫ x 2 i — 2 x 2 i f ( x ) d x ≈ ∑ i = 1 n ∫ x 2 i — 2 x 2 i ( a i x 2 + b i x + c i ) d x
Для того чтобы получить формулу методом парабол, необходимо произвести вычисление:
∫ x 2 i — 2 x 2 i ( a i x 2 + b i x + c i ) d x
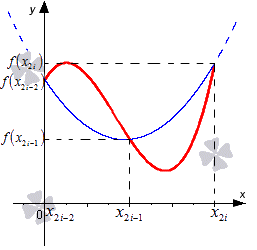
Пусть x 2 i — 2 = 0 . Рассмотрим рисунок, приведенный ниже.
Изобразим, что через точки с координатами x 2 i — 2 ; f ( x 2 i — 2 ) , x 2 i — 1 ; x 2 i — 1 , x 2 i ; f ( x 2 i ) может проходить одна квадратичная парабола вида y = a i x 2 + b i x + c i . Иначе говоря, необходимо доказать, что коэффициенты могут определяться только единственным способом.
Имеем, что x 2 i — 2 ; f ( x 2 i — 2 ) , x 2 i — 1 ; x 2 i — 1 , x 2 i ; f ( x 2 i ) являются точками параболы, тогда каждое из представленных уравнений является справедливым. Получаем, что
a i ( x 2 i — 2 ) 2 + b i · x 2 i — 2 + c i = f ( x 2 i — 2 ) a i ( x 2 i — 1 ) 2 + b i · x 2 i — 1 + c i = f ( x 2 i — 1 ) a i ( x 2 i ) 2 + b i · x 2 i + c i = f ( x 2 i )
Полученная система разрешается относительно a i , b i , c i , где необходимо искать определитель матрицы по Вандермонду. Получаем, что
( x 2 i — 2 ) 2 x 2 i — 2 1 x 2 i — 1 ) 2 x 2 i — 1 1 ( x 2 i ) 2 x 2 i 1 , причем он считается отличным от нуля и не совпадает с точками x 2 i — 2 , x 2 i — 1 , x 2 i . Это признак того, что уравнение имеет только одно решение, тогда и выбранные коэффициенты a i ; b i ; c i могут определяться только единственным образом, тогда через точки x 2 i — 2 ; f ( x 2 i — 2 ) , x 2 i — 1 ; x 2 i — 1 , x 2 i ; f ( x 2 i ) может проходить только одна парабола.
Можно переходить к нахождению интеграла ∫ x 2 i — 2 x 2 i ( a i x 2 + b i x + c i ) d x .
f ( x 2 i — 2 ) = f ( 0 ) = a i · 0 2 + b i · 0 + c i = c i f ( x 2 i — 1 ) = f ( h ) = a i · h 2 + b i · h + c i f ( x 2 i ) = f ( 0 ) = 4 a i · h 2 + 2 b i · h + c i
Для осуществления последнего перехода необходимо использовать неравенство вида
∫ x 2 i — 2 x 2 i ( a i x 2 + b i x + c i ) d x = ∫ 0 2 h ( a i x 2 + b i x + c i ) d x = = a i x 3 3 + b i x 2 2 + c i x 0 2 h = 8 a i h 3 3 + 2 b i h 2 + 2 c i h = = h 3 8 a i h 2 + 6 b i h + 6 c i = h 3 f x 2 i — 2 + 4 f 2 2 i — 1 + f x 2 i
Значит, получаем формулу, используя метод парабол:
∫ a b f ( x ) d x ≈ ∑ i = 1 n ∫ x 2 i — 2 x 2 i a i x 2 + b i x + c i d x = = ∑ i = 1 n h 3 ( f ( x 2 i — 2 ) + 4 f ( x 2 i — 1 ) + f ( x 2 i ) ) = = h 3 f ( x 0 ) + 4 f ( x 1 ) + f ( x 2 ) + f ( x 2 ) + 4 f ( x 3 ) + f ( x 4 ) + . . . + + f ( x 2 n — 2 ) + 4 f ( x 2 n — 1 ) + f ( x 2 n ) = = h 3 f ( x 0 ) + 4 ∑ i = 1 n f ( x 2 i — 1 ) + 2 ∑ i = 1 n — 1 f ( x 2 i ) + f ( x 2 n )
Формула метода Симпсона имеет вид ∫ a b f ( x ) d x ≈ h 3 f ( x 0 ) + 4 ∑ i = 1 n f ( x 2 i — 1 ) + 2 ∑ i = 1 n — 1 f ( x 2 i ) + f ( x 2 n ) .
Формула оценки абсолютной погрешности имеет вид δ n ≤ m a x [ a ; b ] f ( 4 ) ( x ) · ( b — a ) 5 2880 n 4 .
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Примеры приближенного вычисления определенных интегралов методом парабол
Метод Симпсона предполагает приближенное вычисление определенных интегралов. Чаще всего имеются два типа задач, для которых применим данный метод:
- при приближенном вычислении определенного интеграла;
- при нахождении приближенного значения с точностью δ n .
На точность вычисления влияет значение n , чем выше n , тем точнее промежуточные значения.
Вычислить определенный интеграл ∫ 0 5 x d x x 4 + 4 при помощи метода Симпсона, разбивая отрезок интегрирования на 5 частей.
По условию известно, что a = 0 ; b = 5 ; n = 5 , f ( x ) = x x 4 + 4 .
Тогда запишем формулу Симпсона в виде
∫ a b f ( x ) d x ≈ h 3 f ( x 0 ) + 4 ∑ i = 1 n f ( x 2 i — 1 ) + 2 ∑ i = 1 n — 1 f ( x 2 i ) + f ( x 2 n )
Чтобы применить ее в полной мере, необходимо рассчитать шаг по формуле h = b — a 2 n , определить точки x i = a + i · h , i = 0 , 1 , . . . , 2 n и найти значения подынтегральной функции f ( x i ) , i = 0 , 1 , . . . , 2 n .
Промежуточные вычисления необходимо округлять до 5 знаков. Подставим значения и получим
h = b — a 2 n = 5 — 0 2 · 5 = 0 . 5
Найдем значение функции в точках
i = 0 : x i = x 0 = a + i · h = 0 + 0 · 0 . 5 = 0 ⇒ f ( x 0 ) = f ( 0 ) = 0 0 4 + 4 = 0 i = 1 : x i = x 1 = a + i · h = 0 + 1 · 0 . 5 = 0 . 5 ⇒ f ( x 1 ) = f ( 0 . 5 ) = 0 . 5 0 . 5 4 + 4 ≈ 0 . 12308 . . . i = 10 : x i = x 10 = a + i · h = 0 + 10 · 0 . 5 = 5 ⇒ f ( x 10 ) = f ( 5 ) = 5 5 4 + 4 ≈ 0 . 00795
Наглядность и удобство оформляется в таблице, приведенной ниже
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| x i | 0 | 0 . 5 | 1 | 1 . 5 | 2 | 2 . 5 |
| f x i | 0 | 0 . 12308 | 0 . 2 | 0 . 16552 | 0 . 1 | 0 . 05806 |
| i | 6 | 7 | 8 | 9 | 10 |
| x i | 3 | 3 . 5 | 4 | 4 . 5 | 5 |
| f x i | 0 . 03529 | 0 . 02272 | 0 . 01538 | 0 . 01087 | 0 . 00795 |
Необходимо подставить результаты в формулу метода парабол:
∫ 0 5 x d x x 4 + 4 ≈ h 3 f ( x 0 ) + 4 ∑ i = 1 n f ( x 2 i — 1 ) + 2 ∑ i = 1 n — 1 f ( x 2 i ) + f ( x 2 n ) = = 0 . 5 3 0 + 4 · 0 . 12308 + 0 . 16552 + 0 . 05806 + + 0 . 02272 + 0 . 01087 + 2 · 0 . 2 + 0 . 1 + + 0 . 03529 + 0 . 01538 + 0 . 00795 ≈ ≈ 0 . 37171
Для вычисления мы выбрали определенный интеграл, который можно вычислить по Ньютону-Лейбницу. Получим:
∫ 0 5 x d x x 4 + 4 = 1 2 ∫ 0 5 d ( x 2 ) x 2 2 + 4 = 1 4 a r c t g x 2 2 0 5 = 1 4 a r c t g 25 2 ≈ 0 . 37274
Ответ: Результаты совпадают до сотых.
Вычислить неопределенный интеграл ∫ 0 π sin 3 x 2 + 1 2 d x при помощи метода Симпсона с точностью до 0 , 001 .
По условию имеем, что а = 0 , b = π , f ( x ) = sin 3 x 2 + 1 2 , δ n ≤ 0 . 001 . Необходимо определить значение n . Для этого используется формула оценки абсолютной погрешности метода Симпсона вида δ n ≤ m a x [ a ; b ] f ( 4 ) ( x ) · ( b — a ) 5 2880 n 4 ≤ 0 . 001
Когда найдем значение n , то неравенство m a x [ a ; b ] f ( 4 ) ( x ) · ( b — a ) 5 2880 n 4 ≤ 0 . 001 будет выполняться. Тогда, применив метод парабол, погрешность при вычислении не превысит 0 . 001 . Последнее неравенство примет вид
n 4 ≥ m a x [ a ; b ] f ( 4 ) ( x ) · ( b — a ) 5 2 . 88
Теперь необходимо выяснить, какое наибольшее значение может принимать модуль четвертой производной.
f ‘ ( x ) = sin 3 x 2 + 1 2 ‘ = 3 2 cos 3 x 2 ⇒ f » ( x ) = 3 2 cos 3 x 2 ‘ = — 9 4 sin 3 x 2 ⇒ f ‘ ‘ ‘ ( x ) = — 9 4 sin 3 x 2 ‘ = — 27 8 cos 3 x 2 ⇒ f ( 4 ) ( x ) = — 27 8 cos 3 x 2 ‘ = 81 16 sin 3 x 2
Область определения f ( 4 ) ( x ) = 81 16 sin 3 x 2 принадлежит интервалу — 81 16 ; 81 16 , а сам отрезок интегрирования [ 0 ; π ) имеет точку экстремума, из этого следует, что m a x [ 0 ; π ] f ( 4 ) ( x ) = 81 16 .
n 4 ≥ m a x [ a ; b ] f ( 4 ) ( x ) · ( b — a ) 5 2 . 88 ⇔ n 4 ≥ 81 16 · π — 0 5 2 . 88 ⇔ ⇔ n 4 > 537 . 9252 ⇔ n > 4 . 8159
Получили, что n – натуральное число, тогда его значение может быть равным n = 5 , 6 , 7 … для начала необходимо взять значение n = 5 .
Действия производить аналогично предыдущему примеру. Необходимо вычислить шаг. Для этого
h = b — a 2 n = π — 0 2 · 5 = π 10
Найдем узлы x i = a + i · h , i = 0 , 1 , . . . , 2 n , тогда значение подынтегральной функции будет иметь вид
i = 0 : x i = x 0 = a + i · h = 0 + 0 · π 10 = 0 ⇒ f ( x 0 ) = f ( 0 ) = sin 3 · 0 2 + 1 2 = 0 . 5 i = 1 : x i = x 1 = a + i · h = 0 + 1 · π 10 = π 10 ⇒ f ( x 1 ) = f ( π 10 ) = sin 3 · π 10 2 + 1 2 ≈ 0 . 953990 . . . i = 10 : x i = x 10 = a + i · h = 0 + 10 · π 10 = π ⇒ f ( x 10 ) = f ( π ) = sin 3 · π 2 + 1 2 ≈ — 0 . 5
Для объединения результатов запишем данные в таблицу.
| i | 0 | 1 | 2 | 3 | 4 |
| x i | 0 | π 10 | π 5 | 3 π 10 | 2 π 5 |
| f ( x i ) | 0 . 5 | 0 . 953990 | 1 . 309017 | 1 . 487688 | 1 . 451056 |
| i | 5 | 6 | 7 | 8 | 9 | 10 |
| x i | π 2 | 3 π 5 | 7 π 10 | 4 π 5 | 9 π 10 | π |
| f ( x i ) | 1 . 207107 | 0 . 809017 | 0 . 343566 | — 0 . 087785 | — 0 . 391007 | — 0 . 5 |
Осталось подставить значения в формулу решения методом парабол и получим
∫ 0 π sin 3 x 2 + 1 2 ≈ h 3 f ( x 0 ) + 4 ∑ i = 1 n f ( x 2 i — 1 ) + 2 ∑ i = 1 n — 1 f ( x 2 i ) + f ( x 2 n ) = = π 30 · 0 , 5 + 4 · 0 . 953990 + 1 . 487688 + 1 . 207107 + + 0 . 343566 — 0 . 391007 + 2 · 1 . 309017 + 1 . 451056 + + 0 . 809017 — 0 . 87785 — 0 . 5 = = 2 . 237650
Метод Симпсона позволяет нам получать приближенное значение определенного интеграла ∫ 0 π sin 3 x 2 + 1 2 d x ≈ 2 . 237 с точностью до 0 , 001 .
При вычислении формулой Ньютона-Лейбница получим в результате
∫ 0 π sin 3 x 2 + 1 2 d x = — 2 3 cos 3 x 2 + 1 2 x 0 π = = — 3 2 cos 3 π 2 + π 2 — — 2 3 cos 0 + 1 2 · 0 = π 2 + 2 3 ≈ 2 . 237463
Ответ: ∫ 0 π sin 3 x 2 + 1 2 d x ≈ 2 . 237
Видео:Численное интегрирование. Метод СимпсонаСкачать

Замечание
В большинстве случаях нахождение m a x [ a ; b ] f ( 4 ) ( x ) проблематично. Поэтому применяется альтернатива – метод парабол. Его принцип подробно разъясняется в разделе метода трапеций. Метод парабол считается предпочтительным способом для разрешения интеграла. Вычислительная погрешность влияет на результат n . Чем меньше его значение, тем точнее приближенное искомое число.
Видео:16. Формула Симпсона ( практический курс по сопромату )Скачать

Метод Симпсона
Вы будете перенаправлены на Автор24
В случае с методом Симпсона для вычисления интегралов в отличие от метода прямоугольников и метода трапеций, функция кривой $y=f(x)$ на элементарных отрезках $left[x_;x_iright]$ заменяется не отрезками прямых, а дугами парабол, в результате получается более точная формула для приближённого вычисления интеграла $int_a^b f(x)dx$.
Видео:Численное интегрирование: Методы Левых Правых прямоугольников, Трапеций, Симпсона c++Скачать

Вывод формулы Симпсона
Для начала рассмотрим, как найти площадь криволинейной трапеции, ограниченной сверху функцией $y=ax^2+bx+c$, по бокам прямыми, параллельными оси ординат $x=-h$, $x=h$, а снизу отрезком, параллельным оси абсцисс.
Рисунок 1. Вычисление площади криволинейной трапеции
Парабола проходит через три точки $M_1, M_2$ и $M_3$ c координатами соответственно $(-h; y_0), (0; y_1)$ и $(h;y_2)$. При этом функция $y$ в точке $(-h; y_0)$ будет равна $y_0=ah^2-bh+c$, в точке $(0; y_1)$ она равна $y_1=c$, так как $x=0$, а в точке $(h;y_2)$ она имеет значение $y_2= ah^2+bh+c$.
Соответственно, площадь $S$ равна:
Из формул, описывающих значения функций в рассматриваемых точках, получаем, что $c=y_1, a =frac(y_0-2y_1+y_2)$. Подставим эти значения в выражение $(1)$, получим:
$S=frach^3 cdot frac(y_0-2y_1+y_2)+2hy_1= frac(y_0-2y_1+y_2) + 2hy_1 = frac cdot (y_0 + 4y_1+y_2)left(2right)$
Полученная формула является формулой для вычисления площади криволинейной трапеции. Перейдём от неё к формуле парабол для приближённого вычисления определённого интеграла.
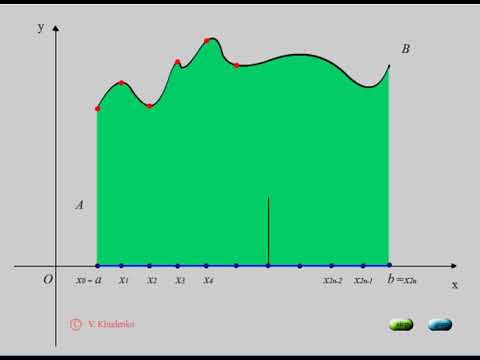
Сначала разобьём отрезок $left[a;bright]$ на $2n$ равных отрезков длиной $h=frac$, для этого отложим точки $x_i=x_0+ih, (i=0. 2n)$, причём $x_0=a$, a $x_=b$. Получим $2n$ элементарных трапеций (рис. 2). В каждой из этих точек с абсциссой $x_i$ вычисляем значение функции $y$.
Готовые работы на аналогичную тему
Рисунок 2. Вычисление площади фигуры, ограниченной линиями, по методу Симпсона
Теперь перейдём от элементарных трапеций к формуле Cимпсона для вычисления интеграла. Для этого каждую пару элементарных криволинейных трапеций, основания у которых равны $h$, заменяем на одну трапецию с основанием $2h$. Рассматриваем кривую $y=f(x)$ на отрезке $left[x_0;x_2right]$, она проходит через 3 точки с координатами $(x_0;y_0), (x_1;y_1), (x_2;y_2)$. Подставим их в формулу $(2)$:
Аналогично находим все остальные площади:
Теперь складываем полученные равенства и получаем:
Полученная формула носит название метода парабол или иначе формула Симпсона.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Оценка погрешности при использовании метода парабол
Погрешность для метода парабол вычисляется по формуле:
Формула Симпсона даёт точное значение для всех функций, в которых максимальная степень при $x$ меньше или равна $3$, так как четвёртая производная в этом случае равна нулю.
Нахождение определённого интеграла не всегда удобно из-за трудности вычисления $M_4$, поэтому при возникновении сложностей пользуются методом трапеций.
Вычислите интеграл $int^2_0 x^3dx$ при этом разбив отрезок интегрирования на 4 элементарных.
Решение:
Для начала проведём подготовительные вычисления для функции $f(x)=x^3$:
$a=0=x_0, b=2=x_4$, следовательно, длина элементарного отрезка составит:
Определяем координаты границ элементарных отрезков:
Теперь воспользуемся формулой парабол и вычислим интеграл:
Так как четвёртая производная функции $y(x)=x^3$ равна нулю, погрешность метода в данном случае также будет нулевой.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 25 02 2021
Видео:Интеграл Мора 3 Формулы Симпсона и трапецийСкачать

Правило Симпсона: формула, доказательство, примеры, упражнения
Правило Симпсона: формула, доказательство, примеры, упражнения — Наука
Видео:Решение системы уравнений методом ГауссаСкачать

Содержание:
В правило симпсонов является методом приближенного вычисления определенных интегралов. Он основан на делении интервала интегрирования на четное количество равноотстоящих подинтервалов.
Крайние значения двух последовательных подинтервалов определяют три точки, по которым подходит парабола, уравнение которой является полиномом второй степени.
Затем площадь под кривой функции в двух последовательных интервалах аппроксимируется площадью интерполяционного полинома. Добавляя вклад в площадь под параболой всех последовательных подинтервалов, мы получаем приблизительное значение интеграла.
С другой стороны, поскольку интеграл от параболы может быть вычислен алгебраически точно, то можно найти аналитическую формулу для приближенного значения определенного интеграла. Он известен как Формула Симпсона.
Погрешность полученного таким образом приближенного результата уменьшается по мере увеличения числа подразделений n (где n — четное число).
Ниже будет приведено выражение, позволяющее оценить верхнюю границу погрешности приближения интеграла I, когда выполнено разбиение n регулярных подинтервалов общего интервала [a, b].
Видео:Формула СимпсонаСкачать

Формула
Интервал интегрирования [a, b] разделен на n подинтервалов, где n — четное целое число. Ширина каждого подразделения будет:
Таким образом, на отрезке [a, b] выполняется разбиение:
Где X0 = a, X1 = X0 + h, X2 = X0 + 2h,…, Xn-1 = X0 + (n-1) h, Xn = X0 + nh = b.
Формула, позволяющая аппроксимировать определенный интеграл I от непрерывной и предпочтительно гладкой функции на интервале [a, b], имеет следующий вид:
Видео:3. Численные методы расчета определенного интеграла: прямоугольников, трапеции, парабол (Симпсона)Скачать
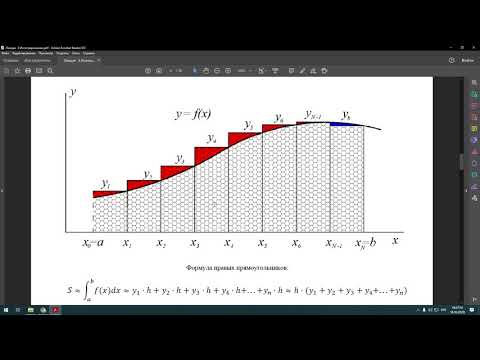
Демонстрация
Чтобы получить формулу Симпсона, в каждом подынтервале [Xi, Xi + 2] функция f (X) аппроксимируется многочленом второй степени p (X) (параболой), проходящим через три точки: [Xi, f ( Xi)]; [Xi + 1, f (Xi + 1)] и [Xi + 2, f (Xi + 2)].
Затем мы вычисляем интеграл от многочлена p (x) в [Xi, Xi + 2], который аппроксимирует интеграл от функции f (X) в этом интервале.
Видео:Метод Симпсона - ВизуализацияСкачать

Коэффициенты интерполяционного полинома
Уравнение параболы p (X) имеет общий вид: p (X) = A X 2 + B X + C. Поскольку парабола проходит через точки Q, указанные красным (см. Рисунок), то коэффициенты A, B, C определяются из следующей системы уравнений:
А (-h) 2 — B h + C = f (Xi)
А (ч) 2 + B h + C = f (Xi + 2)
Видно, что коэффициент C определен. Для определения коэффициента A складываем первое и третье уравнения, получая:
2 А ч 2 + 2 С = f (Xi) + f (Xi + 2).
Затем значение C подставляется и A очищается, оставляя:
A = [f (Xi) — 2 f (Xi + 1) + f (Xi + 2)] / (2 h 2 )
Чтобы определить коэффициент B, третье уравнение вычитается из первого и решается B, получая:
B = [f (Xi + 2) — f (Xi)] = 2 ч.
Таким образом, многочлен второй степени p (X), который проходит через точки Qi, Qi + 1 и Qi + 2, имеет коэффициенты:
A = [f (Xi) — 2 f (Xi + 1) + f (Xi + 2)] / (2 h 2 )
B = [f (Xi + 2) — f (Xi)] = 2 ч.
Видео:Задача 4.2.3 Интеграл Мора. Метод СимпсонаСкачать

Вычисление приближенного интеграла в [Xi, Xi + 2]
Видео:Метод прямоугольников для нахождения определенного интегралаСкачать

Приближенное вычисление интеграла в [a, b]
Как уже было сказано, на всем интервале интегрирования [a, b] делается разбиение с шагом h = Xi + 1 — Xi = (b — a ) / n, где n — четное число.
Видео:Универсальная формула СимпсонаСкачать

Ошибка приближения
Обратите внимание, что ошибка уменьшается с четвертой степенью количества делений в интервале. Например, если вы перейдете от n подразделений к 2n, то ошибка уменьшится в 1/16 раза.
Верхняя граница ошибки, полученная с помощью приближения Симпсона, может быть получена по той же формуле, заменив четвертой производной максимальное абсолютное значение четвертой производной в интервале [a, b].
Видео:Решение системы уравнений методом Крамера 2x2Скачать

Примеры работы
Видео:Численные методы решения интегралов в MS ExcelСкачать

— Пример 1
Рассмотрим функцию f (X) = 1 / (1 + X 2 ).
Найти определенный интеграл функции f (X) на отрезке [-1, 1], используя метод Симпсона с двумя подразделениями (n = 2).
Видео:3.2 Численное интегрирование (лекция)Скачать
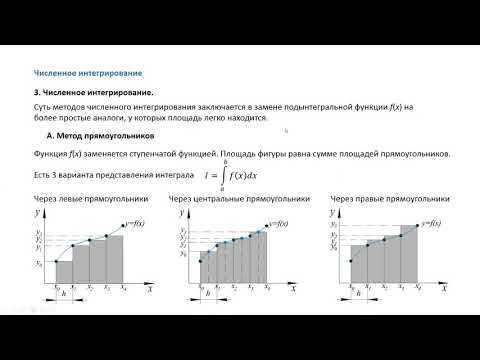
Решение
Мы берем n = 2. Пределы интегрирования равны a = -1 и b = -2, поэтому разбиение выглядит так:
Х0 = -1; X1 = 0 и X2 = +1.
Следовательно, формула Симпсона принимает следующий вид:
При n = 2 → xo = -1, x1 = 0; x2 = 1, поэтому:
Видео:Численное интегрированиеСкачать

— Пример 2
Рассмотрим функцию f (X) = 1 / (1 + X 2 ).
Найдите определенный интеграл функции f (X) на интервале [-1, 1], используя формулу Симпсона с четырьмя подразделениями (n = 4).
Решение
Возьмем n = 4. Пределы интегрирования a = -1 и b = -2, поэтому разбиение выглядит так:
Х0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 и X4 = +1.
Формула Симпсона сформулирована так:
Интеграл ≃ [(b -a) / (3 n)] [f (X0) + 4 I + 2 P + f (Xn)]
Для случая, когда он применяется, он выглядит следующим образом:
Интеграл ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1,5666
— Пример 3
Определите точный интеграл из предыдущих примеров и сравните точный результат с результатами, полученными с использованием формулы Симпсона в примерах 1a и 1b.
Решение
Неопределенный интеграл функции f (X) = 1 / (1 + X 2 ) — функцияарктан (X).
При оценке в пределах интеграции остается:
Интеграл = arctan (1) — arctan (-1) = π / 4 — (-π / 4) = π / 2 = 1,5708
Если сравнить результат точного решения с результатом, полученным методом Симпсона при n = 2 и n = 4, мы имеем:
Для n = 2 разница между точным и приближенным решением составляет π / 2 — 5/3 = -0,0959, то есть разница в процентах составляет -0,06%.
А для приближения Симпсона с n = 4 разница между точным и приближенным решением составляет π / 2 — 47/30 = 0,0041, то есть разница в процентах 0,003%.
Предлагаемое упражнение
Метод Симпсона подходит для применения в языках программирования и в компьютерных приложениях для математических вычислений. Предлагаем читателю, основываясь на формулах, приведенных в этой статье, написать собственный код в своей любимой программе.
На следующем рисунке показано упражнение, в котором формула Симпсона была реализована в Smath studio, бесплатное программное обеспечение для операционных систем Windows Y Android.