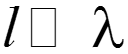
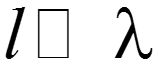
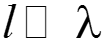
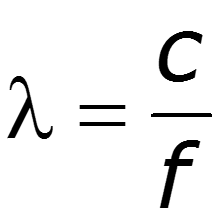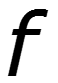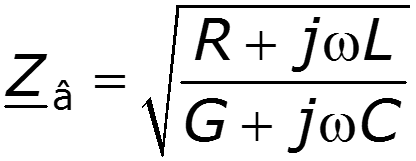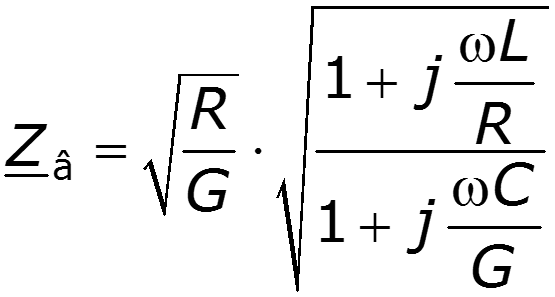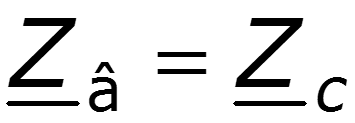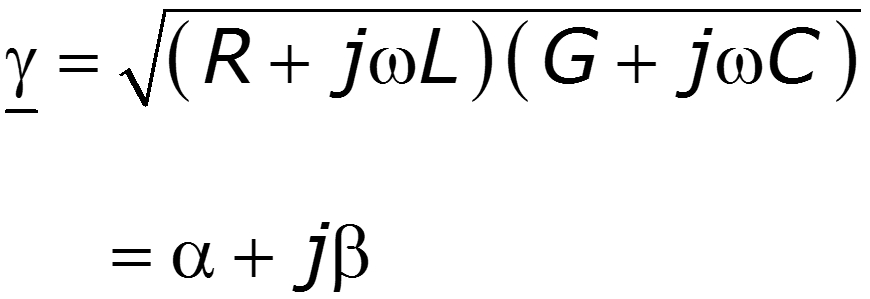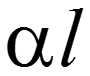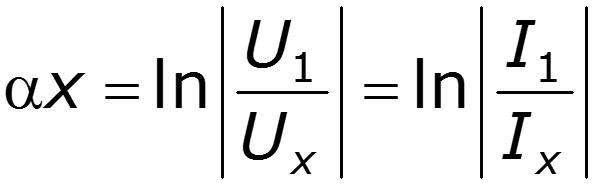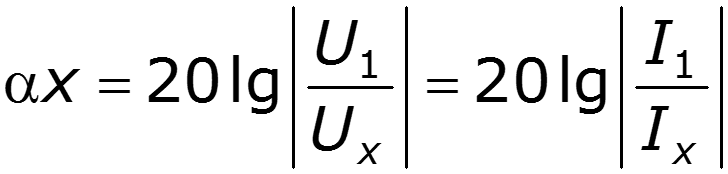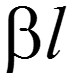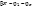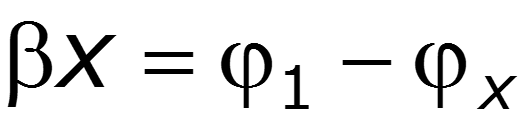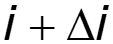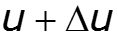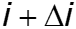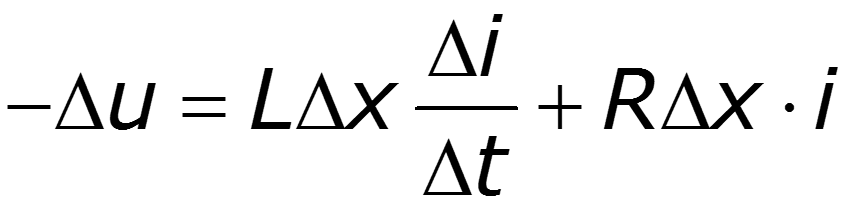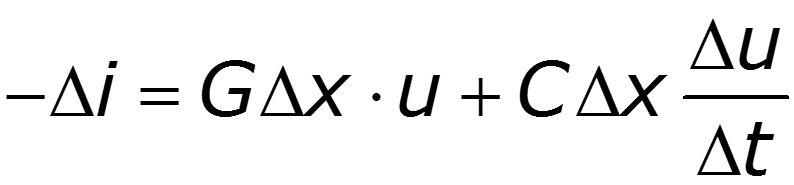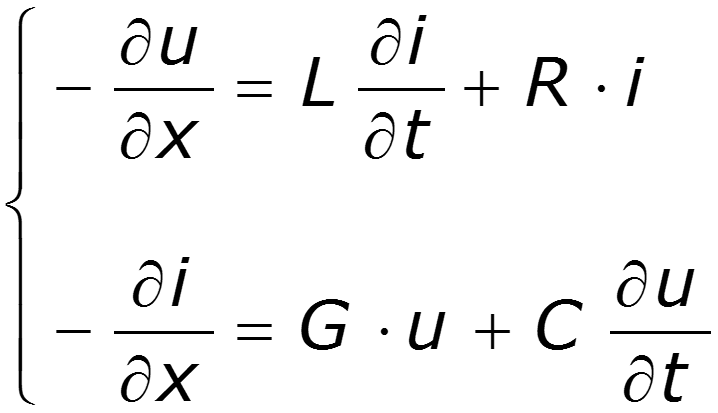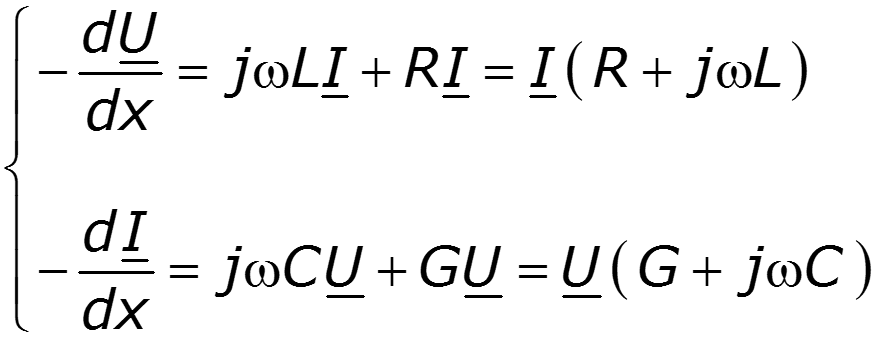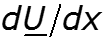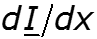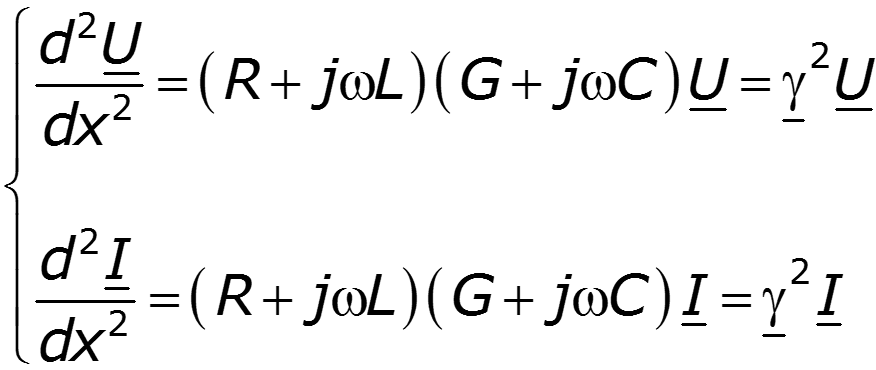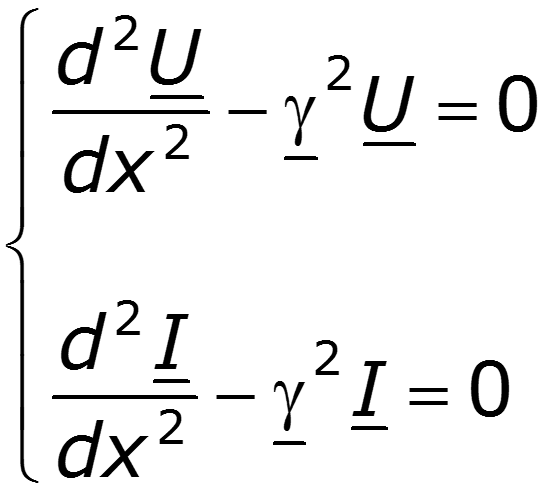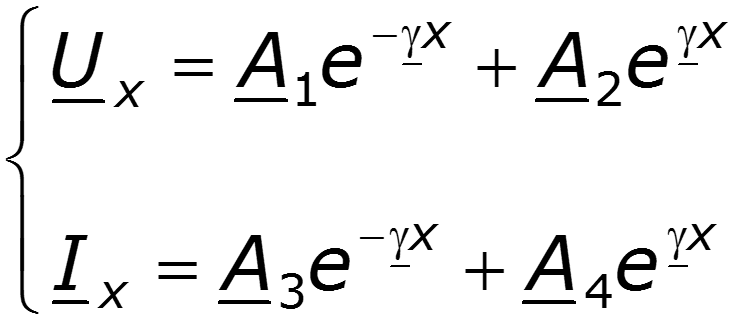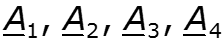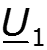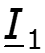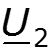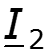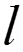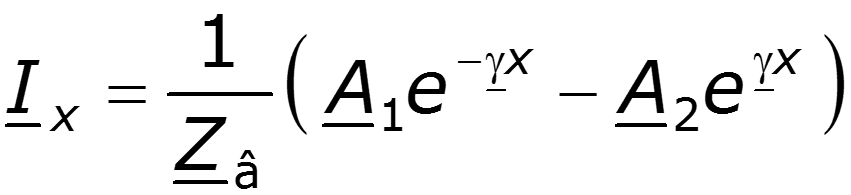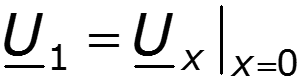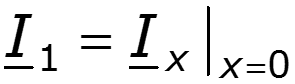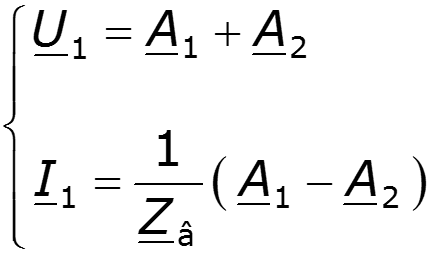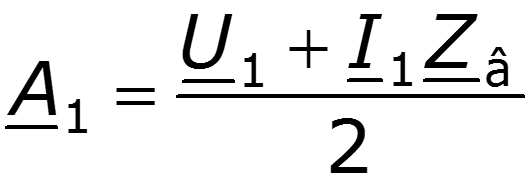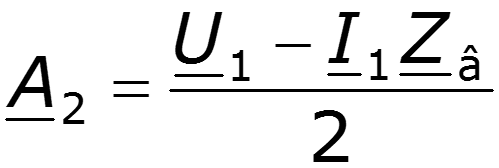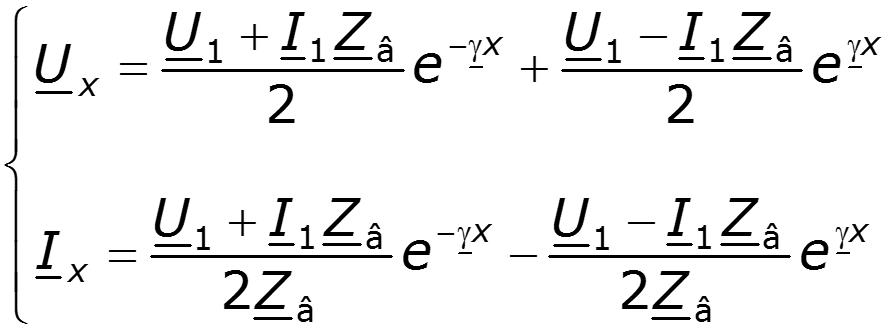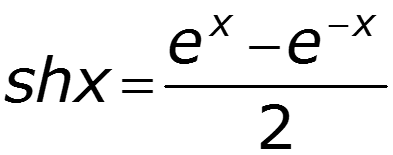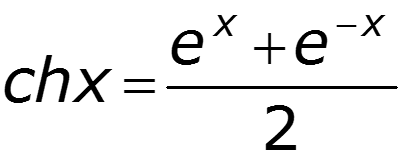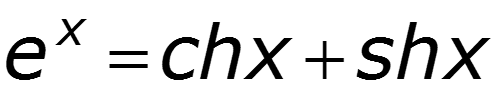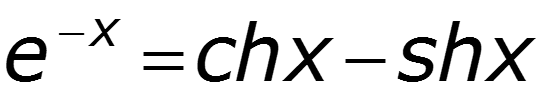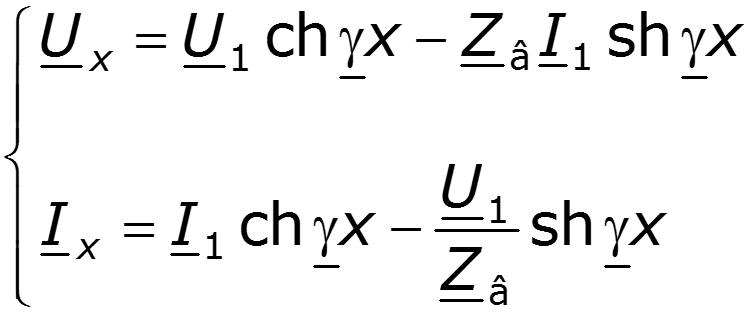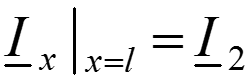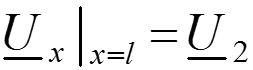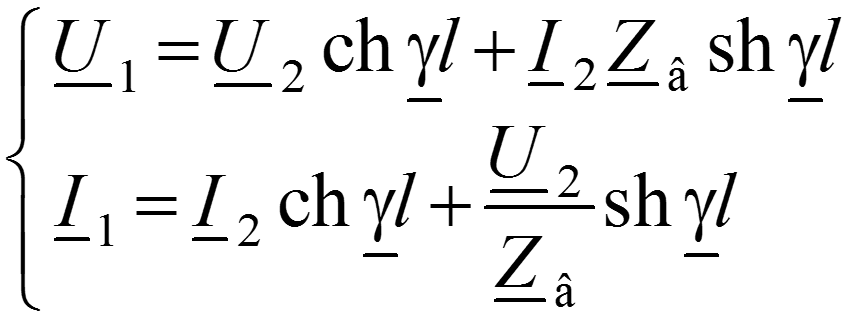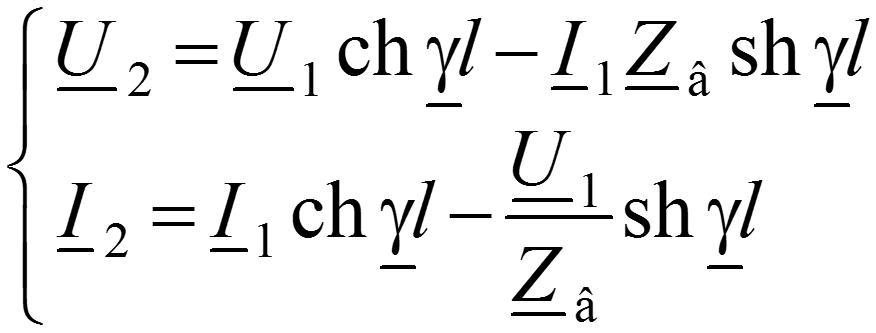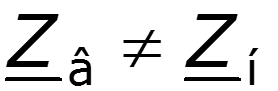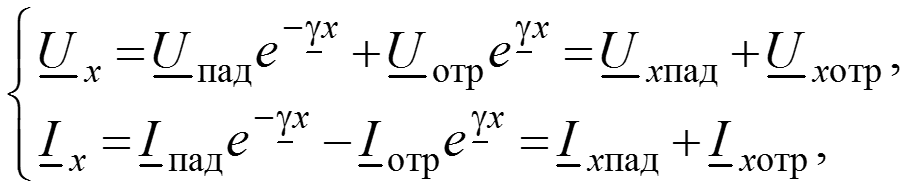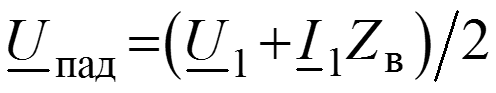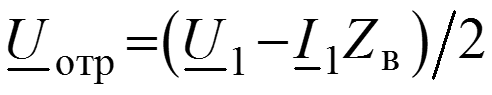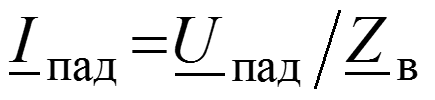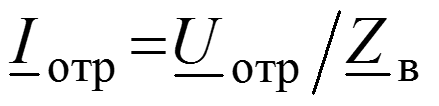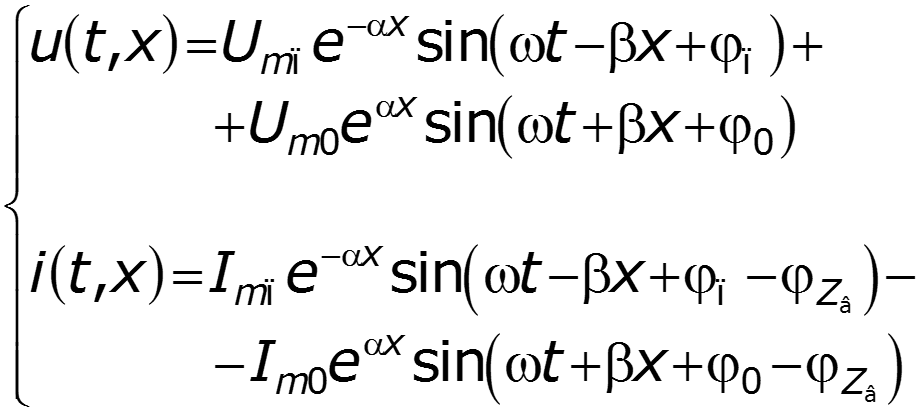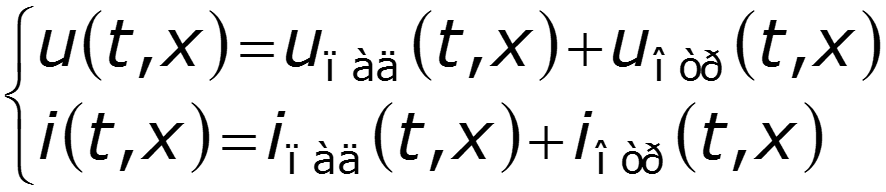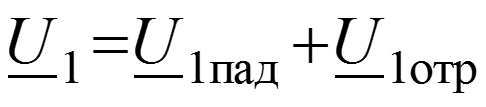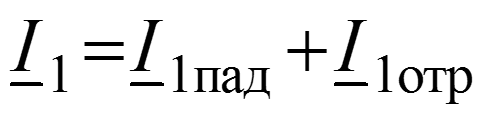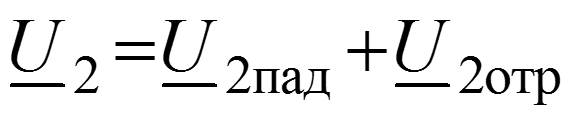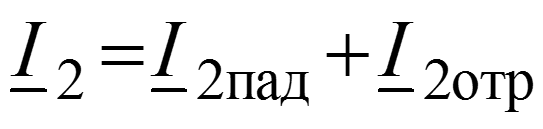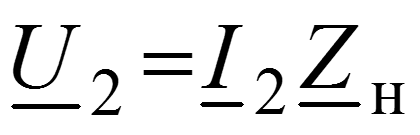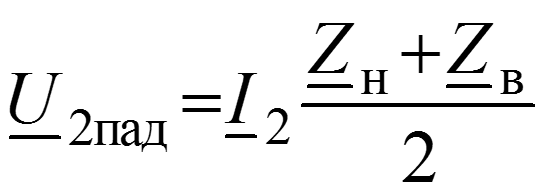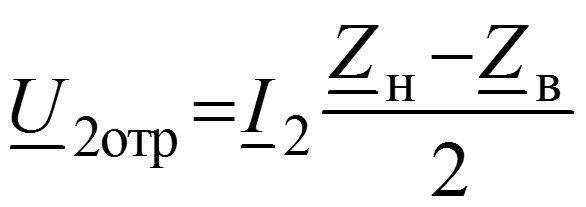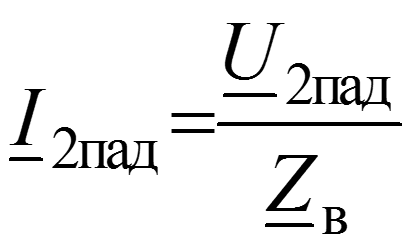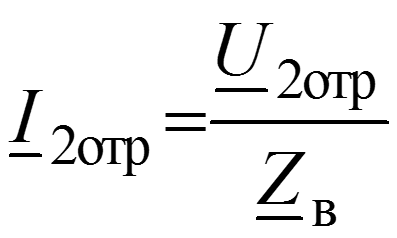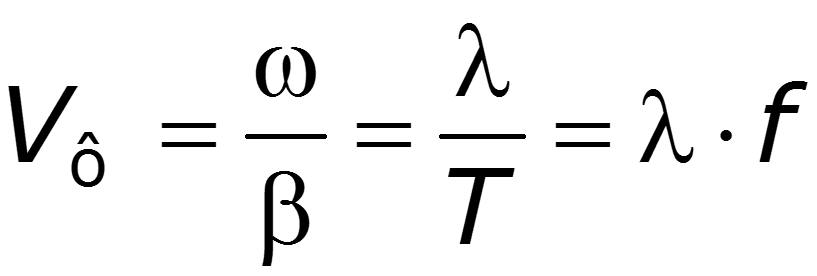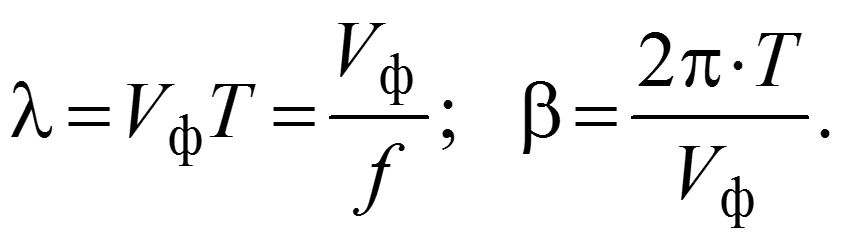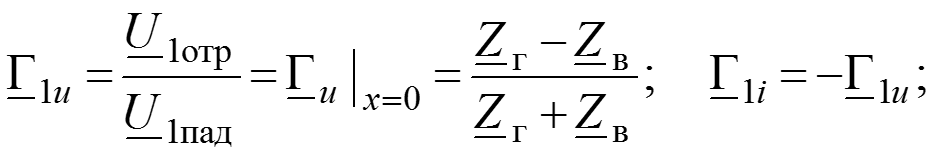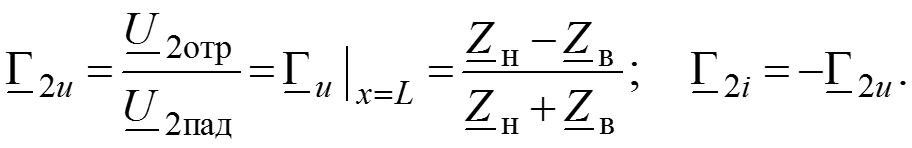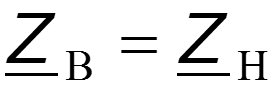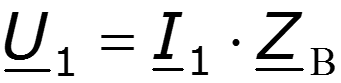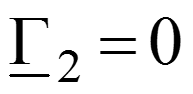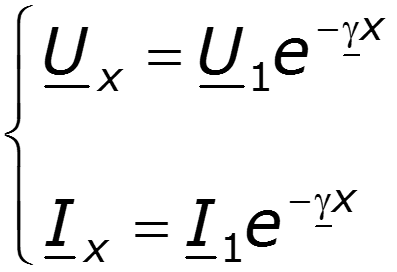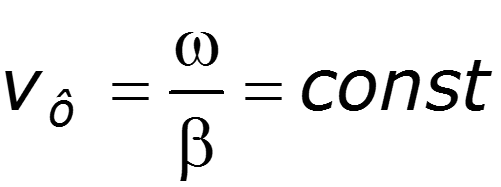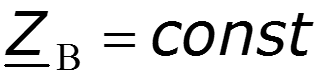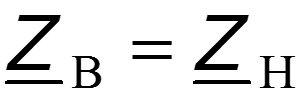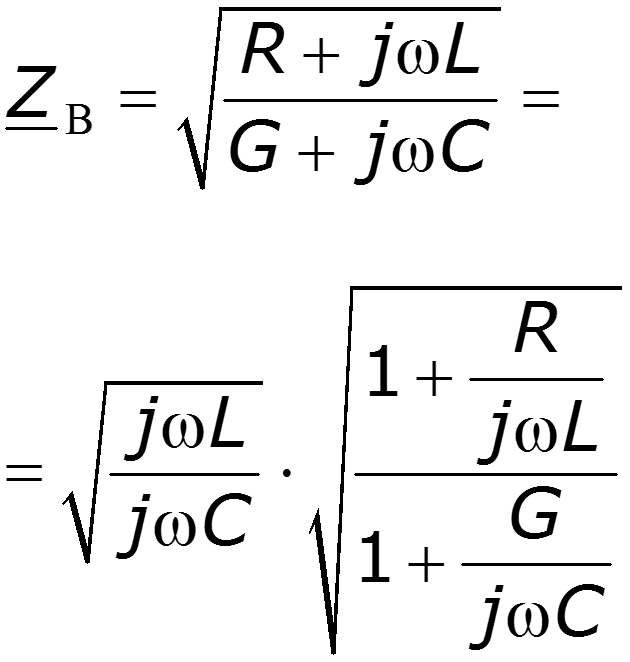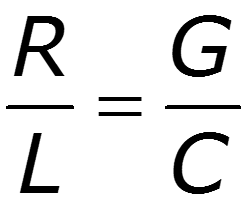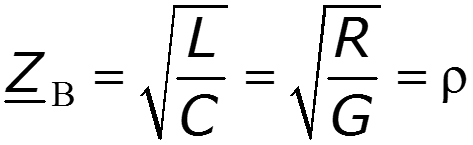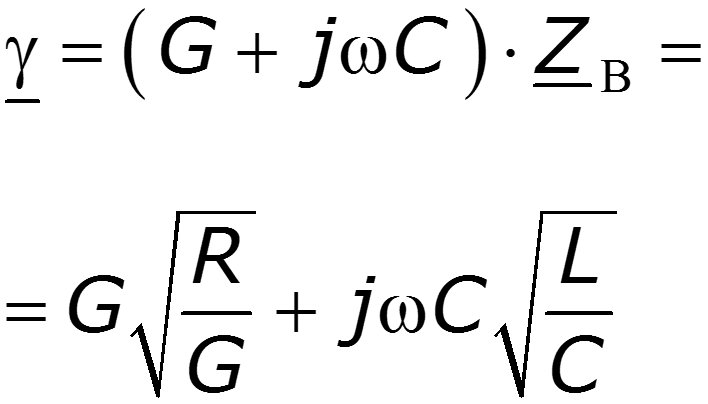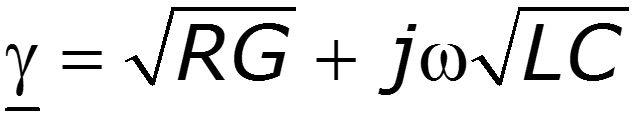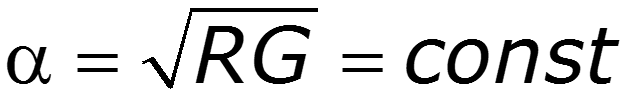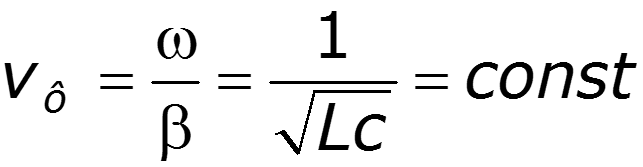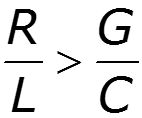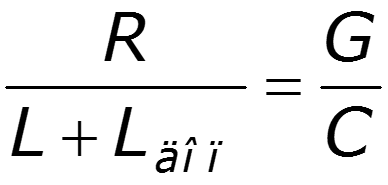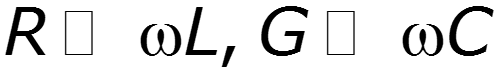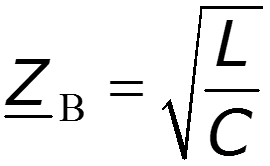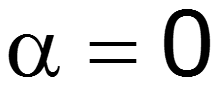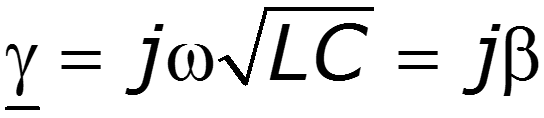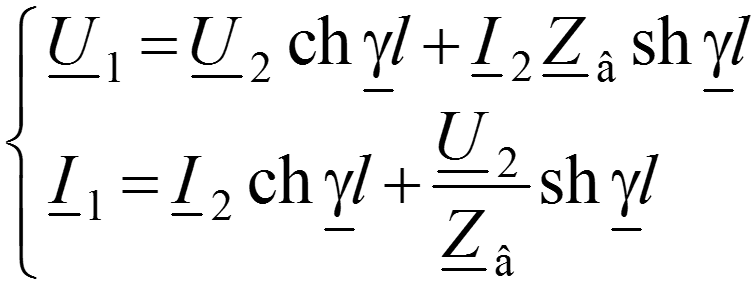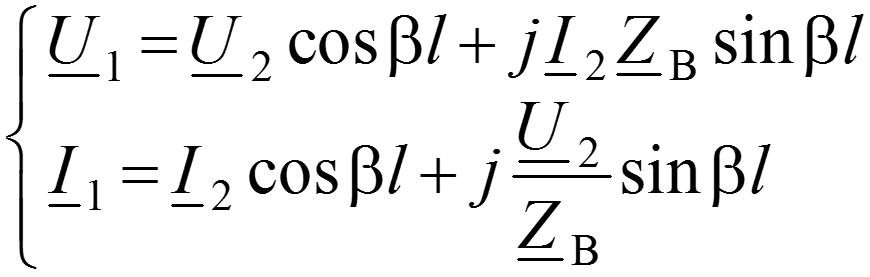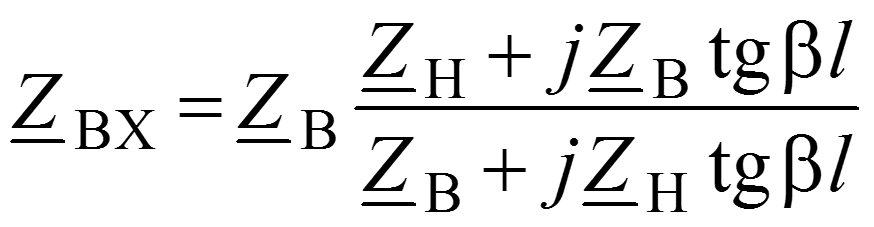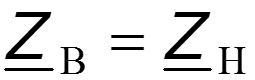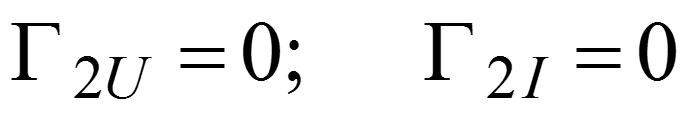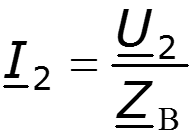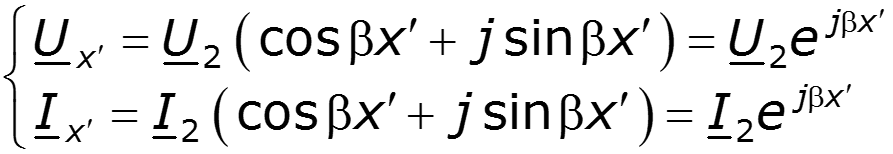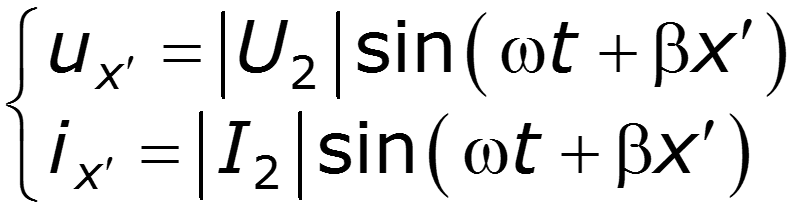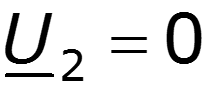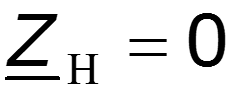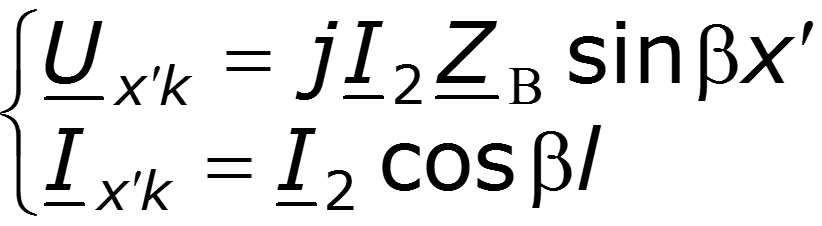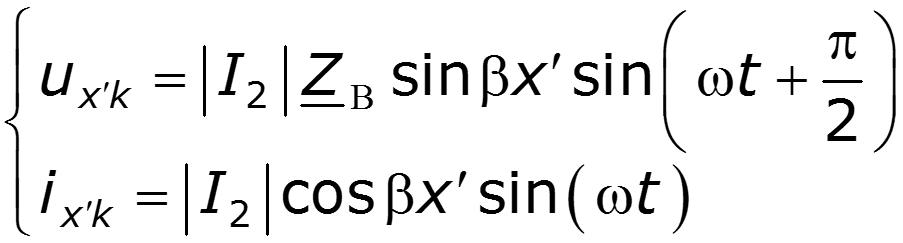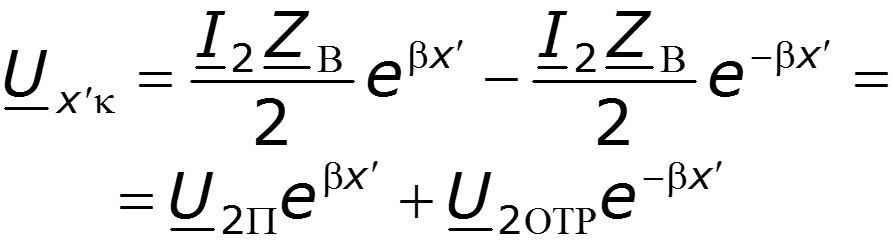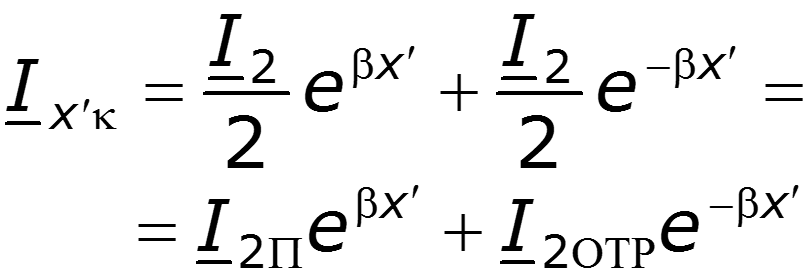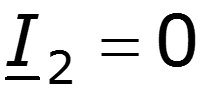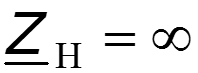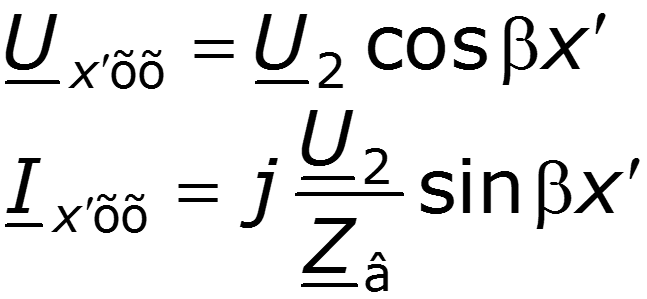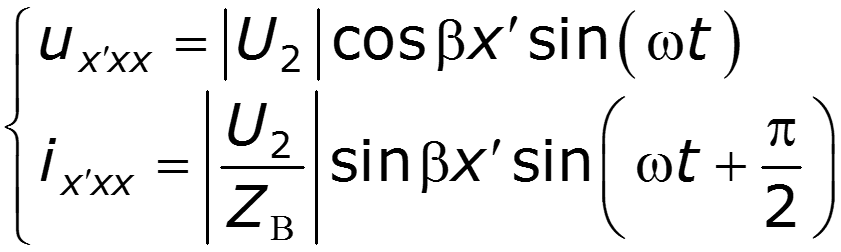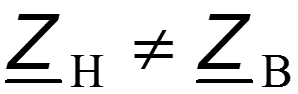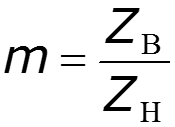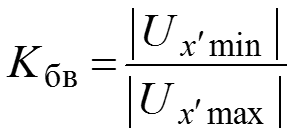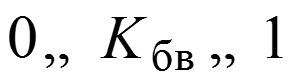5. Решение уравнений состояния. Выполняется численным методом (например, Рунге-Кутта [9]). Если характеристики рис. 11.53 линеаризовать (подобно тому, как это было сделано в примере 11.13) и оценить реальную длительность переходного процесса, то можно выбрать шаг по времени Dt. При наличии колебательного процесса в линеаризованной цепи должно быть 
и 
, где 
и 
– постоянная времени и период свободных колебаний. Если же в этой цепи протекает апериодический процесс, то следует принять 
. При этом будет обеспечена приемлемая для учебных целей точность расчета. Вычисления начинаются с найденных в п.1 значений q(0), 
и продолжаются до тех пор, пока не будут достигнуты (с заданной точностью) значения q(¥), 
из п.2.
12. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
12.1. Общие положения
12.1.1. основные понятия и определения
Параметры реальной электрической цепи практически всегда распределены по длине ее участков. Но при решении большинства практических задач это обстоятельство не оказывает существенного влияния на результаты анализа. В этих случаях можно считать, что сопротивления, индуктивности, емкости сосредоточены на определенных участках цепи и соответствующим образом отражаются в схеме замещения. Такое допущение с успехом использовалось во всех предыдущих разделах курса, где рассматривались цепи с сосредоточенными параметрами.
Однако существуют и задачи, условия которых просто не позволяют пренебречь распределением параметров. Устройство можно рассматривать как электрическую цепь, если оно имеет достаточно большую протяженность только в определенном направлении. В этом случае можно говорить о распределении параметров именно в этом направлении. Необходимость учета распределения параметров цепи вдоль некоторого направления возникает в тех случаях, когда промежуток времени, за который электромагнитная волна распространяется вдоль цепи в этом направлении, соизмерим с интервалом времени, за который токи и напряжения в цепи могут измениться на заметную величину. Разумеется, токи и напряжения при этом оказываются функциями двух независимых переменных: времени t и расстояния x. Поэтому уравнения, описывающие состояние цепи с распределенными параметрами, – это уравнения в частных производных.
Примерами таких цепей служат, в первую очередь, протяженные линии электропередачи, линии связи, высокочастотные линии радиотехнических и телевизионных устройств. Впрочем, и обмотки трансформаторов, и обмотки электрических машин, работающих в импульсном режиме, также должны рассматриваться как цепи с распределенными параметрами.
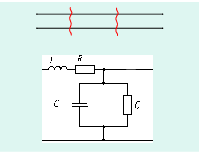
Выберем в качестве объекта исследования двухпроводную линию. Нам придется считать, что каждый сколь угодно малый элемент длины линии обладает параметрами, отражающими в схеме замещения известные явления. Как обычно, сопротивление будет учитывать тепловые потери в проводах, индуктивность – явление самоиндукции при изменении магнитного потока, емкость – токи смещения между проводами, а проводимость – токи утечки по изоляции. Если эти параметры равномерно распределены по длине, то такую линию называют однородной. Выведем уравнения, описывающие состояние однородной двухпроводной линии, считая ее параметры на единицу длины 
, 
, 
, 
известными и независящими от частоты. Эти параметры называют первичными. Заметим, что при необходимости подобные уравнения нетрудно применить и к исследованию трехфазной линии, работающей в симметричном режиме, используя ее схему замещения на одну фазу.
12.1.2. Уравнения однородной двухпроводной линии
в частных производных
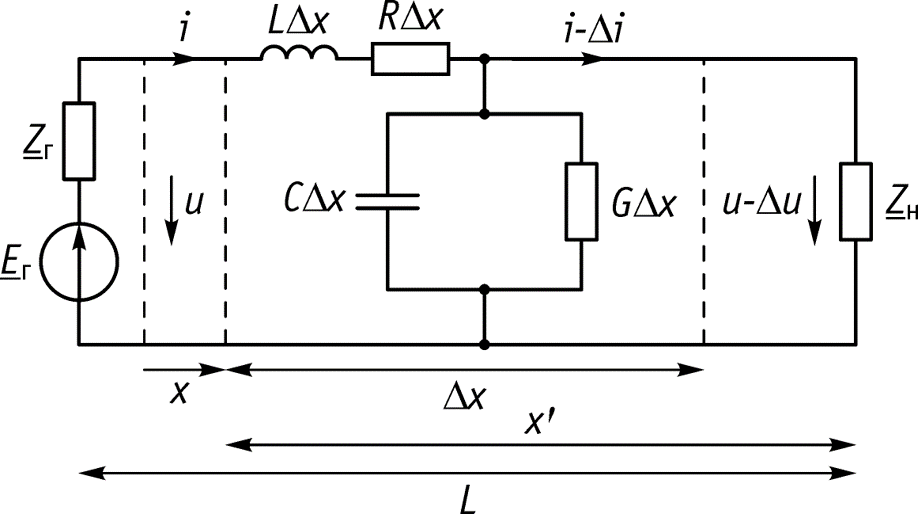
Выделим на расстоянии х от начала линии элемент линии длиной dx, на входе которого существуют напряжение u и ток i (рис. 12.1,а). На выходе эти величины получают приращения 
и 
. Первое связано с падениями напряжения на сопротивлении 
и индуктивности 
, по которым в схеме замещения (рис. 12.1,б) протекает ток i. Второе – с утечками по проводимости 
и током смещения через емкость 
, которые находятся под напряжением 
. По законам Кирхгофа имеем:
Приводя подобные, пренебрегая величинами второго порядка малости, после деления на dx, получим уравнения однородной двухпроводной линии в частных производных:
(12.1)
Решение этой системы уравнений при заданных начальных и граничных условиях позволяет определить искомые зависимости i(x,t) и u(x,t). Уравнения справедливы для описания как установившихся, так и переходных режимов.
12.2. установившийся синусоидальный режим
работы однородной двухпроводной линии
12.2.1. Уравнения линии в установившемся
Для решения уравнений линии в частных производных в установившемся синусоидальном режиме используем комплексный метод. При переходе от синусоидальных функций времени к их комплексным изображениям окажется, что
Поэтому уравнения (12.1) в комплексной форме записи примут вид:
Обозначив здесь 
– комплексное продольное сопротивление, а 
– комплексную поперечную проводимость единицы длины линии, получим
(12.2)
Подстановка I из первого уравнения системы (12.2) во второе, приводит к линейному дифференциальному уравнению второго порядка
с комплексно сопряженными корнями характеристического уравнения ±g. Решение такого уравнения можно записать в виде суммы экспонент:
. (12.3)
Здесь 
– (12.4)
коэффициент распространения линии, 
, 
, 
и 
– постоянные интегрирования.
Подстановка выражения (12.3) в первое уравнение системы (12.2) позволяет найти комплекс тока
, (12.5)
где величина 
(12.6)
имеет размерность сопротивления.
Для того, чтобы выяснить физический смысл слагаемых, входящих в формулы (12.3), (12.5), и их отношения (12.6), перейдем от комплексных величин к функциям времени.
12.2.2. Бегущие волны
Запишем в показательной форме комплексы
и 
Тогда мгновенные значения величин, соответствующих комплексным слагаемым в выражении (12.3), примут вид:
При фиксированном значении координаты 
каждая из этих величин изменяется во времени по синусоидальному закону с периодом 
. А в любой фиксированный момент времени 
распределение напряжения вдоль линии происходит по закону затухающей синусоиды с 
(длина волны – расстояние между двумя ближайшими точками линии, в которых фазы синусоид тока или напряжения волны отличаются на 
). При этом затухание 
происходит от начала линии к концу, то есть в сторону увеличения координаты х, а 
затухает от конца к началу (в сторону уменьшения х). На рис. 12.2 показано распределение составляющей вдоль х в моменты времени 
и 
. Подобным же образом ведет себя и зависимость
Если же зафиксировать фазу синусоиды 
и продифференцировать это выражение по времени, то получится
, отсюда
. (12.7)
Это означает, что мы имеем дело с электромагнитной волной, которая движется в сторону увеличения х с фазовой скоростью 
. По мере перемещения амплитуды напряжения и тока затухают. Назовем эту волну прямой. На рис. 12.2 видно, что за время 
нули на графике функции перемещаются на расстояние 
.
Очевидно, с помощью аналогичных рассуждений можно показать, что вторая пара составляющих напряжения и тока
характеризует обратную волну, которая движется в сторону уменьшения х с той же самой скоростью. Причем амплитуды напряжения и тока также затухают по мере продвижения волны.
Поэтому комплекс 
можно назвать волновым сопротивлением линии. Оно равно отношению комплексов напряжения и тока в любой точке линии, когда в ней существует только одна волна – неважно какая, прямая или обратная.
В свою очередь коэффициент распространения характеризует изменение тока и напряжения волны по мере ее продвижения. Действительно, из формул (12.3–12.6) следует:
.
Выбор отрезка Dх, равного единице длины, позволяет дать следующие определения.
Коэффициент затухания 
показывает, насколько отличаются логарифмы действующих значений напряжений или токов одной волны в точках, отстоящих друг от друга на единицу длины. Единица измерения – непер на метр [Нп/м] или на километр.
Коэффициент фазы 
показывает, насколько отличаются фазы напряжений или токов одной волны в тех же самых точках. Единица измерения – радиан на метр [рад/м] или на километр.
и 
называют вторичными параметрами линии, они, также как и первичные, полностью характеризуют линию.
Таким образом, установившийся синусоидальный режим работы линии можно рассматривать как результат наложения двух затухающих бегущих в противоположных направлениях с одинаковой скоростью волн. Если х отсчитывается от начала линии (рис. 12.1,а), то возникновение обратной волны можно рассматривать как результат отражения прямой волны от нагрузки и называть волны падающей и отраженной.
Пометим индексом 2 значения величин в конце линии (x = l), где включена нагрузка с комплексным сопротивлением 
. Тогда
Отсюда нетрудно найти коэффициент отражения:
. (12.8)
В частности в режимах холостого хода 
и короткого замыкания 
происходит полное отражение волны (N = ±1 соответственно). При 
отражения не происходит (N = 0), в линии существует только одна волна и вся принесенная ею энергия поглощается нагрузкой. Такой режим называется режимом согласованной нагрузки.
При согласованной нагрузке мощность в начале линии равна
и коэффициент полезного действия
.
Известны волновое сопротивление и коэффициент распространения линии электропередачи, работающей на промышленной частоте f = 50 Гц: 
, 
1/км.
Определить первичные параметры линии: , , , .
Воспользовавшись формулами (12.4) и (12.6), найдем:
Отсюда 
и 
Затем вычисляем угловую частоту 
и, наконец,
12.2.3. Уравнения линии в гиперболических функциях
Определим постоянные интегрирования в уравнениях (12.3) и (12.5) из граничных условий, считая, что в начале линии (х = 0 на рис. 12.3,а) и напряжение 
, и ток 
известны. Тогда эти уравнения переписываются в виде: 
откуда легко найти
После подстановки постоянных в уравнения (12.3), (12.5) и приведения подобных заметим, что
В результате получим уравнения линии в гиперболических функциях:
(12.9)
Подстановка x = l дает:
Если разрешить эти уравнения относительно 
, , то они примут вид:
Последние две системы уравнений совпадают по форме с уравнениями четырехполюсника в гиперболических функциях, характеристическое сопротивление и постоянная передачи которого очень просто выражаются через вторичные параметры линии:
Соответственно коэффициенты затухания и фазы такого эквивалентного линии четырехполюсника равны:
Все эти параметры определяются в режиме согласованной нагрузки (см. раздел 9.7 [6]).
Очевидно, при отсчете расстояния y от конца линии (рис.12.3,б) уравнения линии в гиперболических функциях примут следующий вид:
(12.10)
Для вывода этих формул достаточно в предыдущей системе уравнений произвести обратную замену l на y. Эту запись удобно использовать для исследования режимов работы линии при изменении сопротивления нагрузки
12.2.4. Линия без искажений
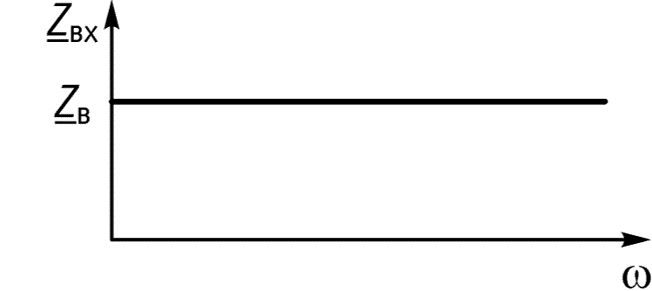
Если линия используется для передачи информации (линия связи, радио и т. п.), то для достоверности передачи необходимо, чтобы коэффициент затухания и волновое сопротивление линии не зависели от частоты. В этом случае, несмотря на затухание, форма передаваемого сигнала не будет изменяться и при согласованной нагрузке не возникнут отраженные волны. Если к тому же коэффициент фазы будет пропорционален частоте β = const·ω, то и фазовая скорость 
не будет зависеть от частоты. Такая линия называется линией без искажений и для выполнения выше перечисленных условий необходимо:
. (12.11)
Действительно, из (12.4) и (12.6) легко получить
(12.12)
(12.13)
Так что ни в волновое сопротивление 
, ни в коэффициент затухания 
частота не входит (это вещественные числа), а коэффициент фазы 
частоте пропорционален. Характерно, что оба коэффициента принимают в этом случае минимальные значения:
(12.14)
Фазовая скорость волн в линии достигает в этом случае наибольшего значения:
. (12.15)
Если линия работает в режиме согласованной нагрузки, то в линии существует только одна волна, поэтому в любой точке линии в любой момент времени 
причем ток и напряжение совпадают по фазе.
Следует иметь в виду, что как у воздушных, так и у кабельных линий 
поэтому для выполнения условия (12.11) приходится включать через равные расстояния дополнительную сосредоточенную индуктивность. Правда, при этом уменьшается скорость распространения волн в линии.
Известны первичные параметры линии связи:
Определить, какую дополнительную индуктивность нужно включать через каждый километр линии, чтобы сигналы по ней передавались без искажения.
Из условия (12.11) найдем, какой должна быть индуктивность единицы длины линии без искажения:
Поэтому 
мГн, где l = 1 км.
12.2.5. Линия без потерь
В некоторых практически важных случаях (особенно при высоких частотах в линиях связи, телевидения, радио) оказывается 
и можно для упрощения анализа пренебречь потерями в линии, приняв 
Тогда коэффициент затухания a = 0, коэффициент распространения 
– мнимое число, поэтому от гиперболических функций мнимого аргумента можно перейти к тригонометрическим функциям вещественного аргумента:
, 
.
Тогда и уравнения линии в гиперболических функциях (12.10) переходят в уравнения линии без потерь в тригонометрических функциях:
(12.16)
Здесь координата y отсчитывается от конца линии (рис. 12.3,б), причем, как в линии без искажений, волновое сопротивление линии без потерь 
– вещественное число, а фазовая скорость имеет наибольшее значение 
, которое в воздушных линиях достигает скорости света с = 300000 км/с. Длина волны 
.
Рассмотрим характерные режимы работы линии.
Холостой ход. 
При этих условиях уравнения (36.5) превращаются в
(12.17)
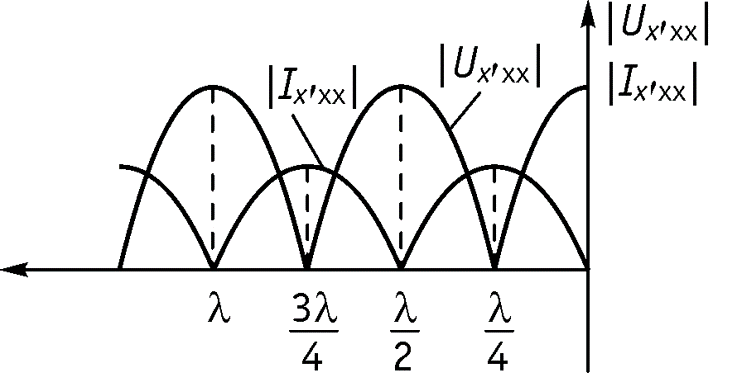
В результате наложения двух незатухающих волн одинаковой амплитуды, движущихся в противоположных направлениях, в линии существуют стоячие волны. Узлы напряжения соответствуют пучностям тока и оказываются в точках с координатами 
, 
, . а узлы тока и пучности напряжения – соответственно в точках 
, 
, l, .
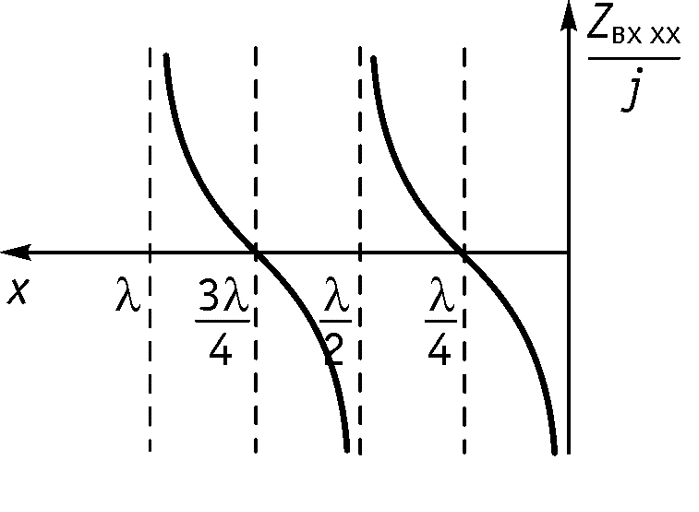
Входное сопротивление линии длиной l
(12.18)
имеет чисто реактивный характер. При 
, 
и т. д. оно емкостное, а при 
, 
и т. д. – индуктивное. При 
, и т. д. это сопротивление равно нулю (резонанс напряжений), а при 
, l и т. д. стремится к бесконечности (резонанс токов). Соответствующие кривые построены на рис. 12.4,а.
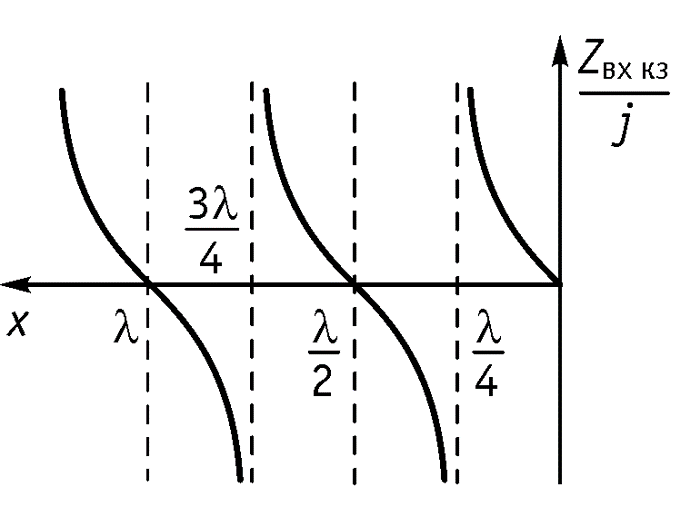
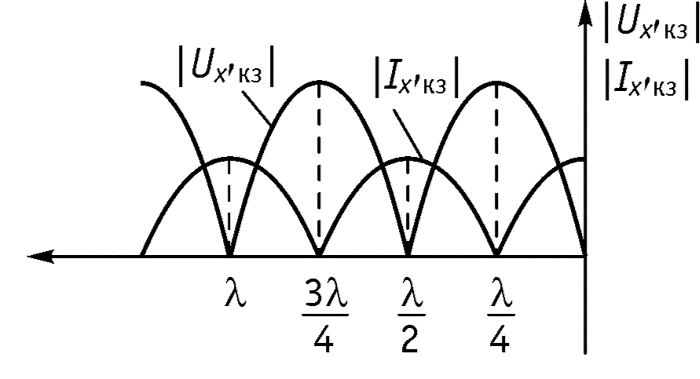
Короткое замыкание. 
N = –1.
. (12.19)
В этом режиме тоже существуют стоячие волны, но по сравнению с предыдущим случаем узлы и пучности токов и напряжений сдвинуты на четверть длины волны. Входное сопротивление
тоже чисто реактивное. Но его характер противоположен характеру 
в режиме холостого хода на тех же участках. Зависимости |U(y)|, |I(y)|, 
показаны на рис. 12.4,б.
где 
причем 
так что 
Поэтому
(12.21)
И здесь обнаружились стоячие волны, но узлы и пучности напряжения (тока) смещены в сторону увеличения y по отношению к их расположению в режиме короткого замыкания на расстояние 
при емкостной нагрузке и на расстояние, большее четверти длины волны, при индуктивной нагрузке. Соответствующий сдвиг имеет и график .
Три режима, рассмотренные выше, объединяет общее обстоятельство: отсутствует потребление энергии и в нагрузке, и в линии. Только в этом случае могут существовать точки, через которые не передается энергия – узлы тока и напряжения. На участках между этими точками осуществляется обмен энергией между электрическим и магнитным полями.
Известно, что высокочастотная линия с волновым сопротивлением 
Ом нагружена на чисто реактивный двухполюсник.
Определить величину и характер сопротивления нагрузки, если ближайший к концу линии узел тока находится на расстоянии 
м, а следующий за ним узел напряжения – на расстоянии 
м.
Расстояние между узлами тока и напряжения – это четверть длины волны. Поэтому 
м. В режиме реактивной нагрузки 
рад/с, и 
. Значит, линия нагружена на индуктивность. Тогда 
Ом.
где 
(12.22)
Проанализировав эти выражения, можно заметить, что ни кривая U(y), ни кривая I(y) не имеют ни узлов, ни пучностей при любых 
хотя и сохраняют волнообразный характер (рис. 12.5). При 
максимумы напряжения и минимумы тока лежат в тех же точках, что и пучности напряжения и узлы тока в режиме холостого хода. В данном случае максимум действующего значения напряжения 
А минимум напряжения отстоит от конца линии на расстоянии 
и, как следует из (12.22), 
В радиотехнике вводится понятие коэффициента бегущей волны как отношения этих величин 
Так что при 
оказывается 
Если же 
то минимумы напряжения и максимумы тока расположены там же, где пучности тока и узлы напряжения в режиме короткого замыкания. Поэтому в конце линии 
а на расстоянии от конца линии лежит точка, в которой 
Значит, при 
получится 
Так что по распределению напряжения в линии с известным волновым сопротивлением нетрудно вычислить и сопротивление нагрузки.
Естественно, наибольшее значение 
достигается в режиме согласованной нагрузки, когда в линии существует только одна бегущая волна, которая не отражается от нагрузки.
Согласованная нагрузка. 
(12.11)
Действующие значения тока и напряжения во всех точках линии одинаковы (рис. 12.5), причем мгновенные значения этих величин совпадают по фазе.
Линия без потерь длиной обладает весьма полезными для практического использования свойствами. Для нее 
, тогда
В режиме короткого замыкания входное сопротивление линии стремится к бесконечности, то есть четвертьволновая линия представляет собой идеальный изолятор.
В режиме активной нагрузки четвертьволновую линию можно рассматривать как «трансформатор сопротивлений» и применять для согласования генератора с внутренним сопротивлением и приемника с сопротивлением . Параметры линии следует подобрать таким образом, чтобы Тогда входное сопротивление пассивного двухполюсника, подключенного к генератору (система линия–нагрузка), а эквивалентное внутреннее сопротивление активного двухполюсника (система генератор–линия), к которому подключена нагрузка, равно При таком подборе параметров генератор будет выдавать за период максимально возможную энергию, причем вся эта энергия перейдет в нагрузку, поскольку потери в линии отсутствуют. Аналогичное условие используется для согласования двух линий с разными волновыми сопротивлениями 
и 
при помощи третьей (четвертьволновой) линии, включенной между ними. Ее волновое сопротивление должно быть 
.
12.3. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ
С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
12.3.1. Прямая и обратная волны
В линиях электропередачи, связи, обмотках трансформаторов и других цепях с распределенными параметрами переходные процессы возникают чаще всего по тем же причинам, что и в цепях с сосредоточенными параметрами. Это может быть подключение цепи к источнику и отключение от него, подключение нагрузки и ее отключение, скачкообразное изменение параметров какого-либо участка цепи (например, в случае аварии). Кроме того, при достаточной протяженности цепи переходные процессы могут возникнуть и в случае изменения электромагнитных полей в окружающем пространстве (например, во время грозы). Токи и напряжения во время переходных процессов зависят от двух переменных – времени t и расстояния x. Переходные процессы имеют волновой характер.
Ниже рассматриваются примеры переходных процессов в однородной двухпроводной линии без потерь 
Из (12.1) следуют уравнения линии без потерь в частных производных:
(12.24)
Решим их операторным методом, подобно тому, как в разделе 12.2.1 решали уравнения (12.1) комплексным методом.
Пусть 
, 
– операторные изображения соответствующих функций времени 
, 
. Тогда в соответствии с теоремой дифференцирования можно найти изображения частных производных тех же величин при нулевых начальных условиях 
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать
Гиперболическая форма уравнений длинной линии
Гиперболическая форма уравнений длинной линии (ДЛ) имеет следующий вид (после применения формул Эйлера для решения уравнений длинной линии с использованием падающей и отраженной волн)
U ( x ) = U 2 c h γ x + I 2 Z В s h γ x ; I ( x ) = U 2 Z В s h γ x + I 2 c h γ x ,
что соответствует гиперболической форме уравнений симметричного четырехполюсника
U 1 = U 2 c h γ + I ′ 2 Z C s h γ ; I 1 = U 2 Z C s h γ + I ′ 2 c h γ .
Поскольку I’2 соответствует току I2 ДЛ, волновое сопротивление ZB = ZC соответствует характеристическому сопротивлению четырехполюсника, а характеристическая мера передачи четырехполюсника γ соответствует γ·l.
Здесь l – длина длинной линии; x – координата длинной линии, отсчитанная от ее конца (нагрузки); U1, I1 и U2, I2 – переменные входа и выхода длинной линии.
Таким образом, длинной линии – симметричный четырехполюсник.
Гиперболическая форма уравнений, длинная линия
Видео:Установившийся режим в однородной линии. Уравнение однородной линии с гиперболическими функциями.Скачать
Цепи с распределенными параметрами. Однородные линии. Уравнения передачи однородной линии
Страницы работы
Содержание работы
XVIII Цепи с распределенными параметрами
18.1 Однородные линии
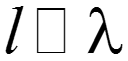
Электрическая цепь, у которой геометрические размеры соизмеримы с длинной волны ( ) и у которых индуктивность, емкость, сопротивление и проводимость распределены по длине, называется электрической цепью с распределенными параметрами.
Если геометрические размеры электрической цепи намного меньше длины волны ( ), то такая электрическая цепь называется цепью с сосредоточенными параметрами. Условие – условие квазистационарности
Если только один из размеров не удовлетворяет условию , то такая цепь называется длинной линией. Различают: однородные и неоднородные длинные линии.
- Однородные длинные линии – это линии, у которых параметры неизменны при изменении расстояния.
- Неоднородные линии – это линии, у которых параметры изменяются с изменением расстояния.
Первичные параметры однородной длинной линии.
равны значениям соответствующих распределенных параметров, измеренных на отрезке линии единичной длины (1 км для линии проводной связи и 1 м для линии радиосвязи).
К первичным параметрам относятся:
–сопротивление R; –проводимость G; – индуктивность L; – емкость С.
Вторичные параметры длинной линии
- Волновое сопротивление линии, [Ом].
Для однородной линии, рассматриваемой между выходными и входными выводами как симметричный четырехполюсник, волновое сопротивление равно характеристическому сопротивлению .
2. Коэффициент распространения
– коэффициент ослабления длинной линии [Нп/км], [Нп/м] или [ДБ/км], [ДБ/м];
Характеризует изменение тока и напряжения по абсолютной величине на единицу длины
— собственное ослабления линии [Нп] или [ДБ];
Ослабление сигнала на расстоянии х от начала линии
– коэффициент фазы [рад/км], [рад/м], [градус/км], [градус/м].
Характеризует изменение тока и напряжения по фазе на единицу длины
— собственная фаза линии [рад], [градус].
18.2 Уравнения передачи однородной линии
- Напряжение и ток в любой точке линии является функцией времени t и расстояния х
- Выделим отрезок линии длиной х и представим эквивалентную схему длинной линии с выделенным участком х на расстоянии х от генератора
Телеграфные уравнения длинной линии
Для установившегося гармонического колебания телеграфные уравнения имеют вид
Для решения телеграфных уравнений необходимо разделить переменные (U и I). Для этого продифференцируем уравнения по х. В полученные уравнения подставим вместо и их выражения из системы уравнений для установившегося гармонического колебания
Волновые уравнения длинной линии
Поскольку волновые уравнения – линейные дифференциальные однородные уравнения 2-го порядка, то их решение в произвольном сечении х находится в виде
– постоянные интегрирования, определяемые из граничных условий, в качестве которых обычно используют напряжение и ток, либо в начале линии ( и при х = 0), либо ток и напряжение в конце линии ( и при х = ).
Решение для тока, как правило, выражают через найденное напряжение
Определяем постоянные интегрирования из системы уравнений для напряжения и тока при x = 0
Уравнения передачи в гиперболической форме
Уравнения передачи в начале линии , через напряжение и ток в конце линии
Уравнение передачи в конце линии , через напряжение и ток в начале линии
18.3 Волновые процессы в однородной длинной линии
В линиях с потерями ( 0) рассматривают бегущие затухающие прямые и обратные волны и их суперпозиции. Бегущая волна – волна, перемещающаяся вдоль линии.
Прямая бегущая волна – волна, перемещающаяся от начала к концу линии. Обратная бегущая волна – волна, перемещающаяся от конца к началу линии
Падающая волна – прямая бегущая волна. Отраженная волна – частный случай обратной бегущей волны, возникающей в результате неравенства волнового сопротивления линии и сопротивления нагрузки ( ).
Уравнения передачи для мгновенных значений в любом сечении
Соотношения между волнами в начале (x = 0) и в конце (x = l) линии
Длина волны – расстояние между ближайшими точками х1 и х2, взятое в направлении распространения волны, фазы колебания в которых отличаются на 2.
Фазовая скорость – скорость перемещения фазы колебания
За один период колебания бегущая волна проходит расстояние, равное длине волны
Коэффициент отражения по напряжению (току) –отношение комплексной амплитуды отраженной волны напряжения (тока) к комплексной амплитуде падающей волны напряжения (тока).
показывает, какую часть комплексной амплитуды падающей волны составляет комплексная амплитуда отраженной волны
Коэффициенты отражения по напряжению и по току в начале линии
Коэффициенты отражения по напряжению и по току в конце линии
Режим согласованного включения
- В линии – только падающие волны
- Нет эхо-сигналов — нет искажений
- Минимальное рабочее ослабление
Линия без искажений
Линия, на приемном конце которой сохраняется форма передаваемого сигнала
Для такой передачи необходимо:
- Ослабление и фазовая скорость – постоянны
2. 3. Линия согласованно нагружена
Подберем первичные параметры так, чтобы — условие Хевисайда
Для реальных линий обычно
Уменьшение R – увеличение диаметра провода (дорого)
Уменьшение С – увеличение расстояния между проводами (не всегда возможно)
Увеличение G – рост затухания
Лучше всего – искусственное увеличение L
При передаче ВЧ сигнала автоматически получается линия без искажений
18.4 Волновые процессы длинной линии без потерь
Такая линия, для которой (для небольших линий на СВЧ)
Входное сопротивление линии
1. Согласованный режим работы в длинной линии без потерь
Режим бегущей волны
- Амплитуды колебаний постоянны
- Сдвиг фаз между током и напряжением равен нулю
- Мощность имеет активный характер
2. Режим короткого замыкания
Уравнение стоячей волны
Амплитуды напряжения и тока являются функциями координаты х
Нулевое значение – узел стоячей волны Максимальное значение – пучность стоячей волны
Стоячие волны возникают в длинной линии без потерь при условии, когда к длинной линии подключена нагрузка, модуль коэффициента отражения которой равен 1, при этом амплитуды падающей и отраженной волн напряжения (тока) переносят одинаковую мощность в прямом и обратном направлениях и энергия в нагрузке не потребляется.
3. Режим холостого хода
4. Линия, нагруженная на активное сопротивление, не равное волновому
— режим смешанных волн
Коэффициент бегущей волны
используется для оценки близости смешанной волны к режиму бегущей волны
Если , то в линии наступает режим стоячей волны, если , то в линии наступает режим бегущей волны.
🌟 Видео
Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать
Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать
Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать
14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать
ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать
Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать
Математика без Ху!ни. Уравнение плоскости.Скачать
Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать
Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать
ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать
Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать
Дифференциальное исчисление функции одной переменной. Часть 1Скачать
Алгоритмы. Линеаризация функцийСкачать
