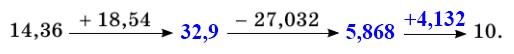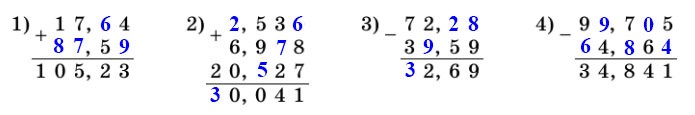Решение уравнений на сложение и вычитание десятичных дробей

Презентация была опубликована 9 лет назад пользователемschooltelman.ru

Похожие презентации

Видео:Математика 5 кл Сложение и вычитание десятичных дробейСкачать

Презентация на тему: » Сложение и вычитание десятичных дробей Решение уравнений.» — Транскрипт:

1 Сложение и вычитание десятичных дробей Решение уравнений

2 Цели: Отрабатывать умения и навыки сложения и вычитания десятичных дробей при решении уравнений. Задачи: Формировать умение и навыки данной темы. Развивать интерес к математике. Воспитывать аккуратность в записи.

3 Решение уравнений: Зная, что 11,87-7,39=4.48, найдите значение выражения или решите уравнение: а) 7,39 +4,48; б)х – 7,39 = 4,48; в)11,87 – 4,48; г) 7,39 + у = 11.87; д)4,48 + х = 11,87; е) 11,87 –р = 7,39.

4 Сказка «Волшебное слово» В некотором царстве, в некотором государстве жил-был Иван-царевич. Повстречал как-то Иван-царевич Елену Прекрасную. Они полюбили друг друга. Но злой Кощей Бессмертный похитил Елену Прекрасную. Иван-царевич поехал выручать свою любимую. Вот подъехал он к реке, а там огромный камень закрыл дорогу на мост. На камне написаны 3 уравнения: 1) (у – 3,71) — 5,46 = 12,77 2) (12,7 +х) – 9,8 = 3,2 3) (у +3,79) – 1,79 = 1,83. Если их правильно решить, то камень повернется и освободит дорогу. Помогите Ивану-царевичу

5 Царство Бабы Яги: -Долго ехал Иван – царевич по лесу, пока дорога не привела его к избушке Бабы Яги. Она давно враждовала с Кошем Бессмертным и согласилась помочь Ивану – царевичу, но только при условии,если он решит уравнения, написанные на стенах избушки

6 Решите уравнения 1) 6,5 + 2х = 14,5 2)12,4 – 3х = 3,4 3) 7,5 + 5х — 1,5 = 16 -Прощаясь с Иваном – царевичем,Баба Яга рассказала ему о силе корней уравнения: «Коль нужно тебе, какой запор отпереть или закрыть накрепко, произнеси вслух корни уравнения. Мигом исполнится».

7 Черный Ворон: Чёрный ворон подслушал этот разговор и рассказал обо всём Кощею. Тот подстерёг Ивана – царевича, схватил его и бросил в глубокое подземелье. Замкнул на 3 замка. Помогите Ивану – царевичу 1) 35 : х – 1,2 = 3.8 2) у : = 7,7 3)(х – 5,4) — 2,3 = 5,2

8 «Волшебные слова»: Иван-царевич произнёс «волшебные слова»,назвал корни всех уравнений. Двери подземелья открылись. И встал Иван – царевич перед воротами Кощеева царства. А на воротах написано уравнение: (у + 2,84) -1,84 =6,4 –Устно решил его Иван – царевич. Ворота открылись. Освободил Иван – царевич Елену Прекрасную и в тот же день сыграли они свадьбу. А вы сможете устно решить это уравнение

9 Из истории математики. –Правила вычислений с десятичными дробями описал знаменитый ученый аль — Каши Джемшид Ибн Масуд в начале XV века. Записывал он дроби так же, как принято сейчас, но не использовал запятой: дробную часть записывал красными чернилами или отделял вертикальной чертой. Но в Европе об этом не узнали и только через 150 лет учёный Симон Стивен записал десятичные дроби довольно сложно: в место запятой нуль в кружке. Запятая или точка для отделения целой части стали использоваться с XVII века. В России о десятичных дробях изложил Л. Ф. Магнитский в 1703 году в первом учебнике математики «Арифметика, сиречь наука числительная».

10 Выполните задание 1).2, ,01 = 2) 105,11 – 8,7 = 3)Решить уравнение: 1 – х = 0,89 4) Решить уравнение: х + 15,35 = 19,4 5)В первый день продали 12,52 м ткани, а во второй день ещё 19.7 м.Сколько ткани продали за два дня? 6). Масса двух кочанов капусты 10,67 кг, а одного из них 5,29 кг. Какова масса другого кочана?

11 Занимательная страница: п/пКСЧТИЯ 12,4463,22455,1554,215, , , ,20,110,151, , ,0510,830,75 57,1830, ,229,4332, ,2115,9614,2713,44,08

12 Ответ Чистяк – большой подснежник. Весной им питаются муравьи, его любят пчёлы. В народе его называют жабник. Растение становится ядовитым, когда зреют плоды.

13 Проверка знаний Вариант 1 Обязательная часть. 1). Вычислить: а)28.,7 + 1,53 б)75,4 – 4,23 2). Найти значение выражения: 8,3 + 4, – 1,25. Дополнительная часть: 3). От куска проволоки длиной 20м отрезали 4 куска: первый — длиной 1,7м,а каждый следующий – на полметра больше предыдущего. Определите длину оставшегося куска проволоки. Вариант 2 Обязательная часть. 1). Вычислите: а)32,9 + 3,61 б)10 -4,26. 2). Найдите значение выражения: , – Дополнительная часть 3). Маршрут состоит из 3 участков Первый участок имеет длину 4,2км,а второй – на полтора километра больше, а третий – на полтора километра меньше первого. Какова длина всего маршрута?

14 Задание на дом: 4. Задание на дом: 1241, 1242 (б).

Видео:Сложение и вычитание десятичных дробей. 5 класс.Скачать

Урок математики в 5 классе по теме «Сложение и вычитание десятичных дробей»
план-конспект урока по алгебре (5 класс) на тему

Цели и задачи урока:

Познавательные: научить решать уравнения с десятичными дробями; продолжить работу над текстовыми задачами;

Практические: развивать самостоятельность мышления, выражать свое мнение, выделять главное, делать выводы, развивать личностное саморазвитие учащихся, развивать умения и навыки вычислительного характера.

Метапредметные: воспитывать культуру общения, усидчивость, внимание и трудолюбие, формировать самостоятельность и активность, гуманных отношений на уроке.

Тип урока: комбинированный

Ожидаемые результаты:

Предметные: после проведения урока учащиеся будут решать уравнения и текстовые задачи с десятичными дробями.

Личностные: формировать внимательность и исполнительскую дисциплину.

Познавательные: давать качественные характеристики объектам в соответствии с их числовыми значениями.

Коммуникативные: оказывать в сотрудничестве необходимую помощь, аргументировать свою точку зрения.

Регулятивные: формировать креативность мышления, находчивость, умения анализировать и выстраивать логическую цепочку.

Формы организации деятельности учащихся: фронтальная, индивидуальная, групповая.

Оборудование: компьютер, мультимедийный проектор, презентация для сопровождения урока, индивидуальные карточки с заданиями, компьютерный тест.

План урока:

I. Организационный момент -1мин

II. Актуализация знаний и умений. – 5 мин.

III. Самоопределение к деятельности. – 3 мин.

IV. Работа по теме урока -10 мин.

V. Физкультминутка – 2 мин.

VI. Повторение изученного материала. – 7 мин.

VII. Самостоятельная работа (работа по карточкам +компьютерный тест) -10 мин

VIII. Домашнее задание- 1 мин.

IX. Рефлексия – 1 мин.

X. Подведение итогов урока -1 мин.

Видео:Уравнения с десятичными дробями в 5 классе (на сложение и вычитание).Скачать

Скачать:

Видео:Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать

Предварительный просмотр:

МБОУ Ямновская ООШ

Учитель: Шкуратова А.И.

Тема урока : Сложение и вычитание десятичных дробей.

Цели и задачи урока:

Познавательные: научить решать уравнения с десятичными дробями; продолжить работу над текстовыми задачами;

Практические: развивать самостоятельность мышления, выражать свое мнение, выделять главное, делать выводы, развивать личностное саморазвитие учащихся, развивать умения и навыки вычислительного характера.

Метапредметные: воспитывать культуру общения, усидчивость, внимание и трудолюбие, формировать самостоятельность и активность, гуманных отношений на уроке.

Тип урока : комбинированный

Предметные: после проведения урока учащиеся будут решать уравнения и текстовые задачи с десятичными дробями.

Личностные: формировать внимательность и исполнительскую дисциплину.

Познавательные : давать качественные характеристики объектам в соответствии с их числовыми значениями.

Коммуникативные: оказывать в сотрудничестве необходимую помощь, аргументировать свою точку зрения.

Регулятивные: формировать креативность мышления, находчивость, умения анализировать и выстраивать логическую цепочку.

Формы организации деятельности учащихся : фронтальная, индивидуальная, групповая.

Оборудование: компьютер, мультимедийный проектор, презентация для сопровождения урока, индивидуальные карточки с заданиями, компьютерный тест.

1. Организационный момент -1мин
2. Актуализация знаний и умений. – 5 мин.
3. Самоопределение к деятельности. – 3 мин.
4. Работа по теме урока -10 мин.
5. Физкультминутка – 2 мин.
6. Повторение изученного материала. – 7 мин.
7. Самостоятельная работа (работа по карточкам +компьютерный тест) -10 мин
8. Домашнее задание- 1 мин.
9. Рефлексия – 1 мин.
10. Подведение итогов урока -1 мин.

1. Организационный момент (Создание благоприятного психологического настроя на урок).

Ну-ка, проверь дружок

Ты готов начать урок?

Всё ль на месте,

Всё ль в порядке,

Ручка, книжка и тетрадка?

Все ли правильно сидят?

Все ль внимательно глядят?

Каждый хочет получать

Только лишь оценку пять.

1. Актуализация знаний и умений.

День надо начинать с утренней гимнастики,

а урок математики- с гимнастики ума.

1. Индивидуальная работа у доски (2 уч-ся)

1)Вычисли удобным способом

— Найди правильный ответ и запусти в небо воздушный шар.

— Проверка индивидуальной работы

1. Представьте число 7 в виде дроби со знаменателем 4.

2. У наседки 18 цыплят. 34 всего количества- петушки. Сколько петушков у наседки?

3. Скорость течения реки 3,2 км/ч, а скорость теплохода 30 км/ч. Найдите скорость теплохода по течению.

Слайд № 22. Поставь в нужном месте запятые

3+ 108= 408; 736-336=4;

1. Самоопределение к деятельности.

• Посмотрите на записи. Что можете о них сказать?

— Дайте определение уравнению.

— Что значит решить уравнение?

— Какие числа используются в уравнениях?

Исходя из данных заданий можете ли вы сказать, чем мы будем заниматься на уроке?

Мы сегодня продолжим работу над темой «Сложение и вычитание десятичных дробей». Да, действительно задача нашего урока учиться решать уравнения с десятичными дробями, а также продолжить работу над текстовыми задачами.

— Как вы думаете, каким образом, решаются уравнения с десятичными дробями?

(Они решаются так же, как и с обыкновенными дробями и натуральными числами. При решении используется связь между компонентами и результатами арифметических действий)

— Давайте решим уравнение у доски (коллективное выполнение у доски с объяснением)

6,7 –X = 2,8 Какой компонент неизвестен?

X =6,7 – 2,8 Как найти вычитаемое?

X= 3,9 ( из уменьшаемого вычесть разность)

— Выполните уравнение Y – 2,7 = 3,4 самостоятельно Самопроверка. Сравни с

решением на слайде

— Решение уравнения у доски (коллективное выполнение у доски с объяснением)

(X + 3,5) – 4,8 = 2,4; Какой компонент неизвестен?

X+ 3,5 =2,4 + 4,8 Как найти уменьшаемое?

X+3,5= 7,2 ( из уменьшаемого вычесть разность)

X= 7,2 – 3,5 Какой компонент неизвестен?

X = 3,7 (первое слагаемое)

(3,7 + 3,5) – 4,8 = 2,4; Как найти первое слагаемое?

Ответ: 3,7 ( из суммы вычесть второе слагаемое )

— Выполнение уравнений самостоятельно 1 –В (7,1 – X) + 3,9 = 4,5;

Видео:Уравнения с десятичными дробями. Математика 5 классСкачать

Мерзляк 5 класс — § 33. Сложение и вычитание десятичных дробей

Вопросы к параграфу

1. Сформулируйте правило сложения десятичных дробей.

Чтобы сложить две десятичные дроби, надо:

1. уравнять слагаемые в количестве цифр после запятой;
2. записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
3. сложить полученные числа так, как складывают натуральные числа;
4. поставить в полученной сумме запятую под запятыми в слагаемых.

2. Сформулируйте правило вычитания десятичных дробей.

Чтобы из одной десятичной дроби вычесть другую, надо:

1. уравнять в уменьшаемом и вычитаемом количестве цифр после запятой;
2. записать уменьшаемое и вычитаемое так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
3. произвести вычитание так, как вычитают натуральные числа;
4. поставить в полученной разности запятую под запятыми в уменьшаемом и вычитаемом.

Решаем устно

1. Какая из следующих десятичных дробей равна дроби .

1. 0,79000
2. 0,0079
3. 0,00079 — десятичная дробь, равная заданной
4. 0,7900

2. Какая из следующих десятичных дробей наибольшая:

1. 43,56
2. 43,561 — наибольшая десятичная дробь
3. 43,559
4. 43,55

3. Какое из следующих чисел получим, если округлим десятичную дробь 6,27 до десятых:

1. 6,2
2. 6,3 — округлённая до десятых десятичная дробь 6,27
3. 6,26
4. 6,28

4. На двух полках вместе на 20 книг больше, чем на каждой из них. Сколько книг на каждой полке?

Из условия следует, что:

• на первой полке книг на 20 меньше, чем на обеих полках вместе, то есть на второй полке находится 20 книг;
• на второй полке книг на 20 меньше, чем на обеих полках вместе, то есть на первой полке находится 20 книг.

Ответ: на каждой из полок по 20 книг.

5. Сравните:

Упражнения

863. Вычислите:

864. Выполните сложение:

865. Выполните сложение:

866. Выполните вычитание:

867. Выполните вычитание:

868. Решите уравнение:

869. Решите уравнение:

870. В декабре фермер получил прибыль в размере 438,86 тысячи рублей, а в январе — на 16,4 тысячи рублей больше, чем в декабре. Сколько тысяч рублей составила прибыль фермера за декабрь и январь вместе?

1) 438,86 + 16,4 = 455,26 (тыс. р.) — прибыль фермера в январе.

2) 438,86 + 455,26 = 894, 12 (тыс. р.) — прибыль фермера за январь и февраль.

Ответ: 894,12 тыс. рублей.

871. Баба-яга купила новую двухкомнатную избушку на курьих ножках. Площадь одной комнаты составляет 17,6 м², что на 5,9 м² меньше, чем площадь второй. Вычислите для Бабы-яги общую площадь двух её комнат.

1) 17,6 + 5,9 = 23,5 (м²) — площадь второй комнаты.

2) 17,6 + 23,5 = 41,1 (м²) — площадь двух комнат.

872. Собственная скорость теплохода равна 23,8 км/ч, скорость течения реки — 1,6 км/ч. Найдите скорость теплохода против течения и его скорость по течению реки.

1) 23,8 + 1,6 = 25,4 (км/ч) — скорость теплохода по течению реки.

2) 23,8 — 1,6 = 22, 2 (км/ч) — скорость теплохода против течения реки.

Ответ: по течению реки 25,4 км/ч, а против течения реки 22,2 км/ч.

873. Собственная скорость моторной лодки равна 16,4 км/ч, скорость течения — 1,8 км/ч. Найдите скорость лодки по течению и её скорость против течения реки.

1) 16,4 + 1,8 = 18,2 (км/ч) — скорость лодки по течению реки.

2) 16,4 — 1,8 = 14,6 (км/ч) — скорость лодки против течения реки.

Ответ: по течению реки 18,2 км/ч, а против течения реки 14,6 км/ч.

874. Скорость катера по течению реки равна 30,2 км/ч, а скорость течения — 2,2 км/ч. Найдите собственную скорость катера и его скорость против течения.

1) 30,2 — 2,2 = 28 (км/ч) — собственная скорость катера.

2) 28 — 2,2 = 25, 8 (км/ч) — скорость катера против течения.

Ответ: собственная скорость катера 28 км/ч, а скорость катера против течения — 25,8 км/ч.

875. Скорость катера на подводных крыльях против течения реки равна 68,5 км/ч, а скорость течения — 1,5 км/ч. Найдите собственную скорость катера и его скорость по течению.

1) 68,5 + 1,5 = 70 (км/ч) — собственная скорость катера на подводных крыльях.

2) 70 + 1,5 = 71,5 (км/ч) — скорость катера на подводных крыльях по течению реки.

Ответ: собственная скорость — 70 км/ч, скорость по течению реки — 71,5 км/ч.

876. Скорость лодки против течения реки равна 18,8 км/ч, а её собственная скорость — 20,2 км/ч. Найдите скорость течения и скорость лодки по течению реки.

1) 20,2 — 18,8 = 1,4 (км/ч) — скорость течения реки.

2) 20,2 + 1,4 = 21,6 (км/ч) — скорость движение лодки по течению реки.

Ответ: скорость течения реки — 1,4 км/ч, а скорость движения по течению — 21,6 км/ч.

877. Скорость катера по течению реки равна 32,6 км/ч, а его собственная скорость — 30,4 км/ч. Найдите скорость течения и скорость катера против течения реки.

1) 32,6 — 30,4 = 2,2 (км/ч) — скорость течения реки.

2) 30,4 — 2,2 = 28, 2 (км/ч) — скорость движения против течения.

Ответ: скорость течения реки — 2,2 км/ч, а скорость движения против течения — 28,2 км/ч.

878. Лена и Оля собрали вместе 3,2 кг грибов, причём Лена собрала 1,68 кг. Кто из девочек собрал больше грибов и на сколько килограммов?

1) 3,2 — 1,68 = 1,52 (кг) — грибов собрала Оля.

2) 1,68 > 1,52 — значит Лена собрала грибов больше, чем Оля.

3) 1,68 — 1,52 = 0,16 (кг) — грибов Лена собрала больше, чем Оля.

Ответ: Лена собрала на 0,16 кг грибов больше, чем Оля.

879. В первый день туристы прошли 6,3 км, что на 2,84 км меньше, чем во второй день. После двух дней похода им осталось пройти ещё 14,35 км. Какова протяжённость туристского маршрута?

1) 6,3 + 2,84 = 9,14 (км) — прошли туристы во второй день.

2) 6,3 + 9,14 = 15,44 (км) — прошли туристы в первые два дня.

3) 15,44 + 14,35 = 29,79 (км) — протяжённость маршрута.

880. За первую неделю магазин продал 2,16 т картофеля, а за вторую — на 0,976 т больше, чем за первую. После этого в магазине ещё осталось 3,58 т картофеля. Сколько тонн картофеля было завезено в магазин?

1) 2,16 + 0,976 = 3,136 (т) — картофеля продали за вторую неделю.

2) 2,16 + 3,136 = 5, 296 (т) — картофеля продали за две недели.

3) 5,296 + 3,580 = 8,876 (т) — картофеля было завезено в магазин.

881. Найдите общую площадь пустынь на поверхности земного шара, если площадь пустынь в Австралии равна 0,4 млн км², в Америке — на 1,2 млн км² больше, чем в Австралии, в Азии — на 1,4 млн км² больше, чем в Америке, а в Африке — на 2,8 млн км² больше, чем в Америке.

1) 0,4 + 1,2 = 1,6 (млн км²) — площадь пустынь в Америке.

2) 1,6 + 1,4 = 3 (млн км²) — площадь пустынь в Азии.

3) 1,6 + 2,8 = 4,4 (млн км²) — площадь пустынь в Африке.

4) 0,4 + 1,6 + 3 + 4,4 = 2 + 3 + 4,4 = 5 + 4,4 = 9,4 (млн км²) — общая площадь пустынь.

Ответ: 9,4 млн км².

882. Наибольшее озеро в мире — Каспийское море — имеет глубину 1,025 км. Озеро Байкал — самое глубокое в мире. Его глубина на 0,515 км больше глубины Каспийского моря. Глубина озера Танганьика (Африка) составляет 1,47 км. На сколько Байкал глубже Танганьики, а Танганьика глубже Каспийского моря?

1) 1,025 + 0,515 = 1,540 (км) — глубина озера Байкал.

2) 1,470 — 1,025 = 0,445 (км) — озеро Танганьика глубже Каспийского моря.

3) 1,54 — 1,47 = 0,07 (км) — озеро Байкал глубже озера Танганьика.

Ответ: Байкал глубже Танганьики на 0,007 км, а Танганьика глубже Каспийского моря на 0,445 км.

883. Отправившись на ядре в путешествие на Луну, барон Мюнхгаузен в первую минуту пролетел 234,7 км, что на 18,6 км меньше, чем во вторую минуту. В третью минуту он пролетел на 156,4 км меньше, чем в первую и вторую минуты вместе. Сколько километров пролетел Мюнхгаузен за первые три минуты полёта?

1) 234,7 + 18,6 = 253,3 (км) — пролетел за вторую минуту.

2) 234,7 + 253,3 = 488 (км) — пролетел за первые две минуты.

3) 488 — 156,4 = 331,6 (км) — пролетел за третью минуту.

4) 488 + 331,6 = 819,6 (км) — пролетел за первые три минуты.

884. В понедельник в столовой израсходовали 12,4 кг сахара, что на 2,8 кг больше, чем во вторник. В среду сахара было израсходовано на 5,6 кг меньше, чем в понедельник и во вторник вместе. Сколько всего килограммов сахара израсходовали в понедельник, вторник и среду?

1) 12,4 — 2,8 = 9,6 (кг) — сахара израсходовали во вторник.

2) 12,4 + 9,6 = 22 (кг) — сахара израсходовали в понедельник и вторник.

3) 22 — 5,6 = 16,4 (кг) — сахара израсходовали в среду.

4) 22 + 16,4 = 38,4 (кг) — сахара израсходовали в понедельник, вторник и среду.

885. За три дня на шахте добыли 2 436,86 т угля. За первый день добыча составляла 827,48 т, а за второй — на 59,59 т меньше, чем за первый. Сколько тонн угля добыли за третий день?

1) 827,48 — 59,59 = 767,89 (т) — угля добыли во второй день.

2) 827,48 + 767,89 = 1 595,37 (т) — угля добыли в первые два дня.

3) 2 436,86 — 1 595,37 = 841,49 (т) — угля добыли в третий день.

886. Фермер Василий Работящий взял в аренду три участка земли общей площадью 3 428,32 га. Площадь одного из этих участков была равна 1 506,46 га, что на 237,64 га меньше площади второго участка. Найдите площадь третьего участка.

1) 1 506,46 + 237,64 = 1 744,10 (га) — площадь второго участка.

2) 1 506,46 + 1 744,10 = 3 250,56 (га) — площадь первого и второго участка вместе.

3) 3 428,32 — 3 250,56 = 177,76 (га) — площадь третьего участка.

887. Ломаная состоит из трёх звеньев. Длина первого звена 9,2 см, что на 3,5 см больше длины второго звена и на 4,9 см меньше длины третьего. Найдите длину ломаной.

1) 9,2 — 3,5 = 5,7 (см) — длина второго звена.

2) 9,2 + 4,9 = 14,1 (см) — длина третьего звена.

3) 9,2 + 5,7 + 14,1 = 29 (см) — длина ломаной.

888. Одна из сторон треугольника равна 12,4 дм, что на 3,8 дм меньше второй стороны и на 2,6 дм больше третьей. Вычислите периметр треугольника.

1) 12,4 + 3,8 = 16,2 (дм) — длина второй стороны треугольника.

2) 12,4 — 2,6 = 9,8 (дм) — длина третьей стороны треугольника.

3) 12,4 + 16,2 + 9,8 = 38,4 (дм) — периметр треугольника.

889. Найдите значение выражения:

890. Найдите значение выражения:

891. Решите уравнение:

892. Решите уравнение:

893. Выполните сложение, выбирая удобный порядок вычислений:

1) (2,45 + 0,276) + 4,55 = (2,45 + 4,55) + 0,276 = 7 + 0, 276 = 7,276

2) (9,37 + 13,6) + 6,4 = 9,37 + (13,6 + 6,4) = 9,37 + 20 = 29,37

3) 5,12 + 3,75 + 5,25 + 4,88 = (3,75 + 5,25) + (5,12 + 4,88) = 9 + 10 = 19

4) 0,234 + 0,631 + 0,766 + 0,369 = (0,234 + 0,766) + (0,631 + 0,369) = 1 + 1 = 2

894. Выполните сложение, выбирая удобный порядок вычислений:

1) (12,82 + 8,394) + 5,18 = (12,82 + 5,18) + 8,394 = 18 + 8,394 = 26,394

2) 2,53 + 15,1 + 4,47 + 14,9 = (2,53 + 4,47) + (15,1 + 14,9) = 7 + 30 = 37

895. Упростите выражение:

1) 2,46 + а + 81,139 + 14,8 = ( 2,46 + 81,139 + 14,8) + а = 98,399 + а

2) m + 0,47 + 5,062 + m + 43,295 = (m + m) + (0,47 + 5,062 + 43,295) = 2m + 48.827

3) х + 0,3 + 0,9007 + 4,58 + 3x = (x + 3x) + (0,3 + 0,9007 + 4,58 ) = 4x + 5,7807

4) 7c + 236,7 + 2c + 0,82 + 4,325 = (7c + 2c) + (236,7 + 0,82 + 4,325) = 9c + 241,845

896. Найдите числа, которых не хватает в цепочке вычислений:

a = 14,36 + 18,54 = 32,9

b = 32,9 — 27,032 = 5,868

x = 10 — 5,868 = 4,132

897. Найдите числа, которых не хватает в цепочке вычислений:

a = 39,8 — 14,48 = 25,32

x = 74,123 — 25,32 = 48,803

y = 74,123 — 40,2 = 33,923

898. Вместо звёздочек поставьте цифры так, чтобы сложение (вычитание) было выполнено верно:

899. Как изменится сумма, если:

1) одно из слагаемых увеличить на 6,8, а второе — на 4,25

6,8 + 4,25 = 11,05 — сумма увеличится на 11,5.

2) одно из слагаемых увеличить на 14,3, а второе уменьшить на 7,15

14,3 — 7,15 = 7,15 — сумма увеличится на 7,15.

3) одно из слагаемых увеличить на 3,2, а второе уменьшить на 3,2?

3,2 — 3,2 = 0 — сумма не изменится.

900. Как изменится разность, если:

1) уменьшаемое увеличить на 9,25

разность увеличится на 9,25

2) уменьшаемое уменьшить на 7,6

разность уменьшится на 7,6

3) вычитаемое увеличить на 12,2

разность уменьшится на 12,2

4) вычитаемое уменьшить на 17,96

разность увеличится на 17,96

5) уменьшаемое увеличить на 0,4, а вычитаемое — на 0,3

0,4 — 0,3 = 0,1 — разность увеличится на 0,1

6) уменьшаемое увеличить на 2,3, а вычитаемое уменьшить на 1,7

2,3 + 1,7 = 4 — разность увеличится на 4

7) уменьшаемое уменьшить на 6,1, а вычитаемое увеличить на 3,4

6,1 + 3,4 = 9,5 разность уменьшится на 9,5

901. Выразите данные величины в дециметрах и выполните действия:

1) 2,34 дм — 18 см = 2,34 дм — 1,8 дм = 0,54 дм

2) 9,6 дм + 4 см = 9,6 дм + 0,4 дм = 10 дм

3) 49 дм — 324 см 49 дм — 32,4 дм = 16,6 дм

4) 5,63 м + 2 345 см = 56,3 дм + 234,5 дм = 290,8 дм

5) 9 м 8 дм 3 см — 25 см 8 мм = 98,3 дм — 2,58 дм = 95,72 дм

6) 1 м 5 дм 6 см — 16 см 9 мм = 15,6 дм — 1,69 дм = 13,91 дм

902. Выразите данные величины в арах и выполните действия:

1) 3 а 82 м² + 8 а 9 м² = 3,52 а + 8,09 а = 11,91 а

2) 28 а 7 м² + 14 а 26 м² =28,07 а + 14,26 а = 42,33 а

3) 57 а 22 м² — 48 а 4 м² = 57,22 а + 48,04 а = 10526 а

4) 41 а 5 м² — 36 а 19 м² = 4105 а — 36,19 а = 4,86 а

5) 9 га 6 а 8 м² + 18 а 10 м² = 906,08 а + 18,10 а = 924,18 а

6) 24 га 8 а 4 м² — 24 а 20 м² = 2408,04 а — 24,2 а = 2383,84 а

903. Выразите данные величины в центнерах и выполните действия:

1) 9 ц — 524 кг = 9 ц — 5,24 ц = 3,76 ц

2) 8 ц 44 кг — 836 кг = 8,44 ц — 8,36 ц = 0,08 ц

3) 42 ц 5 кг + 85 кг = 45,05 ц + 0,85 ц = 42,9 ц

4) 2,92 т + 684 кг = 29,2 ц + 6,84 ц = 36,04 ц

5) 7 т 6 ц 4 кг — 8 ц 18 кг = 7604 ц — 8,18 ц = 67,86 ц

6) 1 т 2 ц 3 кг — 1 т 15 кг = 12,03 ц — 10,15 ц = 1,88 ц

904. Найдите значение выражения, выбирая удобный порядок вычислений:

1) (4,12 + 0,116) — 1,12 = (4,12 — 1,12) + 0,116 = 3 + 0,116 = 3,116

2) (5,93 + 67,5) — 27,5 = 5,93 + (67,5 — 27,5) = 5,93 + 40 = 45,93

3) 0,844 — (0,244 + 0,018) = (0,844 — 0,244) — 0,018 = 0,600 — 0,018 = 0, 582

4) 7,29 — (3,961 + 2,29) = (7,29 — 2,29) — 3,961 = 5,000 — 3,961 = 1,039

Упражнения для повторения

905. От двух пристаней, расстояние между которыми равно 24 км, одновременно в одном направлении отчалили лодка и катер (лодка двигалась впереди катера). Скорость лодки равна 8 км/ч и составляет скорости катера. Через сколько часов после начала движения катер догонит лодку?

1) 8 : 4 • 5 = 2 • 5 = 10 (км/ч) — скорость катера.

2) 10 — 8 = 2 (км/ч) — скорость сближения катера и лодки.

3) 24 : 2 = 12 (ч) — катер догонит лодку.

Ответ: через 12 часов.

906. Длина бассейна равна 12 м, ширина его составляет длины, а глубина — ширины. Водой было наполнено объёма бассейна. Сколько кубических метров воды налили в бассейн?

1) 12 : 4 • 3 = 3 • 3 = 9 (м) — ширина бассейна.

2) 9 : 3 • 2 = 3 • 2 = 6 (м) — глубина бассейна.

3) 12 • 9 • 6 = 108 • 6 = 648 (м³) — объем бассейна.

4) 648 : 18 • 11 = 36 • 11 = 396 (м³) — наполнено.

907. За шоколадку и четыре пирожных заплатили 414 р., а за такую же шоколадку и восемь таких пирожных — 750 р. Сколько рублей стоит шоколадка?

1) 750 — 414 = 336 (рублей) — стоят 4 пирожка, так как вторая покупка отличается от первой именно на 4 пирожка.

2) 414 — 336 = 78 (рублей) — стоит шоколадка, так как в первую покупку купили 1 шоколадку и 4 пирожка.

Ответ: 78 рублей.

Задача от мудрой совы

908. Хитрый Лисёнок предложил Петру Скупердяйкину: «Каждый раз, когда ты перейдёшь мост, который я заколдую, твои деньги удвоятся. За это будешь мне каждый раз отдавать 24 монеты».

Сделал Скупердяйкин так три раза и остался совсем без денег.

Сколько денег было у Петра до встречи с Хитрым Лисёнком?

1 способ — при помощи уравнения

Пусть х монет было у Скупердяйкина сначала. Тогда после перехода 1 моста стало (2х — 24) монет, после перехода второго моста стало ((2х — 24) • 2 — 24) монет, а после перехода третьего моста стало (((2х — 24) • 2 — 24) • 2 — 24) или 0 монет. Можем составить уравнение:

((2х — 24) • 2 — 24) • 2 — 24 = 0
((2х — 24) • 2 — 24) • 2 = 24
(2х — 24) • 2 — 24 = 24 : 2
(2х — 24) • 2 — 24 = 12
(2х — 24) • 2 = 12 + 24
(2х — 24) • 2 = 36
2х — 24 = 36 : 2
2х — 24 = 18
2х = 18 + 24
2х = 42
х = 42 : 2
х = 21 (монета) — была у Скупердяйкина вначале.

Ответ: 21 монета.

2 способ — от конца до начала

1) (0 + 24) : 2 = 24 : 2 = 12 (монет) — было до перехода через третий мост.

2) (12 + 24) : 2 = 36 : 2 = 18 (монет) — было до перехода через второй мост.

3) (18 + 24) : 2 = 42 : 2 = 21 (монета) — была до перехода через первый мост, то есть в самом начале.

📸 Видео

Решение уравнений, 6 классСкачать

ДЕСЯТИЧНАЯ ДРОБЬ | сложение десятичных дробей | вычитание десятичных дробейСкачать

Уравнение. 5 класс.Скачать

Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Сложение и вычитание рациональных чисел. 6 класс.Скачать

5 класс, 32 урок, Сложение и вычитание десятичных дробейСкачать

Решение уравнений с дробными числами в 6 классеСкачать

Уравнения с десятичными дробями в 5 классе (на умножение и деление).Скачать

Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать

Сложение и вычитание десятичных дробей.Скачать

Сложение и вычитание десятичных дробей. Практическая часть. 5 класс.Скачать

ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ 😉 #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

Уравнения с дробями. Как решать уравнения с дробями в 5 классе.Скачать

5 класс. Математика. Решение уравнений. Сложение и вычитание десятичных дробей.Скачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать