- Введение
- Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
- Методы решения систем нелинейных уравнений
- Выбор модельной функции
- Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
- Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
- Численные методы: решение нелинейных уравнений
- Метод деления пополам
- Метод Ньютона: теоретические основы
- Визуализация метода Ньютона
- Метод секущих
- Метод парабол
- Метод простых итераций
- Нахождение всех корней уравнения
- Алгоритм нахождения корня n-ной степени — Википедия
- Ссылки [ править | править код ]
- Геометрическая интерпретация метода Ньютона (метод касательных)
- Метод деления пополам
- User type
- Industry
- Метод золотого сечения
- 🔍 Видео
Введение
Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.
Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме 
Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

Обозначим через 


Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].
Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.
С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.
Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.
Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.
Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.
scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней
method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.
Методы решения систем нелинейных уравнений
Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.
В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

Определим матрицу Якоби:

Запишем(3) в виде:

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

где 

При использовании записи (6) метод Ньютона (5) соответствует выбору:
Система линейных уравнений (5) для нахождения нового приближения 
При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.
Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

Выбор модельной функции
Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:
Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Krylov method iteration = 4219
Optimize root time 7.239 seconds:
Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton iteration = 13
Newton method time 0.496 seconds
Решение для n=200:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds
Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:
Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds
Вывод: Программа работает и при изменении модельной функции.
Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500
Видео:Уравнение четвертой степениСкачать

Численные методы: решение нелинейных уравнений
Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.
В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.
В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.
Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения 

В простейшем случае у нас имеется функция 
Каждому значению x из этого отрезка мы можем сопоставить число 
Нам нужно найти такое значение 


Визуально нам нужно определить точку пересечения графика функции 
Видео:Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать

Метод деления пополам
Простейшим методом нахождения корней уравнения 
Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.
Алгоритм состоит в следующем.
Предположим, мы нашли две точки 




Поделим отрезок 

Тогда либо 

Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.
Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.
Заметьте, описанный алгоритм применим для любой непрерывной функции.
К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.
Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.
Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.
Видео:10 Численные методы решения нелинейных уравненийСкачать

Метод Ньютона: теоретические основы
Классический метод Ньютона или касательных заключается в том, что если 




Уравнение касательной к функции 

В уравнении касательной положим 

Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:
Сходимость метода касательных квадратичная, порядок сходимости равен 2.
Таким образом, сходимость метода касательных Ньютона очень быстрая.
Запомните этот замечательный факт!
Без всяких изменений метод обобщается на комплексный случай.
Если корень 
Упражнение 1. Найти с помощью метода касательных решение уравнения 
Упражнение 2. Найти с помощью метода касательных решение уравнения 
К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие 
Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.
Видео:Теорема БезуСкачать

Визуализация метода Ньютона
Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень 
1) функция y= f(x) определена и непрерывна при 
2) f(a)·f(b) 0. Таким образом, выбирается точка с абсциссой x0, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x0 сначала удобно выбирать один из концов отрезка.
Рассмотрим метод Ньютона на конкретном примере.
Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f ‘(x) = 2x > 0 и f »(x) = 2 > 0.
Уравнение касательной в общем виде имеет представление:
В нашем случае: y-y0=2x0·(x-x0). В качестве точки x0 выбираем точку B1(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B1, и обозначаем точку пересечения касательной и оси Ox точкой x1. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.
Точка пересечения касательной и оси Ox: x1 =
Рисунок 2. Результат первой итерации
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x1, получаем точку В2 =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В2, и обозначаем точку пересечения касательной и оси Ox точкой x2.
Точка пересечения касательной и оси Ox: x2 = 
Рисунок 3. Вторая итерация метода Ньютона
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x2, получаем точку В3 и так далее.
В3 = (
Рисунок 4. Третий шаг метода касательных
Первое приближение корня определяется по формуле:

Второе приближение корня определяется по формуле:

Третье приближение корня определяется по формуле:

Таким образом, i-ое приближение корня определяется по формуле:
Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e — до выполнения неравенства |xi—xi-1|
using namespace std;
float f(double x) //возвращает значение функции f(x) = x^2-2
float df(float x) //возвращает значение производной
float d2f(float x) // значение второй производной
int _tmain(int argc, _TCHAR* argv[])
int exit = 0, i=0;//переменные для выхода и цикла
double x0,xn;// вычисляемые приближения для корня
double a, b, eps;// границы отрезка и необходимая точность
cin>>a>>b; // вводим границы отрезка, на котором будем искать корень
cin>>eps; // вводим нужную точность вычислений
if (a > b) // если пользователь перепутал границы отрезка, меняем их местами
if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня
cout 0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ?
xn = x0-f(x0)/df(x0); // считаем первое приближение
cout eps) // пока не достигнем необходимой точности, будет продолжать вычислять
xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона
> while (exit!=1); // пока пользователь не ввел exit = 1
Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.
Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.
Рис. 4. Решение ошибки компиляции проекта
Мы будем искать корни у функции f(x) = x2-2.
Сначала проверим работу приложения на «неправильных» входных данных. На отрезке [3; 5] нет корней, наша программа должна выдать сообщение об ошибке.
У нас появилось окно приложения:
Рис. 5. Ввод входных данных
Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.
Рис. 6. Ошибка «На этом отрезке корней нет!»
Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».
Теперь проверим работу приложения на корректных входных данных. Введем отрезок [0; 2] и точность 0.0001.
Рис. 7. Вычисление корня с необходимой точностью
Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.
Чтобы выйти из приложения, введем «Exit?» => 1.
Видео:Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать

Метод секущих
Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:

Итерационный процесс имеет вид:
где 
Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.
Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня 
Эта замечательная величина называется золотым сечением:
Убедимся в этом, считая для удобства, что 
Таким образом, с точностью до бесконечно малых более высокого порядка
Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде 
После подстановки имеем: 
Для сходимости необходимо, чтобы 

Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.
Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое 

Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.
Такая процедура определения момента окончания итераций называется приемом Гарвика.
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Метод парабол
Рассмотрим трехшаговый метод, в котором приближение 



Для этого заменим, аналогично методу секущих, функцию 



В форме Ньютона она имеет вид:
Точка 

Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.
Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если 

Этот метод очень удобен для поиска корней многочленов высокой степени.
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод простых итераций
Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: 

Пусть 




По теореме Банаха существует и единственна неподвижная точка
Она может быть найдена как предел простой итерационной процедуры
где начальное приближение 

Если функция 

Таким образом, если производная меньше единицы, то 
Условие 



Рассмотрим уравнение: 
Если в качестве 




Однако можно в качестве 


Эти итерации сходятся к неподвижной точке для любого начального приближения 
Действительно, в первом случае 




Рассмотрим 
т.е. такой итерационный процесс всегда сходится.
Метод Ньютона представляет собой частный случай метода простых итераций.
Здесь 


то если 



Если 
Поскольку 
Таким образом, сходимость метода Ньютона очень быстрая.
Видео:11 класс, 3 урок, Уравнения высших степенейСкачать

Нахождение всех корней уравнения
Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно.
Чтобы найти другие корни, можно было бы брать новые стартовые точки и применять метод вновь, но нет гарантии, что при этом итерации сойдутся к новому корню, а не к уже найденному, если вообще сойдутся.
Для поиска других корней используется метод удаления корней.
Пусть 







Применяя тот или иной метод нахождения корней к функции 



Повторяя указанную процедуру, можно найти все корни 
Заметим, что когда мы производим деление на тот или иной корень 


Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции 
Мы рассмотрели решение уравнений только в одномерном случае, нахождение решений многомерных уравнений существенно более трудная задача.
Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Алгоритм нахождения корня n-ной степени — Википедия
Численные методы: решение нелинейных уравнений HTML
Видео:Метод хордСкачать

Ссылки [ править | править код ]
- Atkinson, Kendall E. (1989), An introduction to numerical analysis (2nd ed.), New York: Wiley, ISBN 0471624896 .
Видео:Решение уравнения третьей степени x³-9x-12=0Скачать

Геометрическая интерпретация метода Ньютона (метод касательных)
Пусть корень ξ уравнения f(x)=0 отделен на отрезке [a,b]. Предположим мы нашли (n-1)-ое приближение корня xn-1. Тогда n-ое приближение xn мы можем получить следующим образом. Положим
xn = xn-1 + hn-1 . (3.15)
Раскладывая в ряд f(x=ξ) в точке xn-1, получим
f(xn) = f(xn-1+hn-1) = f(xn-1) + f’(xn-1)hn-1=0
Отсюда следует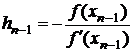
Подставим (3.16) в формулу (3.15), получим
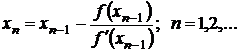
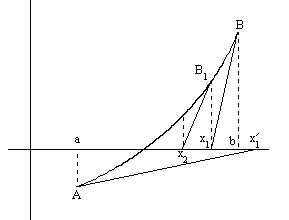
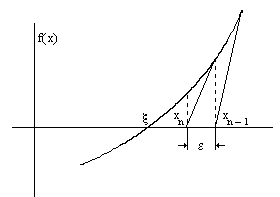
Рис.1. Геометрическая интерпретация метода Ньютона
Геометрически метод Ньютона эквивалентен замене дуги кривой y=f(x) касательной, проведенной в некоторой точке кривой (см. рис.1).
В точке B имеем f(x0)f’’(x0)>0. Здесь x0=b. Проведем касательную в точке B, получим на пересечении касательной осью OX точку x1. Далее проводим касательную в точке B1, получим точку x2 и т.д.
Если положить x0=a, то в точке x0 будем иметь f(x0)f’’(x0) 0 (3.18)
можно вычислить методом Ньютона (3.17) единственный корень ξ уравнения f(x)=0 с любой степенью точности.
Доказательство: Пусть f(a) 0, f′(x)>0, f″(x)>0, a≤x≤b. Согласно неравенству (3.18) в качестве точки x0 мы должны взять ту границу отрезка, для которой f(x0)>0, т.е. в данном случае т. b.
Итак, имеем x0>ξ. Докажем, что все приближения xn> ξ и следовательно все f(xn)>0. Пусть теперь xn-1> ξ. Положим ξ = xn-1 + (ξ-xn-1).
Применяя формулу Тейлора, получим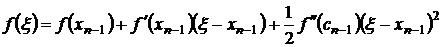
где ξ 0, то имеем
f(xn-1)+f′(xn-1)(ε-xn-1) x1> … >xn>xn+1>ε. Следовательно, существует 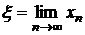
Переходя к пределу в формуле (3.17) получим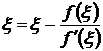
Оценим скорость сходимости метода Ньютона. Из (3.17) следует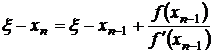
Представим f(ξ) в виде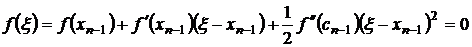
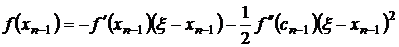
Подставим (3.21) в (3.20), получим
Отсюда 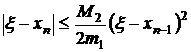
Здесь 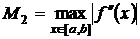
Таким образом, скорость сходимости метода Ньютона квадратичная.
Рис.2
Критерий завершения итерационного процесса имеет вид
|xn – xn-1| Пример . f(x) = x4-3×3+75x-10000=0.
Найти отрицательный корень с пятью верными знаками.
Решение: Полагая x=0, -10, -100, получим f(0)=-104, f(-10) = -150, f(-100) ≈ 108. Таким образом -100 0. Так как f(-11)f’’(-11)>0, то x0=-11.
Последовательные приближения даны в таблице.
| n | xn | f(xn) | f’(xn) | hn=- f(xn)/ f’(xn) |
| 0 | -11 | 3453 | -5183 | 0.7 |
| 1 | -10.3 | 134.3 | -4234 | 0.03 |
| 2 | -10.27 | 37.8 | -4196 | 0.009 |
| 3 | -10.261 | 0.2 | ||
| 4 | -10.260 | Шаг №1 – ограничение корней . Выясним, между какими числами расположен наш корень. Желательно, чтобы эти числа были кратны десяти: 10 2 = 100; 20 2 = 400; 30 2 = 900; … 90 2 = 8100; 100 2 = 10 000. Получили ряд чисел: 100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000. Эти числа – границы – диапазон, в котором лежит исходный корень. 2500 2 2 Видео:Вспоминаем схему Горнера и уравнения высших степенейСкачать  Метод деления пополамПростейшим методом нахождения корней уравнения Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом. Алгоритм состоит в следующем. Предположим, мы нашли две точки Поделим отрезок Тогда либо Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности. Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его. Заметьте, описанный алгоритм применим для любой непрерывной функции. К достоинствам метода деления пополам следует отнести его высокую надежность и простоту. Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений. Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень. Видео:Метод ЭйлераСкачать  User type
Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать  Industry
Видео:Метод неопределенных коэффициентовСкачать  Метод золотого сеченияТочки деления интервала выбираются таким образом, чтобы отношение длин подынтервалов удовлетворяло соотношению (см. рис.)
Так как Δk = Δk+1 + Δk+2, то имеем С учетом (3.32) из (3.33) получим уравнение корнем которого является золотое сечение. 🔍 ВидеоКак решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать  Численные методы - Занятие 1: Численное решение уравнения методом дихотомииСкачать  Численные методы - Занятие 2: Численное решение уравнения методом НьютонаСкачать  8 класс, 35 урок, Уравнения высших степенейСкачать  |




































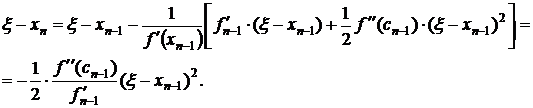
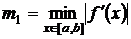
 50
50
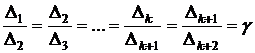
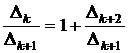 . (3.33)
. (3.33)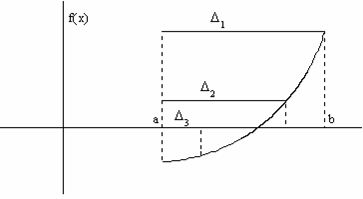
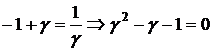
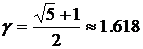 .
.