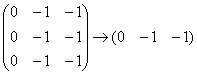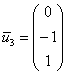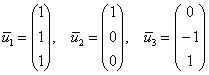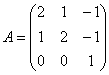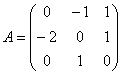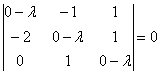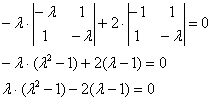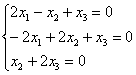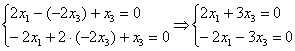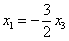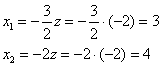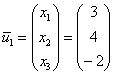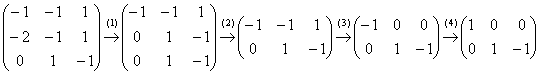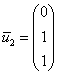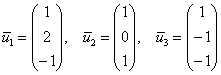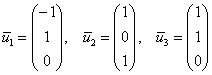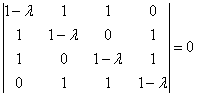Решение уравнений методом собственных векторов

При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:

Формула (2.6) определяет итерационный процесс, где начальное приближение [math]A^=A[/math] . На k-й итерации для некоторого выбираемого при решении задачи недиагонального элемента [math]a_^,

ine j[/math] , определяется ортогональная матрица [math]H^[/math] , приводящая этот элемент [math]a_^[/math] (а также и [math]a_^[/math] ) к нулю. При этом на каждой итерации в качестве [math]a_^[/math] выбирается наибольший по модулю. Матрица [math]H^[/math] называемая матрицей вращения Якоби, зависит от угла [math]varphi^[/math] и имеет вид

В данной ортогональной матрице элементы на главной диагонали единичные, кроме [math]h_^= cosvarphi^[/math] и [math]h_^=cosvarphi^[/math] , а остальные элементы нулевые, за исключением [math]h_^=-sinvarphi^[/math] , [math]h_^=sinvarphi^[/math] ( [math]h_[/math] -элементы матрицы [math]H[/math] ).

Угол поворота [math]varphi^[/math] определяется по формуле

где [math]|2varphi^|leqslant frac,

i ( [math]a_[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math] ).

В процессе итераций сумма квадратов всех недиагональных элементов [math]sigms(A^)[/math] при возрастании [math]k[/math] уменьшается, так что [math]sigms(A^) . Однако элементы [math]a_^[/math] приведенные к нулю на k-й итерации, на последующей итерации немного возрастают. При [math]ktoinfty[/math] получается монотонно убывающая ограниченная снизу нулем последовательность sigma(A^)> ldots> sigma(A^)>ldots»>[math]sigma(A^)> sigma(A^)> ldots> sigma(A^)>ldots[/math] . Поэтому [math]sigma(A^)to0[/math] при [math]ktoinfty[/math] . Это и означает сходимость метода. При этом [math]A^to Lambda= operatorname(lambda_1,ldots,lambda_n)[/math] .

Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]<vec,vec>[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]varphicolon[/math]

Таким образом, для компонент [math]vec,’,, vec,'[/math] будем иметь [math]bigl(vec,’,vec,’bigr)= bigl(vec,vecbigr)cdot! begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отсюда следует, что в двумерном пространстве матрица вращения имеет вид [math]H= begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отметим, что при [math]n=2[/math] для решения задачи требуется одна итерация.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Алгоритм метода вращений

1. Положить [math]k=0,

A^=A[/math] и задать 0″>[math]varepsilon>0[/math] .

2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^[/math] максимальный по модулю элемент [math]a_^,

Если [math]|a_^|leqslant varepsilon[/math] для всех [math]ine j[/math] , процесс завершить. Собственные значения определяются по формуле [math]lambda_i(A^)=a_^,

Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:

Если varepsilon»>[math]bigl|a_^bigr|>varepsilon[/math] , процесс продолжается.

3. Найти угол поворота по формуле [math]varphi^= frac operatorname frac<2a_^><a_^-a_^>[/math] .

4. Составить матрицу вращения [math]H^[/math] .

5. Вычислить очередное приближение [math]A^= bigl(H^bigr)^T A^ H^[/math] .Положить [math]k=k+1[/math] и перейти к пункту 2.

1. Используя обозначение [math]overline

_k= frac<2a_^><a_^-a_^>[/math] , можно в пункте 3 алгоритма вычислять элементы матрицы вращения по формулам

2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.

3. При [math]n=2[/math] для решения задачи требуется одна итерация.

Пример 2.5. Для матрицы [math]A=begin 2&1\1&3 end[/math] методом вращений найти собственные значения и собственные векторы.

1. Положим [math]k=0,

2°. Выше главной диагонали имеется только один элемент [math]a_=a_=1[/math] .

3°. Находим угол поворота матрицы по формуле (2.7), используя в расчетах 11 цифр после запятой в соответствии с заданной точностью:

4°. Сформируем матрицу вращения:

5°. Выполним первую итерацию:

Очевидно, след матрицы с заданной точностью сохраняется, т.е. [math]sum_^a_^= sum_^a_^=5[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.

2. Максимальный по модулю наддиагональный элемент [math]|a_|= 4,!04620781325cdot10^ . Для решения задачи (подчеркнем, что [math]n=2[/math] ) с принятой точностью потребовалась одна итерация, полученную матрицу можно считать диагональной. Найдены следующие собственные значения и собственные векторы:

Пример 2.6. Найти собственные значения и собственные векторы матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] .

1. Положим [math]k=0,

2°. Выделим максимальный по модулю элемент в наддиагональнои части: [math]a_^=2[/math] . Так как varepsilon=0,!001″>[math]a_=2> varepsilon=0,!001[/math] , то процесс продолжается.

3°. Находим угол поворота:

4°. Сформируем матрицу вращения: [math]H^= begin0,!85065&0&-0,!52573\ 0&1&0\ 0,!52573&0&0,!85065 end[/math] .

5°. Выполним первую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!236&1,!376&2,!33cdot10^\ 1,!376&4&0,!325\ 2,!33cdot10^&0,!325&1,!764 end[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.

2(1). Максимальный по модулю наддиагональный элемент [math]a_^=1,!376[/math] . Так как varepsilon=0,!001″>[math]a_^> varepsilon=0,!001[/math] , процесс продолжается.

3(1). Найдем угол поворота:

4(1). Сформируем матрицу вращения: [math]H^= begin 0,!902937&-0,!429770&0\ 0,!429770&0,!902937&0\ 0&0&1 end[/math] .

5(1). Выполним вторую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!891& 2,!238cdot10^&0,!14\ 2,!238cdot10^& 3,!345&0,!293\ 0,!14&0,!293&1,!764 end[/math] . Положим [math]k=2[/math] и перейдем к пункту 2.

2(2). Максимальный по модулю наддиагональный элемент varepsilon=0,!001″>[math]a_^=0,!293> varepsilon=0,!001[/math] .

3(2). Найдем угол поворота:

4(2). Сформируем матрицу вращения [math]H^= begin1&0&0\ 0&0,!9842924& -0,!1765460\ 0& 0,!1765460& 0,!9842924end[/math] .

5(2). Выполним третью итерацию и положим [math]k=3[/math] и перейдем к пункту 2:

2(3). Максимальный по модулю наддиагональный элемент varepsilon»>[math]a_^= 0,!138>varepsilon[/math] .

3(3). Найдем угол поворота:

4(3). Сформируем матрицу вращения: [math]H^= begin 0,!999646&0&-0,!026611\ 0&1&0\ 0,!026611&0&0,!999646 end[/math] .

5(3). Выполним четвертую итерацию и положим [math]k=4[/math] и перейдем к пункту 2:

2(4). Так как varepsilon»>[math]a_^=0,!025>varepsilon[/math] , процесс повторяется

3(4). Найдем угол поворота

4(4). Сформируем матрицу вращения: [math]H^= begin 0,!9999744&-0,!0071483&0\ 0,!0071483&0,!9999744&0\ 0&0&1 end[/math] .

5(4). Выполним пятую итерацию и положим [math]k=5[/math] и перейдем к пункту 2:

2(5). Так как наибольший по модулю наддиагональный элемент удовлетворяет условию [math]bigl|-6,!649cdot10^bigr| , процесс завершается.

Собственные значения: [math]lambda_1cong a_^= 6,!895,,

lambda_3cong a_^=1,!707,,[/math] . Для нахождения собственных векторов вычислим

X^3=begin-0,!473\-0,!171\0,!864 end[/math] или после нормировки

Видео:Собственные значения и собственные векторыСкачать

Собственные векторы – это в точности векторы фундаментальной системы решений

Собственно, на протяжении всего урока мы только и занимались тем, что находили векторы фундаментальной системы. Просто до поры до времени данный термин особо не требовался. Кстати, те ловкие студенты, которые в маскхалатах проскочили тему однородных уравнений, будут вынуждены вкурить её сейчас.

Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

Единственное действие состояло в удалении лишних строк. В результате получена матрица «один на три» с формальной «ступенькой» посередине.
– базисная переменная, – свободные переменные. Свободных переменных две, следовательно, векторов фундаментальной системы тоже два.

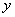
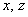
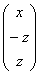
Выразим базисную переменную через свободные переменные: 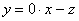. Нулевой множитель перед «иксом» позволяет принимать ему совершенно любые значения (что хорошо видно и из системы уравнений).

В контексте данной задачи общее решение удобнее записать не в строку, а в столбец:

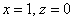
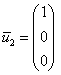
Паре соответствует собственный вектор:
Паре соответствует собственный вектор:

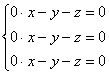
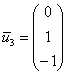
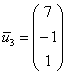
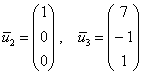
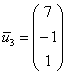
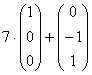
Примечание: искушенные читатели могут подобрать данные векторы и устно – просто анализируя систему , но тут нужны некоторые знания: переменных – три, ранг матрицы системы – единица, значит, фундаментальная система решений состоит из 3 – 1 = 2 векторов. Впрочем, найдённые векторы отлично просматриваются и без этих знаний чисто на интуитивном уровне. При этом даже «красивее» запишется третий вектор: . Однако предостерегаю, в другом примере простого подбора может и не оказаться, именно поэтому оговорка предназначена для опытных людей. Кроме того, а почему бы не взять в качестве третьего вектора, скажем, ? Ведь его координаты тоже удовлетворяют каждому уравнение системы, и векторы линейно независимы. Такой вариант, в принципе, годен, но «кривоват», поскольку «другой» вектор представляет собой линейную комбинацию векторов фундаментальной системы.

Ответ: собственные числа: 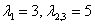, собственные векторы:

Аналогичный пример для самостоятельного решения:

Найти собственные числа и собственные векторы

Примерный образец чистового оформления в конце урока.

Следует отметить, что и в 6-ом и в 7-ом примере получается тройка линейно независимых векторов, поэтому исходная матрица представима в каноническом виде 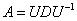. Но такая малина бывает далеко не во всех случаях:

Найти собственные числа и собственные векторы матрицы

Решение: составим и решим характеристическое уравнение:

Определитель раскроем по первому столбцу:

Дальнейшие упрощения проводим согласно рассмотренной методике, избегая многочлена 3-ей степени:

– собственные значения.

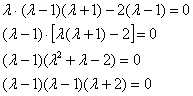
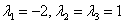
Найдем собственные векторы:

1) С корнем 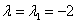затруднений не возникает:

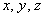
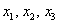
Не удивляйтесь, помимо комплекта в ходу также переменные – разницы тут никакой.

Из 3-го уравнения выразим 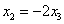– подставим в 1-ое и 2-ое уравнения:

Из обоих уравнений следует:

Пусть 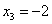, тогда:

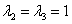
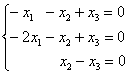
2-3) Для кратных значений получаем систему .

Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

(1) Ко второй строке прибавили первую строку, умноженную на –2.

(2) Последние две строки одинаковы, одну из них удалили.

(3) Дальше пошла уместная доводка матрицы методом Жордано-Гаусса: к первой строке прибавили вторую строку.

(4) У первой строки сменили знак.

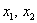
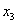
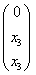
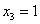
Переменные – базисные, переменная – свободная. Так как свободная переменная одна, то фундаментальная система решений состоит из одного вектора. И мы счастливые наблюдатели случая, когда кратным собственным числам соответствует единственный собственный вектор. Записываем в столбец общее решение системы: , и, задавая свободной переменной значение , получаем нашего героя:

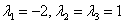
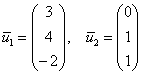
Ответ: собственные числа: , собственные векторы: .

Исходную матрицу нельзя представить в базисе из собственных векторов 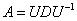по той простой причине, что такого базиса не существует – хоть трёхмерные векторы-столбцы и линейно независимы, но самих-то их всего лишь два. Недобор.

Шестое чувство мне подсказывает, что многие воодушевились на задание повышенной сложности:

Найти собственные числа и собственные значения матрицы

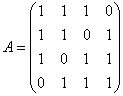
Можно ли записать данную матрицу в канонической форме?

Не беда, если дело застопорилось, в психотерапевтических целях отложите тетрадь с решением на чёрный день. Когда заест скука – самое то =)

Решения и ответы:

Пример 2: Решение: Найдем собственные значения. Составим и решим характеристическое уравнение:

– собственные значения.
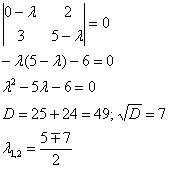
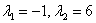
Найдем собственные векторы:
1)

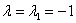
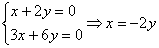
Пусть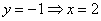
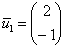
– собственный вектор.
2)

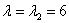
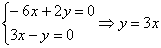
Пусть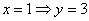
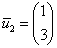
– собственный вектор.
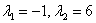
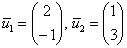
Ответ: собственные значения: , собственные векторы: .

Пример 5: Решение: сначала найдем собственные числа. Составим и решим характеристическое уравнение:

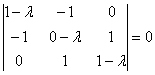
Определитель раскроем по первой строке:

– собственные значения.
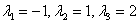
Найдем собственные векторы:
1)

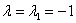
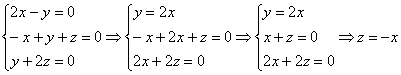
Пусть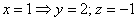

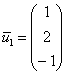
2)

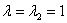
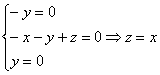
Пусть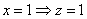

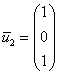
3)

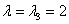
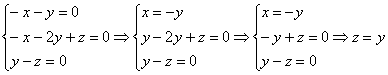
Пусть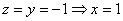

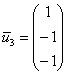
Ответ: собственные векторы:

Пример 7: Решение: составим и решим характеристическое уравнение:

– собственные значения.
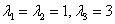
Найдем собственные векторы:
1-2)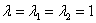

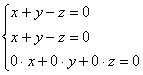
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

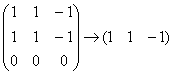
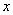
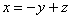
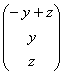
Выразим базисную переменную через свободные переменные: и запишем общее решение: . Найдём векторы фундаментальной системы, которые в данной задаче являются собственными векторами матрицы:
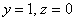
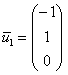
Паре соответствует собственный вектор:
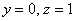
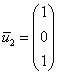
Паре соответствует собственный вектор:
Примечание: в качестве решения системы линейных уравнений данного пункта напрашивается тройка 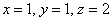, но столбец линейно выражается через векторы фундаментальной системы. Использование такого и подобных ему решений в качестве одного из собственных векторов корректно, но нестандартно.
3)

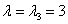
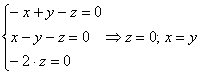
Пусть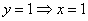

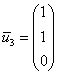
Ответ: собственные числа: 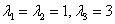, собственные векторы:

Пример 9: Решение: Составим и решим характеристическое уравнение:

Определитель вычислим понижением порядка. К третьей строке прибавим вторую строку, умноженную на –1. К четвёртой строке прибавим вторую строку, умноженную на :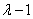

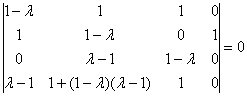
Разложим определитель по 4-му столбцу:

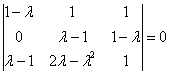
К третьей строке прибавим первую строку:

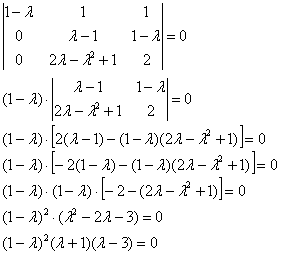
Собственные значения:

Найдем собственные векторы:
1)

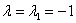
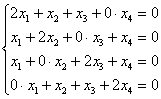
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

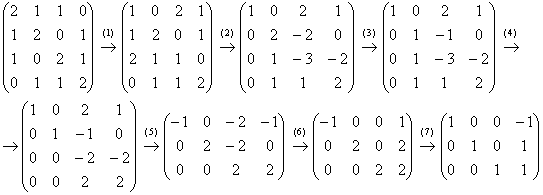
(1) Первую и третью строку поменяли местами.
(2) Ко 2-ой и 3-ей строкам прибавили первую строку, умноженную на –1 и –2 соответственно.
(3) Вторую строку разделили на 2.
(4) К 3-ей и 4-ой строкам прибавили вторую строку, умноженную на –1.
(5) Последние две строки пропорциональны, третью строку удалили. У первой строки сменили знак, вторую строку умножили на 2.
(6) К первой и второй строкам прибавили третью строку.
(7) У первой строки сменили знак, последние две строки разделили на 2.
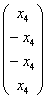
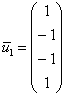
Выразив базисные переменные через свободную, запишем общее решение: . Придаём свободной переменной значение и получаем собственный вектор
2-3)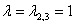

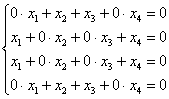
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

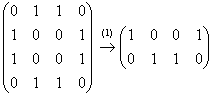
(1) Первая и четвёртая строки одинаковы. Вторая и третья строки одинаковы. Первую и вторую строку удалили из матрицы.
Выразим базисные переменные через свободные переменные :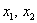

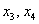
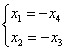
Таким образом, общее решение: .
Фундаментальная система состоит из двух векторов:
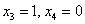
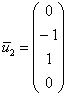
при получаем ;
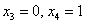
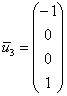
при получаем .

4)

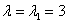
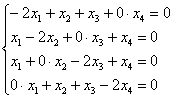
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

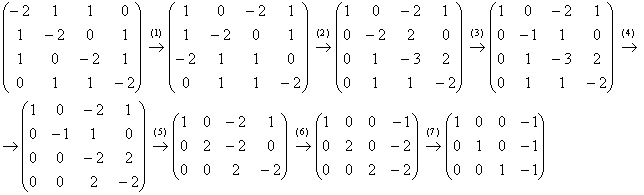
(1) Первую и третью строку поменяли местами.
(2) Ко 2-ой и 3-ей строкам прибавили первую строку, умноженную на –1 и 2 соответственно.
(3) Вторую строку разделили на 2.
(4) К 3-ей и 4-ой строкам прибавили вторую строку.
(5) Последние две строки пропорциональны, третью строку удалили. Вторую строку умножили на –2.
(6) К первой и второй строкам прибавили третью строку.
(7) Последние две строки разделили на 2.
Общее решение: . Придаём свободной переменной значение и получаем собственный вектор .

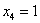
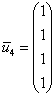
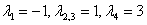
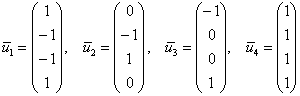
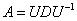
Ответ: собственные значения: , собственные векторы:
. Перечисленные четыре четырехмерных вектора линейно независимы, поэтому матрицу можно записать в канонической форме . Но лучше не надо =)

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Комплексные числа для чайников

Не занимайтесь комплексными числами после комплексного обеда

На данном уроке мы познакомимся с понятием комплексного числа, рассмотрим алгебраическую, тригонометрическую и показательную форму комплексного числа. А также научимся выполнять действия с комплексными числами: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня.

Не беспокойтесь, я вас напугал, я вас и рассмешу. Для освоения комплексных чисел не требуется каких-то специальных знаний из курса высшей математики, и материал доступен даже школьнику. Достаточно уметь выполнять основные алгебраические действия с «обычными» числами и немного рубить в тригонометрии. Впрочем, если что позабылось,
я напомню.

Урок состоит из следующих параграфов:
1) Понятие комплексного числа.
2) Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел.
3) Тригонометрическая и показательная форма комплексного числа.
4) Возведение комплексных чисел в степень.
5) Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.

На любой вкус и цвет – кому, что интересно. А комплексные числа действительно становятся наиболее интересной темой, после того, как студенты знакомятся с другими разделами высшей алгебры =). Если Вы являетесь чайником, или только-только приступили к изучению комплексных чисел, то параграфы лучше прочитать по порядку, без «перескоков».

Сначала вспомним «обычные» школьные числа. В математике они называются множеством действительных чисел и обозначаются буквой 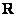(в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой). Все действительные числа сидят на знакомой числовой прямой:

Компания действительных чисел очень пёстрая – здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.

Видео:Как разложить вектор по базису - bezbotvyСкачать

Основные понятия о собственных значениях матриц

Большое число научно-технических задач, а также некоторые исследования в области вычислительной математики требуют нахождения собственных значений и собственных векторов матриц. Введем некоторые определения, необходимые для изложения материала данного раздела.

Рассмотрим, квадратную матрицу n-го порядка

(3.1)

Вектор x = <x1, x2,…,xn> называется собственным векторомматрицы А, соответствующим собственному значениюλ, если он удовлетворяет системе уравнений

Поскольку при умножении собственного вектора на скаляр он остается собственным вектором той же матрицы, его можно нормировать. В частности, каждую координату собственного вектора можно разделить на максимальную из них или на длину вектора; в последнем случае получится единичный собственный вектор.

Характеристической матрицейСданной матрицы Аназывается матрица вида

(3.3)

где Е — единичная матрица. Легко видеть, что систему (3.2) можно записать в виде

Если перейти к координатной форме записи вектора х, то с учетом (3.1) систему (3.4) можно записать в виде

(3.5)

Система (3.4) или (3.5) является однородной системой п линейных уравнений с п неизвестными. Она имеет ненулевые решения лишь тогда, когда ее определитель равен нулю: det C=0, причем решение не единственно.

Определитель характеристическойматрицы С является характеристический многочлен n-й степени относительно λ:

(3.6)

Корни этого многочлена являются собственными значениями матрицы А.

Для нахождения собственных векторов матрицы требуется решить систему линейных алгебраических уравнений, решение которой не единственно. Из линейной алгебры известно, что в этом случае структура общего решения системы имеет следующий вид: одно или несколько неизвестных, называемых свободными, могут принимать любые значения, а остальные неизвестные выражаются через свободные. Число свободных неизвестных равно числу уравнений системы, являющихся следствием остальных уравнений. На практике, если свободное неизвестное одно (что часто и бывает), его полагают равным некоторому числу, например единице. После этого остальные неизвестные (компоненты вектора) находят однозначно из подсистемы линейно независимых уравнений, в которой отброшено уравнение, являющееся следствием остальных. Эта процедура не влияет на результат решения задачи, поскольку, как уже отмечалось, собственные векторы находят с точностью до постоянного множителя.

Пример. Вычислить собственные числа и собственные векторы матрицы

Решение. Составим характеристический многочлен

Найдем корни этого многочлена второй степени:

Чтобы найти собственные векторы x1, х2, соответствующие собственным значениям λ1, λ2, составим системы уравнений типа (3.4), (3.5) для каждого из них.

При λ1 = 2 получим

или в координатной форме

Замечаем, что уравнения линейно зависимы. Поэтому оставляем лишь одно из них.

Из первого уравнения следует, что х2 = -х1.Неизвестное х1можно считать свободным, полагаем х1= 1. Тогда х2 = -1, и собственный вектор, соответствующий собственному значению λ1=2, имеет вид x1 = или x1= e1– е2, где е1, е2 – единичные орты выбранной базисной системы.

Аналогично находим второй собственный вектор, соответствующий собственному значению λ2 = 5. Опуская комментарии, получаем

Вектор x1 нормирован; нормируем также вектор х2, разделив его компоненты на наибольшую из них. Получим х2 = 0.5e1 + e2. Можно также привести векторы к единичной длине, разделив их компоненты на значения модулей векторов. В этом случае

Мы рассмотрели простейший пример вычисления собственных значений и собственных векторов для матрицы второго порядка. Нетрудно также провести подобное решение задачи для матрицы третьего порядка и для некоторых весьма специальных случаев.

В общем случае, особенно для матриц высокого порядка, задача о нахождении их собственных значений и собственных векторов, называемая полной проблемой собственных значений, значительно более сложная.

На первый взгляд может показаться, что вопрос сводится к вычислению корней многочлена (3.6). Однако здесь задача осложнена тем, что среди собственных значений часто встречаются кратные. И, кроме того, для произвольной матрицы непросто вычислить сами коэффициенты характеристического многочлена.

Отметим некоторые свойства собственных значений для частных типов исходной матрицы.

1. Все собственные значения симметрической матрицы действительны.

2. Если собственные значения матрицы действительны и различны, то соответствующие им собственные векторы ортогональны и образуют базис рассматриваемого пространства. Следовательно, любой вектор в данном пространстве можно выразить через совокупность линейно независимых собственных векторов.

3. Если две матрицы А и В подобны, т.е. они связаны соотношением

(3.7)

то их собственные значения совпадают (здесь Р – некоторая матрица). Преобразованиеподобия (3.7) можно использовать для упрощения исходной матрицы, а задачу о вычислении ее собственных значений свести к аналогичной задаче для более простой матрицы. Очевидно, самым лучшим упрощением матрицы (3.1) было бы приведение ее к треугольному виду

Тогда матрица (3.3) также имела бы треугольный вид. Как известно, определитель треугольной матрицы равен произведению ее диагональных элементов, поэтому характеристический многочлен (3.6) в этом случае имеет вид

Собственные значения матрицы, равные корням этого многочлена, можно получить сразу:

Таким образом, собственные значения треугольной матрицы равны ее диагональным элементам. То же самое, естественно, относится и к диагональной матрице, которая является частным случаем треугольной.

Некоторые типы матриц удается привести к треугольному виду с помощью преобразования подобия. В частности, симметрическую матрицу можно привести к диагональному виду. На практике часто используется приведение симметрической матрицы к трехдиагональному виду. Процедура вычисления собственных значений для полученной матрицы значи­тельно упрощается по сравнению с задачей для исходной матрицы.

Существует ряд методов, основанных на использовании преобразования подобия, позволяющего привести исходную матрицу к более простой структуре. Мы рассмотрим ниже один из них – метод вращений.

🎥 Видео

Собственные векторы и собственные значенияСкачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

7 4 Собственные векторы и собственные значенияСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Матричный метод решения систем уравненийСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать