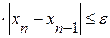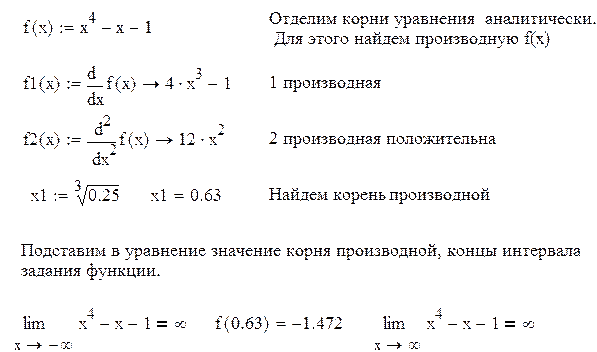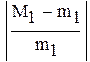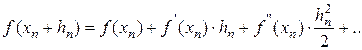| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Кафедра прикладной математики и вычислительной техники
Решение нелинейных уравнений в Excel и Mathcad
к выполнению лабораторных работ
по дисциплине «Вычислительная математика»
Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , — Самара: СГАСУ, 20с.
Методические указания разработаны в соответствии с Государственным образовательным стандартом изучения дисциплины «Вычислительная математика».
Рассмотрена реализация численных методов при решении нелинейных уравнений и систем уравнений в Excel и MathCad. Приведены варианты заданий для индивидуального выполнения и вопросы для самоконтроля и тестирования.
Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения.
Рецензент к. ф-м. н.
Ó , составление, 2012
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
1.2 Отделение корней
1.3 Уточнение корней стандартными средствами Excel и Mathcad
1.4 Метод деления отрезка пополам
1.6 Метод Ньютона (касательных)
1.7 Комбинированный метод
1.8 Метод итераций
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
2.2 Решение систем нелинейных уравнений методом Ньютона
2.3 Решение систем нелинейных уравнений методами итераций
3 Задания к лабораторным работам
Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения
Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения
Лабораторная № 3. Решение систем нелинейных уравнений
Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем
4 Вопросы и тесты для самоконтроля
Список рекомендуемой литературы
- 1 Решение нелинейного уравнения
- 1.1 Общие сведения о решении нелинейного уравнения
- 1.2 Отделение корней
- 1.3 Уточнение корней стандартными средствами Excel и Mathcad
- 1.4 Метод деления отрезка пополам
- 1.5 Метод хорд
- 1.6 Метод Ньютона (касательных)
- 2 Решение систем нелинейных уравнений
- 2.1 Общие сведения о решении систем нелинейных уравнений
- 2.2 Решение систем нелинейных уравнений методом Ньютона
- 2.3 Решение систем нелинейных уравнений методами итераций
- Метод половинного деления (метод дихотонии) в MathCAD.
- Метод хорд в маткаде
- Методы решения нелинейных уравнений в MathCAD
- Численные методы решения нелинейных уравнений. Метод хорд.
- 📺 Видео
Видео:14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

1 Решение нелинейного уравнения
Видео:Метод половинного деления решение нелинейного уравненияСкачать

1.1 Общие сведения о решении нелинейного уравнения
Как правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн.
В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т. е. находят его значение с требуемой точностью.
Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т. е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т. е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс).
Видео:7 Метод половинного деления Mathcad Численные методы решения нелинейного уравненияСкачать

1.2 Отделение корней
Отделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0.
Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной.
Пример Найти с точностью до целых все корни нелинейного уравнения y(x)=x3 ‑ 10x + 7=0 а) построив таблицу и б) построив график. Найти корень уравнения на выделенном отрезке, используя опции «Подбор параметра» и «Поиск решения».
Решение Создадим в Excel таблицу, содержащую аргументы и значения функции и по ней построим точечную диаграмму. На рисунке 1 приведен снимок решения.
На графике видно, что уравнение имеет три корня, принадлежащие отрезкам [-4, -3], [0, 1] и [2, 3]. Эти отрезки можно выявить и наблюдая за сменой знаков функции в таблице. По построенному графику можно сделать вывод, что на указанных отрезках функция f(x) монотонна и, следовательно, на каждом из них содержится только по одному корню.
Такой же анализ может быть выполнен и в пакете Mathcad. Для этого достаточно набрать определение функции f(x), используя оператор присваивания (:=) и естественные общепринятые обозначения математических операций и стандартных функций, задать цикл для изменения аргумента, например, а затем вывести на экран таблицу значений функции (расположенными в одной строке командами x= f(x)=) и график. Цикл можно задать, например, командой x:=-5,-4.5…5. Шаг цикла формируется путем задания начального и следующего за ним значений переменной, а перед конечным значением переменной ставится точка с запятой, которая будет визуально отображена на экране в виде многоточия.
Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения
Видео:Метод половинного деленияСкачать

1.3 Уточнение корней стандартными средствами Excel и Mathcad
Во всех методах уточнения корней необходимо задать начальное приближение, которое затем и будет уточняться. Если уравнение имеет несколько корней, в зависимости от выбранного начального приближения будет найден один из них. При неудачно выбранном начальном приближении решение может и не быть найдено. Если в результате первого этапа расчетов уже выделен отрезок, содержащий единственный корень уравнения, в качестве начального приближения можно взять любую точку этого отрезка.
В Excel для уточнения значений корней можно использовать опции «Подбор параметра» и «Поиск решения». Пример оформления решения приведен на рисунках 2 и 3.
Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel
Рисунок 3 – Результаты использования средств решения уравнения в Excel
В Mathcad для уточнения корней уравнения можно использовать функцию root(….) или блок решения. Пример использования функции root(…) приведен на рисунке 4, а блока решения на рисунке 5. Следует обратить внимание, что в блоке решения (после заголовка блока Given) между левой и правой частями уравнения должен стоять жирный знак равенства (тождества), который можно получить выбором из соответствующей палитры инструментов, либо нажатием одновременно клавиши Ctrl и =.

Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad
Как видим, каждый стандартный инструмент находит решение уравнения с определенной точностью. Эта точность зависит от метода, используемого в пакете и, в определенной степени, настроек пакета. Управлять точностью результата здесь достаточно сложно, а часто и невозможно.
В то же время, очень просто построить собственную таблицу или написать программу, реализующие один из методов уточнения корней. Здесь можно использовать критерии точности расчета, задаваемые пользователем. При этом достигается и понимание процесса расчетов без опоры на принцип Митрофанушки: «Извозчик есть, довезет».
Далее рассмотрены несколько наиболее распространенных методов. Отметим очевидный момент: при прочих равных условиях тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден с меньшим числом вычислений функции f(x) (при этом достигается и максимальная точность при одинаковом числе вычислений функции).
Видео:12й класс; Информатика; "Численные методы. Метод половинного деления"Скачать

1.4 Метод деления отрезка пополам
В этом методе на каждом шаге отрезок делится на две равные части. Затем сравнивают знаки функции на концах каждой из двух половинок (например, по знаку произведения значений функций на концах), определяют ту из них, в которой содержится решение (знаки функции на концах должны быть разные), и. сужают отрезок, перенося в найденную точку его границу (а или b). Условием окончания служит малость отрезка, где содержится корень («точность по x»), либо близость к 0 значения функции в средине отрезка («точность по y»). Решением уравнения считают середину отрезка, найденного на последнем шаге.
Пример. Построить таблицу для уточнения корня уравнения x3 –10x+7=0 на отрезке [-4, -3] методом деления отрезка пополам. Определить сколько шагов надо сделать методом деления отрезка пополам и какая при этом достигается точность по х, для достижения точности по y, равной 0,1; 0,01; 0, 001.
Решение Для решения можно использовать табличный процессор Excel, позволяющий автоматически продолжать строки. На первом шаге заносим в таблицу значения левого и правого концов выбранного начального отрезка и вычисляем значение середины отрезка с=(a+b)/2, а затем вводим формулу для вычисления функции в точке a (f(a)) и растягиваем (копируем) её для вычисления f(c) и f(b). В последнем столбца вычисляем выражение (b—a)/2, характеризующего степень точности вычислений. Все набранные формулы можно скопировать во вторую строку таблицы.
На втором шаге нужно автоматизировать процесс поиска той половины отрезка, где содержится корень. Для этого испльзуется логическая функция ЕСЛИ (Меню: Вставка

Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк.
Итерационный процесс завершается, когда очередное значение в последнем столбце становится меньшим, чем заданный показатель точности ex. При этом, значение середины отрезка в последнем приближении, принимается в качестве приближенного значения искомого корня нелинейного уравнения. На рисунке 6 приведен снимок решения. Для построения аналогичного процесса в Mathcad можно использовать бланк, подобный приведенному на рисунке 7. Число шагов N может варьироваться до достижения в таблице результатов требуемой точности. При этом таблица будет автоматически удлиняться или укорачиваться.
Итак, одним из трех корней нелинейного уравнения x3 – 10x + 7=0, найденным с точностью e=0,0001, является x= — 3,46686. Как мы видим, он действительно принадлежит отрезку [-4; -3].
Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel
Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad
Видео:1.1 Решение нелинейных уравнений метод деления отрезка пополам (бисекций) Мathcad15Скачать

1.5 Метод хорд
В этом методе нелинейная функция f(x) на отделенном интервале [а, b] заменяется линейной – уравнением хорды, т. е. прямой соединяющей граничные точки графика на отрезке. Условие применимости метода – монотонность функции на начальном отрезке, обеспечивающая единственность корня на этом отрезке. Расчет по методу хорд аналогичен расчету методом деления отрезка пополам, но теперь на каждом шаге новая точка x внутри отрезка [a,b] рассчитывается по любой из следующих формул:

Видео:Решение нелинейного уравнения методом половинного деления (программа)Скачать

1.6 Метод Ньютона (касательных)
Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только на каждом шаге кривая f(x) заменяется касательной к ней, проведенной в предыдущей найденной точке. В качестве начальной точки в зависимости от свойств функции берется или левая граница отрезка, содержащего корень – x0 = а (если f(а) f»(х) > 0), или правая его граница: x0 = b (если f(b) f»(х)>0). Расчет нового приближения на следующем шаге i+1 производится по формуле:

Алгоритм применим для монотонных функций, сохраняющих выпуклость или вогнутость в промежутке между начальным приближением и корнем уравнения (т. е. должен сохраняться знак первой и второй производных функции f(x)). работоспособен при выпуклых и монотонных функциях f(x). В расчетах нет необходимости отслеживать две границы отрезка, поэтому достаточно на каждом шаге вычислять значения x, f(x) и f′(x). При этом легко оценить «точность по y», по значению левой части уравнения на очередном шаге. Для оценки «точности по x» нужно отслеживать разницу приближений на предыдущем и последующих шагах, которая связана с разницей между найденным приближением и точным значением корня.
Следует обратить внимание на следующую особенность метода: последовательность x1, x2, x3,… приближается к корню с другой стороны, в отличие от использования метода хорд при прочих равных условиях.
Главным достоинством метода касательных является квадратичная скорость сходимости, что во многих случаях может привести к сокращению числа вычислений функции.
Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001.
Точность вычислений можно оценить из соотношения
Видео:Метод половинного деления. ДихотомияСкачать

2 Решение систем нелинейных уравнений
Видео:Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

2.1 Общие сведения о решении систем нелинейных уравнений
Систему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:
где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные.
Как и в случае систем линейных уравнений, решением системы является такой вектор X*, который при подстановке обращает одновременно все уравнения системы в тождества.
Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно.
Численные методы решения системы уравнений носят итерационный характер и требуют задания начального приближения X0.
Рассмотрим две группы таких методов: метод Ньютона с различными его модификациями и методы итераций (простых итераций и Зейделя).
Видео:8 Метод половинного деления Calc Excel Численные методы решения нелинейного уравненияСкачать

2.2 Решение систем нелинейных уравнений методом Ньютона
Будем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:
Начальные значения x0 и y0 определяются графически. Для нахождения каждого последующего приближения (xi+1, yi+1) используют вектор значений функций и матрицу значений их первых производных, рассчитанные в предыдущей точке (xi, yi).

Для расчета новых приближений на шаге i+1 используется матричная формула

Следует обратить внимание, что в последней формуле используется вычисление матрицы, обратной к матрице первых производных.
Расчет останавливают при выполнении одного (а иногда и обоих) из двух условий. Первое из них заключается в том, что на очередном шаге максимальное по модулю из изменений аргументов x и y становится меньше заданная погрешность по аргументам. В соответствии со вторым из условий, на очередном шаге максимальное по модулю значение левых частей уравнений должно отличаться от нуля меньше, чем заданная погрешность по функциям.
В упрощенном методе Ньютона матрица производных и матрица, обратная к ней вычисляются только один раз (в начальной точке) и для расчетов используется матричная формула

Приведенные формулы особенно легко записать в Mathcad, где имеются операторы для вычисления производных и действий с матрицами. Однако при правильном использовании матричных операций эти формулы достаточно просто записываются и в Excel. Правда, здесь придется заранее получить формулы для вычисления производных. Для аналитического вычисления производных также может быть использован Mathcad.
Видео:Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

2.3 Решение систем нелинейных уравнений методами итераций
Для реализации этих методов исходную систему уравнений необходимо путем алгебраических преобразований явно выразить каждую переменную через остальные. Для случая двух уравнений с двумя неизвестными новая система будет иметь вид

Для решения такой системы задаются начальным приближением x0, y0. Уточненные решения получают по шагам, подставляя в правые части уравнений значения, найденные на предыдущем шаге. В методе простых итераций для уточнения решения используют формулы:

Если одно из решений системы и начальные значения x0 и y0 лежат в области D, задаваемой неравенствами: a ≤ x ≤ b, c ≤ y ≤ d, то расчет по методу простых итераций сходится при выполнении в области D соотношений:
Видео:Метод половинного деления - ВизуализацияСкачать

Метод половинного деления (метод дихотонии) в MathCAD.


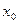



Делим отрезок 
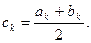

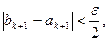

Преимущество данного метода: данный метод всегда сходится к решению, если правильно установлен 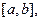
Недостаток: численное решение по методу дихотомии требует достаточно большого времени, по сравнению с другими методами. Устойчивость численного решения означает, что алгоритм всегда приводит к решению. Следовательно, метод дихотомии является устойчивым.
Метод Ньютона в MathCAD.






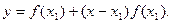

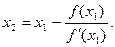






Недостатком метода Ньютона является то, что ни при любом начальном приближении 



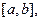

Для организации итерационных вычислений в MathCAD используется функция
Формат: 
Метод простых итераций в MathCAD.
Пусть задана некоторая нелинейная функция 












Графические возможности пакетов символьных вычислений: работа с двумерной и трехмерной графикой в MathCAD, Mathematica, Maple; построение графиков функций в различных системах координат.
MathCAD.
Графические области делятся на три основных типа — двумерные графики, трехмерные графики и импортированные графические образы. Двумерные и трехмерные графики строятся caмим MathCAD на основании обработанных данных.
Для создания декартового графика: Установить маркер в пустом месте рабочего документа. Выбрать команду Insert => Graph => Х-У Plot, или нажать комбинацию клавиш Shift + @, или щелкнуть кнопку (изображение графика) на панели Graph. Ввести в средней метке под осью X 1ю независимую переменную, через запятую — 2ю и так до 10, например x1,x2, . 4. Ввести в средней метке слева от вертикальной оси Y 1ю зависимую переменную, через запятую — 2ю, например y1(х1),y2(х2). 5. Щелкнуть за пределами области графика, чтобы начать его построение. Если строятся графики нескольких функций в одном шаблоне, то функции следует разделять запятыми.
Форматирование двумерных графиков
Для вывода окна форматирования двумерного графика достаточно поместить указатель мыши в область графика и дважды щелкнуть левой кнопкой мыши. В окне документа появится окно форматирования. Оно имеет ряд вкладок:- Х-У Axes (Оси Х-У) — задание параметров форматирования осей;- Traces (Линии) — задание параметров форматирования линий графика;
— Labels (Метки) — задание параметров форматирования меток осей,- Default (по умолчанию) — назначение установленных параметров форматированияпараметрами по умолчанию
Форматирование осей графика
На вкладке Х-У Axes содержатся следующие основные параметры, относящиеся к осям X и У (Axis X и Axis У); LogScale — установление логарифмического масштаба; GridLines — установка линий масштабной сетки, Numbered -установка цифровых данных по осям; Autoscale — автоматическое масштабирование графика; ShowMarkers — установка делений по осям; AutoGrid — автоматическая установка масштабных линий; Number of Grids — установка заданного числа масштабных линий; Группа Axes Style позволяет задать стиль отображения координатных осей:Boxed -оси в виде прямоугольника; Crossed — оси в виде креста, None — отсутствие осей, Equal Scales — установка одинакового масштаба по осям графика.
Форматирование линий графиков
Эта вкладка служит для управления отображением линий, из которых строится график. На этой вкладке представлены следующие параметры: Legend Label — выбор типа линии в легенде; Symbol — выбор символа, который помещается на линию, для отметки базовых точек графика; Line– установка типа линии, Сolor — установка цвета линии и базовых точек, Type — установка типа графика, Weight — установка толщины линии.
Узловые точки (точки, для которых вычисляются координаты) графиков часто требуется выделить какой-нибудь фигурой. Список в столбце Линия позволяет выбрать типы линий: непрерывная, пунктирная, штрих — пунктирная.
Раскрывающийся список столбца Туре позволяет выбрать следующие типы линий графика: lines — построение линиями, points — построение точками, error — построение вертикальными черточками с оценкой интервала погрешностей, bar — построение в виде столбцов гистограммы, step — построение ступенчатой линией, draw — построение протяжкой от точки до точки.
Задание надписей на графиках
Эта вкладка позволяет вводить в график дополнительные надписи. Для установки надписей служат поля ввода: Title — установка титульной надписи к рисунку, Axes X — установка надписи по оси X, Axes Y — установка надписи по оси У.
В группе Заголовок имеются переключатели сверху и снизу для установки титульной надписи либо над графиком, либо под ним.
Параметры графиков по умолчанию
Вкладка «Default» позволяет назначить установленные на других вкладках параметры форматированияпараметрами по умолчанию.
В полярной системе координат каждая точка задается углом w и длиной его радиус-вектора R(W). График функции обычно строится при изменении угла W в определенных пределах, чаще всего от О до 2π. Выбор команды Polar Plot в подменю Graph меню Insert или нажатие комбинации клавиш Ctrl+7 выводит шаблон таких графиков. Этот шаблон имеет форму окружности и содержит места ввода данных. После вывода шаблона следует ввести W в место ввода снизу и функцию R (W) в место ввода слева, а также указать нижний предел изменения длины радиус-вектора R(W) — Rmin – в место ввода справа снизу и верхний предел –R max -в месте ввода справа сверху. Эти места ввода становятся видимыми при выделении графика.
Построение графиков поверхностей
Трехмерные, или ЗD-графики, отображают функции двух переменных вида Z(X, Y). Для построения трехмерного графика нужно:
1) определить функцию двух переменных х и у.2)Используя палитру графики, ввести шаблон трехмерного графика.3) на единственное место ввода под шаблоном ввести имя функции z. 4) вывести указатель мыши за пределы графика и щелкните левой кнопкой будет построен график в виде «проволочного каркаса.
Для изменения вида графиков трехмерных поверхностей используется их форматирование. При построении трехмерных графиков применяют функцию MathCAD CreateMesh — создает сетку на поверхности, определенной функцией F. x0,x1,y0,y1 — диапазон изменения переменных, xgrid, ygrid — размеры сетки переменных, fmap — функция отображения. Все параметры, за исключением F – факультативные. Функция Вид трехмерной фигуры зависит от того, под какими yглами относительно осей X, Y и Z ее рассматривают.
Для построения пересекающихся фигур на одном графике надо раздельно задать матрицы соответствующих поверхностей и после вывода шаблона 3D-графика перечислить эти матрицы под ним с использованием в качестве разделителя запятой.
Форматирование трехмерных графиков
Окно форматирования трехмерных графиков вызывается аналогично окну форматирования двумерных графиков и имеет ряд вкладок: General — установка общих параметров форматирования, Axes — установка параметров форматирования координатных осей, Appearance — установка вида графика, Lighting — задание условий освещения и выбор схемы освещения.
Mathematica.
Для построения двухмерных графиков ф-ций вида f(x) используется встроенная в ядро ф-ция Plot: Plot [f, ] — возвращает объект — график ф-ции f аргумента х в интервале от xmin до xmax; Plot [, ] — возвращает объект в виде графиков ряда ф-ций fi.
Важным средством настройки графиков являются графические директивы. Синтаксис их подобен синтаксису функций. Однако опции не возвращают объектов, а лишь влияют на их характеристики. Используются следующие директивы двухмерной графики: AbsoluteDashing [
- ] — задает построение последующих линией пунктиром со смежными (последовательными) сегментами, имеющими абсолютные длины dl, d2. (повторяемые циклически). Значения длины di задаются в пикселях; AbsolutePointSize [d] — задает построение последующих точек графика в виде кружков с диаметром d (в пикселях); AbsoluteThickness[d] — задает абсолютное значение толщины для последующих рисуемых линий (в пикселях), Dashing[] — задает построение последующих линий пунктиром с последовательными сегментами длиной rl, г2,… повторяемыми циклически, причем ri задается как дробная часть полной ширины графика.
PointSize[d] — задает вывод последующих точек графика в виде кружков с относительным диаметром d, заданным как дробная часть от общей ширины графика, Thickness[r] — устанавливает толщину г для всех последующих линий, заданную как дробная часть от полной ширины графика.
Применение графических директив совместно с опциями позволяет создавать графики самого различного вида.
При построении графиков часто требуется изменение их вида и тех или иных параметров и опций. В этом случае удобно использовать следующую функцию- директиву:
Show[plot] — построение графика,
Для построения примитивной двухмерной графики используется функция
Graphics[primitives, options] представляет двухмерное графическое изображение.
Возможно построение графиков в полярной системе координат двумя способами. Первый способ основан на использовании обычной Декартовой системы координат. Координаты каждой точки при этом задаются в параметрическом виде x=fx(t) и y=fy(t), где независимая переменная t меняется от минимального значения tmin до максимального tmax с шагом dt. Особенно удобно применение таких функций для построения замкнутых линий, таких как окружности, эллипсы, циклоиды и др.
Для построения параметрически заданных функции используются следующие графические средства: ParametricPlot[, ] — строит параметрический график с координатами fx и fу (соответствующими х и у ) получаемыми как функции от t;
Принципы построения поверхностей и ЗD-фигур/
Функция двух переменных z = f(x,y) в пространстве o6pазуетнекоторую поверхность или трехмерную фигуру. Для их построения приходится использовать координатную систему с тремя осями координат: х,у и z. Поскольку экран дисплея ПК плоский, то на самом деле объемность фигур лишь имитируется — используется хорошо известный способ наглядного представления 3D-фигур в виде аксонометрического графика.
Вместо построения всех точек фигуры обычно строится ее каркасная модель, содержащая линии разреза фигуры по взаимно перпендикулярным плоскостям. В результате фигура представляется в виде совокупности из множества криволинейных четырехугольников. Для придания фигуре большей естественности используются алгоритм удаления невидимых линий каркаса и функциональная закраска четырехугольников по правилу бокового освещения фигуры.
Для построения графиков поверхностей используется основная графическая функция
Plot3D[f, <х, xmin, xmax), ] — строит трехмерный график функции f переменных х и у.
Помимо опций для трехмерной графики используется ряд графических директив и функций.
Часто поверхность задается массивом своих высот (аппликат ). Для построения графика в этом случае используется графическая функция ListPlot3D.
Особый шик построениям ЗD-фигур и поверхностей придает функция ParametricPlot3D, в которой предусмотрено параметрическое задание всех трех функций, описывающих координаты каждой точки.
Эта функция имеет также множество опций. Параметрическое задание функций позволяет легко строить сложные пространственные фигуры, визуально весьма напоминающие реальные объекты.
Для построения графиков функций в полярной системе координат заданы следующие функции:
PolarPlot[f,] — строит график функции в полярной системе координат как положение конца радиус-вектора f при изменении угла от tmin до tmax;
Для построение графиков неявных функций –используется пакет ImplicitPlot.
Построение ЗD -параметрических графиков- ParametricPlot3D
Для построения трехмерных поверхностей в сферической и цилиндрической системах координат служат функции соответственно:
Maple.
Графика Maple V реализует все варианты математических графиков — от построения графиков простых функций в декартовой и в полярной системах координат до создания реалистических образов сложных пересекающихся в пространстве фигур с их функциональной окраской. Возможны наглядные графические иллюстрации решений самых разнообразии уравнений, включая системы дифференциальный уравнений.
В само ядро Maple V встроено ограниченное число функций графики. Это прежде всего функция для построения двумерных графиков (2D-типа) – plot и функция для построения трехмерных графиков (ЗD-типа) — plot3d. Они позволяют строить графики наиболее распространенных типов. Для построения графиков специального типа (например, в виде векторных полем градиентов, решения дифференциальных уравнений построения фазовых портретов и т.д.) в пакеты расширения системы Maple V включено большое число различных графических функций. Для их вызова необходимы соответствующие указания.
Для построения двумерных графиков служит функция plot. I Она задается в виде: plot(f, h, v) или plot(f, h, v, о), где f функция (или функции), чей (чьи) график(и) строятся, h — переменная с указанием области ee изменения по горизонтали, v — заданная опционально переменная с указанием области изменения по вертикали, о — опция или набор опций, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т.д.)
55. Назначение издательской системы TeX (LaTeX). Основные понятия пакета: исходный файл; спецсимволы; команды и их задание в тексте; структура исходного текста. Принципы работы с математическим текстом: форматирование текста; правила набора формул, нумерация и переносы в формулах; таблицы спецзнаков; набор матриц.
ТEX — это комп. программа, созданная Дональдом Кнутом. LATEX — макропакет, позволяющий авторам верстать и печатать их работы с высоким типографским качеством, при помощи заранее определенных, профессиональных макетов. LATEX был написан Leslie Lamport . В качестве механизма для верстки он использует TEX. Позже LATEX был обновлен и эту новую версию называют LATEX2e.
Исходными данными (файлом) для TEX являются обычный текстовый файл в ASCII. Его можно создать в любом текстовом редакторе. Он содержит текст документа вместе с командами, указывающими TEX, как верстать текст.
> символы, такие, как пробел или табуляция, трактуются TEX одинаково, как >. Пустая строка между двух строк текста определяет конец абзаца. Следующие символы (спецсимволы) являются зарезервированными символами, которые либо имеют в TEX специальное значение, либо имеются не во всех шрифтах. $ & % # _
^ . Например, знак $ используют для обозначения математической формулы, знак % для комментария внутри текста документа, фигурные скобки для записи имен окружений и т.д. Эти символы можно использовать в документах, добавляя к ним префикс >: Знак > нельзя вводить, добавляя перед ним еще один, так как эта команда (\) используется для разрыва строки.
Каждый входной файл должен начитаться с команды documentstyle Она указывает, документ какого типа вы собираетесь писать. После этого, вы можете включать команды, влияющие на стиль документа в целом, или загружать пакеты, добавляющие новые возможности в систему TEX. Для загрузки такого пакета используется команда
Когда вся настройка закончена, вы начинаете тело текста командой
В конце документа вы добавляете команду end
Минимальный файл TEX
documentstyle[12pt, russian, 0011]%report>%
input 000pream.tex %Преамбула
input 142-143.tex % Подключение файлов, содержащих текст документа
Я изучаю TeX % или непосредственное написание текста документа
Стили документов documentstyle[опции]
Здесь стиль определяет тип создаваемого документа. Таблица перечисляет классы документов.
article для статей в научных журналах, , приглашений. reportдля более длинных отчетов, содержащих несколько глав, bookдля настоящих книг
Специальные буквы и символы
Для набора кавычек в TEX используйте два знака ` в качестве открывающей кавычки и два знака ‘ в качестве закрывающей. TEX знает 4 вида тире. 3 из них вы можете получить различным числом последовательных знаков -. Четвертое — математический знак минус. Эти тире называются так: — дефис, — короткое тире, — длинное тире и $-$ знак минуса. Для многоточия есть специальная команда, называющаяся ldots или dots. Чтобы подчеркнуть текст, используется команда underline. Чтобы взять часть текста в рамку, используется команда fbox
Для получения ровного правого края вывода TEX вставляет различные интервалы между словами. В конце предложения он вставляет слегка больший интервал, делая текст более читабельным. TEX предполагает, что предложения заканчиваются точками, вопросительными или восклицательными знаками. Если точка следует за буквой в верхнем регистре, она не считается концом предложения, так как точки после букв верхнего регистра обычно используются для сокращений.
Любое исключение из этих предположений должно быть явно оговорено автором. Знак > перед пробелом дает в результате пробел, который не будет увеличен. Знак > дает пробел, который не может увеличиться и который, кроме того, запрещает разрыв строки. Команда @ перед точкой указывает, что эта точка заканчивает предложение, несмотря на то, что стоит за буквой верхнего регистра.
Для выделения шрифтом определенной части текста используется команда em. Если текущий шрифт прямой, то эта команда переключает шрифт на курсивный, а если имеет наклон, то на обычную гарнитуру roman.
| Команда — Название гарнитуры, bf — Полужирный шрифт, it – Курсив, sl — Наклонный шрифт, rm — Обычный шрифт |
Для верстки специальных видов текста LATEX определяет множество окружений для разных типов форматирования:
где название определяет окружение. Окружения можно вызывать внутри окружений, соблюдая порядок вызова и возврата: begin. begin. end. end
Окружение itemize подходит для простых списков, окружение enumerate — для нумерованных списков, а окружение description — для описаний.
Окружения flushleft и flushright форматируют абзацы, выровненные влево или вправо. Окружение center дает центрированный текст. Если вы не используете \ для указания разрывов строк, TEX определит их автоматически.
Для набора математических формул используются в качестве ограничителей знаки $, причем 1) если формула идет в тексте, то она ограничивается с обеих сторон одним знаком $, если же формула располагается на отдельной строке по центру (выключная), то она ограничивается двумя знаками доллара с каждой стороны.
Для того чтобы набрать формулу с номером, нужно воспользоваться командой:
В этом случае формулы будут нумероваться автоматически самим Tex.
Двухъярусная дробь верстается командой frac. Оператор интеграла печатает команда int, а команда oint -контурный интеграл. Верхние и нижние пределы указываются при помощи знаков > и >, так же, как верхние и нижние индексы. В некоторых случаях необходимо указать корректный размер математического ограничителя вручную, для этого есть команды big, Big, bigg и Bigg, служащие префиксами к большинству команд ограничителей. Все основные математические символы имеют определенные правила набора для их корректного изображения при трансляции. Для этого используются таблицы спецзнаков.
 |  |
 |
«Теоретические основы информатики»
Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Метод хорд в маткаде
БлогNot. Методы решения нелинейных уравнений в MathCAD
Методы решения нелинейных уравнений в MathCAD
Реализуем для некоторого уравнения 4 наиболее популярных численных метода для решения нелинейных уравнений. При этом мы стремимся именно запрограммировать методы, а не воспользоваться встроенным инструментом Given. Find или функциями root , polyroot . Об этих способах решения почитайте, например, здесь.
Определим функцию уравнения f(x)=0 как функцию пользователя, интервал поиска решения зададим переменными a и b . Найти этот интервал можно, например, табличным или графическим методом:
Начальный интервал [a,b] должен быть таким, чтобы значения f(a) и f(b) имели противоположные знаки. Если искомый корень уравнения окажется единственным на интервале, то совсем хорошо 🙂
Логика метода дихотомии (возможно, более правильные названия – метод бисекции, метод половинного деления) довольно проста: если на концах выбранного интервала [a,b] знаки функции совпадают (произведение f(a)*f(b)>0 ), то вернуть результат «недопустимый интервал» (вернём в этом случае ответ «бесконечность»), в противном случае до тех пор, пока длина интервала не станет меньше заданной погрешности ε , будем находить середину текущего интервала c=(a+b)/2 , считать в ней значение функции и проверять, какую из половин отрезка [a,c] или [c,b] нужно отбросить для выполнения следующего шага – а именно, ту, в которой знак f(c) совпадает со знаком функции на левой или правой границе интервала (в листинге – проверка f(a)*f(c)>0 ). Для большей точности вернём середину «последнего» интервала [a,b] , меньшего ε :
В методе простой итерации исходное уравнение f(x)=0 представляется в эквивалентном виде φ(x)=x (что, вообще говоря, можно сделать бесконечным числом способов), а затем шаг метода выполняется по формуле xk+1 = φ(xk) , пока не будет достигнута заданная точность |xk+1-xk| . Если выбрать φ(x)=x-c*f(x) , то константу c целесообразнее всего искать методом релаксации, для которого c=2/(M+m) , где M – максимальное из значений первой производной на концах отрезка или в находящихся на нём точках перегиба функции (точках, где f”(x)=0 ), а m – минимальное из таких значений. Вот соответствующий расчёт в MathCAD:
Если заданной сходимости нет в течение 10000 шагов, в подпрограмме предусмотрен аварийный выход.
Численный метод Ньютона решения нелинейного уравнения основан на формуле вида xk+1 = xk-f(xk)/f'(xk) , обеспечивающей наилучшую сходимость, но требующей дополнительного вычисления производной на каждом шаге. Так как производные для MathCAD – не проблема, можно всё сделать «в лоб»:
Видно, что сходимость метода – на 2 порядка выше (погрешность найденного решения
Наконец, существует метод хорд, в котором кривая f(x) заменяется прямой линией (хордой), стягивающей точки (a, f(a)) и (b, f(b)) . Формула этого метода зависит от знака выражения f(a)*f”(a) , то есть, имеет два варианта:
Если f(a)*f”(a)>0 , то x =b , xk+1=a-(f(a)(xk-a))/(f(xk)-f(a))
Если f(a)*f”(a) , то x =a , xk+1=xk-(f(xk)*(b-xk))/(f(b)-f(xk))
Вот примерная реализация на MathCAD, как и в предыдущих двух случаях, контролируется максимальное число итераций, равное 10000:
Видно, что сходимость метода оказалась в нашем случае не столь высока.
Подсчитать, сколько шагов какому методу потребовалось, можете сами, немного поменяв выдачу подпрограмм.

05.09.2013, 15:07; рейтинг: 72153
В этом методе нелинейная функция f(x) на отделенном промежутке
[a,b] заменяется хордой, проходящей через точки (a,f(a))и (b,f(b))
Рис.2.4. Метод хорд. Неподвижен правый конец промежутка b
Уравнение хорды: 
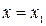
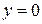
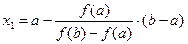
Точку x1 принимаем за новую границу отрезка, где содержится корень. Через эту точку с координатами (x1,f(x1)) и соответствующую границу предыдущего интервала (b,f(b)) опять проводим хорду, находим 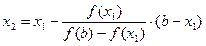
Вторая производная 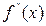
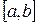
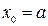
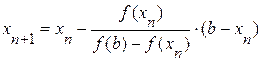
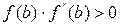
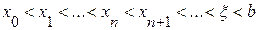
Рис.2.5. Метод хорд. Неподвижен левый конец промежутка a
Если f(a)·f «(a)>0, то хорда имеет левый фиксированный конец, причем последовательность x ,x1,…xn … приближается к корню справа. За начальное приближение x , берут b
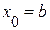
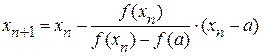
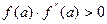
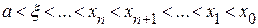
Для оценки точности можно воспользоваться формулой
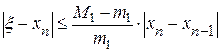
где 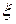
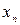
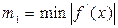
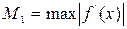
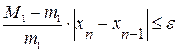
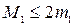
Пример 2.4. Найти методом хорд корень уравнения x 4 -x-1=0
Решение находим, используя пакет Mathcad.
Функция монотонна на промежутках (-∞, 0.63), (0.63, ∞) и меняет на концах промежутков знак. Уравнение имеет два корня. Сузим промежутки отделения корней методом проб, т.е. подстановкой.
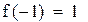 |
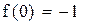 |
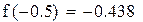 |
Первый корень принадлежит промежутку (-1,-0.5)
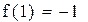 |
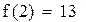 |
Второй корень принадлежит промежутку (1,1.5)
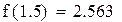 |
Будем находить корень на промежутке (-1,-0.5)
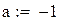 |
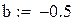 |
Вторая производная всюду положительна, функция положительна в точке a = -1, значит, этот конец неподвижен.
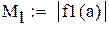 |
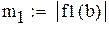 |
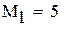 |
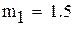 |
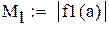 |
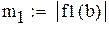 |
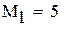 |
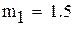 |
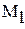 -максимальное, a -максимальное, a 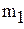 -минимальное значение модуля производной на промежутке -минимальное значение модуля производной на промежутке |
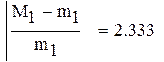 |
так как 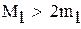
нужно учитывать при оценке точности решения,
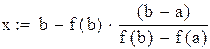 |
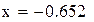 |
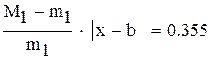 |
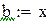 |
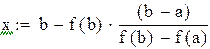 |
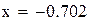 |
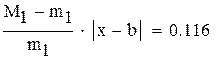 |
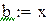 |
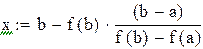 |
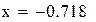 |
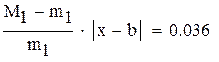 |
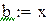 |
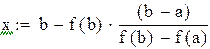 |
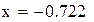 |
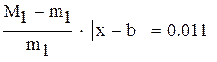 |
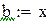 |
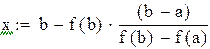 |
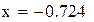 |
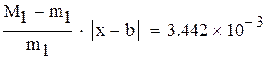 |
Нашли корень исходного уравнения 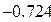
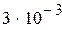
Рис. 2.6. Вычисления в Mathcad, реализующие метод хорд для примера 2.4
2.2.3. Метод Ньютона – метод касательных
Пусть 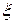
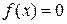
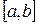
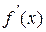
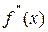
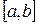
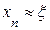
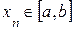
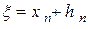

Ограничимся двумя членами ряда и так как 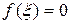
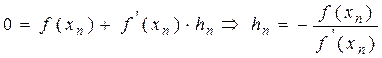
Учитывая найденную поправку hn:,получим 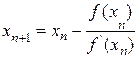
Рис.2.7 Метод касательных. Начальное приближение x =b
По-другому этот метод называется методом касательных. Если в точке 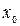
Хорошим начальным приближением 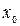
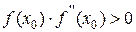
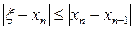
Теорема 2.2: Если 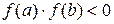
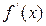
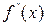
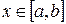
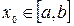
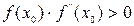
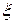
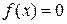
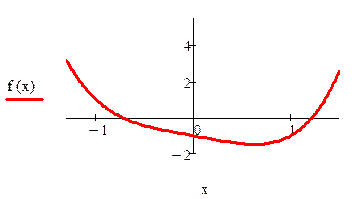
Пример 2.5. Найти методом Ньютона корень уравнения x 4 -x-1=0,
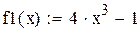 |
| 1-я производная |
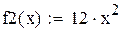 |
| 2-я производная положительна |
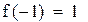 |
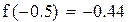 |
| один корень лежит на промежутке (-1.-0.5), второй на промежутке (1.1.5) Уточним левый корень методом Ньютона |
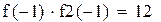 |
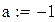 |
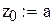 |
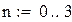 |
 |
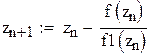 |
 |
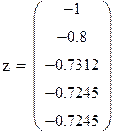 |
Нашли корень исходного уравнения -0.7245 с точность 0.00007.
Рис. 2.8. Вычисления в Mathcad, реализующие метод касательных для примера 2.5
Видео:Решение нелинейного уравнения методом деления отрезка пополамСкачать

Численные методы решения нелинейных уравнений. Метод хорд.
Метод хорд ( метод также известен как Метод секущих ) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения 

В отличие от метода половинного деления, метод хорд предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс (ось – Х). Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.
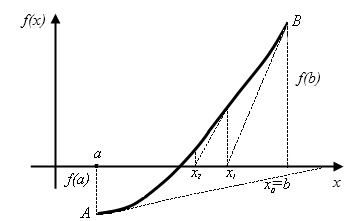
Геометрически метод хорд эквивалентен замене кривой 


Рис.1. Построение отрезка (хорды) к функции 
Уравнение прямой (хорды), которая проходит через точки А и В имеет следующий вид:
Данное уравнение является типовым уравнением для описания прямой вы декартовой системе координат. Наклон кривой задается по ординате и абсциссе с помощью значений в знаменателе 

Для точки пресечения прямой с осью абсцисс 
В качестве нового интервала для прохождения итерационного процесса выбираем один из двух 




Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности, т.е.

Рис.2. Пояснение к определению погрешности расчета.
Следует отметить, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.
Алгоритм нахождения корня нелинейного уравнения по методу хорд
1. Найти начальный интервал неопределенности 


2. Найти точку пересечения хорды с осью абсцисс:
3. Необходимо найти значение функции 



– если выполняется условие 


– если выполняется условие 


В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:
4. Проверяем приближенное значение корня уравнения на предмет заданной точности, в случае:
– если разность двух последовательных приближений станет меньше заданной точности 
– если разность двух последовательных приближений не достигает необходимой точности 

В качестве примера, рассмотрим решение нелинейного уравнения 


Вариант решения нелинейного уравнения в программном комплексе MathCAD .
Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.1).
Рис.1. Результаты расчета по методу хорд
Для обеспечения заданной точности 


Примечание:
Модификацией данного метода является метод ложного положения ( False Position Method ), который отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.
Следует отметить, что в случае если от нелинейной функции можно взять вторую производную 

Случай №1: 
Из первого условия получается, что неподвижной стороной отрезка является – сторона a .
Случай №2: 
Из второго условия получается, что неподвижной стороной отрезка является – сторона b .
В общем виде, для выявления неподвижного конца можно записать следующее условие: 


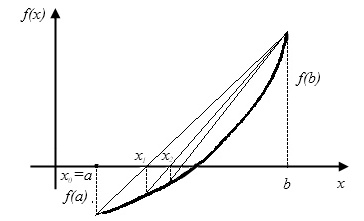
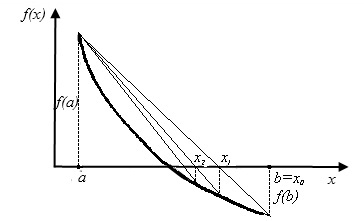
Рис. 3. Примеры убывающей или возрастающей функции
Таким образом, в зависимости от вида функции получаются два выражения для упрощения поиска корня функции:
– если функция соответствует первому случаю (см. рис. 3), тогда формула будет иметь следующий вид:

– если функция соответствует второму случаю (см. рис. 3), тогда формула будет иметь следующий вид:

Случай 

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
📺 Видео
Найти корень уравнения на заданном интервале (MathCad)Скачать

6 Метод половинного деления C++ Численные методы решения нелинейного уравненияСкачать

5 Метод половинного деления Блок-схема Численные методы решения нелинейного уравненияСкачать

Mathcad-09. Пример: уравненияСкачать

Урок 10. C++ Метод половинного деленияСкачать

Решение нелинейного уравнения методом половинного деления (дихотомии)Скачать