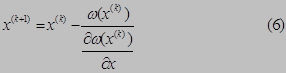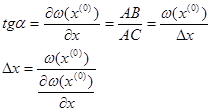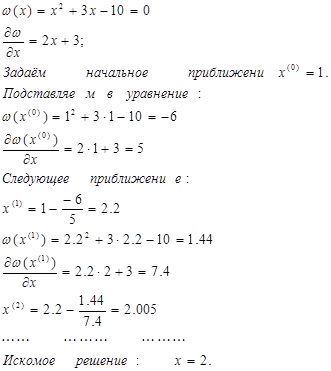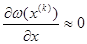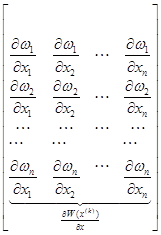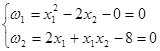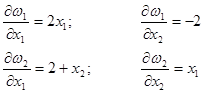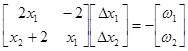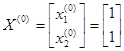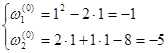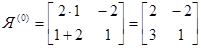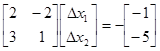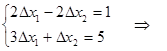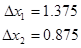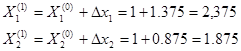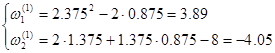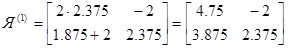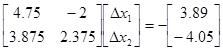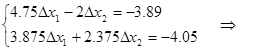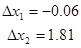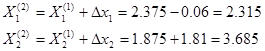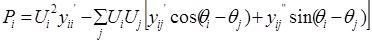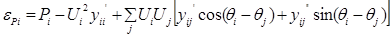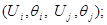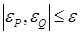Решение нелинейных уравнений методом Ньютона
Для решения электроэнергетических задач существует несколько моди-фикаций метода. Они позволяют увеличить скорость сходимости итераци-онного процесса и уменьшить время расчета.
Основное достоинство метода – он обладает быстрой сходимостью.
Идея метода состоит в последовательной замене на каждой итерации расчета исходной нелинейной системы уравнений некоторой вспомогатель-ной линейной системой уравнений, решение которой позволяет получить очередное приближение неизвестных, более близкое к искомому решению (линеаризация).
Рассмотрим нелинейное уравнение в общем виде:
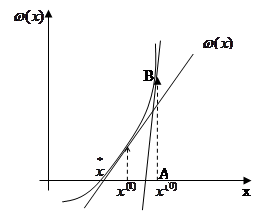
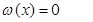
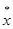
Задаем начальное приближение неиз-вестной х (0) . Определяем значение функции в этой точке w(х (0) ) и проводим касательную к кривой в точке В. Точка пересечения этой касательной с осью абсцисс определяет сле-дующее приближение неизвестной х (1) и т.д.
Разложим уравнение (1) в ряд Тейлора в окрестностях точки х (0) . Рас-смотрим члены разложения, содержащие только 1-ю производную:
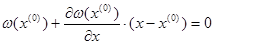
х – х (0) = Δх — поправка к неизвестной. Если определим её, то сможем определить и следующее приближение.
Из (2) определяем поправку 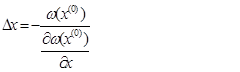

Тогда следующее приближение: 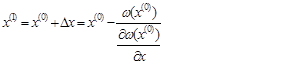
Аналогично получаем к-е приближения:
Это рекуррентная формула метода Ньютона для решения нелинейных уравнений. Она позволяет определять очередные приближения неизвестных.
Формулу (6) можно получить другим способом из рисунка:
Итерационный процесс сходится, если 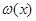
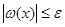
Комментарий к геометрической интерпретации
Итерационный шаг метода сводится к замене кривой 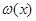
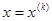
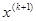
Для того, чтобы определить этим методом все корни нелинейного урав-нения, нужно любым способом определить приблизительное расположение этих корней и задать начальные приближения в близи них.
Простой способ определения области расположения корней — табуляция.
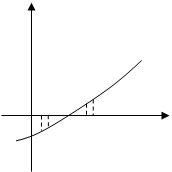
Процесс или не сходится или сходится очень плохо.
Метод Ньютона-Рафсона для решения СНАУ
Рафсон показал, что итерационный метод Ньютона, предложенный для решения одного нелинейного уравнения, можно использовать для решения систем нелинейных уравнений.
При этом, для решения систем нелинейных уравнений нужно вместо од-ной неизвестной рассматривать совокупность(вектор) неизвестных:
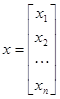
вместо одной невязки уравнения, рассматриваем вектор невязок уравнений системы:
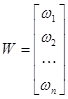
Одна производная в (6) замещается матрицей производных 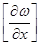
Рассмотрим систему действительных нелинейных алгебраических уравне-ний:
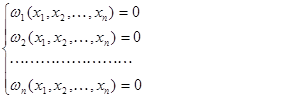
В матричном виде ее можно записать:
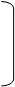
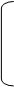

где Х = х2 – вектор – столбец неизвестных;
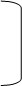
Пусть 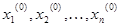

В результате получили систему линейных уравнений (линеаризованная система), в которой неизвестными являются поправки 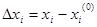
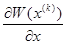
Каждая строка матрицы состоит из первых производных от очередного урав-нения нелинейной системы по всем неизвестным.
Запишем линеаризованную систему (9) в матричной форме:
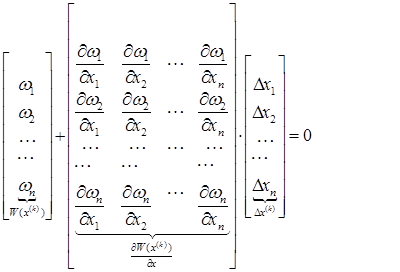
Здесь 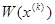
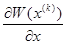
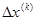
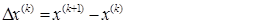
Систему (10) с учетом принятых обозначений можно записать:
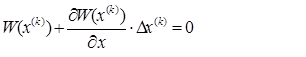
или 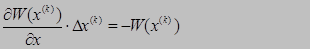
Эта система линейна относительно поправок ΔХ (к) .
Система (13) — линеаризованная система уравнений, которой заменяется исходная СНАУ на каждом шаге итерационного процесса.
Система (13) решается любым известным способом, в результате находим вектор поправок 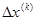
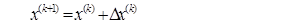
Т.о. каждый шаг итерационного процесса состоит в решении линейной сис-темы (13) и определении очередного приближения из (14).
Из (11) и (12) можно получить общую рекуррентную формулу (в матричном виде), соответствующую методу Ньютона–Рафсона:
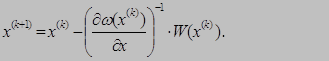
Она имеет структуру, соответствующую формуле (6).
Формула (15) в практических расчетах используется редко, так как здесь нужно обращать матрицу Якоби (большой размерности) на каждой итерации расчетов. В реальных расчетах поправки определяются в результате решения линейной системы (13).
Контроль завершения итерационного процесса выполняем по вектору невязок:
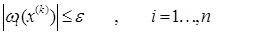
Это условие должно выполняться для невязок всех уравнений системы.
Алгоритм решения СНАУ методом Ньютона-Рафсона
1. Задание вектора начальных приближений неизвестных 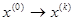
Задание точности расчета є , других параметров расчета
2. Определение невязок нелинейных уравнений в точке приближения 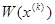
2.3. Определение элементов матрицы Якоби в точке очередного прибли-жения неизвестных 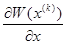
2.4. Решение линеаризованной системы (13) любым известным методом. Определение поправок к неизвестным 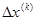
2.5. Определение очередного приближения неизвестных 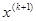
2.6. Контроль завершения итерационного процесса в соответствии с (16). Если условие не выполняется, то возврат к пункту 2.
Решить СЛАУ методом Ньютона-Рафсона:
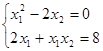
Запишем уравнения в виде невязок:
Определяем элементы матрицы Якоби:
Матрица Якоби:
Линеаризованная система уравнений:
Реализуем алгоритм метода Ньютона-Рафсона:
1) Первая итерация:
Начальные приближения
Невязки
Матрица Якоби:
Линеаризованная система уравнений:
1-е приближение неизвестных:
2) Вторая итерация
3) Третья итерация:
Решение систем уравнений установившегося режима методом Ньютона-Рафсона
Нелинейное уравнение установившегося режима в форме баланса мощ-ности для 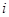
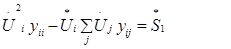
Это уравнение с комплексными неизвестными и коэффициентами. Для того, чтобы такие уравнения вида (17) можно было решать методом Ньюто-на-Рафсона, их преобразуют: разделяют действительные и мнимые части. В результате этого каждое комплексное уравнение вида (17) распадается на два действительных уравнения, которые соответствуют балансу активной и ре-активной мощности в узле:
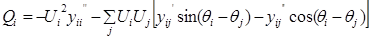
Здесь 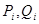
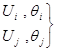
определить в результате расчета.
В правой части уравнений (18) — расчетная суммарная мощность пере-токов в ветвях, подходящих к 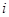
Запишем эти уравнения (18) в виде невязок:
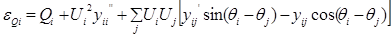
Невязки уравнений (19) соответствует расчетному небалансу активной и реактивной мощности в 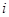
Невязки 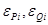
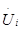
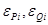
Будем решать методом Ньютона-Рафсона систему 2n уравнений вида (19), то есть для решения задачи расчета установившегося режима электри-ческой сети методом Ньютона — Рафсона нужно:
1) сформировать систему 2n уравнений вида (19) для всех узлов электрической сети, кроме балансирующих;
2) организовать итерационный процесс метода Ньютона-Рафсона
для решения этой системы уравнений. В результате решения
получаем искомые составляющие напряжений в узлах 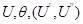
Запишем эту систему уравнений в общем виде:

Получили систему 2 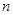
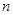
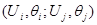
Для решения системы (20) методом Ньютона-Рафсона нужно составить вспомогательную линеаризованную систему уравнений вида (13), решая ко-торую на каждой итерации, определяем поправки к неизвестным:
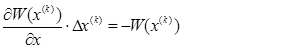
С учетом принятых обозначений система (21) может быть записана:
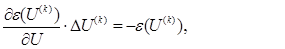
где 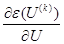
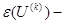
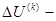
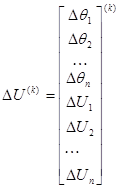
Для определения элементов матрицы Якоби применяем аналитическое дифференцирование, т.е. дифференцируем каждое уравнение системы (20) по искомым величинам – углам и модулям напряжений. Чтобы сформировать матрицу Якоби, нужно получить аналитические выражения для производных следующих видов:
1) Производная от уравнения невязки активной мощности 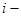
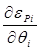
2) Производная от уравнения невязки активной мощности 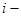
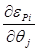
3) Производная от невязки активной мощности 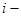
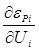
4) Производная от невязки активной мощности 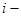
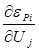
Аналогично определяются ещё четыре вида производных – производные от уравнений невязки реактивной мощности 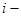
5) 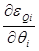
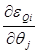
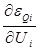
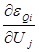
С учетом этих производных матрицу Якоби можно записать в общем виде:
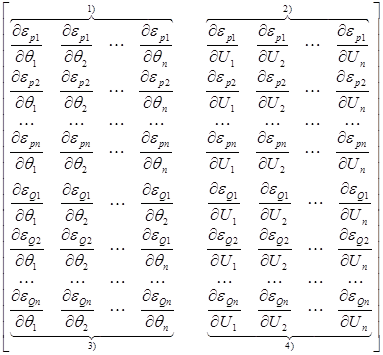
Определим аналитические выражения для производных, дифференци-руя уравнения системы (20) по неизвестным величинам. Они имеют вид:
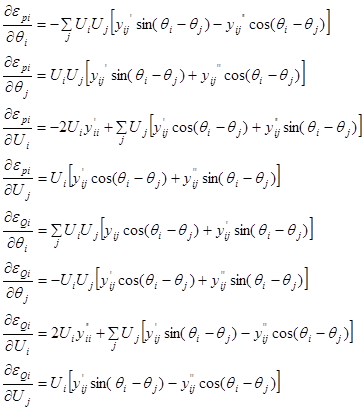
Матрица Якоби в общем случае — квадратная матрица, симметричная, размерностью 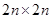
Если узлы 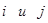
Каждая строка матрицы – это производные от очередного уравнения системы (20).
Наличие в схеме моделируемой сети особых узлов (опорные и балансирую-щие узлы, узлы ФМ) сказывается на структуре системы уравнений устано-вившегося режима и на структуре матрицы Якоби:
1. Для узлов с фиксацией модуля напряжения (ФМ), в которых заданы 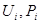
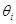
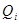
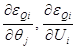
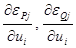
2. Для узлов опорных и балансирующих – соответствующие строки и столбцы матрицы исключаются;
3. Если узлы не связаны непосредственно – соответствующие произ-водные в матрице равны нулю.
Матрицу Якоби можно разбить на четыре блока:
1) 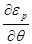
2) 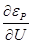
3) 
4) 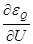
Это матрицы-клетки частных производных небалансов активной и реактив-ной мощностей по неизвестным углам и модулям напряжений. В общем случае, это квадратные матрицы размерностью n×n.
С учетом этого, матрица Якоби может быть представлена в виде блочной мат-рицы:
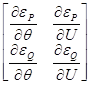
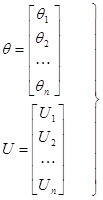
С учетом этого,Тогда линеаризованную систему уравнений (22) можно запи-сать в ви-де:
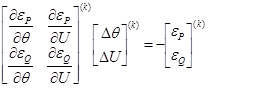
Решая эту линейную систему уравнений (любым известным методом) на
кКаждой итерации метода, находим поправки к неизвестным 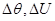
очередные приближения неизвестных:
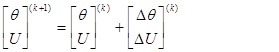
Очередное приближение неизвестных можно, также, получить с использо-ванием итерационной формулы метода Ньютона-Рафсона, аналогичной (15):
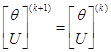
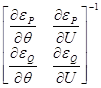
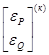
Тут требуется обращение матрицы Якоби на каждой итерации – громоздкая вычислительная операция.
Алгоритм решения систем уравнений установившегося режима методом Ньютона — Рафсона
1. Задание начальных значений неизвестных напряжений 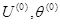
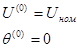
2. Задание условий расчета: точность ε, предельное количество итера-ций 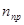
3. Определение невязок уравнений 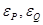
4. Определение элементов матрицы Якоби 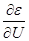
5. Решение линеаризованной системы уравнений (25) и определение поправок к неизвестным 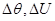
6. Определение очередных приближений неизвестных 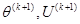
7. Проверка завершения итерационного процесса:
Значения невязок уравнений для всех узлов должны быть меньше задан-ной точности.
Если условие не выполняется, то возврат к пункту 3 и повторение рас-чета при новых приближениях неизвестных.
Существует ряд модификаций метода Ньютона-Рафсона. В том числе:
1. Модифицированный метод Ньютона-Рафсона.
Матрицу Якоби рассчитывают один раз при начальных значениях неизвест-ных. На последующих итерациях она принимается постоянной. Это значи-тельно сокращает объем вычислений на каждой итерации, но увеличивает ко-личество итераций.
2. Разделенный метод Ньютона-Рафсона.
Производные вида 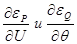
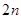
Дата добавления: 2015-10-05 ; просмотров: 6375 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Метод касательных (метод Ньютона)Скачать

5.2.1. Метод Ньютона–Рафсона
Идея метода заключается в линеаризации уравнений системы (5.1), что позволяет свести исходную задачу решения СНУ к многократному решению системы линейных уравнений.
Рассмотрим, как были получены расчетные зависимости метода.
Пусть известно приближение xi(k) решения системы нелинейных уравнений xi*. Введем в рассмотрение поправку Dxi как разницу между решением и его приближением:

Подставим полученное выражение для xi* в исходную систему.
Неизвестными в этой системе нелинейных уравнений являются поправки Dxi. Для определения Dxi нужно решить эту систему. Но решить эту задачу так же сложно, как и исходную. Однако эту систему можно Линеаризовать, и, решив ее, получить Приближенные значения поправок Dxi для данного приближения, т. е. Dxi(k). Эти поправки не позволяют сразу получить точное решение 


Для линеаризации системы следует разложить функцию fi в ряды Тейлора в окрестности xi(k), ограничиваясь первыми дифференциалами.
Полученная система имеет вид:


Все коэффициенты этого уравнения можно вычислить, используя последнее приближение решения xi(k). Для решения системы линейных уравнений (5.15) при n=2,3 можно использовать формулы Крамера, при большей размерности системы n – метод исключения Гаусса.
Значения поправок используются для оценки достигнутой точности решения. Если максимальная по абсолютной величине поправка меньше заданной точности e, расчет завершается. Таким образом, условие окончания расчета:
δ =
Можно использовать и среднее значение модулей поправок:
В матричной форме систему (5.15 ) можно записать как:




W(X(k)) – матрица Якоби, вычисленная для очередного приближения.
F(X(k)) – вектор-функция, вычисленная для очередного приближения.
Выразим вектор поправок ∆X(k) из (5.16):
Где W-1 – матрица, обратная матрице Якоби.
Окончательно формула последовательных приближений метода Ньютона решения СНУ в матричной форме имеет вид:

Достаточные условия сходимости для общего случая имеют очень сложный вид, и на практике проверяются редко. Нужно отметить, что метод сходится очень быстро (за 3 – 5 итераций), если det|W| ¹ 0 и начальное приближение X(0) выбрано близким к решению (отличаются не более чем на 10%).
Алгоритм решения СНУ методом Ньютона состоит в следующем:
1. Задается размерность системы n, требуемая точность ε, начальное приближенное решение X = (xi)n.
2. Вычисляются элементы матрицы Якоби W = (¶¦i ¤ ¶xj)n, n.
3. Вычисляется обратная матрица W-1.
4. Вычисляется вектор функция F=(fi)n, 

5. Вычисляются вектор поправок
6. Уточняется решение
7. Оценивается достигнутая точность δ= 
8. Проверяется условие завершения итерационного процесса
Если оно не соблюдается, алгоритм исполняется снова с пункта 2.
Для уменьшения количества арифметических действий Рафсон предложил не вычислять обратную матрицу W-1, а вычислять поправки как решение СЛУ (5.15)
Схема алгоритма метода Ньютона — Рафсона представлена на рис.5.2. При разработке схемы учтена необходимость защиты итерационного цикла от зацикливания: введен счетчик итераций k и ограничение на число итераций kmax (на практике не более 100).
Видео:Метод Ньютона | Лучший момент из фильма Двадцать одно 21Скачать

Метод Ньютона
Единственные требования, накладываемые на функцию $f$ — что у неё есть хотя бы один корень и что она непрерывна и дифференцируема на интервале поиска.
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

#Описание алгоритма
Алгоритм начинает с какого-то изначального приближения $x_0$ и затем итеративно строит лучшее решение, строя касательную к графику в точке $x = x_i$ и присваивая в качестве следующего приближения $x_$ координату пересечения касательной с осью $x$. Интуиция в том, что если функция $f$ «хорошая», и $x_i$ уже достаточно близок к корню, то $x_$ будет ещё ближе.
Чтобы получить точку пересечения для $x_i$, нужно приравнять уравнение касательной к нулю:
$$ 0 = f(x_i) + (x_ — x_i) f'(x_i) $$ откуда можно выразить $$ x_ = x_i — frac $$
Метод Ньютона крайне важен в вычислительной математике: в большинстве случаев именно он используется для нахождения численных решений уравнений.
Видео:Методы решения систем нелинейных уравнений. Метод Ньютона. Численные методы. Лекция 14Скачать

#Поиск квадратных корней
В качестве конкретного примера рассмотрим задачу нахождения квадратных корней, которую можно переформулировать как решение следующего уравнения:
$$ x = sqrt n iff x^2 = n iff f(x) = x^2 — n = 0 $$ Если в методе Ньютона подставим $f(x) = x^2 — n$, мы получим следующее правило: $$ x_ = x_i — frac = frac $$
Если нам нужно посчитать корень с некоторой заданной точностью $epsilon$, можно на каждой итерации делать соответствующую проверку:
Алгоритм успешно сходится к правильному ответу для многих функций, однако это происходит надежно и доказуемо только для определенного множества функций (например, выпуклых). Другой вопрос — как быстра эта сходимость, если она происходит.
#Скорость сходимости
Запустим метод Ньютона для поиска квадратного корня $2$, начиная с $x_0 = 1$, и посмотрим, сколько первых цифр оказались правильными после каждой итерации:
Можно заметить, что число корректных цифр примерно удваивается после каждой итерации. Такая прекрасная скорость сходимости не просто совпадение.
Чтобы оценить скорость сходимости численно, рассмотрим небольшую относительную ошибку $delta_i$ на $i$-ой итерации и посмотрим, насколько меньше станет ошибка $delta_$ на следующей итерации.
$$ |delta_i| = frac $$ В терминах относительных ошибок, мы можем выразить $x_i$ как $x cdot (1 + delta_i)$. Подставляя это выражение в формулу для следующей итерации и деля обе стороны на $x$ получаем $$ 1 + delta_ = frac (1 + delta_i + frac) = frac (1 + delta_i + 1 — delta_i + delta_i^2 + o(delta_i^2)) = 1 + frac + o(delta_i^2) $$
Здесь мы разложили $(1 + delta_i)^$ в ряд Тейлора в точке $0$, используя предположение что ошибка $d_i$ мала: так как последовательность $x_i$ сходится к $x$, то $d_i ll 1$ для достаточно больших $n$.
Наконец, выражая $delta_$, получаем
что означает, что относительная ошибка примерно возводится в квадрат и делится пополам на каждой итерации, когда мы уже близки к решению. Так как логарифм $(- log_ delta_i)$ примерно равен числу правильных значимых цифр числа $x_i$, возведение ошибки в квадрат соответствует удвоению значимых цифр ответа, что мы и наблюдали ранее.
Это свойство называется квадратичной сходимостью, и оно относится не только к нахождению квадратных корней. Оставляя формальное доказательство в качестве упражнения, можно показать, что в общем случае
$$ |delta_| = frac cdot delta_i^2 $$ что означает хотя бы квадратичную сходимость при нескольких дополнительных предположениях, а именно что $f'(x)$ не равна нулю и $f»(x)$ непрерывна.
🌟 Видео
Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

Метод Касательных - ВизуализацияСкачать

Численный метод Ньютона в ExcelСкачать

Вычислительная математика. Метод касательных на Python(1 практика).Скачать

15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Метод касательных (алгоритм Ньютона) на C#Скачать

10 Метод Ньютона (Метод касательных) C++ Численные методы решения нелинейного уравненияСкачать

Метод Ньютона, или Извлечение квадратного корняСкачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Сам себе программист Изучаю Python с нуля в свои 55! Исследование операций Метод Ньютона-Рафсона.Скачать

Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать

Численное решение уравнений, урок 4/5. Метод касательных (Ньютона)Скачать

Метод Ньютона для решения нелинйеных уравнений в MS ExcelСкачать

Метод Ньютона (Метод касательных)Скачать

10 Численные методы решения нелинейных уравненийСкачать

1 4 Метод Ньютона касательныхСкачать