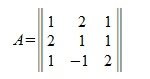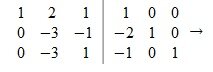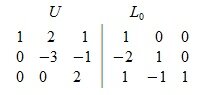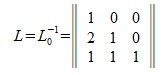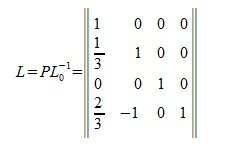Пусть система уравнений задается в виде:
Пример №1 . Дана система линейных уравнений. Решить ее методом LU-разложения.
Решение. Алгоритм декомпозиции основан на идее представления исходной матрицы в виде произведения двух треугольных матриц. Пусть задана квадратная матрица:
Представим A в виде: A=BC
Покажем пример вычислений нескольких значений матриц B и C.
Вычисляем значение элемента b11=1
c11=1/1=1
c12=3/1=3
c13=3/1=3
Вычисляем значение элемента b21=1
Вычисляем значение элемента b22=-2 — (1 • 3)=-5
c22=-5/(-5)=1
c23=0/(-5)=0
Вычисляем значение элемента b31=3
Вычисляем значение элемента b32=3 — (3 • 3)=-6
Вычисляем значение элемента b33=-1 — (3 • 3 -6 • 0)=-10
c33=-10/(-10)=1
| B= |
|
| C= |
|
Вычисляем значения yi
y1 = 11/1 = 11
y2 = (1 — 1 • 11 )/(-5) = 2
y3 = (1 — 3 • 11 -6 • 2 )/(-10) = 2
Вычисляем значения xi
x3 = y3 = 2
x2 = 2 — (0 • 2 ) = 2
x1 = 11 — (3 • 2 + 3 • 2 ) = -1
Пример №2 . Решить систему уравнений Ax = b методом Гаусса (LU-разложения).
Видео:LU разложение матрицыСкачать

Решение СЛАУ методом LU-разложения
LU-разложение — это представление матрицы A в виде A=L•U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. LU-разложение является модификациеё метода Гаусса. Основные применения данного алгоритма — решение систем алгебраических уравнений, вычисление определителя, вычисление обратной матрицы и др.
Рассмотрим алгоритм на примере матрицы
Алгоритм
- Создаем матрицы
и - Для каждого столбца j = 1… 3 матрицы
будем вычислять
как
Для каждой строки вычислим
Выполняем шаг 2 пока j
Видео:2_4. LU-разложениеСкачать

О песочнице
Это «Песочница» — раздел, в который попадают дебютные посты пользователей, желающих стать полноправными участниками сообщества.
Если у вас есть приглашение, отправьте его автору понравившейся публикации — тогда её смогут прочитать и обсудить все остальные пользователи Хабра.
Чтобы исключить предвзятость при оценке, все публикации анонимны, псевдонимы показываются случайным образом.
Видео:Линал 3.9. LU-разложениеСкачать

О модерации
Не надо пропускать:
- рекламные и PR-публикации
- вопросы и просьбы (для них есть Хабр Q&A);
- вакансии (используйте Хабр Карьеру)
- статьи, ранее опубликованные на других сайтах;
- статьи без правильно расставленных знаков препинания, со смайликами, с обилием восклицательных знаков, неоправданным выделением слов и предложений и другим неуместным форматированием текста;
- жалобы на компании и предоставляемые услуги;
- низкокачественные переводы;
- куски программного кода без пояснений;
- односложные статьи;
- статьи, слабо относящиеся к или не относящиеся к ней вовсе.
Видео:LU Разложение матрицыСкачать

LU-разложение. LUP-разложение
LU-разложение матрицы A — это представление матрицы A в виде произведения
Видео:Решение системы уравнений методом LU-разложения (устар.)Скачать

Процедура LU — разложения
Пусть A прямоугольная матрица порядка m×n любого ранга. С правой стороны матрицы А приписываем единичную матрицу E порядка m×m. Применяем к матрице A|E метод исключения Гаусса. Если на каком то этапе Гауссово исключения ведущий элемент равен нулю, и существует ненулевой элемент, расположенный ниже ведущего элемента, то LU — разложение данной матрицы невозможно. Если же элементы ниже ведущего элемента нулевые, то выбираем новый ведущий элемент той же строки и следующего столбца.
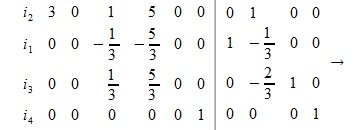
Приводим матрицу A|E к треугольному или ступенчатому виду. Получим матрицу U|L0, где U— верхняя треугольная или ступенчатая матрица, а L0— нижняя треугольная матрица. Заметим, что полученная матрица L0 приводит A к треугольному или ступенчатому виду:
Так как L0 квадратная невырожденная матрица, следовательно имеет обратную матрицу 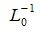
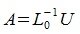 | (2) |
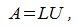 | (3) |
где 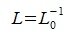
Как мы отметили, не всегда можно проводить LU -разложение матрицы. Но LUP— разложение всегда возможно.
LUP-разложение матрицы A — это представление матрицы A в виде произведения
где L-нижняя треугольная матрица, U — верхняя треугольная или ступенчатая матрица, P— матрица перестановок (матрица перестановок — эта матрица, полученная из единичной матрицы перестановкой некоторых строк или столбцов).
Видео:Решение системы уравнений методом LU-разложенияСкачать

Процедура LUP — разложения
Пусть A прямоугольная матрица порядка m×n любого ранга. С правой стороны матрицы А приписываем единичную матрицу E порядка m×m. Применяем к матрице A|E матод исключения Гаусса c выбором наибольшего по модулю ведущего элемента. Если на каком то этапе исключения ведущий элемент равен нулю, то процедуру останавливаем. Получим матрицу U|L 0. Тогда имеют место равенства (1) и (2). Но в общем случае L0 и, следовательно, 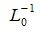
Далее допустим, что мы знаем, как построить матрицу A 1 из матрицы A переставляя строки так, что при применении Гауссово исключения c выбором максимального по модулю ведущего элемента относительно матрицы A 1 не понадобилась переставление строк. Выбираем матрицу перестановок так, что
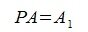 | (4) |
Строим матрицу A 1|E и применяем Гауссово исключение. Получим матрицу U|L 1. Тогда
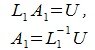 | (5) |
где L 1 и 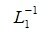
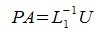 | (6) |
Обозначим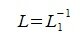
Наша задача найти L и U, без построения A 1.
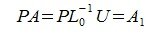 | (7) |
Тогда, учитывая второе равенство (5), получим:
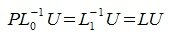 | (8) |
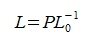 | (9) |
Получили, что для LUP-разложения нужно применить Гауссово исключение c выбором максимального по модулю ведущего элемента относительно матрицы A|E. Получим матрицу 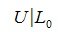
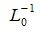
Матрица перестановок Р строится во время Гауссово исключения, учитывая перестановки строк.
Видео:Линейная алгебра Практика 4 LU-разложениеСкачать

Пример LU — разложения (A=LU)
Видео:LU-разложение. МатрицыСкачать

Пример LUP — разложения (PA=LU)
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

LU (LUP)-разложение онлайн
Для LU(LUP)-разложения онлайн пользуйтесь матричным онлайн калькулятором.
🎦 Видео
Решение системы уравнений Ax=b с помощью обратной матрицы.LU разложение. Нахождение обратной матрицыСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

А.7.34 LU-факториризация, LUP-факторизация и разложение ХолецкогоСкачать

Матричный метод решения систем уравненийСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Решение уравнений с помощью разложения на множители | Алгебра 7 класс #23 | ИнфоурокСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Методо Гаусса. LU-разложение.Скачать

Линейная алгебра Лекция 4 LU разложениеСкачать

Решение системы уравнений методом ГауссаСкачать

22.11.2021 ЧМЛА (МГТУ им. Баумана, формулировка задач - м. Холецкого, LU-разложение)Скачать