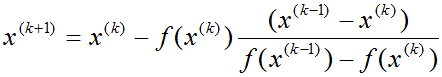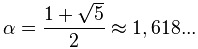Решение уравнений методом хорд python (4 видео)

Программирование на C, C# и Java

Содержание

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
Метод хорд
Метод хорд. Алгоритм
Метод хорд. Программная реализация
Chord (DHT) in Python
Introduction
Implementation
Experiments
Load Balance
Robustness to Node Failure
Conclusion
References
Метод хорд
Метод хорд
Метод хорд
📸 Видео

Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод хорд

Метод хорд используется для численного нахождения приближенного значения корня нелинейного уравнения. В данной статье будет показан алгоритм метода, а также будет приведена его программная реализация на языках: Си, C# и Java.

Метод хорд (то же, что метод секущих) — итерационный метод решения нелинейного уравнения.

Нелинейное уравнение — это уравнение в котором есть хотя бы один член, включающий неизвестное, НЕ в первой степени. Обозначается, как: f(x) = 0.

Метод хорд. Алгоритм

Метод хорд является итерационным алгоритмом, таким образом решение уравнения заключается в многократном повторении этого алгоритма. Полученное в результате вычислений решение является приближенным, но его точность можно сделать такой, какой требуется, задав нужное значение погрешности ε. В начале вычислений методом хорд требуется указать границы области поиска корня; в общем случае эта граница может быть произвольной.

Итерационная формула для вычислений методом хорд следующая:

Вычисления продолжаются до тех пор, пока не станет истинным выражение:

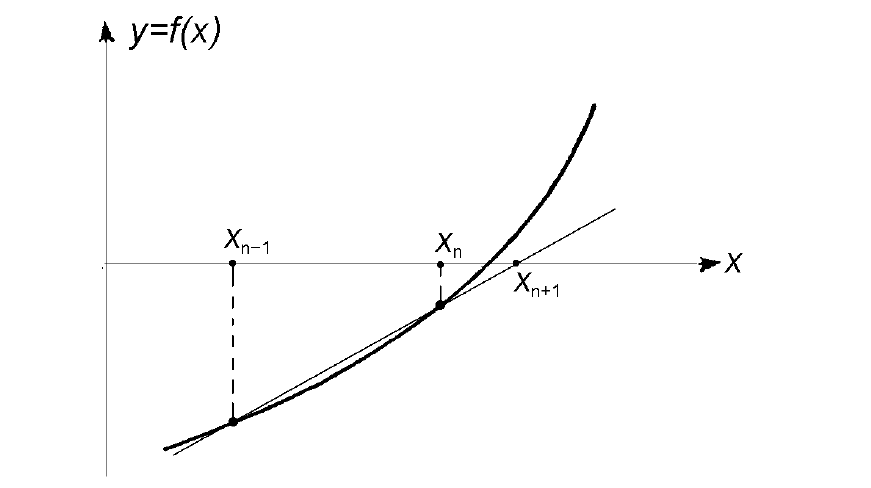
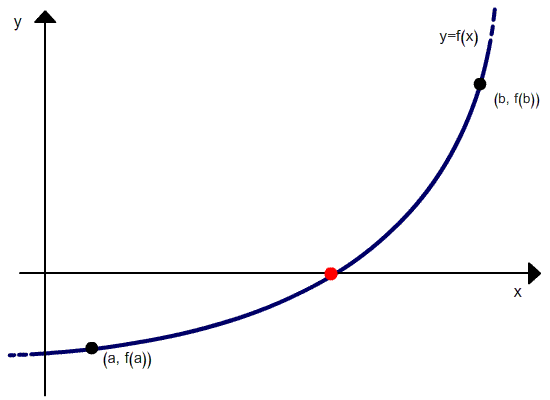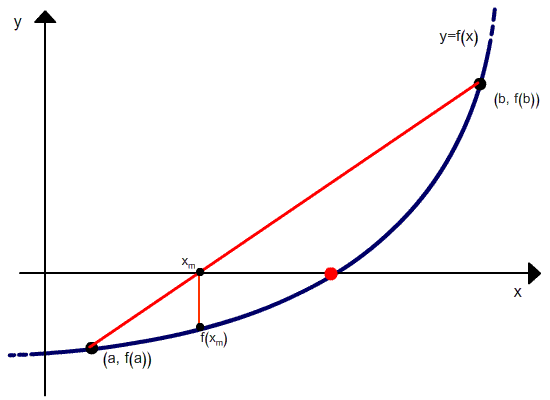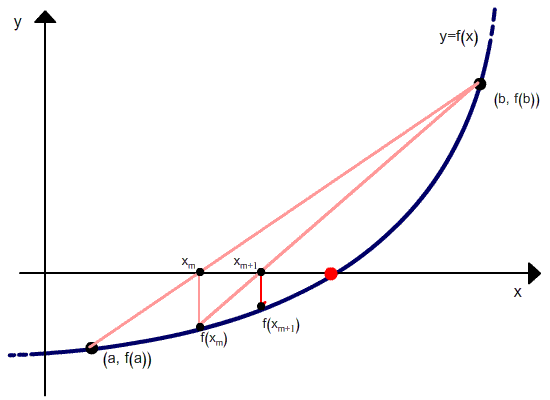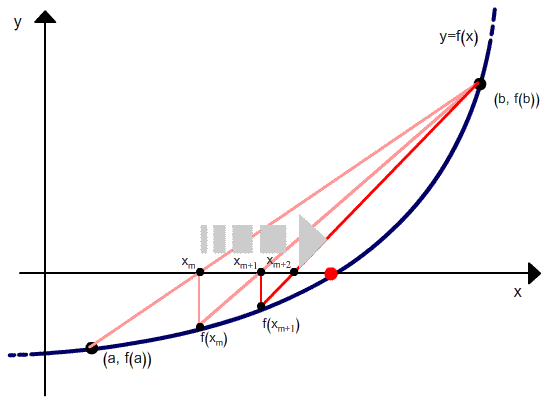
Геометрическая модель одного шага итераций метода хорд представлена на рисунке:

Метод хорд, в отличие от метода Ньютона, имеет плюс в том, что для расчета не требуется вычисление производных. Но при этом метод хорд медленнее, его сходимость равна золотому сечению:

Метод хорд. Программная реализация

Ниже мы приводим реализацию алгоритма метода хорд на языках программирования Си, C# и Java. Кроме того, исходники программ доступны для скачивания.

В качестве примера ищется корень уравнения x 3 — 18x — 83 = 0 в области x0 = 2, x1 = 10, с погрешностью e = 0.001. (Корень равен: 5.7051).

x_prev — это x_k-1, x_curr — это x_k, x_next — это x_k+1.

Видео:Алгоритмы. Нахождение корней уравнения методом хордСкачать

Chord (DHT) in Python

Authors: Ruairidh Battleday, Ethan Tseng, Felix Yu

Видео:Решение нелинейного уравнения методом хорд (секущих) (программа)Скачать

Introduction

Background
Chord is a Peer-to-Peer (P2P) protocol introduced in 2001 by Stoica, Morris, Karger, Kaashoek, and Balakrishnan. An ideal Peer-to-Peer system has no centralized control and no imbalance in responsibilities between nodes: each node serves the same purpose within the system. This allows for better distribution of workload throughout the system, and does not introduce a single point of failure. Chord, specifically, is a distributed hash table (DHT): an application of P2P systems that allows for fast lookup across a distributed system. Chord’s main contribution is the ability to achieve lookups in O(log N) steps, with each node only keeping track of O(log N) other nodes in the system.

Context and Related Work
At the time of Chord’s inception, P2P systems were often used for file-sharing, with applications such as Napster and Gnutella. However, Napster had a centralized look-up system, offering a single point of failure, and Gnutella had an inefficient flooding mechanism, which sent out O(N) queries per look-up. These design choices negatively impacted the scalability and security of these underlying systems; Chord resolved these shortcomings through alternative designs and routing schemes.

How Chord Achieves Scalability
Chord supports the lookup operation of mapping a key onto a node. With this operation, one can create a DHT: the key can be associated with a value, which is stored on the node that the key maps to. To achieve scalability, the mapping occurs in sublinear O(log N) number of look-ups, and each node also only stores routes to sublinear O(log N) other nodes.

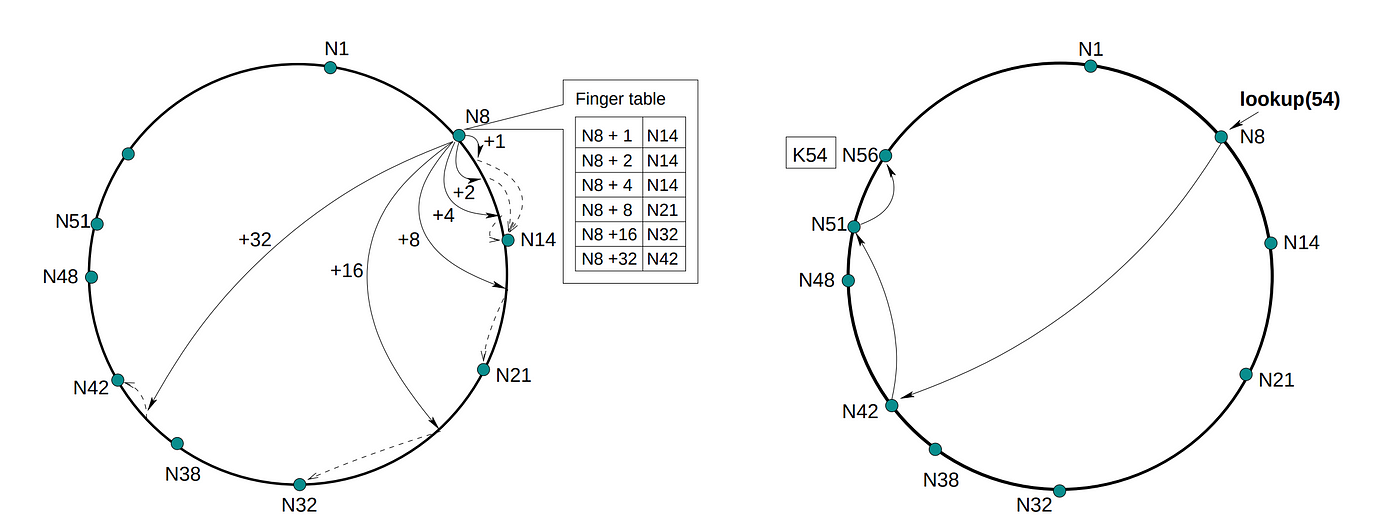
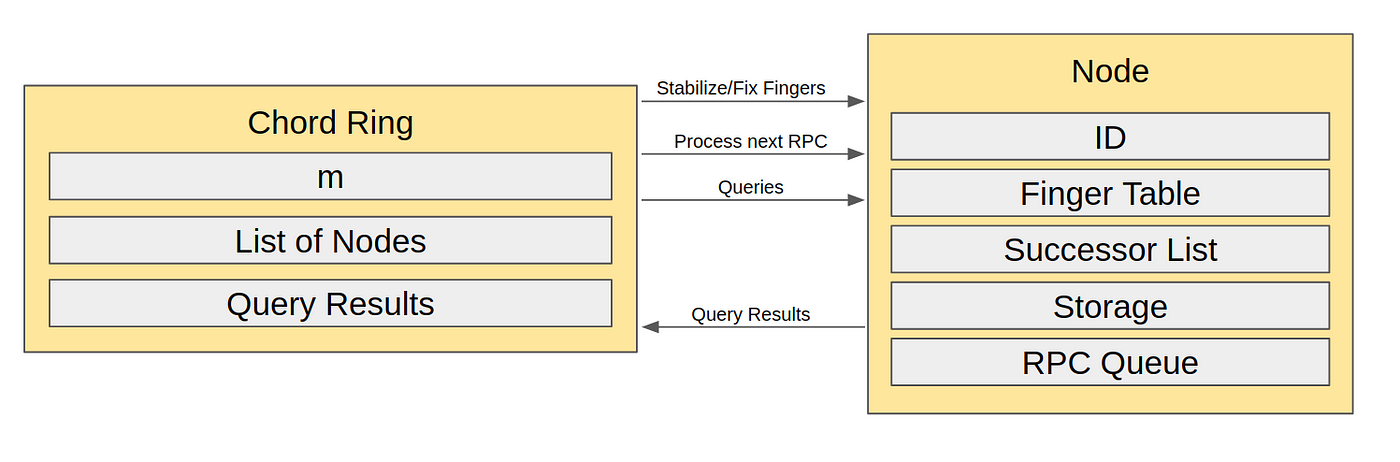
Chord’s structure can be described by a number line that contains 2ᵐ integer valued addresses between [0, 2ᵐ), where the line wraps around via the modulo operation. Thus, from here on, we will refer to the structure as the Chord Ring, with values increasing clockwise around the ring. Each Node is assigned an ID/position on this Chord Ring through the SHA-1 hash of its IP address. Similarly, each key is assigned an ID through its hash. The key is stored on its “successor”: the Node with the ID that directly succeeds it; in the case where the key has the same ID as a Node, the key is stored on that node.

A trivial method of locating the Node that stores a key is to move clockwise among the nodes until we find the Node ID that succeeds the key ID. However, this takes O(N) lookups, even though each Node only needs to keep track of it’s successor.

To achieve faster look-up, Chord uses the concept of a finger table. Each Node keeps track of up to m other Nodes in its finger table, where the iᵗʰ entry of the table is the Node that directly succeeds the ID of the Node + 2ⁱ. This allows for faster routing with O(log N) lookups, since rather than going to the next Node clockwise on the Chord Ring, a query can skip to a Node at least half the remaining distance to the true ID of the key.

How Chord Maintains Correctness
In order for this routing to work under a dynamic environment where Nodes are constantly joining and leaving, Nodes in Chord need to have accurate successor pointers and finger tables. Therefore, Nodes will occasionally stabilize by checking if a) their successor is still alive, and b) their successor is correct: its predecessor index points back to them. If either of these fail, Nodes will update their successors accordingly. Nodes will also occasionally fix their finger tables through the find_successor method to keep them up to date. To ensure a lookup doesn’t fail, each Node will also maintain a successor list that keeps track of its m direct successors nodes. If the direct successor is no longer alive, the Node will query subsequent successors until it finds one that is alive. Therefore, the lookup can only fail if no nodes in this list are alive, which is improbable. The successor list is maintained in the stabilize step.

Видео:Вычислительная математика. Метод касательных на Python(1 практика).Скачать

Implementation

Code Structure and Methodology
We implement a simulator for the Chord Peer-to-Peer (P2P) distributed system. Our goals for this project are to 1) obtain a better understanding of a real-world distributed system by implementing one ourselves and 2) to validate Chord’s theoretical and experimental results. Our implementation can handle both node joins and departures, including both graceful departures and voluntary failures. The code is available here.

Our simulator code is in Python and is algorithmic. Although it is implemented as an approximation of multiple nodes working in parallel, the actions of the nodes are executed serially. This is done by quantizing time in discrete units. At each unit of time, each Node performs one operation in round-robin fashion. Nodes communicate with each other by sending Remote Procedure Calls (RPCs), either containing return values or instructions to execute a function. These RPCs are “sent” by having the sender Node append the RPC onto the end of the receiver Node’s RPC queue.

To coordinate this simulation, we have the Chord Ring. The Chord Ring keeps track of all Nodes in the Ring by maintaining a list, and can add/remove Nodes as desired. At each time step, the Chord Ring will “step”, so each Node in the list processes one RPC. The serial order in which the Nodes do this is arbitrarily determined by their order in the list. Occasionally, the Ring will tell Nodes to stabilize/fix fingers, although it would have been entirely possible for the Node itself to keep track of this themselves as well. The Chord Ring also acts as the client in that it can add and query Nodes for keys, storing the results that Nodes send back.

Implementation Details
We use the following parameters for the periodic operations that each Node runs:

Stabilize: run every 200 steps;
Fix Fingers: fix one finger every 100 steps;
Check Predecessor: run every 300 steps;

We note that these timesteps were created with no latency in mind, and that if we had added some latency to the RPCs, these values would also need to be adjusted accordingly. We further stagger the periodic operations by having nodes that join the network wait for a random number of steps before beginning periodic operations.

Find Successor is implemented recursively. That is, rather than have the original Lookup Node initiate all Find Successor RPCs, the intermediate Nodes directly forward the query to the next relevant Node. Once the successor is found, the return message can be sent back directly to the original Node.

When a Node joins the network, it calls a random Node to find it’s successor. Once that successor is found, the Node will send an RPC to the successor to ask for key value pairs that this Node should store. The successor then sends those pairs in a return RPC.

To stabilize, the Node updates its successor (by finding the first alive node in the Successor List, and then looking at that node’s predecessor), and then notifies the new successor. Once the successor is found, the Successor List can be updated as well. We note that usually RPCs are required to find the first alive successor and its relevant values. However, it was not straightforward to implement receiving RPC messages within a function, so we directly looked at the Chord Ring for these values. This is an approximation that we are willing to make, since the number of RPCs needed for these exchanges is minimal.

Fix Finger is straightforward. Each time the function is called, the Node looks at the next finger to update, and starts a Find Successor call to update its value.

Departures from Standard Chord Implementations
We avoid the trouble of modelling extraneous factors such as packet level network delays and packet drops as the focus in the paper is not on routing latency, but rather on the scalability of Chord. As such, our simulator provides us with the necessary framework to evaluate Chord.

Since we do not deal with routing latency, we check whether a node is alive or not by directly looking at whether the node is in the Chord Ring.

Furthermore, since our implementation is serial, pseudo-parallelism can break down in cases where in a single timestep, a Node can send an RPC and a subsequent Node can immediately process it. However, since we focus on scalability of Chord, this approximation, again, does not affect our evaluation.

Our simulator also abstracts away the difference between real nodes and virtual nodes. Although real nodes may be tied to a location or IP address, virtual nodes can be assigned perfectly randomly. Our simulator uses uniform randomization to assign nodes to addresses, so our simulator is essentially only working with the virtual nodes. For the experimental section, we translate the bounds given in the paper for real nodes into bounds in terms of virtual nodes.

Видео:Метод хордСкачать

Experiments

With our Chord simulator in hand, we ran a series of experiments to empirically validate the theoretical claims in the paper. For these experiments we follow the theorems, definitions, and experimental setup as described in the full version of the paper: https://pdos.csail.mit.edu/papers/ton:chord/paper-ton.pdf
Experiments can be found in separate branches of our implementation.

Видео:Метод Хорд - ВизуализацияСкачать

Load Balance

Our first series of experiments focused on Chord’s load balancing guarantees. These are presented through the following three Theorems in the paper:

Theorem 1: For any set of N nodes and K keys, each node is responsible for at most(1 + log N) K / N keys with high probability.

Theorem 2: With high probability, the number of nodes that must be contacted to find a successor in an N-node network is O(log N).

Theorem 3: With high probability, any node joining or leaving an N-node Chord network will use O(log² N) messages to re-establish the Chord routing invariants and finger tables.

These theorems all derive their guarantees from consistent hashing. To perform consistent hashing, we simply utilize Python’s random number generator to generate random addresses.

In order to measure the number of “hops” for path lengths, we modify our simulator to have a hop tracker that increments by 1 each time a node forwards a find_successor RPC to another node. This step tracker is part of the RPC and is shuttled along with it.

Experimental Setup
For these experiments we perform the following procedure:

We add N nodes and K keys into a Chord ring and allow it to fully stabilize.
Measure the number of keys per node D.(Theorem 1).
Perform Q key queries to the Chord ring. Measure the mean path length L (Theorem 2).
Have a node join the Chord ring. Measure the number of messages M between that node and other nodes (Theorem 3).

We vary N and K and observe how D, L, M change. We also set the ring size R = 16 (addresses are in the range [0, 2¹⁶ — 1] ).

We run our simulator for N = [2⁴, 2⁵, 2⁶, 2⁷, 2⁸] and K = [2¹², 2¹³, 2¹⁴, 2¹⁵] and record the mean measurement and standard deviation across all trials. For each trial we randomize the node IDs and key addresses.

Keys per Node
In the plot below we show the maximum number of keys per node across 4 trials. The error bars show one standard deviation difference.

Reviewing the top panel, our experiments confirm that our implementation of Chord does indeed distribute keys in a near linear decreasing fashion; as expected, this relationship holds regardless of the number of keys. In the bottom panel, we review the key distribution over nodes from a single experiment. Here, we find a power-law distribution consistent with the results of the original Chord paper.

Mean Path Length
In the plot below, we show the average path length per 1000 queries for 4 trials. The error bars show one standard deviation differences across trials.

Our plot illustrates the logarithmic dependence of L on N, as expected from the Theorem and results in the Chord paper. We find that this relationship is not particularly affected when K — -the number of keys — -varies. This is in a sense unsurprising, as the key storage and look up operations are not measured by path length.

Number of messages upon node join
In the plot below we show the number of messages incurred upon a node join across 60 trials. The error bars show one standard deviation differences.

When analyzing the average number of messages sent by a joining node, the relationship between N and the average number of messages a joining node sends appears to be roughly exponential in log-log space. This is consistent with the expected O(log² N) message-per-node-join relationship given by the theorem — -a finding that could be strengthened by reviewing larger ranges over input variables in future work. We also see no dependence on K, as expected.

Видео:Решение n го нелинейных алгебраических уравнений в PythonСкачать

Robustness to Node Failure

From the previous experiments we see that Chord indeed has good load balance properties during normal operation. However, how tolerant is Chord to node failure (when nodes voluntarily leave the system)? To investigate this we performed a series of experiments using a similar setup as in the paper.

The paper utilizes the following definitions:

A timeout occurs when a node tries to contact a failed node. This occurs during the find_successor operation when a node traverses its finger table and its successor list to find the closest living predecessor to a specific key.
A failed lookup occurs when a query is unable to find the closest living successor to a target key. It is important to note that a lookup succeeds even if the found successor has not claimed the key yet (i.e. the key is currently owned by a departed node).

Simulator modifications to handle node failures
In the Chord paper, the term timeout was used because nodes would send pings to other nodes to check whether or not they were alive, and if no response was received after 500ms then the pinged nodes are considered to have failed. As we do not implement sending RPCs to failed or departed nodes, we instead count the number of timeouts by incrementing counters whenever a node pings a dead node to check their existence.

Timeouts do not consume any time in our simulator, but in a real implementation a node will be delayed by timeouts and may even re-ping failed nodes. This simplification is fine since the quantities we measure in our experiments are not affected by timeout delays.

Counting Timeouts
There are three locations in Chord where timeouts can occur, all of which are in the find_successor operation. The first location is when searching the successor list for the first living successor, each failed node that we ping along the way corresponds to a single timeout.

The second location is during traversal of the finger table to find the closest preceding node to a target key. As we search backwards through the finger table, whenever a potential predecessor node is found we check to see if that node is alive. If that node is dead, then we increment the number of timeouts. We first check to see if a node is a valid predecessor node before checking to see if it is alive, as performing the checks the other way around results in unnecessary timeouts.

It could be the case that all potential predecessor nodes in the finger table have failed. In that case, the third location where timeouts can occur is when searching backwards through the successor list for the closest living predecessor node to the target key.

The experiments we perform simulate worst case conditions for Chord. We are interested in the performance of Chord immediately after a large number of nodes fail and before Chord has fully stabilized. To simulate this, we perform the following procedure:

We add N nodes and K keys into a Chord ring and allow it to fully stabilize.
We then turn off periodic operation: stabilize, fix_fingers, check_predecessor.
For each node, cause it to fail with probability p.
Perform Q key queries to the Chord ring. Measure the number of timeouts T, number of failed lookups F, and the mean path length L.

We vary the failure probability p and observe how T, F, and L change. We fix N = 100, K = 1000 and Q = 500. We also fix the following hyperparameters:

Ring size R = 12 ( addresses are in the range [0, 2¹² — 1] )
Successor List Size r = 2 * ceil(log_2(N)) = 14. This size is necessary to obtain the theoretical guarantees in the paper.

We run our simulator for p = [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6] and for each value of p we take the record the mean measurement and standard deviation across 20 trials. For each trial we randomize the node IDs and key addresses.

We note that a pathological case occurs when all of the successors in a node’s successor list dies. This will not occur with high probability because we use a successor list size r = Omega(log_2(N)). Furthermore, if it does happen then Chord can no longer make progress since that node cannot execute fix_fingers or stabilize. Thus, when this case happens we simply restart the trial.

Timeouts vs Failure Probability

In the plot below we show the average number of timeouts per query across 20 trials. The error bars show one standard deviation differences.

We see similar scaling trends and increases in variance for both our experiments and the paper’s experiments. However, the number of timeouts we measured is larger than what is reported in the paper (shown in Table II). One possible reason is that in our experiments we do not update the finger tables or successor lists to mark that failed nodes have been pinged before. As such, a failed node may be pinged several times by the same node. The paper does not specify whether or not these updates are implemented as part of Chord, as these updates are optimizations on top of the primary Chord operations. We chose not to incorporate these updates in order to benchmark the worst case performance, which would be incurred by the first few queries to a Chord ring just after the failure when failed nodes have not been pinged yet.

Lookup Failures vs Failure Probability
There were zero lookup failures across all experiments and trials. This is in agreement with the paper’s experiments. The reason for this is because as long as each living node’s successor list contains at least one living node then progress can always be made towards finding the closest living successor of the target key.

Mean Path length vs Failure Probability
In the plot below we show the mean path length across 20 trials. The error bars show one standard deviation differences.

The paper proves that the relationship between Average Path length L and failure probability p is neither linear nor logarithmic, but L does grow slowly with respect to p. Our experimental results confirm this. We do see that the average path length scales upwards as the failure probability increases since more hops are required to bypass failed nodes. However, the increase is very slight and the error bars show that the mean path length does not vary widely.

Видео:Решение нелинейного уравнения методом Ньютона (касательных) (программа)Скачать

Conclusion

In this project, we implemented a purely algorithmic Chord simulator. Using this simulator we ran several of the same experiments from the paper and compared their results against our own.

Our Load Balancing results demonstrate Chord’s ability to scale well with increasing nodes and keys, and corroborate the results from the paper.

Our Robustness to Failure results showed that although the mean path length is small even in the face of large node failures, the number of timeouts per query grows significantly. This could be ameliorated by having nodes remember which failed nodes they have pinged before so that they do not ping them again. In doing this, only the first few queries will be slow, but future queries will complete in time proportional to the mean path length.

Regardless of state, there should be no case where a cycle forms (where a few nodes pass the same find_successor RPC to each other infinitely). However, we had this happen in our implementation. We found that this occurred because we used an inclusive-exclusive bound for the closest_preceding_node function, rather than the exclusive-exclusive bound stated in the pseudocode of the paper. In this case, if the RPC in question is finding a key that shares an ID with a Node, and this Node receives the find_successor RPC due to the bug (that Node’s predecessor should actually receive it in normal case behavior), it is possible that a cycle forms. Future attempts at implementing Chord should pay careful attention to bounds described in the pseudocode.

We also originally implemented the code in both Golang and Python, where Nodes opened channels to each other and waited for responses rather than send out RPCs. We found that this deadlocked even in simple cases (3 Nodes).

Видео:1,2 Решение нелинейных уравнений методом хордСкачать

References

Chord: A Scalable Peer-to-peer Lookup Service for Internet Applications
Ion Stoica; Robert Morris, David Karger, M. Frans Kaashoek, Hari Balakrishnan

Видео:СОБЕСЕДОВАНИЕ с Эдуардом | Знания Python, задачи на код, алгоритмические задачиСкачать

Метод хорд

Метод хорд — итерационный численный метод приближённого нахождения корня уравнения.

Немного теории о методе хорд под калькулятором.

Метод хорд

Метод хорд можно рассматривать как комбинацию метода секущих (Метод секущих) и метода дихотомии — отличие от метода секущих состоит в том, что если в методе секущих в качестве точек следующей итерации выбираются последние рассчитанные точки, то в методе хорд выбираются те точки, в которых функция имеет разный знак, и соответственно, выбранный интервал содержит корень.

Вывод итерационной формулы аналогичен выводу формулы для метода секущих:

Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет

Для точки пересечения с осью абсцисс (у=0) получим уравнение

Но в отличие от метода секущих, после расчета следующего приближения в качестве второй точки выбирается не последняя, а та, в которой функция имеет разный знак со значением функции в вычисленной точке. Проиллюстрировано это ниже.

Метод хорд является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале), при этом величина интервала в процессе итераций не стремится к 0.

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε. При этом имеется в виду не интервальные значения, а два вычисленных значения, так как величина интервала не стремится к 0.