Решение уравнений методом группировки примеры (4 видео)

Решение уравнения методами группировки и замены переменной

Содержание

Страницы работы
Содержание работы
Разложение многочлена способом группировки
Основные понятия
5 способов разложения многочлена на множители
Способ группировки множителей
Разложение способом группировки
Примеры разложения многочлена на множители
📺 Видео

Страницы работы

Содержание работы

Лабораторная работа №1

Цель работы: Решить уравнения методами:

б) замены переменной.

Теоретическая часть работы

Способ группировки разложение на множители

Для того, чтобы разложить многочлен 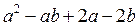на множители:

1 – Объединим слагаемые попарно в группы (говорят «сгруппируем слагаемые»): два в одну группу, и два — в другую .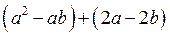

2 – В каждой паре вынесем за скобки общий множитель.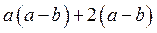

3 – Заметим, что оба полученных слагаемых также имеют общий множитель, который можно вынести за скобки .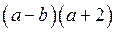

Не любая группировка приводит к разложению на множители. В случае неудачи попробуйте сгруппировать по-другому, или вообще попытайтесь применить другой метод.

Рассмотрим решение уравнения способом разложения на множители на конкретном примере:

Применив способ группировки, получим:

Помня, что произведение равно 0 в случае, если один из множителей равен 0, получим корни уравнения:

Метод введения новой переменной

Пример.

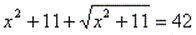
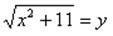
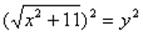
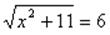
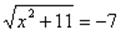
Введем новую переменную , учитывая, что , получаем квадратное уравнение у 2 +у – 42=0 , корни которого -7 и 6. Возвращаясь к переменной х, получаем уравнения и , последнее не имеет корней, т.к. арифметический квадратный корень – неотрицательное число, а первое уравнение можно решить, используя определение арифметического квадратного корня 6 2 = х 2 +11 , решение которого х=5 и х=-5.

Если уравнение можно свести к уравнению, содержащему два или несколько одинаковых выражений, то это уравнение можно решить методом замены переменной. Для этого заменяют такое выражение другой переменной, получают новое уравнение относительно новой переменной, решают его, затем осуществляют обратную замену, возвращаясь к прежней переменной.

Структурная схема программы: а) способ группировки разложение на множители

Блок-схема программы: а) способ группировки разложение на множители

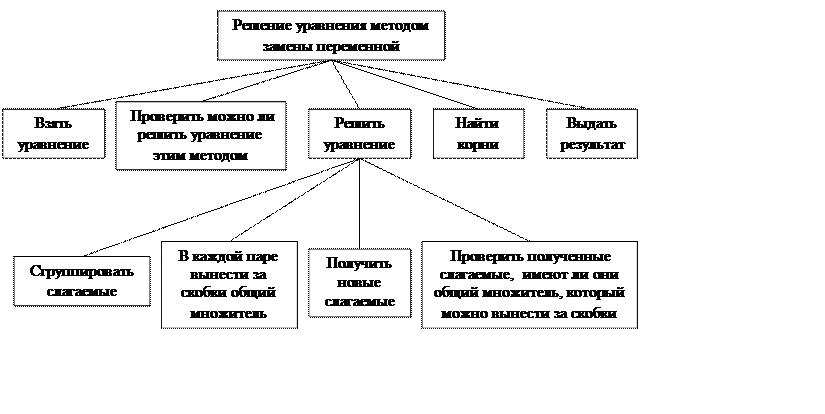
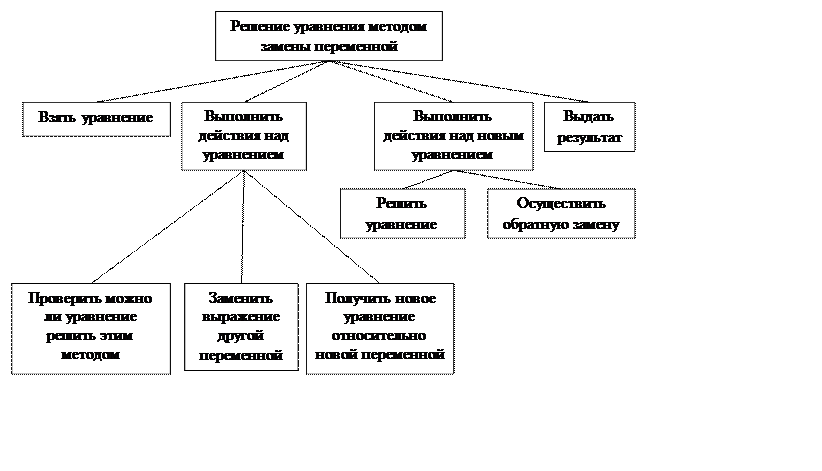
Структурная схема программы: б) замены переменной

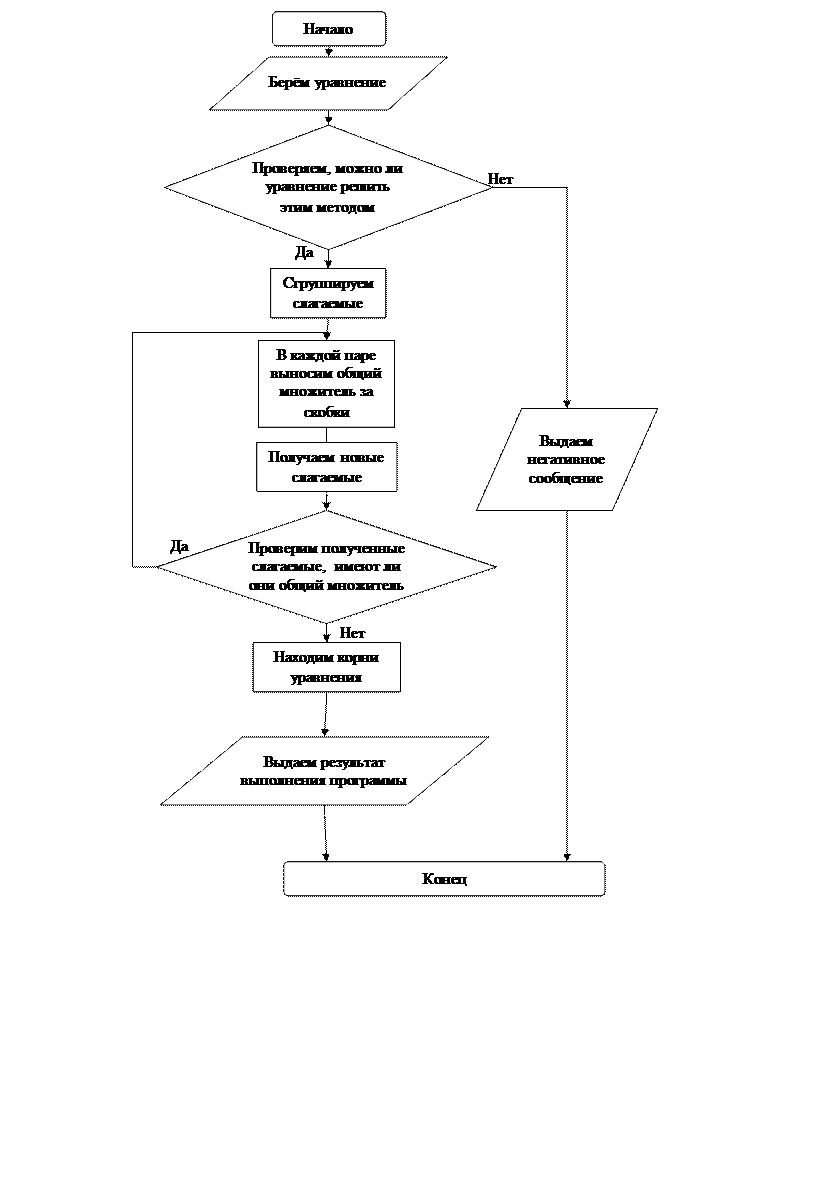
Блок-схема программы: б) замены переменной

Видео:Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать

Разложение многочлена способом группировки

О чем эта статья:

Видео:7 класс, 29 урок, Способ группировкиСкачать

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

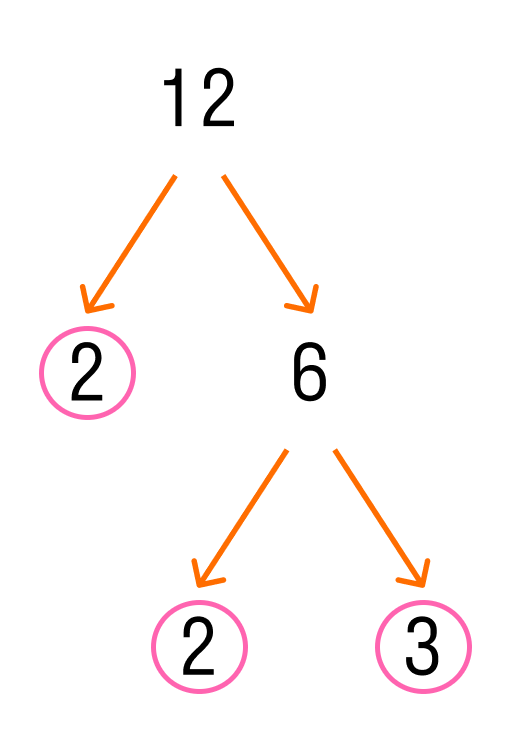
Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые обведены в кружок на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

5 способов разложения многочлена на множители

Вынесение общего множителя за скобки.
Формулы сокращенного умножения.
Метод группировки.
Выделение полного квадрата.
Разложение квадратного трехчлена на множители.

Видео:Алгебра 9 класс. 12 сентября. решение уравнения методом группировки по парамСкачать

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.
Вынести общий множитель за скобки.
Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И не всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.

up — bp + ud — bd = (up — bp) + (ud — bd)

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Получим: p(u — b) + d(u — b).

Заметим, что общий множитель (u — b).

Вынесем его за скобки:

Группировка множителей выполнена.

up — bp + ud — bd = (up + ud) — (bp + bd)

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Получим: u(p + d) — b(p + d).

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест множителей произведение не меняется, поэтому оба ответа верны:

(u — b)(p + d) = (p + d)(u — b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).

Найдем общий множитель: (m — n)
Вынесем общий множитель за скобки: (m — n)(c + d).

Ответ: c(m — n) + d(m — n) = (m — n)(c + d).

Пример 3. Разложить на множители с помощью группировки: 5x — 12z (x — y) — 5y.

5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)

Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax 2 — bx 2 + bx — ax + a — b.

Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax 2 — bx 2 + bx — ax + a — b = (ax 2 — bx 2 ) + (bx — ax) + (a — b) = x 2 (a — b) — x(a — b) + (a — b)

Получили три слагаемых, в каждом из которых есть общий множитель (a — b).

Теперь вынесем за скобку (a — b), используя распределительный закон умножения:

x 2 (a — b) + x(b — a) + (a — b) = (a — b)(x 2 + x + 1)

Ответ: ax 2 — bx 2 + bx — ax + a — b = (a — b)(x 2 + x + 1)

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Видео:Утренний разворот. Кузнецов, Венедиктов*. Курников и Баблоян / 26.01.24Скачать

Разложение способом группировки

Способ группировки — это способ разложения многочлена на множители, применяемый в тех случаях, когда члены многочлена не имеют общего множителя. Разложение способом группировки проходит в три этапа:

Группируем с помощью скобок члены многочлена, имеющие общий множитель.
Выносим общий множитель каждой группы за скобки.
Выносим за скобки общий множитель всех получившихся произведений. В данном случае общий множитель будет многочленом.

Его члены не имеют общего множителя, но мы можем сгруппировать их так, чтобы в каждой отдельной группе был общий множитель, который можно будет вынести за скобки:

Каждое получившееся произведение имеет общий множитель x + a, который теперь тоже можно вынести за скобки:

Заметим, что можно сгруппировать слагаемые иначе:

В обоих случаях группировки мы пришли к тому, что в нашем выражении появился общий многочленный множитель, который можно вынести за скобки:

Обратите внимание, что разница в начальной группировке членов не повлияла на результат разложения многочлена на множители.

Видео:Метод группировкиСкачать