Решение уравнений методом гаусса с выбором главного элемента онлайн (5 видео)

Содержание

Онлайн калькулятор. Решение систем линейных уравнений методом Гаусса
Решить систему линейных уравнений методом Гаусса
Ввод данных в калькулятор для решения систем линейных уравнений методом Гаусса
Дополнительные возможности калькулятора для решения систем линейных уравнений методом Гаусса
Метод Гаусса онлайн
Предупреждение
Метод Гаусса
Примеры решения системы линейных уравнений методом Гаусса
Решение СЛАУ методом Гаусса
📸 Видео

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Онлайн калькулятор. Решение систем линейных уравнений методом Гаусса

Используя этот онлайн калькулятор для решения систем линейных уравнений (СЛУ) методом Гаусса, вы сможете очень просто и быстро найти решение системы.

Воспользовавшись онлайн калькулятором для решения систем линейных уравнений методом Гаусса, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на решения систем линейных уравнений, а также закрепить пройденный материал.

Видео:Решение системы уравнений методом ГауссаСкачать

Решить систему линейных уравнений методом Гаусса

Изменить названия переменных в системе

Заполните систему линейных уравнений:

Видео:Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

Ввод данных в калькулятор для решения систем линейных уравнений методом Гаусса

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Для изменения в уравнении знаков с «+» на «-» вводите отрицательные числа.
Если в уравнение отсутствует какая-то переменная, то в соответствующем поле ввода калькулятора введите ноль.
Если в уравнение перед переменной отсутствуют числа, то в соответствующем поле ввода калькулятора введите единицу.

Например, линейное уравнение x ₁ — 7 x ₂ — x ₄ = 2

будет вводится в калькулятор следующим образом:

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Дополнительные возможности калькулятора для решения систем линейных уравнений методом Гаусса

Между полями для ввода можно перемещаться нажимая клавиши «влево», «вправо», «вверх» и «вниз» на клавиатуре.
Вместо x ₁, x ₂, . вы можете ввести свои названия переменных.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Решение системы уравнений методом Гаусса 4x4Скачать

Метод Гаусса онлайн

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

перемена местами двух уравнений в системе,
умножение какого-либо уравнения в системе на ненулевое действительное число,
прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Рассмотрим систему линейных уравнений:

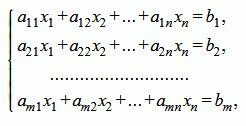Решение уравнений методом гаусса с выбором главного элемента онлайн

(1)

Запишем систему (1) в матричном виде:

Ax=b

(2)

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

(4)

Предположим a₁₁≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a₁₁. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a₂₁/a₁₁, −a₃₁/a₁₁, . −a_m1/a₁₁, соответственно. Тогда (4) примет следующий вид:

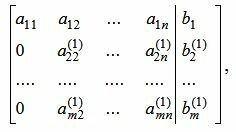(5)

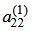
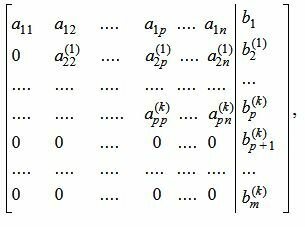На следующем этапе обнуляем все элементы столбца 2, ниже элемента . Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a₂₂. Для этого сложим строки 3, . m со строкой 2, умноженной на −a₃₂/a₂₂, . −a_m2/a₂₂, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:

(6)

Обратим внимание на последние строки. Если 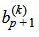. равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

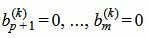
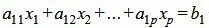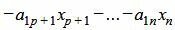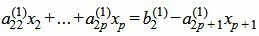Пусть . Тогда

(7)

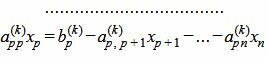Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x_p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x_p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

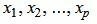
Видео:Решение системы уравнений методом Крамера 2x2Скачать

Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, запишем расширенную матрицу:

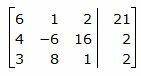Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:

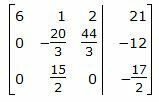Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Из вышеизложенной таблицы можно записать:

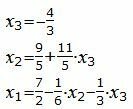Подставив верхние выражения в нижние, получим решение.

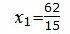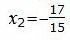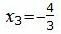Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:

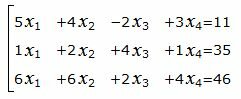Матричный вид записи: Ax=b, где

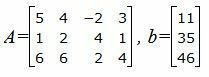Для решения системы, построим расширенную матрицу:

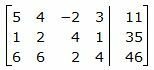Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:

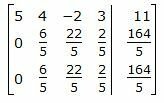Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на -1:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

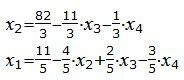где x₃, x₄− произвольные действительные числа.

Подставив верхние выражения в нижние, получим решение.

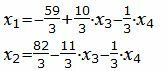где x₃, x₄− произвольные действительные числа.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

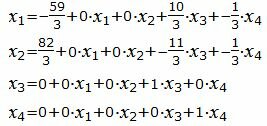Тогда векторное решение можно представить так:

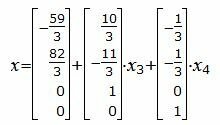где x₃, x₄− произвольные действительные числа.

Видео:VB.net Vs С++. СЛАУ Метод ГауссаСкачать

Решение СЛАУ методом Гаусса

Смысл метода: последовательно исключаем переменную за переменной, пока в одной из строк не будет однозначно определена переменная x_i. Идею можно проиллюстрировать на простом примере:
x₁ — x₂ = 3
-x₁ + 2x₂ = 1
=========== (складываем строки)
-x₂ + 2x₂= 3 + 1 = 4 или x₂ = 4
Откуда, x₁ = 7

Суть метода можно понять, проанализировав пример решения.

Решение.
Запишем систему в виде расширенной матрицы:

2	-1	0
-1	1	4
1	2	3

Далее умножаем 2-ую строку на (2) и добавляем к первой:

0	1	8
-1	1	4
1	2	3

Добавим 3-ую строку к 2-ой:

0	1	8
0	3	7
1	2	3

Умножим первую строчку на (3), 2-ую строку умножаем на (-1). Следующее действие: складываем первую и вторую строки:

0	0	17
0	3	7
1	2	3

Теперь исходную систему можно записать как:
x₃ = 51/17
x₂ = [27 — 7x₃]/3
x₁ = [14 — (2x₂ + 3x₃)]
Из 1-ой строки выражаем x₃ : 51/17 = 3
Из 2-ой строки выражаем x₂ : (27 — 7*3)/3 = 2
Из 3-ой строки выражаем x₁ : (14 — 2*2 — 3*3) = 1

Вывод: метод Гаусса является достаточно простым методом при небольшом количестве переменных и позволяет найти точное значение переменных. Процесс отыскания переменных можно упростить, если каждый раз сортировать столбцы по возрастанию.