Решение уравнений методом гаусса mpi

Постановка задачи

Необходимо реализовать параллельную программу, которая решает системы линейных алгебраических уравнений (СЛАУ) методом Гаусса средствами MPI и OpenMP. Также нужно провести теоретический анализ эффективности алгоритма, провести эксперименты и сделать выводы.

Описание последовательного алгоритма

Линейное уравнение с n неизвестными x₀, x₁, …, x_n-1 может быть определено при помощи выражения a₀x₀ + a₁x₁ + . + a_n-1x_n-1 = b где величины a₀, a₁, …, a_n-1 и b представляют собой постоянные значения.

Множество n линейных уравнений

называется системой линейных уравнений или линейной системой. В матричном виде система может представлена как Ax = b где A = (a_i,j) есть вещественная матрица размера n×n, а вектора b и x состоят из n элементов.

Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b обычно понимается нахождение значения вектора неизвестных x, при котором выполняются все уравнения системы.

Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решение рассматриваемой системы (эквивалентные преобразования). К ним относятся:

• Умножение любого из уравнений на ненулевую константу,
• Перестановка уравнений,
• Прибавление к уравнению любого другого уравнения системы.

Метод Гаусса включает последовательное выполнение двух этапов.Первый этап – прямой ход метода Гаусса – исходная система линейный уравнений приводится к верхнему треугольному виду Ux = c где матрица коэффициентов получаемой системы имеет вид

Прямой ход метода Гаусса состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений. На итерации i, 0 ≤ i 3 ).

Обратный ход алгоритма Гаусса

После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной x_n-1, после этого из предпоследнего уравнения становится возможным определение переменной x_n-2 и тд. В общем виде, выполняемые вычисления при обратном ходе метода Гаусса могут быть представлены при помощи соотношений:

Вычислительная сложность обратного хода алгоритма Гаусса составляет O(n 2 ).

Описание параллельного алгоритма. Выделение информационных зависимостей

Все вычисления методом Гаусса сводятся к однотипным вычислительным операциям над строками матрицы коэффициентов системы линейных уравнений. Значит в основу параллельной реализации алгоритма Гаусса может быть положен принцип распараллеливания по данным. Поэтому, в качестве базовой подзадачи можно принять все вычисления, связанные с обработкой одной строки матрицы A и соответствующего элемента вектора b.

При выполнении прямого хода метода Гаусса необходимо осуществить (n-1) итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду.

Выполнение итерации i, 0 ≤ i i, должны обменяться своими элементами при исключаемой переменной x_i. После сбора всех необходимых данных в каждой подзадаче может быть определено, какая из подзадач содержит ведущую строку и какое значение является ведущим элементом.

Далее для продолжения вычислений ведущая подзадача должна разослать свою строку матрицы A и соответствующий элемент вектора b всем остальным подзадачам с номерами k, k > i. Получив ведущую строку, подзадачи выполняют вычитание строк, обеспечивая тем самым исключение соответствующей неизвестной x_i.

При выполнении обратного хода метода Гаусса подзадачи выполняют необходимые вычисления для нахождения значения неизвестных. Как только какая-либо подзадача i, 0 ≤ i

Масштабирование и распределение подзадач по процессорам

Выделенные базовые подзадачи характеризуются одинаковой вычислительной трудоемкостью и сбалансированным объемом передаваемых данных. В случае, когда размер матрицы, описывающей систему линейных уравнений, оказывается большим, чем число доступных процессоров (p

Анализ эффективности

Пусть n есть порядок решаемой системы линейных уравнений, а p, p 3 /3 + n 2

Определим сложность параллельного варианта метода Гаусса. При выполнении прямого хода алгоритма на каждой итерации для выбора ведущей строки каждый процессор должен осуществить выбор максимального значения в столбце с исключаемой неизвестной в пределах своей полосы. Начальный размер полос на процессорах равен n/p, но по мере исключения неизвестных количество строк в полосах для обработки постепенно сокращается. Текущий размер полос приближенно можно оценить как (n-i)/p, где i, 0 ≤ i 3 /3)/p, тем самым, балансировка вычислительной нагрузки между процессорами в целом является достаточно равномерной. При выполнении прямого хода на каждой итерации для определения ведущей строки процессоры обмениваются локально найденными максимальными значениями в столбце с исключаемой переменной. Выполнение данного действия одновременно с определением среди собираемых величин наибольшего значения может быть обеспечено при помощи операции обобщенной редукции (функция MPI_Allreduce библиотеки MPI). Всего для выполнения такой операции требуется log₂p шагов, что с учетом количества итераций позволяет оценить время, необходимое для проведения операций редукции, при помощи следующего выражения:

где, α – латентность сети передачи данных, β – пропускная способность сети, w – размер пересылаемого элемента данных.

На каждой итерации прямого хода метода Гаусса выполняется рассылка выбранной ведущей строки. Сложность данной операции передачи данных равна:

При выполнении обратного хода алгоритма Гаусса на каждой итерации осуществляется рассылка между всеми процессорами вычисленного значения очередной неизвестной. Общее время, необходимое для выполнения подобных действий, можно оценить как:

Подводя итог, с учетом всех полученных выражений, трудоемкость параллельного варианта метода Гаусса составляет:

где τ есть время выполнения базовой вычислительной операции.

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Реализация метода Гаусса. Решения СЛАУ в системе MPI

Страницы работы

Содержание работы

по курсу «Основы параллельного программирования»

Тема: «Метод Гаусса»

Студенты: Терещенко Т., Вамбуева Т., Че Т.

Преподаватель: Медведев М.Ю.

1.Цель работы

Реализовать метод Гаусса решения СЛАУ в системе MPI двумя способами. Первый заключается в том, что соседние строки матрицы хранятся не далее, чем в соседних компьютерах. Например:

Номер строки Номер компьютера

Второй заключается в том, что принадлежность строк процессорам меняется с каждой строкой:

Номер строки Номер компьютера

2.Реализация

Программа 1 имеет следующий алгоритм работы:

• Нулевой процессор:
• Считывание и пересылка размерности матрицы, расчёт распределения строк по процессорам и пересылка этой информации.
• Считывание своей части матрицы
• Считывание остальной части матрицы и пересылка соответствующим процессорам
• Ненулевые процессоры:
• Получить размерность от нулевого компьютера и распределение строк по процессорам.
• Получить свои строки матрицы от нулевого процессора.
• Для каждого процессора:
• Для каждой строки i процессора:
  • Получить все строки с меньшими номерами, обработать их, занулив соответствующую компоненту (с номером i).
  • Переслать строку i всем процессорам, с номером, большим, чем rank.
  • Обработать свои ниже стоящие строки, занулив в них i-ю компоненту.
• Получить строку с вектором – результатом от компьютера с номером, большим, чем rank.
• Для каждой строки i процессора:
  • Вычислить i-ю компоненту вектора результата
• Переслать вектор-результат компьютерам с ранком, меньшим, чем rank
• Нулевой процессор замеряет время и пишет результат в файл.

В программе 2 использовались следующие соотношения:

Глобальный номер строки i процессора с ранком rank: rank+1+(i-1)*size

Строка с номером str находится у процессора (str-1)%size

Программа 2 имеет следующий алгоритм работы:

• Нулевой процессор:
• Считывание и пересылка размерности матрицы, расчёт числа строк в каждом процессоре и пересылка этой информации.
• Для каждой строки
  • Если это своя строка, то считать и записать в свою матрицу
  • Иначе считать и переслать соответствующему процессору.
• Ненулевые процессоры:
• Получить размерность от нулевого компьютера и число строк в каждом процессоре.
• Получить свои строки матрицы от нулевого процессора.
• Для каждого процессора:
• Для каждой строки i процессора:
  • Получить все строки с меньшими номерами, обработать их, занулив соответствующую компоненту (с номером i).
  • Переслать строку i всем процессорам, с номером, большим, чем rank.
  • Обработать свои ниже стоящие строки, занулив в них i-ю компоненту.
• Для каждой строки i процессора:
  • Получить строку с вектором – результатом от компьютера, содержащего следующую строку (i+1).
  • Вычислить i-ю компоненту результата
  • Переслать строку – результат процессору, содержащему строку (i-1)
• Нулевой процессор замеряет время и пишет результат в файл.

Очевидно, что данная реализация также работает на любом числе процессоров. В каждой реализации учтено следующее: если обнуляемый элемент – уже нуль, то никаких преобразований с данной строкой не происходит.

В случае вырожденной матрицы выдаётся соответствующее сообщение.

Видео:Решение системы уравнений методом ГауссаСкачать

Распараллеливание программы решения систем линейных алгебраических уравнений методом Гаусса с помощью OpenMP и MPI

Распараллеливание программ с помощью OpenMP

Параллельная OpenMP- программа состоит из последовательных и параллельных секций. Границы параллельных секций обозначаются директивами OpenMP. Процесс разработки OpenMP-программы включает следующие этапы:

• Разработка последовательной программы.
• Выявление участков потенциального параллелизма. Чаще всего это циклы.
• Анализ трудоемкости параллельных секций (профилирование программы). Наибольший выигрыш в производительности дает распараллеливание секций, на которые приходятся наибольшие затраты процессорного времени.
• Пошаговое распараллеливание программы, начиная с наиболее трудоемких секций.

Профилирование может производиться как с помощью специальных программных инструментов, так и простыми средствами, например, с помощью вызова специальных подпрограмм-таймеров, размещенных в различных местах программы.

Цикл эффективно распараллеливается, если отсутствуют перекрестные зависимости между его итерациями. Избавиться от таких зависимостей иногда можно, выполнив преобразование цикла .

Необходимо правильно определить область видимости переменных в параллельных секциях программы. Параметр цикла , например, должен быть объявлен локальной переменной. Инвариант цикла (величина, не изменяющаяся при выполнении итераций цикла ) должен быть глобальным.

При вычислении суммы, например, к переменной, которая используется для «накопления» суммы, должна быть применена операция приведения (редукции).

Следует обратить внимание на синхронизацию вычислений. По умолчанию в циклах используется барьерная синхронизация. Наличие синхронизаций увеличивает предсказуемость поведения программы, но замедляет ее работу.

Дополнительный выигрыш в производительности дает объединение нескольких параллельных секций в одну. В этом случае уменьшаются накладные расходы на запуск нитей и их завершение.

Трансляция OpenMP-программ

Трансляция OpenMP-программы выполняется со специальным ключом. В операционной системе Linux транслятор Intel®Compiler использует ключ –openmp , например:

#ifort –o my_prog prog_source.f90 -openmp

В операционной системе Microsoft®Windows командная строка выглядит следующим образом:

#ifort prog_source.f90 /Qopenmp

Решение систем линейных алгебраических уравнений методом Гаусса

Классическим численным методом решения систем линейных алгебраических уравнений:

где 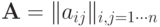— квадратная матрица коэффициентов, x — вектор неизвестных, а

b — вектор правой части, является метод Гаусса . Он относится к числу «точных» методов, то есть погрешность метода Гаусса определяется только погрешностью машинной арифметики. «Точные» методы решения систем линейных алгебраических уравнений основаны, как правило, на преобразовании исходной задачи к такой эквивалентной (имеющей то же решение), которая допускала бы простое вычисление компонентов вектора неизвестных. Это может быть система с диагональной или, как в методе Гаусса, треугольной матрицей коэффициентов. Переход к системе с верхней треугольной матрицей производится путем линейного комбинирования строк. Решение системы при этом не изменяется.

Приведем описание алгоритма для метода Гаусса.

Прямой ход

1. Найти наибольший по абсолютной величине элемент первого столбца и поменять соответствующую строку местами с первой.
2. Выбирая подходящим образом множители для элементов первой строки и складывая полученные произведения с элементами строк со 2-й по n-ю, обратить в ноль все элементы первого столбца, находящиеся ниже главной диагонали. При вычислении комбинаций следует учитывать и вектор правой части.
3. Повторить данную процедуру для второй строки и второго столбца и т. д.

Обратный ход (обратная подстановка)

1. Вычислить .
2. Для i=n-1. 1 вычислить .

Очевидным условием применимости метода Гаусса в его простейшей формулировке, приведенной выше, является отсутствие нулевых элементов на главной диагонали матрицы коэффициентов, в противном случае возникает опасность аварийного завершения программы при делении на ноль. По этой причине в реальных расчетах используются более сложные модификации метода Гаусса.

Лабораторная работа

В заданиях лабораторной работы 2.1 предлагается выполнить распараллеливание последовательной программы, предназначенной для решения систем линейных алгебраических уравнений. В задании 4 распараллеливание производится с помощью MPICH 1.2.7. Цель работы – получить навык анализа программ, выявления в них участков потенциального параллелизма с наибольшей трудоемкостью, применить для распараллеливания OpenMP и MPI , сравнить трудоемкость обоих подходов и эффективность полученного результата. Звездочкой отмечено задание повышенной сложности.

Необходимый для выполнения данной лабораторной работы справочный материал можно найти на стр. 13 – 24 методического пособия «Средства программирования для многопроцессорных вычислительных систем».

Задания для практической работы

Задание 1

Получить у преподавателя файл с исходным текстом программы (пример 1) и ознакомиться с реализацией простого метода Гаусса.

Задание 2

Откомпилировать программу, выполнить расчет. Определить процессорное время, потраченное на выполнение расчета.

Задание 3

Проанализировать последовательный код. Выявить участки потенциального параллелизма с наибольшей трудоемкостью. Для этого следует подсчитать количество операций для прямого хода метода Гаусса и хода обратной подстановки. Выполнить распараллеливание с помощью OpenMP. Определить процессорное время, потраченное на выполнение расчета для разного числа потоков (меньшего, равного и большего, чем число процессоров). Сравнить с результатом, полученным в задании 2. Объяснить полученный результат.

Задание 4*

Распараллелить программу с помощью MPI. Определить процессорное время, потраченное на выполнение расчета. Сравнить с результатами, полученными в заданиях 2 и 3.

Задание 5

На основании результатов, полученных при выполнении заданий данной лабораторной работы, написать отчет, в котором содержатся выводы об эффективности различных способов распараллеливания исходного последовательного кода и трудоемкости реализации этих способов на практике.

Пример 1

В программе на языке Fortran 90 реализован простой метод Гаусса без выбора ведущего элемента.

🔍 Видео

Решение системы уравнений методом Гаусса 4x4Скачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

Метод Гаусса решения систем линейных уравненийСкачать

Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

МЕТОД ГАУССА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

решение системы уравнений методом ГауссаСкачать

Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать

12. Решение систем линейных уравнений методом ГауссаСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Метод Гаусса и метод Жордана-ГауссаСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Метод Гаусса Пример РешенияСкачать

Линейная алгебра, 9 урок, Метод ГауссаСкачать

Метод Гаусса решения систем линейных уравненийСкачать
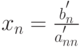