Построение решений обыкновенных дифференциальных уравнений
Решение дифференциального уравнения 1-го порядка


Простой метод Эйлера реализуется применением на каждом шаге вычислений следующих итерационных выражений:
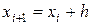
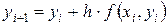
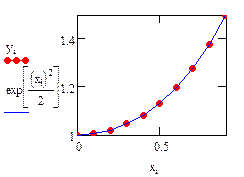
Рассмотрим реализацию метода в MathCADна примере уравнения:
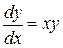
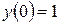
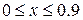
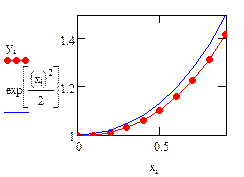
Аналитическое решение известно и имеет вид:

Краткие сведения о составлении программ в MathCAD
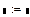
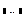
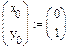
Графиквставляется командой Insert→ Graph→ X-YPlotили клавишей «@».
Для удобства в работе рекомендуется отключить автоматическое вычисление, убрав галочку с опции меню Tools→ Calculate→ AutomaticCalculation. Тогда расчет не будет выполняться в ходе набора программы, а запуститься только после нажатия кнопки Calculate, расположенной на панели инструментов (в виде значка 
Ниже приведена расчетная программа. Повторите её. Получите графики с тем же форматом линий. Формат линий графика можно изменить, открыв с помощью ПК мыши контекстное меню и выбрав Format… → Traces.
Программа для простого метода Эйлера
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
 |
| Задание цикла |
 |
| Задание начальных условий |
 |
| Итерационные уравнения |
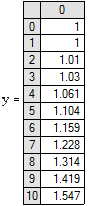
| Результаты решения: |
 |
 |
 |
 |
Следующая программа реализует модифицированный метод Эйлера. Отличие от простого метода заключается в итерационных уравнениях.
Программа для модифицированного метода Эйлера
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
 |
| Задание цикла |
 |
| Задание начальных условий |
| Итерационные уравнения |
 |
| Результаты решения: |
 |
 |
 |
 |
Метод Рунге-Кутта 4-го порядка используется в тех случаях, когда необходима высокая точность расчетов, недостигаемая методами Эйлера.
Программа для метода Рунге-Кутта
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
| Задание коэффициентов k1, k2, k3, k4 как функций пользователя: |
 |
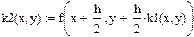 |
 |
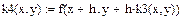 |
 |
| Усредненная функция |
 |
| Задание цикла |
 |
| Задание начальных условий |
 |
| Итерационные уравнения |
| Результаты решения: |
 |
 |
 |
 |
Решение дифференциальных уравнений 2-го порядкаметодом Рунге-Кутта.
Подход к реализации метода основан на использовании дополнительной функции 


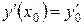
Преобразуем задачу к системе из двух уравнений:


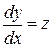

Тогда получим следующее обобщение итерационной схемы:



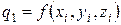
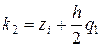




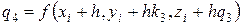
Отметим, что значения на каждом следующем шаге рассчитываются по значениям, полученным на предыдущем. Кроме того, использованы прежние правила «взвешивания» коэффициентов при усреднении.
Пример математической модели с дифференциальным уравнением 2-го порядка
Рассмотрим уравнение колебательного процесса при наличии внешнего периодического воздействия:

где t– время, и искомой является зависимость 
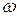
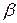
Если 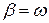

где Aи 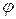
Когда 

В этом случае колебательный процесс слагается из собственных колебаний с частотой 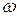
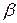
Моделирование резонансных колебаний
Методом Рунге-Кутта найдем решение задачи:

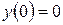


Согласно изложенной выше теории, аналитическое решение уравнения имеет вид:
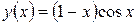
Ниже приведен алгоритм расчета и его реализация в MathCAD.
Программа расчета резонансных колебаний методом Рунге-Кутта
 |
| Шаг изменения x |
 |
| Число шагов |
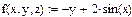 |
| Функция в системе уравнений dy/dx = z и dz/dx = f(x,y,z) |
| Задание коэффициентов как функций пользователя: |
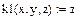 |
 |
 |
 |
 |
 |
 |
 |
| Усредненные функции: |
 |
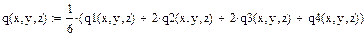 |
 |
| Задание цикла |
 |
| Задание начальных условий |
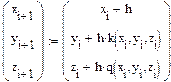 |
| Итерационные уравнения |
 |
| Результаты решения: |
Задание для самостоятельного выполнения
Найти решение уравнения вынужденных колебаний:

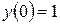
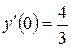
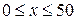
Решение представить в виде графика. Для сравнения привести и график точного решения (также как это было сделано для резонансных колебаний).
Видео:Метод ЭйлераСкачать

Тема 7. Решение дифференциальных уравнений и систем в MathCad
Краткие теоретические сведения
Для решения дифференциальных уравнений с начальными условиями система Mathcad имеет ряд встроенных функций:
rkfixed – функция для решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;
Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;
Odesolve – функция, решающая ОДУ блочным методом.
Ниже приведено описание стандартной функции rkfixed с указанием параметров функции.
y – вектор начальных условий из k элементов ( k – количество уравнений в системе);
x1 и x2 – левая и правая границы интервала, на котором ищется решение ОДУ или системы ОДУ;
p – число точек внутри интервала (x1, x2), в которых ищется решение;
D – вектор, состоящий из k-элементов, который содержит первую производную искомой функции или первые производные искомых функций, если речь идет о решении системы.
Результатом работы функции является матрица из p +1 строк, первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – сами решения.
На рисунке 2.7.1 приведены конкретные примеры решения различных дифференциальных уравнений и систем ОДУ в MathCAD .
Рисунок 2.7.1 – Примеры решения дифференциальных уравнений и систем
При решении дифференциального уравнения первого порядка нужно создать вектор начальных условий из одного элемента Y 1 , который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции rkfixed указывается имя вектора Y , границы интервала, на котором ищется решение уравнения, например, (0 ; 2), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D . В результате получается матрица z , в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой результирующей функции. При построении графика функции первый столбец полученной матрицы указывается как аргумент, второй столбец – как функция.
При решении системы дифференциальных уравнений нужно создать вектор начальных условий из двух элементов, например, вектор v , который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции rkfixed указывается имя вектора v , и границы интервала, на котором ищется решение уравнения, например, (0 ; 5), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D . В результате получается матрица s , в первом столбце которой содержатся значения аргумента искомых функций, во втором и третьем столбцах – значения самих функций при соответствующем значении аргумента. При построении графика можно воспользоваться первым столбцом полученной матрицы как аргументом, а вторым и третьим столбцами – как функциями.
На рисунке 2.7.2 приведен пример решения дифференциального уравнения второго порядка с использованием функции rkfixed . Необходимо решить дифференциальное уравнение второго порядка с заданными начальными условиями вида:
Рисунок 2.7.2 – Пример решения дифференциальных уравнений второго порядка с помощью rkfixed
Для решения уравнения с помощью функции rkfixed нужно выполнить замену переменных и привести дифференциальное уравнение второго порядка к двум дифференциальным уравнениям первого порядка. Вид этих уравнений приведен ниже.
Документ формируется точно так же, как и при решении системы ОДУ.
На рисунке 2.7.2 показана возможность вычисления вектора второй производной найденной функции – вектора а, построены графики исходной функции, функций первой и второй производных.
Практическая часть темы 7
7.1 Решение дифференциальных уравнений первого порядка
Последовательность действий для р ешения дифференциального уравнения первого порядка такова:
q сформировать вектор начальных условий из одного элемента, присвоив начальное значение искомой функции переменной с индексом, например: 

q определить вектор-функцию из одного элемента, которая содержит первую производную неизвестной функции:
· набрать имя функции с двумя параметрами: первый параметр – аргумент искомой функции (независимая переменная), второй – имя вектора, содержащего искомую функцию (можно использовать имя вектора начальных условий), например, D ( x , Y );
· набрать оператор «:=» и выражение для первой производной (выразить из дифференциального уравнения), в котором вместо имени искомой функции подставлен первый элемент вектора-параметра, например, для уравнения 


q присвоить некоторой переменной значение функции rkfixed , указав в скобках следующие параметры:
· первый – имя вектора начальных условий,
· второй – левая граница интервала, на котором ищется решение, в виде числовой константы,
· третий – правая граница интервала, на котором ищется решение, в виде числовой константы,
· четвертый – количество точек, в которых ищется решение,
· пятый – имя вектора-функции, описывающего первую производную, без параметров;
например: 
(в результате получится матрица Z , в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой функции);
q вывести матрицу, содержащую решение ДУ с помощь оператора «=», например: Z = ;
q построить график найденной функции ( см. тему 5 ), указав в качестве аргумента по оси абсцисс столбец 



Пример 7.1 Найти численное решение дифференциального уравнения первого порядка 
Выполнить графическую интерпретацию результатов.
7.2 Решение систем дифференциальных уравнений
Последовательность действий для р ешения системы дифференциальных уравнений первого порядка такова (описана для значения ORIGIN =0 ):
q перейти в исходной системе уравнений к однотипным обозначениям функций и выразить первые производные,
например, систему 

q в документе MathCad сформировать вектор начальных условий, количество элементов которого равно количеству уравнений системы, присвоив его некоторой переменной (см. тему 2);
например, 
q определить вектор-функцию, которая содержит первые производные искомых функций:
· набрать имя функции с двумя параметрами: первый параметр – аргумент искомых функций (независимая переменная), второй – имя вектора, содержащего искомые функции (можно использовать имя вектора начальных условий), например, D ( t , V );
(Замечание: если независимая переменная явно не присутствует в системе, то в качестве ее имени можно выбрать любую переменную)
· набрать оператор «:=» и вставить шаблон вектора, количество элементов которого равно количеству уравнений системы (см. тему 2)
· набрать в качестве элементов вектора правые части системы уравнений, в которых искомые функции представлены соответствующими элементами вектора-параметра, например,

q присвоить некоторой переменной значение функции rkfixed , указав в скобках следующие параметры:
· первый – имя вектора начальных условий,
· второй – левая граница интервала, на котором ищется решение, в виде числовой константы,
· третий – правая граница интервала, на котором ищется решение, в виде числовой константы,
· четвертый – количество точек, в которых ищется решение,
· пятый – имя вектора-функции, описывающего первые производные, без параметров;
например: 
(в результате получится матрица Z , в первом столбце которой содержатся значения аргумента искомых функций, во втором – значения первой функции, в третьем – значения второй функции и т. д.);
q вывести матрицу, содержащую решение системы ДУ с помощь оператора «=», например: Z = ;
q построить графики найденных функций ( см. тему 5 ), указав в качестве аргумента по оси абсцисс первый столбец матрицы решений, например, 


Пример 7.2 Найти решение системы дифференциальных уравнений
на интервале от 0 до 0.5 в 1000 точках, при следующих начальных условиях: x (0)=0.1 и y (0)=1.
Выполнить графическую интерпретацию результатов.
Видео:MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

28. Тема 7. Решение дифференциальных уравнений и систем в MathCad. Краткие теоретические сведения
Для решения дифференциальных уравнений с начальными условиями система Mathcad имеет ряд встроенных функций:
Rkfixed – функция для решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;
Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;
Odesolve – функция, решающая ОДУ блочным методом.
Ниже приведено описание стандартной функции Rkfixed с указанием параметров функции.
Y – вектор начальных условий из K элементов (k – количество уравнений в системе);
X1 и X2 – левая и правая границы интервала, на котором ищется решение ОДУ или системы ОДУ;
P – число точек внутри интервала (x1, x2), в которых ищется решение;
D – вектор, состоящий из K-Элементов, который содержит первую производную искомой функции или первые производные искомых функций, если речь идет о решении системы.
Результатом работы функции является матрица из p+1 строк, первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – сами решения.
На рисунке 2.7.1 приведены конкретные примеры решения различных дифференциальных уравнений и систем ОДУ в MathCAD.
При решении дифференциального уравнения первого порядка нужно создать вектор начальных условий из одного элемента Y1, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции Rkfixed Указывается имя вектора Y, границы интервала, на котором ищется решение уравнения, например, (0 ; 2), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D. В результате получается матрица Z, в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой результирующей функции. При построении графика функции первый столбец полученной матрицы указывается как аргумент, второй столбец – как функция.
При решении системы дифференциальных уравнений нужно создать вектор начальных условий из двух элементов, например, вектор V, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции Rkfixed Указывается имя вектора V, и границы интервала, на котором ищется решение уравнения, например, (0 ; 5), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D. В результате получается матрица S, в первом столбце которой содержатся значения аргумента искомых функций, во втором и третьем столбцах – значения самих функций при соответствующем значении аргумента. При построении графика можно воспользоваться первым столбцом полученной матрицы как аргументом, а вторым и третьим столбцами – как функциями.
На рисунке 2.7.2 приведен пример решения дифференциального уравнения второго порядка с использованием функции Rkfixed. Необходимо решить дифференциальное уравнение второго порядка с заданными начальными условиями вида:
Рисунок 2.7.2 – Пример решения дифференциальных уравнений второго порядка с помощью Rkfixed
Для решения уравнения с помощью функции Rkfixed нужно выполнить замену переменных и привести дифференциальное уравнение второго порядка к двум дифференциальным уравнениям первого порядка. Вид этих уравнений приведен ниже.
Документ формируется точно так же, как и при решении системы ОДУ.
На рисунке 2.7.2 показана возможность вычисления вектора второй производной найденной функции – вектора А, построены графики исходной функции, функций первой и второй производных.
🎥 Видео
Численное решение задачи Коши методом ЭйлераСкачать

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Mathcad-09. Пример: уравненияСкачать

Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

5 Численное решение дифференциальных уравнений Part 1Скачать

MatLab. Решение дифференциального уравнения.Скачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Решение задачи Коши в MathCADСкачать

1 Одно уравнениеСкачать

Решение СЛАУ в пакете MathCadСкачать

Работа с MathCad Prime. Решение дифференциальных уравнений.Скачать

Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Пример решения уравнения в MathCAD 14 (33/34)Скачать

Mathcad-10. Пример: дифференциальные уравненияСкачать












