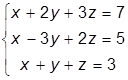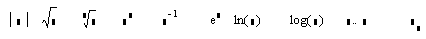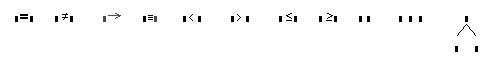- Mathcad для студентов
- Mathcad для начинающих
- Скачать программы бесплатно
- Решение системы линейных алгебраических уравнений матричным способом в Mathcad
- Решение системы линейных алгебраических уравнений методом Крамера в Mathcad
- Матрицы и векторы в Mathcad
- Матричные функции в Mathcad
- Матричные вычисления в Mathcad
- Матричные функции
- Основные операции с матрицами и векторами
- Решение системы линейных алгебраических уравнений матричным способом
- Решение системы линейных алгебраических уравнений методом Крамера
- Пример решения СЛАУ матричным методом в Mathcad
- 📺 Видео
Видео:Решение СЛАУ в пакете MathCadСкачать

Mathcad для студентов
Видео:MathCAD решение матричного уравнения 1.wmvСкачать

Mathcad для начинающих
Видео:MathCAD Решение системы линейных уравнений матричным методомСкачать
Скачать программы бесплатно
Видео:MathCAD решение матричного уравнения 3.wmvСкачать

Решение системы линейных алгебраических уравнений матричным способом в Mathcad
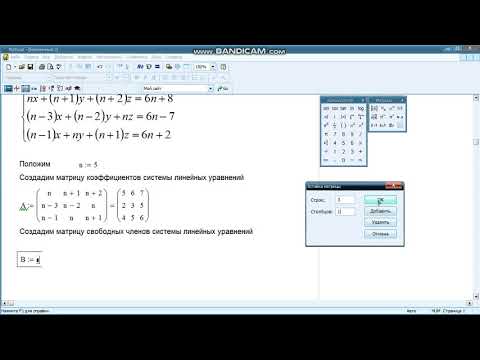
Рассмотрим системы линейных алгебраических уравнений в Mathcad в векторно-матричной форме A*x =b, где А – квадратная матрица коэффициентов при неизвестных, причем определитель матрицы должен быть отличным от нуля; х- вектор неизвестных; b — вектор свободных членов. Решение данной сводится к следующему. Если определитель матрицы А отличен от нуля, то матрица А обратима. Тогда, умножив левую и правую часть и сходного уравнения на обратную матрицу (А-1), получаем решение в виде x=A-1*b. Реализовать полученное решение средствами Mathcad не представляет сложностей. Для случая бесконечного множества решений получаем сингулярную матрицу, Mathcad выдает сообщение “Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию” и прерывает вычисления. На листинге представлен пример решения систем линейных алгебраических уравнений.
Видео:Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

Решение системы линейных алгебраических уравнений методом Крамера в Mathcad
В Mathcad метод Крамера также предназначен для решения системы n линейных уравнений с n неизвестными вида A*x =b на основе предварительного вычисления определителей системы, при условии, что определитель 


Видео:Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

Матрицы и векторы в Mathcad
Операции, выполняемые над векторами и матрицами в Mathcad, можно разбить на две большие группы. К первой группе относятся операции, которые применяются к отдельным векторам и матрицами. Например, транспонирование матрицы или вычисление обратной матрицы в Mathcad. Ко второй группе относятся операции, которые выполняются над группой векторов и матриц. Как правило, они выполняются над двумя матрицами или матрицей и вектором. Например, сложение, вычитание матриц, перемножение матриц или умножение матрицы и вектора. К векторам и матрицам в Mathcad, при выполнении операций над ними, могут предъявляться определенные требования в соответствии с требованиями классической математики. Например, при перемножении матрицы и вектора, количество столбцов матрицы должно быть равно количеству срок вектора. Поэтому при работе с векторами и матрицами пользователь должен иметь необходимую математическую подготовку. В таблице приведены основные операции, выполняемые над векторами и матрицами, используемые в Mathcad. В таблице приняты следующие обозначение: А – массив, под которым понимается вектор или матрица, М – матрица, z — скаляр, v – вектор.
Наиболее удобно выполнять матричные вычисления с использованием кнопок панели инструментов “Матрица”. По умолчанию индексация строк и столбцов элементов матрицы начинается с 0. Для того чтобы индексация начиналась с 1, необходимо системной переменной ORIGIN присвоить значение 1. На листинге приведен пример матричных вычислений в Mathсad.
Видео:MathCAD решение матричного уравнения 2Скачать

Матричные функции в Mathcad
Mathсad имеет более 50 функций, предназначенных для работы с векторами и матрицами. Все функции можно разбить на группы по их функциональному назначению. Например, функции, предназначенные для создания матриц общего и специального вида, редактирования и преобразования матриц, функции, определяющие параметры матриц и т. д. Рассмотрим часть этих функций, которые имеют наибольшее прикладное значение.
Среди функций, предназначенных для создания матриц, следует выделить функцию matrix(L,N,f), где L – число строк матрицы, N – число столбцов матрицы, f – функция f(l,n) при . Другая функция из этой группы identity(n). Функция предназначена для создания единичной матрицы размерности n. Следующая функция geninv(M) позволяет осуществить обращение матрицы M, аналогично операции M -1 .
Для определения размерности матрицы в Mathcad предназначены функция rows(M), определяющая число строк матрицы M, и функция cols(M), определяющая число колонок матрицы M.
Сортировку элементов матрицы осуществляют две функции csort(M,i), rsort(M,j). Функция csort(M,i) обеспечивает сортировку по возрастанию элементов i – го столбца путем перестановки строк, а функция rsort(M,j) – сортировку по возрастанию элементов j –ой строки путем перестановки столбцов.
Для определения минимального и максимального элемента матрицы используются функции min(M) и max(M).
Выделить произвольную подматрицу из матрицы М в Mathcad можно посредством функции submatrix (M, r1, r2, c1, c2), где М – исходная матрица, r1 и r2 –нижний и верхний номер строки матрицы М, включаемых в результирующую подматрицу, а с1 и с2 – нижней и верхний номер столбца матрицы М, включаемых в результирующую подматрицу. Слияние матриц можно осуществить, используя функции augment(A,B,…) и stack(A,B,…). Функция augment(A,B,…) предназначена для слияния матриц А, В и т.д. слева направо. Причем количество строк в матрицах должно быть одинаково. Вторая функция stack(A,B,…) выполняет слияние матриц сверху вниз. Количество столбцов в матрицах должно быть также одинаково. Данные функции могут быть применены и к векторам. На листинге приведен пример использования рассмотренных матричных функций.
Видео:Решение систем линейных уравнений в MathCAD 14 (31/34)Скачать
Матричные вычисления в Mathcad
Создание векторов и матриц реализовано в Mathсad различными способами. В данном разделе рассматриваются только функции и операции с векторами и матрицами, а так же прикладное использование векторов и матриц для решения некоторых задач.
Матричные функции
В Mathсad очень много функций, предназначенных для работы с матрицами и векторами.
Основные операции с матрицами и векторами
Операции, выполняемые над векторами и матрицами, можно разбить на разные большие группы.
Решение системы линейных алгебраических уравнений матричным способом
В Mathcad можно решать системы линейных алгебраических уравнений матричным способом.
Решение системы линейных алгебраических уравнений методом Крамера
Также предназначен метод Крамера для решения системы n линейных уравнений с n неизвестными.
Видео:Решение системы уравнений методом ГауссаСкачать

Пример решения СЛАУ матричным методом в Mathcad
Задание. Решите систему линейных алгебраических уравнений в матричном виде
Указания:
1. Установите режим автоматических вычислений.
2. Введите матрицу системы и матрицу-столбец правых частей.
3. Вычислите решение системы по формуле 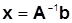
4. Проверьте правильность решения умножением матрицы системы на вектор-столбец решения.
5. Найдите решение системы с помощью функции lsolve и сравните результаты вычислений.
Фрагмент рабочего документа Mathcad, содержащий решение системы, приведен ниже.
Указание. В приведенном документе для сравнения найдено решение системы с использованием функции решения систем линейных алгебраических уравнений lsolve(A, b)
Решите матричное уравнение Ах= b (систему линейных алгебраических уравнений) из индивидуального задания к работе №3.
Лабораторная работа №6
Метод Гаусса решения системы линейных алгебраических уравнений
Метод Гаусса применяется для решения системы линейных алгебраических уравнений (6.1).
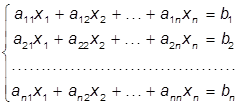
В матричной форме эта система имеет вид Ах = b, где
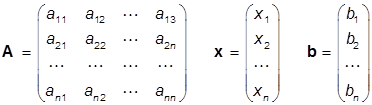
Воспользуемся тем фактом, что решение системы не изменяется при выполнении следующих операций:
а) перестановка двух уравнений местами;
б) умножение одного из уравнений на число, которое не равно нулю;
в) вычитание одного уравнения, умноженного на некоторое число, из другого.
Если a11=0, поменяем местами первое уравнение с таким j-м уравнением, что аj1 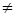
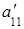
Рассмотрим полученные уравнения с номерами 2, . п. Они образуют систему из (n-1) уравнений с (n-1) неизвестными. Выполним с этой системой те же операции, что и с предыдущей (второй шаг метода Гаусса).
Следующий шаг выполним для следующих (n-2) уравнений и так далее.
Если на каждом шаге удается выбрать ведущий элемент, то после ряда преобразований система уравнений приобретает треугольный вид:
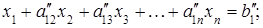 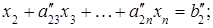 ………………………… ………………………… 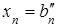 . . | (6.3) |
Из последнего уравнения можно получить значение неизвестного 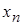
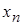
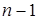
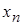
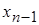
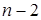
Но лучше продолжить вычисления по следующей схеме (обратный ход методу Гаусса). Отнимем последнее уравнение системы (6.3), умноженное на 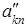
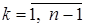
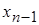
После ряда преобразований система (6.3) будет приведена к виду
Рассмотрим случай, когда на очередном шаге не удается выбрать ведущий элемент. Это произойдет в том случае, когда на следующем r-м шаге все коэффициенты при неизвестной 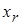
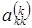
Метод Гаусса относят к классу точных (прямых) методов, но не всегда этот метод позволяет получить точное решение. На практике коэффициенты при неизвестных могут быть результатом эксперимента, поэтому являются приближенными числами. Действия над приближенными числами выполняются с округлением. В результате решение системы будет также приближенным.
Индивидуальное задание к лабораторной работе №6
Решите систему линейных алгебраических уравнений (из индивидуального задания к работе №3) методом Гаусса в среде Mathcad либо посредством программного продукта на языке программирования С..
Основные сведения по работе в среде MATHCAD
Рассмотрим внешний вид программы и основные приемы управления.
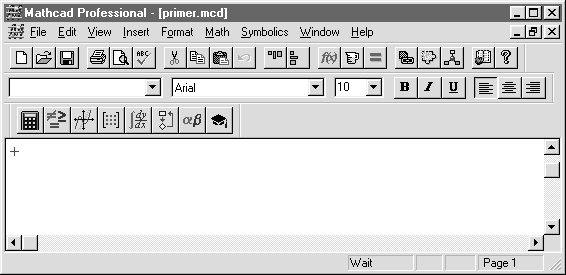


 |




Рис.1. Окно программы «Mathcad»
1 – заголовок окна;
2 – главное меню программы;
3 – панели инструментов;
4 – рабочее поле, окно редактирования;
5 – строка статуса.
Большинство вычислений в Mathcad можно выполнить тремя способами:
• выбором операции в меню;
• с помощью кнопочных панелей инструментов;
• обращением к соответствующим функциям.
Основные операции, закрепленные за пунктами меню, дублируются соответствующими кнопками панелей инструментов. Например, для обращения к встроенной функции можно вставить функцию в рабочий документ, выбрав нужное имя из списка функций, можно ввести имя функции с клавиатуры или, для наиболее часто используемых функций, вставить имя функции щелчком по кнопке в панели инструментов. Таким образом, во всех трех случаях соблюдается один и тот же порядок действий:
• выбор операции производится щелчком мыши по пункту меню или по кнопке в панели инструментов, после чего, если нужно, пользователь получает доступ к ниспадающему меню или к дополнительной панели;
когда операция выбрана, пользователь вводит необходимую информацию в окне диалога или заполняет помеченные поля в поле ввода, которое открывается непосредственно в рабочем документе.
Как уже упоминалось выше, вторая строка рабочего окна Mathcad — строка меню (см. рис. 2).
Рис.2. Работы с главным меню
Рассмотрим содержание каждого пункта меню и опишем правила выполнения наиболее часто используемых операций.
Некоторые строки ниспадающих меню содержат знак 

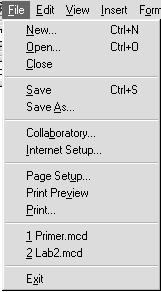 Рис. 3. Меню Файл Рис. 3. Меню Файл |
Меню File (Файл). Щелчком по слову File открывается меню операций с файлами (рис. 3). Пункты New (Новый),Open(Открыть),Close (Закрыть),Save (Сохранить),Save As (Сохранить как) предназначены соответственно для выполнения операций открытия нового рабочего документа, чтения с диска созданного ранее рабочего документа, закрытия текущего рабочего документа, сохранения рабочего документа в файле на диске в текущей папке или сохранения в файле, имя и папка которого указываются при сохранении. Все эти операции выполняются стандартным для Windows способом: указанием имен и папок в окнах диалога.
Следующие два пункта содержат операции, доступные пользователям, компьютеры которых имеют выход в Internet:Collaboratory(Сотрудничество) — присоединение через сервер MathSoft к Collaboratory, бесплатному Internet-форуму, обслуживающему всемирное сообщество пользователей Mathcad,Internet Setup — установка связи с сервером MathSoft.
ПунктыPage Setup (Параметры страницы),Print Preview(Предварительный просмотр),Print (Печать) содержат соответственно операции подготовки, просмотра и печати рабочих документов Mathcad.
Следом в открывающемся менюFile расположен список имен последних четырех документов Mathcad. Щелчком (левая кнопка мыши) по строке с именем можно вызвать на экран любой из этих документов. И последний пункт — Exit (Выход), как и у всех Windows-приложений, завершает сеанс работы с Matcad.
 Рис. 4. Меню Редатирование Рис. 4. Меню Редатирование |
Меню Edit (Редактирование). Это меню (рис. 4) содержит стандартные для Windows-приложений операции редактирования рабочего документа:Undo (Отменить последнюю операцию), Redo (Отменить последнюю операцию Undo),Cut (Вырезать), Copy (Копировать), Paste (Вставить), Paste Special (Специальная вставка), Delete (Удалить), Select All (Выделить все), Find (Найти), Replace (Заменить). Go to Page (Перейти к странице),Check Spelling (Проверка орфографии), Links(Связывание), Объект (Для MathConnex и OLE).
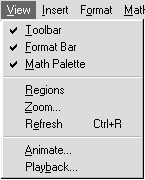 Рис. 5. Меню Просмотр Рис. 5. Меню Просмотр |
Меню View (Просмотр). Это меню (рис. 5) содержит операции настройки окна Mathcad. Если строка менюToolbar(Панель инструментов),Format Bar (Панель форматирования) илиMath Palette(Панель математических инструментов) помечена символом Ö, то на экране размещается соответствующая панель инструментов. ПунктыRegions (Области),Zoom (Микроскоп),Refresh (Перерисовывание) содержат операции преобразования изображения в рабочем документе.Animate (Анимация) иPlayback (Воспроизвести, Проиграть) — операции построения и запуска анимаций.
Меню Insert (Вставить). В этом меню (рис. 6) пунктGraph (График) открывает доступ к семи операциям построения различных типов графиков, которые собраны в дополнительное меню графиков.
После щелчка по строке дополнительного меню (см. рис. 7) в рабочем документе открывается поле построения:
• X-Y Plot. — графика функции одной переменной в декартовых координатах;
• Polar Plot — графика функции одной переменной в полярных координатах;
• Surface Plot — графика функции двух переменных в декартовых координатах — поверхности;
• Contour Plot — контурных линий (линий уровня функции двух переменных) в декартовых координатах;
• 3D Scatter Plot — изображения точек в трехмерном пространстве, заданных декартовыми координатами;
• 3D Bar Chart 3b — трехмерной гистограммы;
• Vector Field Plot — векторного поля.
Рис. 6. Меню ВставкаРис. 7. Меню График;
Порядок действий при построении всех графиков одинаков. После щелчка мышью по строке меню в рабочем документе открывается поле построения графика с помеченными для ввода позициями, которые нужно заполнить для определения графика. Когда график определен (т.е. заполнены все помеченные позиции), для его построения нужно щелкнуть по строкеCalculate (Вычислить) в меню Math, нажать на клавиатуре клавишу или щелкнуть в панели Toolbar по кнопке. При автоматическом режиме вычислений график будет построен после щелчка мышью вне поля графика.
Mathcad предоставляет пользователю разнообразные средства форматирования графика — изменение толщины и цвета линии, вида осей координат, координатные сетки, текстовые комментарии и др. Для того чтобы изменить вид изображения, нужно щелкнуть дважды по полю графика и установить требуемые параметры в окнах настройки. Научиться форматировать графики лучше всего экспериментально: постройте график, затем щелкните дважды по полю графика, определите параметр в окне настройки, щелкните по кнопке Применить и проанализируйте изменение на графике. Используйте кнопку контекстной подсказки Справка в окне настройки параметров. Правила ввода и форматирования графиков подробно описаны в соответствующих разделах встроенного справочника.
Щелчок поMatrix (Матрица) открывает в рабочем документе окно определения размерности матрицы (число строк, число столбцов). После тогокак размерность матрицы определена, в рабочем документе открывается поле ввода матрицы с помеченными позициями для ввода элементов.
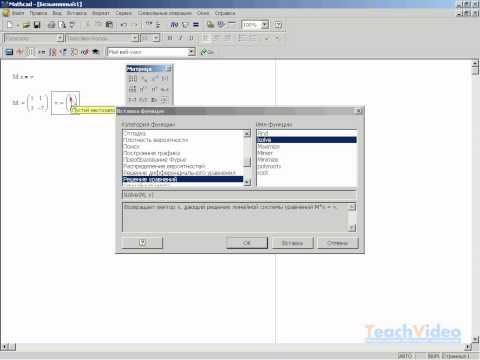
Щелчок поFunction (Функция) открывает окно диалога списка встроенных функций Mathcad. При этом для того чтобы вставить функцию в рабочий документ, нужно выбрать в окне с помощью стрелок прокрутки нужную функцию из списка* функций, щелкнуть по кнопке Insert и ввести в помеченных позициях аргументы (аргумент) функции.
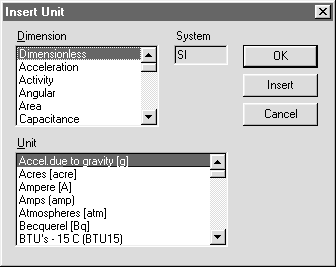 Рис. 8. Окно выбора единиц измерения Рис. 8. Окно выбора единиц измерения |
Щелчок поUnit (Единица) открывает окно списка определенных в Mathcad единиц измерения (рис. 8). В окне System (Система) следует ввести используемую систему единиц (SI, CGS, US или MKS), в окнеDimension (Размерность) — выбрать стрелками прокрутки соответствующую размерность, а в окнеUnit (Единица) — нужную единицу измерения. После щелчка по кнопке Insert соответствующее наименование будет вставлено в рабочий документ, а окно выбора единицы останется открытым; после щелчка по кнопке OK будет вставлено наименование единицы измерения и окно закроется.
ПунктPicture (Рисунок) задает операцию вставки рисунка. Пункт Text Region (Область текста) используется для определения поля текстовых комментариев; щелчком по строке Math Region (Математическая область) в текстовый комментарий вставляется поле ввода математических символов; щелчком по строкеPage Break (Разрыв страницы) в рабочий документ вставляется признак конца страницы.
ОперацииHiperlink, Reference, Component и Object предназначены для создания достаточно сложных конструкций: Hiperlink содержит набор операций для создания гипертекстовых ссылок; Reference — операция создания перекрестных ссылок для документов, Mathcad; Component и Object — операции внедрения компонент и объектов из других приложений.
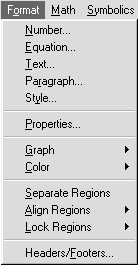 Рис. 9. Меню форматирования Рис. 9. Меню форматирования |
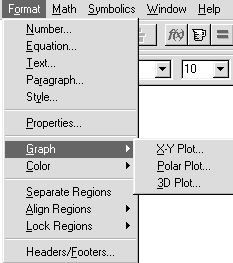
Меню Format (Формат). Все операции этого меню (рис. 9) предназначены для определения стиля и формы отображения выражений, данных, результатов вычислений и графиков в рабочем документе — определения цветов фона и надписей, размера и типа шрифта, выравнивания текстов в рабочем документе, разделения рабочего документа на области и др. При установке Mathcad по умолчанию выбран некоторый нейтральный стиль оформления. Если пользователь хочет разнообразить оформление, он может ознакомиться с возможностями меню Format в справочнике, руководстве пользователя или «экспериментально». Ниже рассматриваются только пункты Number (Число) иGraph (График), которые часто используются при решении математических задач.
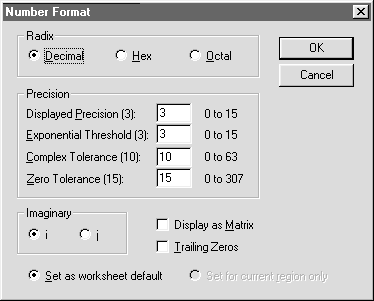 Рис. 10. Окно настройки отображения чисел Рис. 10. Окно настройки отображения чисел |
Пункт Number (Число) содержит операции определения форматов вывода числовых данных и результатов. Щелчок по Number открывает диалоговое окно ввода параметров (рис. 10).
В полеRadix (Основание системы счисления* помечается выбранная система счисления (на рис. 10 — десятичная). В полеPrecision(Точность) можно установить число знаков в различных формах отображения чисел в указанных справа границах; в полеImaginary (Мнимая единица) можно выбрать символ для отображения мнимой единицы (i или j). В нижней части окна расположены поля, позволяющие определить, применяются ли установки ко всему рабочему документу (Set as worksheet default) или только к текущей области ввода (Setfor current region only).
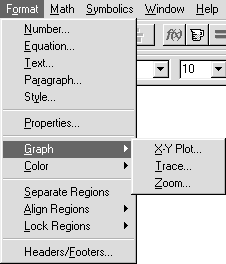
ПунктGraph (График) содержит операции форматирования графиков. Здесь, в зависимости от позиции курсора в рабочем документе и от определений, введенных в рабочий документ, открываются два различных дополнительных меню (рис. 11).
Рис. 11. Дополнительные меню настройки графиков
Когда курсор установлен вне поля двумерного декартова графика, открывается меню определения параметров графиковX-Y Plot, Polar Plot, 3D Plot — плоского декартова, полярного или трехмерного. Щелчок по соответствующей строке открывает окно настройки параметров изображения (см. описаниеGraph в менюInsert). Если же курсор установлен в открытом для ввода поле двумерного декартова графика, то дополнительное меню содержит строкиX-Y Plot — форматирование графика,Trace (Трассировка, След) — определение координат точки на помеченной линии иZoom (Микроскоп) — увеличение масштаба изображения помеченной области графика.
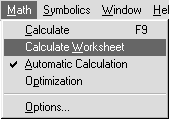 Рис. 12. Меню математики Рис. 12. Меню математики |
Меню Math (Математика). Это меню (рис. 12.) содержит операции управления вычислениями.
После щелчка поCalculate (Вычислить) = вычисляются выражения, расположенные выше и левее курсора*.
После щелчка по Calculate Worksheet (Пересчитать рабочий документ) выполняются все вычисления и перерисовываются все графики, определенные в рабочем документе.Если строкаAutomatic Calculation (Вычислять автоматически) помечена символом Ö, то любое выражение вычисляется немедленно после окончания ввода, а график строится после щелчка вне поля графиков. Если же пометка отсутствует, то вычисления и построения производятся только после соответствующей команды (щелчок поCalculate, например).Если строкаOptimization(Оптимизация) помечена символом Ö, то включен режим оптимизации вычислений. Режим оптимизации — это режим вычислений с включенным символьным процессором. В этом режиме сначала упрощаются все выражения, помещенные справа от знака присвоения :=, и только затем выражение обрабатывается числовым процессором. В противном случае числовой процессор обрабатывает выражение в исходном виде.
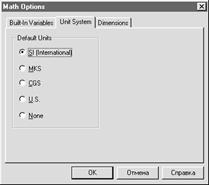
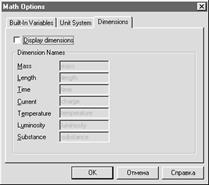
Щелчок по строке Options (Опции) открывает окно настройки режима вычислений (рис. 13), в котором можно определить Tolerance (Допуск) — допустимую погрешность численных алгоритмов, Array Origin (Начало массива) — номер первого элемента массива, Precision (Точность) — число значащих цифр при записи данных в файл, Column Width (Ширина столбца) — ширину столбца, используемую при записи данных в файл,Seed value for random numbers Начальное число для инициализации датчика случайных чисел)— число, инициализирующее датчик случайных чисел,Unit System (Система единиц) — систему единиц,Dimensions (Размерности) — размерности физических единиц. Все подлежащие изменению параметры заносятся в соответствующие поля ввода в окнах диалога.
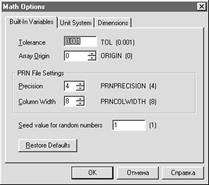
Рис. 13. Окна настройки параметров вычислений
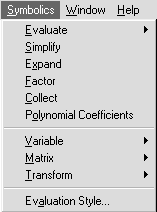 Рис. 14. Меню символьных операций Рис. 14. Меню символьных операций |
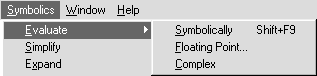 Рис. 15. Меню режимов вычислений Рис. 15. Меню режимов вычислений |
Меню Symbolics (Символьные вычисления). Это меню (рис. 14) содержит операции символьной математики. ПунктEvaluate (Вычислять) содержит три операции (рис. 15): Symbolically (Символьно),Floating Point (С плавающей запятой),Complex (Комплексное).
После щелчка по одной из этих трех строк вычисляется значение выделенного в рабочем документе выражения, причем вычисления производятся соответственно символьно, численно с плавающей запятой или с использованием арифметики комплексных чисел. Щелчком по строкеSimplify (Упростить) символьному процессору передается выражение, выделенное в рабочем документе, а преобразованное выражение отображается в рабочем документе ниже или справа от исходного выражения (см. описание опцииEvaluation Style). Совершенно аналогично после щелчка поExpand (Развернуть) в выделенном выражении раскрываются скобки, а после щелчка поFactor (Разложить на множители) выделенное выражение раскладывается на множители. В результате щелчка поCollect (Собрать) в выделенном выражении приводятся подобные.
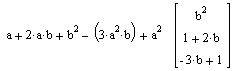 Рис. 16. Вычисление полиномиальных коэффициентов Рис. 16. Вычисление полиномиальных коэффициентов |
Если выражение является многочленом относительно выделенного фрагмента, то после щелчка по строкеPolynomial Coefficients (Коэффициенты полинома) в рабочий документ выводится вектор-столбец коэффициентов многочлена, записанных в порядке возрастания степеней выделенного выражения. На рис. 16 представлен результат такой операции, когда в исходном выражении выделено а.
Каждая из следующих трех строк (рис. 14) — Variable (Переменная), Matrix (Матрица),Transform (Преобразование) — объединяет группу символьных операций: символьные вычисления относительно выделенной переменной, символьные вычисления с выделенной матрицей и интегральные преобразования соответственно.
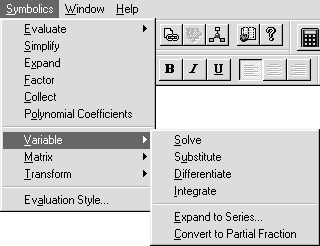 Рис. 17. Меню операций математического анализа Рис. 17. Меню операций математического анализа |
В пунктеVariable объединены операции математического анализа (рис. 17):
• решение уравнений (Solve);
• подстановка (Substitute);
(Differentiate);
• интегрирование (Integrate);
• разложение по формуле Тейлора(Expand to Series);
• разложение дроби на простейшие дроби (Convert to Partial Fraction).
Если в рабочем документе в некотором выражении выделена переменная, то после щелчка по соответствующей строке меню в рабочем документе отображается результат выполнения операции относительно выделенной переменной.
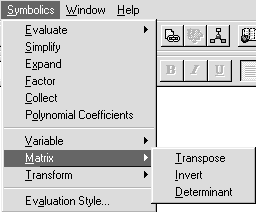 Рис. 18. Меню символьных операций с матрицами Рис. 18. Меню символьных операций с матрицами |
В пункте Matrix(рис. 18) объединены символьные вычисления с матрицами:
• Transpose (Транспонирование);
• Invert (Обращение) — вычисление обратной матрицы;
• Determinant (Определитель) — вычисление определителя квадратной матрицы.
Операции этой группы выполняются только, если в рабочем документе выделена матрица. Тогда после щелчка по строке меню в рабочем документе отображается результат выполнения соответствующей операции
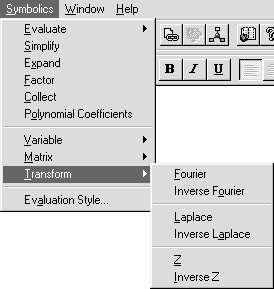 Рис. 19. Меню интегральных операции Рис. 19. Меню интегральных операции |
В пунктеTransform объединены символьные вычисления прямых и обратных интегральных преобразований (рис. 19) —Fourier и Inverse Fourier (преобразование Фурье),Laplace и Inverse Laplace(преобразование Лапласа),Z иInverse Z (Z-преобразование) — вычисление производящей функции.
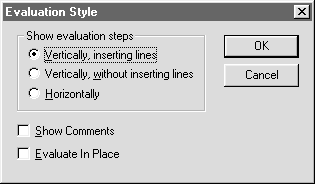 Рис. 20. Параметры формата символьных результатов Рис. 20. Параметры формата символьных результатов |
Щелчком по строке менюEvaluation Style (Стиль выражения) открывается окно, в котором определяется формат вывода результатов символьных вычислений (рис. 20).
В полеShow evaluation steps (Показать результаты вычислений) можно установить режим отображения результатов символьных вычислений в строке, расположенной непосредственно под исходные выражением(Vertically, inserting lines), прямо под исходным выражением (Vertically, without inserting lines) или справа от исходного выражения(Horizontally).
Меню Window (Окно). Это менв (рис. 21) позволяет устанавливать стиль расположения окон, содержащих различные рабочие документы Mathcad. Ок на можно расположить «каскадом», что бы они перекрывались, но при этом бы ли видны заголовки окон(Cascade), без перекрытия по горизонтали (Tile Horizontal) или по вертикали (Tile Vertical); можно также упорядочить ярлычки окон в панели задач (Arrange Icons). В нижней части меню расположен список всех окон, открытых в текущий момент. Щелчком по соответствующей строке можно вызвать на экран любое из окон.
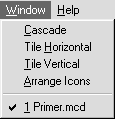 Рис. 21. Меню Окно Рис. 21. Меню Окно |
Панели инструментов MATHCAD
В окне Mathcad обычно располагаются три кнопочные панели инструментов (рис. 22).
Рис. 22. Панели инструментов
Верхняя — панельToolbar (Панель инструментов), большая часть кнопок которой стандартные для windows-приложений кнопки работы с файлами и текстом.
Средняя — панельFormat Bar (Панель форматирования), содержащая кнопки выбора шрифтов, размеров шрифтов, стиля (полужирный, наклонный, с подчеркиванием), а также кнопки форматирования текста на странице (выравнивание по левому краю, центрирование и выравнивание по правому краю);
Нижняя —Math Palette (Математическая палитра), каждая кнопка которой открывает дополнительную панель, содержащую кнопки операций с математическими объектами определенного класса.
Правила работы со всеми панелями одинаковы: щелчком по кнопке открываем вспомогательную панель, щелчком по кнопке выбираем в ней нужную операцию и заполняем в рабочем документе помеченные позиции для ввода данных, аргументов или параметров операции.
Панель Toolbar. Большинство кнопок этой панели дублируют меню File и Edit.
Панель Math Palette. Это панель математических инструментов (дословно «математическая палитра») — наиболее часто используемая панель, поскольку именно здесь расположены кнопки вычислительных операций и операций конструирования вычислительных процедур.
Панель математических инструментов содержит восемь кнопок, каждая из которых открывает дополнительную панель математических операций. Далее, в начале каждой главы, описаны дополнительные панели математических операций, наиболее часто используемые при решении задач главы. Здесь же просто перечислены кнопки панели математических операций и приведен вид каждой дополнительной панели.
 Рис. 23. Панель калькулятора Рис. 23. Панель калькулятора |
Кнопка —Arithmetic Palette (Калькулятор) открывает панель простейших вычислений (рис.23).
Щелчком по кнопке этой панели в рабочий документ вставляем имя функции, символ, цифру или знак операции с помеченными для ввода позициями:
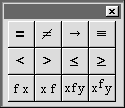 Рис. 24. Панель отношении Рис. 24. Панель отношении |
Кнопка —Evaluation and Boolean Palette (Панель равенств и отношений) откпывает панель, изображенную на рис. 24.
Щелчком по кнопкам этой панели в рабочий документ вставляются соответствующие знаки отношений:
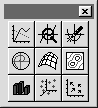 Рис. 25. Панель графиков Рис. 25. Панель графиков |
Кнопка —Graph Palette (Панель графиков) открывает панель, изображенную на рис. 25.
Щелчком по кнопке этой панели в рабочий документ вставляем поле графика соответствующего типа.
Кнопка —Vector and Matrix Palette (Панель векторных и матричных операций) открывает панель, изображенную на рис. 26.
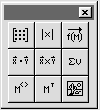 Рис.26. Панель матричных операций Рис.26. Панель матричных операций |
Кнопка — Calculus Palette (Панель операций математического анализа) открывает панель, изображенную на рис. 27.
Кнопка—Programming Palette (Панель программирования) открывает панель, представленную на рис. 28.
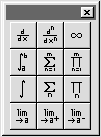 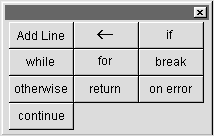 Рис. 27. Панель операций Рис. 28. Панель программирования математического анализа Рис. 27. Панель операций Рис. 28. Панель программирования математического анализа |
Кнопка —Greek SymbolPalette (Панель греческих букв) открывает панель, изображенную на рис. 29.
Кнопка —Symbolic Keyword Palette (Ключевые слова символьных вычислений) открывает панель, изображенную на рис. 30.
  Рис. 29. Панель греческих букв Рис. 30. Панель ключевых слов Рис. 29. Панель греческих букв Рис. 30. Панель ключевых слов |
Видно, что кнопки панели дублируют соответствующие пункты меню символьных операций. Щелчком по кнопке вставляем в рабочий документ ключевое слово с помеченными позициями для ввода данных.
Примеры решения задач элементарной математики в MATHCAD
Большинство вычислений в Mathcad можно выполнить тремя способами — выбором операции в меню, с помощью кнопочных панелей инструментов или обращением к соответствующим функциям.
📺 Видео
8. MathCad. Решение систем линейных алгебраических уравненийСкачать

Ключевое слово solve в MathCAD 14 (26/34)Скачать

MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

Mathcad-09. Пример: уравненияСкачать

Пример решения уравнения в MathCAD 14 (33/34)Скачать

MathCAD. Given - FindСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение матричных уравненийСкачать

Математика без Ху!ни. Метод Гаусса.Скачать