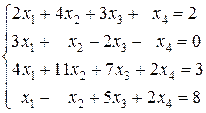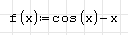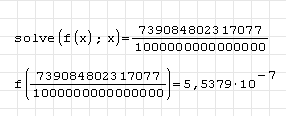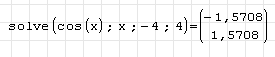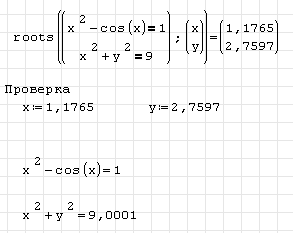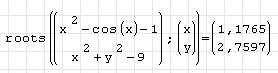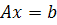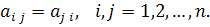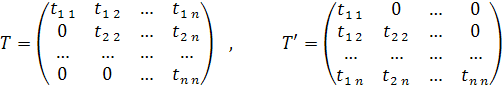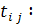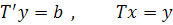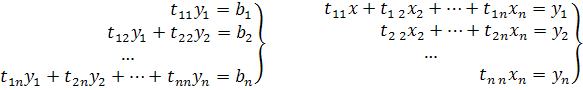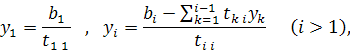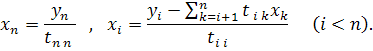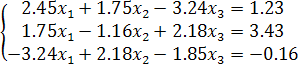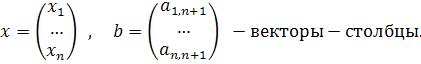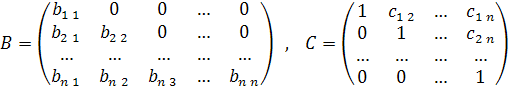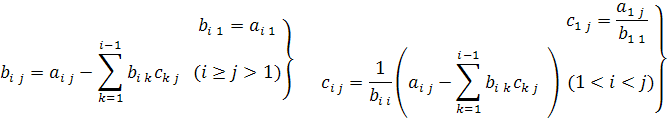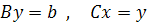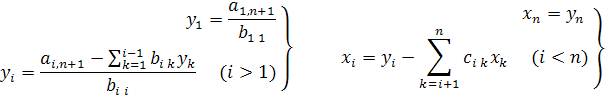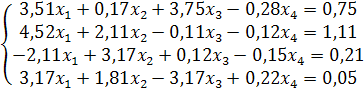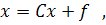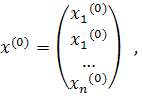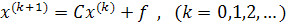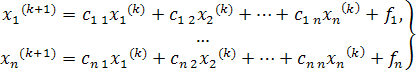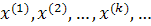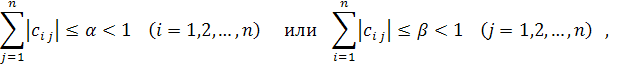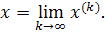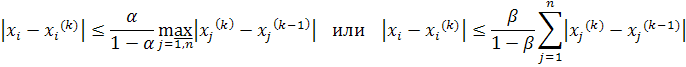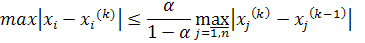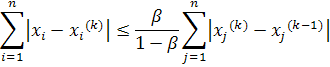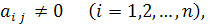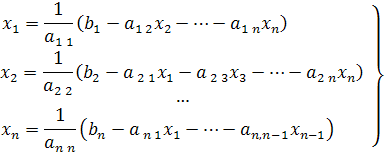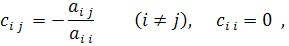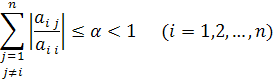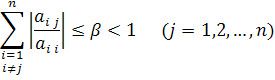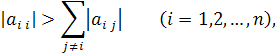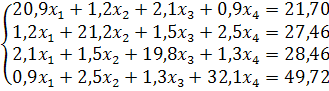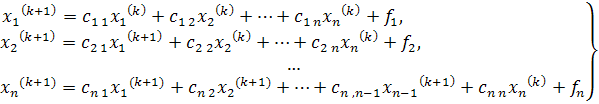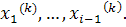Решение уравнений матричным методом в smath studio

Решение нелинейных уравнений

Пример 3.1. Найти корень уравнения x – sin x – 0,25 = 0 на отрезке [0,2] с точностью 0,0001.

MathCAD

Для решения одного нелинейного уравнения с одной неизвестной система MathCAD имеет встроенную функцию, которая в зависимости от типа задачи может иметь или два или четыре аргумента и, соответственно, работает несколько по-разному: root(f(x),x); root(f(x),x,a,b), где f(x) — скалярная функция, определяющая исходное нелинейное уравнение (4.1); х – скалярная переменная, относительно которой решается уравнение; а, b – границы интервала, внутри которопй происходит поиск корня.

Первый тип функции root требует предварительного задания начального приближения х₀ переменной х. Поиск корня будет производиться вблизи этого значения методом секущих. Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в области локального максимума или минимума функции f(x). В этом случае секущая будет иметь направление, близкое к горизонтальному, выводя точку следующего приближения далеко от предполагаемого корня. Аналогичные проблемы могут возникнуть, если начальное приближение выбрано слишком далеко от настоящего решения, или f(x) имеет особенность типа бесконечности.

Иногда удобнее задавать не начальное приближение к корню, а интервал [а, b], внутри которого заведомо находится корень. В этом случае следует использовать функцию root с четырьмя аргументами; присваивать начальное значение переменной х в этом случае не нужно. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента).

Решение (распечатка MathCAD)
f(x) := x – sin(x) – 0.25 x := 0,0.1..2 х := 1 – начальное приближение s := root(f(x), x) s =1.171 — корень уравнения f(s)=–4.836´10 –5 — погрешность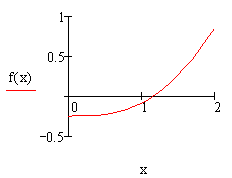

SMath Studio

Для решения одного нелинейного уравнения с одной неизвестной система SMath Studio имеет встроенную функцию, которая в зависимости от типа задачи может иметь или два или три аргумента: roots(f(x); x) или roots(f(x); x; a), где f(x) – скалярная функция, определяющая исходное нелинейное уравнение (4.1); х – скалярная переменная, относительно которой решается уравнение; а – начальное приближение переменной х.

Решение (распечатка SMath Studio)

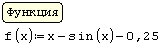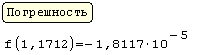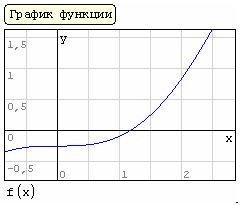Решение систем линейных алгебраических уравнений

Пример 3.2. Решить систему уравнений

MathCAD

Для решения систем уравнений в среде MathCAD можно применять вычислительный блок Given/Find. Он состоит из трех частей:

1. ключевое слово Given;

2. система уравнений, записанная с помощью логических операторов;

3. вызов встроенной функции Find(xl, х2. хп).

Перед применением блока Given/Find необходимо задать начальные значения переменным xl, x2,хп.

Однако более наглядным является решение СЛАУ в матричной форме. В этом случае используется встроенная функция lsolve(A,b), где А — матрица коэффициентов системы, b — вектор правых частей.

Решение (распечатка MathCAD)

Решение с помощью вычисли­тель­ного блока Given/Find	Решение с помощью встроенной функции lsolve
xl :=1 х2:=1 х3:= 1 х4:=1 Given 2·xl + 4·х2 – 3·хЗ + х4 = 2 3·xl + х2 – 2·хЗ — х4 = 0 4·xl +11·х2 + 7·х3 + 2·х4 = 3 xl – x2 + 5·x3+2·x4 = 8 y := Find(xl ,х2,хЗ,х4)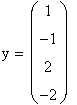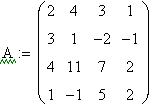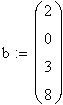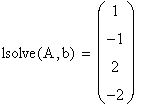

SMath Studio

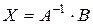
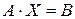
Для решения систем уравнений в среде SMath Studio применяется матричный метод решения: коэффициенты левых частей уравнений записываются в квадратную матрицу A размером 4´4, свободные коэффициенты записываются в столбец B размером 4´1. Решением будет столбец X, который находится умножением обратной матрицы на столбец B: . Решение существует, если определитель матрицы A не равен нулю. Получив решение, нужно сделать проверку, т.е. убедиться, что .

Видео:Матричный метод решения систем уравненийСкачать

Пример выполнения задания 2

Модуль 2

Решение иженерных задач средствами

Компьютерной математики

Лабораторная работа № 2

Нахождение корней нелинейных уравнений. Решение систем нелинейных уравнений

Цель: изучить основные возможности приложения Smath Studio для решения нелинейных уравнений и систем.

Вопросы для самоконтроля

1. Что является корнем уравнения?

2. Правило записи функции для использования команды solve.

3. В чем разница между численным и аналитическим нахождением корней уравнения?

4. Чем отличаются команды solve(2) и solve(4).

5. Для чего используется функция polyroots?

6. Правило записи вектора коэффициентов для polyroots.

7. Что является решение системы уравнений?

8. Правило записи уравнений для использования команды roots.

9. В чем разница между численным и аналитическим решениями системы уравнений?

10. Чем отличаются команды roots (2) и roots (3).

Индивидуальные задания 1

Найти корень уравнения численно и, если это возможно, аналитически. Результаты сравнить. Выполнить проверку.

№ варианта	Уравнение	№ варианта	Уравнение

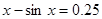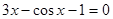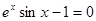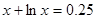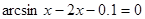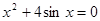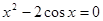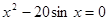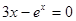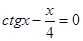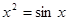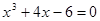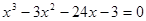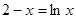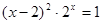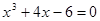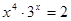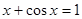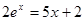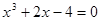Индивидуальные задания 2

Найти численно корни полинома. Выполнить проверку.

Индивидуальные задания 3

Найти численное решение системы. Выполнить проверку.

№ варианта	Система уравнений	Начальная точка
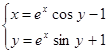	(-0,9;1,4)
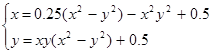	(1;1)
	(1;1)
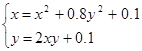	(0;0)
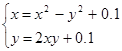	(0;0)
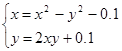	(0;0)
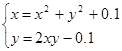	(0;0)
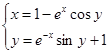	(0,9;1,4)
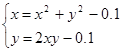	(0;0)

№ варианта	Система уравнений	Начальная точка
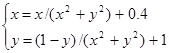	(1;1)
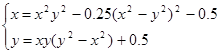	(-0,5;0,5)
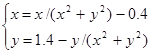	(-1;1)
	(0;0)
	(0;0)
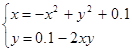	(0;0)
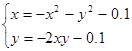	(0;0)
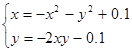	(0;0)
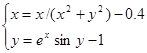	(-1;1)
	(-0,9;-1,4)
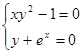	(0,5;-1,5)
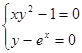	(0,5;1,5)
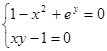	(2;2)
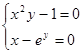	(1,5;0,5)
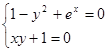	(-2;2)
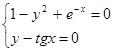	(0;1)

Пример выполнения задания 1

Найти корень уравнения 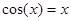численно и, если это возможно, аналитически. Результаты сравнить. Выполнить проверку.

Методические рекомендации

1. Запишите функцию (предварительно приведя уравнение к виду f(x)=0): .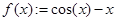

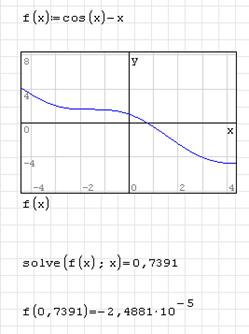
2. Постройте график функции. График пересекает ось абсцисс в одной точке, значит, уравнение имеет один корень.

3. Запишите стандартную команду:

Справа от знака равенства увидим результат: 0,7391.

2 Выполните проверку, найдя значение функции в полученной точке:

.

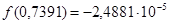
Если бы решение было точным, то при проверке получили бы 0. Значение 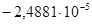означает, что результат получен с точностью до 4-го знака.

Конечный вид документа SMathStudio:

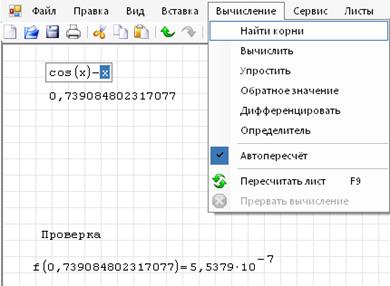
1. Запишите функцию в виде: .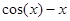

2 Выделите курсором переменную х.

3. В меню выбрать Вычисление ® Найти корни.

4. Выполните проверку.

1. Конечный вид документа SMathStudio:

1. Запишите функцию: .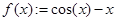

2. Для получения аналитического решения запишите стандартную команду:

solve(f(x) ; x), после которой на ПИ «Арифметика» выберите →.

3. Выполните проверку, найдя значение функции в полученной точке.

Конечный вид документа SMathStudio:

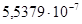
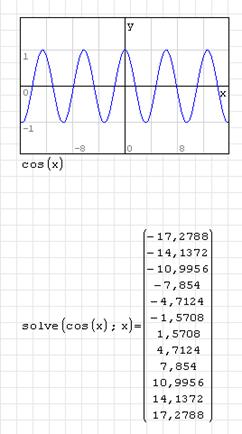
Если бы решение было точным, то при проверке получили бы 0. Значение означает, что результат получен с точностью до 4-го знака. Делаем вывод, что SMathStudio не может найти точные корни данного уравнения.

Если уравнение имеет несколько корней (как, например, уравнение 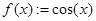), то применение стандартной процедуры решения даст ответ в виде вектора:

Корни выдаются в диапазоне «по умолчанию» [-20; 20]. Изменить диапазон можно в меню Сервис – Опции – Вычисление.

Можно использовать второй вариант этой процедуры для выбора решения на заданном промежутке. Для этого при наборе solve во всплывающей подсказке выбираем solve(4) и в шаблон вписываем:

Solve( ; ; левая граница интервала; правая граница интервала). Получим:

Если функция f(x) в уравнении f(x)=0 представляет собой полином степени n, то процедура solve может выдать только один корень. Чтобы получить все корни полинома (их количество совпадает со степенью полинома), стоит использовать встроенную функцию polyroots(v). Например, найдем численно корни полинома x 3 +2x-1=0.

1) задаем функцию (левую часть уравнения f(x)=0).

2) задаем вектор коэффициентов (кнопка на ПИ «Матрица»), в появившемся диалоговом окне указываем количество строк (равно степени полинома +1) и столбцов (количество уравнений).

3) записываем функцию polyroots(v)=.

4) делаем проверку, подставив найденные значения в функцию.

Конечный вид документа Smath Studio:

Пример выполнения задания 2

Решить систему уравнений 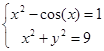численно и, если это возможно, аналитически. Результаты сравнить. Выполнить проверку.

Методические рекомендации

1. Записываем функцию roots( ; ).

2. Для получения численного решения ставим знак «=». Получим результат с заданным количеством знаков после запятой.

3. Выполняем проверку, подставив полученные значения в исходную систему уравнений. В данном примере 1-ое уравнение решено точно, 2-ое – с точностью до 3-го знака.

4. Вид документа SMathStudio:

Можно каждое уравнение системы привести к виду f(x)=0. Тогда запись решения будет выглядеть следующим образом:

Если нужно получить одно из нескольких возможных решений, можно задать начальное приближение (координаты ближайшей известной к ответу точки) для переменных следующим образом:

Видео:Решение СЛАУ в SMathСкачать

МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

Метод квадратных корней.

Метод квадратных корней используется для решения линейной системы:

У которой матрица А симметрическая, т.е.

Он является более экономным и удобным по сравнению с методами решения систем общего вида, рассмотренными ранее.

Решение системы осуществляется в два этапа.

Прямой ход. Представим матрицу А в виде произведения двух взаимно транспонированных треугольных матриц:

Перемножая матрицы Т’ и Т и приравнивая матрице A, получим следующие формулы для определения

После того, как матрица Т найдена, систему заменяем двумя эквивалентными ей системами с треугольными матрицами:

Обратный ход. Записываем в развернутом виде системы:

Отсюда последовательно находим:

При вычислениях применяется обычный контроль с помощью сумм, причем при составлении суммы учитываются все коэффициенты соответствующей строки.

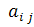
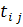
Заметим, что при действительных могут получиться чисто мнимые . Метод применим и в этом случае .

Метод квадратных корней дает большой выигрыш во времени по сравнению с рассмотренными ранее методами, так как, во-первых, существенно уменьшает число умножений и делений (почти в два раза для больших n), во-вторых, позволяет накапливать сумму произведений без записи промежуточных результатов.

Задание. Решить систему линейных уравнений методом квадратных корней.

Провести эту работу в SMathStudio.

Схема Халецкого.

Рассмотрим систему линейных уравнений, записанную в матричном виде:

Где 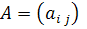— квадратная матрица (i, j = 1, 2, . , n) и

Представим матрицу А в виде произведения А=ВС, где

Тогда элементы 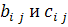будут определяться по формулам

Отсюда искомый вектор х может быть вычислен из цепи уравнений

Так как матрицы B и С треугольные, то системы легко решаются, а именно:

Из формул видно, что числа 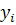выгодно вычислять вместе с коэффициентами Эта схема вычислений называется схемой Халецкого. В схеме применяется обычный контроль с помощью сумм.

Схема Халецкого удобна для работы на клавишных вычислительных машинах, так как в этом случае операции «накопления» можно проводить без записи промежуточных результатов.

Задание. Решить систему линейных уравнений методом Халецкого.

Провести эту работу в SMathStudio.

Метод простой итерации

Пусть система линейных уравнений

Каким-либо образом приведена к виду

где С – некоторая матрица, а f – вектор-столбец.

Исходя из произвольного вектора ,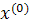

сторим итерационный процесс

или в развернутой форме

Производя итерации, получим последовательность векторов

Доказано, что если элементы матрицы С удовлетворяют одному из условий

то процесс итерации сходится к точному решению системы х при любом начальном векторе 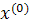, т.е.

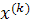
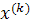
Таким образом, точное решение системы получается лишь в результате бесконечного процесса и всякий вектор из полученной последовательности является приближенным решением. Оценка погрешности этого приближенного решения дается одной из следующих формул:

Эти оценки можно усилить соответственно так:

Процесс итераций заканчивают, когда указанные оценки свидетельствуют о достижении заданной точности.

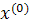
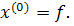
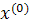
Начальный вектор может быть выбран, вообще говоря, произвольно. Иногда берут Однако наиболее целесообразно в качестве компонент вектора взять приближенные значения неизвестных, полученные грубой прикидкой.

Первый способ. Если диагональные элементы матрицы А отлины от нуля, т. е.

то систему можно записать в виде:

В этом случае элементы матрицы С определяются следующим образом:

и тогда условия приобретают вид:

Неравенства будут выполнены, если диагональные элементы матрицы А удовлетворяют условию:

т.е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).

Второй способ покажем на примере.

Вообще говоря, для любой системы с невырожденной матрицей существуют сходящиеся итерационные методы решения, но далеко не всегда они удобны для практических вычислений.

Если метод итераций сходится, он дает следующие преимущества по сравнению с методами, рассмотренными выше.

1) Если итерации сходятся достаточно быстро, т. е. если для решения системы требуется менее n итераций, то получаем выигрыш во времени, так как число арифметических действий, необходимых для одной итерации, пропорционально n 2 , а общее число арифметических действий в методе Гаусса, например, пропорционально n 3 .

2) Погрешности округления в методе итераций сказываются значительно меньше, чем в методе Гаусса. Кроме того, метод итераций является самоисправляющимся, т. е. отдельная ошибка, допущенная в вычислениях, не отражается на окончательном результате, так как ошибочное приближение можно рассматривать как новый начальный вектор.

Последнее обстоятельство часто используется для уточнения значений неизвестных, полученных методом Гаусса.

3) Метод итераций становится особенно выгодным при решении систем, у которых значительное число коэффициентов равно нулю. Такие системы появляются, например, при решении уравнений в частных производных.

4) Процесс итераций приводит к выполнению однообразных операций и сравнительно легко программируется на ЭВМ.

Задание. Решить систему линейных уравнений методом простых итераций.

Провести эту работу в SMathStudio.

Метод Зейделя.

Метод Зейделя является модификацией метода простой итерации. Он заключается в том, что при вычислении (k + 1)-го приближения неизвестного x_i при i>1 используются уже вычисленные ранее (k + 1)-е приближения неизвестных 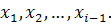Таким образом, для системы вычисления по методу Зейделя ведутся по формулам:

Указанные в методе простой итерации условия сходимости остаются верными и для метода Зейделя. Обычно метод Зейделя дает лучшую сходимость, чем метод простой терации, хотя это бывает не всегда. Кроме того, метод Зейделя может оказаться более удобным при программировании, так как при вычислении 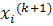нет необходимости хранить значения

Задание. Решить систему линейных уравнений методом Зейделя.

📺 Видео

SMath Studio - Урок 3 - Решение систем уравненийСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Решение СЛУ в SMathСкачать

Матрицы в SMath StudioСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Решение матричных уравненийСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

решение уравнений и систем уравнений в SmathСкачать

Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать

Нахождение обратной матрицы методом Жордано-ГауссаСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Решение математических задач в программе SMath StudioСкачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

Решение системы уравнений методом Крамера.Скачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение СЛАУ в пакете MathCadСкачать

Решение системы уравнений методом ГауссаСкачать