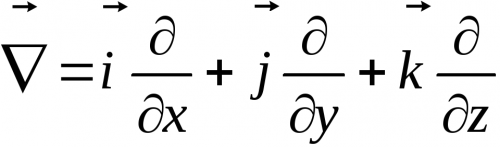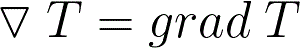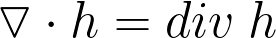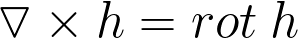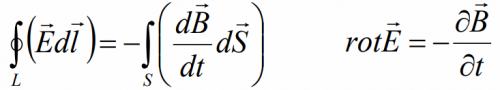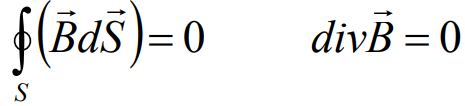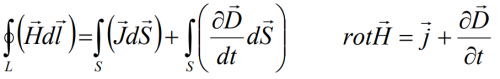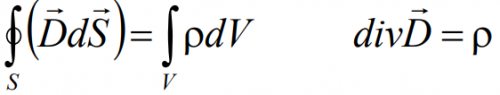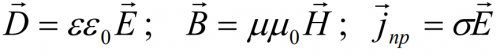- М. : Просвещение, 1990, 272 с.
- Учение об электромагнитном поле в вакууме
- Глава I. Основные понятия и принципы электродинамики
- Глава II. Стационарное электромагнитное поле
- Глава III. Электромагнитные волны и излучение электромагнитных волн
- Глава IV. Релятивистская формулировка электродинамики
- Электромагнитное поле и процессы в веществе
- Глава V. Основные понятия и уравнения электромагнитного поля в веществе
- Глава VI. Элементы электростатики
- Глава VII. Постоянный электрический ток. Магнитное поле тока
- Глава VIII. Квазистационарное электромагнитное поле и квазистационарные процессы
- Глава IX. Электромагнитные волны в веществе
- Презентация на тему «КВАЗИСТАЦИОНАРНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ»
- Описание презентации по отдельным слайдам:
- Уравнения Максвелла для электромагнитного поля — основные законы электродинамики
- Квазистационарное приближение
- 🔥 Видео
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

М. : Просвещение, 1990, 272 с.
Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Учение об электромагнитном поле в вакууме
Глава I. Основные понятия и принципы электродинамики
§ 1. Электрический заряд и электромагнитное поле
1.1. Заряд. Плотность заряда и плотность тока. 1.2. Закон сохранения заряда. 1.3. Электромагнитное поле. Напряженность электрического поля. Индукция магнитного поля.
§ 2. Система уравнений Максвелла — основа электродинамики
2.1. Уравнение Максвелла для системы зарядов в вакууме. 2.2. Интегральная форма уравнений Максвелла. Графическое изображение полей. 2.3. Связь уравнений Максвелла с эмпирическими законами электромагнитных явлений. 2.4. Принцип суперпозиции полей. 2.5. Задачи электродинамики. 2.6. Уравнения Максвелла-Лоренца. Принцип причинности в электродинамике.
§ 3. Энергия и импульс электромагнитного поля
3.1. Работа, совершаемая полем при перемещении зарядов. 3.2. Энергия электромагнитного поля. Плотность и поток энергии. Закон изменения энергии. 3.3. Закон сохранения энергии для изолированной системы поле-заряды. 3.4. Импульс электромагнитного поля. Закон сохранения импульса
§ 4. Уравнения для потенциалов электромагнитного поля
4.1. Потенциалы электромагнитного поля. 4.2. Уравнения электромагнитного поля в потенциалах. 4.3. Понятие об общем решении уравнений поля в потенциалах
§ 5. Решения уравнений поля
5.1. Свободное электромагнитное поле. Плоские волны. 5.2. Гармонические составляющие свободного поля. 5.3. Сферические волны. 5.4. Потенциалы поля стационарной системы движущихся зарядов. 5.5. Запаздывающие потенциалы. 5.6. Характерные особенности и итоги общей задачи о расчете полей
Глава II. Стационарное электромагнитное поле
§ 6. Стационарное электрическое поле в вакууме
6.1. Особенности стационарных полей. 6.2. Уравнения стационарного электрического поля в потенциалах. 6.3. Электростатическое поле и закон Кулона. 6.4. Электростатическое поле системы зарядов на большом удалении. Дипольный момент системы
§ 7. Работа и энергия электростатического поля. Сила действующая на жесткую систему зарядов
7.1. Система зарядов во внешнем электростатическом поле. Работа и потенциальная энергия. 7.2. Силы, действующие на жесткую систему зарядов во внешнем поле. 7.3. Энергия взаимодействия зарядов и энергия электростатического поля
§ 8. Магнитостатическое поле в вакууме
8.1. Уравнения магнитостатического поля в потенциалах. 8.2. Векторный потенциал и индукция магнитостатического поля. 8.3. Магнитное поле в дипольном приближении. 8.4. Энергия системы движущихся зарядов во внешнем магнитном поле. Сила, действующая на систему. 8.5. Энергия магнитостатического поля
Глава III. Электромагнитные волны и излучение электромагнитных волн
§ 9. Плоские электромагнитные волны
9.1. Уравнение Максвелла и образование электромагнитных волн. 9.2. Векторы напряженности и индукции плоской электромагнитной волны. 9.3. Гармонические составляющие свободного поля. 9.4. Поляризация электромагнитных волн
§ 10. Излучение электромагнитных волн
10.1. Потенциалы электромагнитного поля вдали от системы зарядов. 10.2. Электрическое дипольное излучение. 10.3. Магнитное дипольное излучение. 10.4*. Понятие о волновой и квазистатической зонах. 10.5*. Спектральное разложение излучения
§ 11. Рассеяние электромагнитных волн свободным зарядом
11.1. Постановка вопроса о движении заряда в электромагнитном поле. 11.1. Рассеяние электромагнитных волн свободным зарядом
Глава IV. Релятивистская формулировка электродинамики
§ 12. Релятивистская ковариантность уравнений электродинамики
12.1. Четырехмерный вектор плотности тока. Четырехмерная форма закона сохранения заряда. 12.2. Ковариантность уравнений электромагнитного поля в потенциалах
§ 13. Тензор электромагнитного поля. Преобразование векторов напряженности и индукции электромагнитного поля при переходе от одной инерциальной системы к другой
13.1. Тензор электромагнитного поля. 13.2. Преобразование векторов поля Е и В при переходе от одной инерциальной системы к другой. Инварианты поля. 13.3. Эффект Доплера для электромагнитных волн
Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Электромагнитное поле и процессы в веществе
Глава V. Основные понятия и уравнения электромагнитного поля в веществе
§ 14. Усреднение уравнений микроскопического поля в веществе
14.1. Свободные и связанные заряды. 14.2. Усредненные уравнения поля для системы свободных и связанных зарядов. 14.3. Уравнения Максвелла—Лоренца для микроскопического поля в электронной теории. 14.4. Макроскопическое усреднение уравнений Максвелла—Лоренца
§ 15. Уравнения Максвелла для поля в веществе
15.1. Поляризация вещества в электрическом поле. 15.2. Намагничивание вещества. 15.3. Уравнения Максвелла для поля в веществе. Напряженность магнитного и индукция электрического полей. 15.4. Магнитная и электрическая проницаемости вещества. Материальные уравнения
§ 16. Характерные особенности полей в веществе
16.1. Уравнения поля в потенциалах. 16.2. Граничные условия. 16.3. Энергия и импульс поля в веществе
Глава VI. Элементы электростатики
§ 17. Электростатика диэлектриков
17.1. Электростатическое поле в однородном диэлектрике. 17.2. Электростатическое поле при наличии границ раздела в среде и разрывов непрерывности плотности зарядов
§ 18. Проводники в электростатическом поле
18.1. Уединенный проводник. Электроемкость. 18.2*. Система проводников. 18.3. Энергия электростатического поля как энергия взаимодействия системы тел. 18.4. Силы, действующие на тела в электростатическом поле
Глава VII. Постоянный электрический ток. Магнитное поле тока
§ 19. Уравнения Максвелла и законы постоянного тока
19.1. Структура электрического поля постоянного тока. 19.2. Стороннее поле и закон Ома в дифференциальной форме. 19.3. Поле замкнутой цепи с постоянным током. 19.4. Интегральный закон Ома для замкнутой цепи. Закон Джоуля—Ленца
§ 20. Магнитное поле постоянных линейных токов
20.1. Закон Био-Савара. 20.2. Понятие о магнитостатике магнетиков. 20.3. Энергия магнитного поля постоянных токов. Коэффициенты индукции. 20.4. Механические силы, действующие в магнитном поле. Формула Ампера
Глава VIII. Квазистационарное электромагнитное поле и квазистационарные процессы
§ 21. Уравнения квазистационарного поля. Электромагнитная индукция
21.1. Условия квазистационарности. 21.2. Уравнения квазистационарного поля. 21.3. Закон электромагнитной индукции Фарадея
Глава IX. Электромагнитные волны в веществе
§ 23. Электромагнитные волны в веществе
23.1. Плоские волны в идеальном диэлектрике. 23.2*. Электромагнитные волны в однородной проводящей среде. 23.3. Отражение и преломление электромагнитных волн на границе двух диэлектриков
§ 24. Электромагнитная природа света
24.1. Свет — электромагнитные волны. 24.2. Световое поле. 24.3*. Принцип Гюйгенса-Френеля. 24.4. Геометрическая оптика как предельный случай волновой. 24.5. Дисперсия диэлектрической проницаемости. 24.6. Зависимость диэлектрической проницаемости от напряженности поля. Понятие о нелинейной оптике. 24.7. Границы применимости классической электродинамики в оптике
Видео:60. Уравнения МаксвеллаСкачать

Презентация на тему «КВАЗИСТАЦИОНАРНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
311 лекций для учителей,
воспитателей и психологов
Получите свидетельство
о просмотре прямо сейчас!
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
ЭЛЕКТРОДИНАМИКА СПЛОШНЫХ СРЕД ЛЕКЦИЯ 10 КВАЗИСТАЦИОНАРНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ
ПЛАН ЛЕКЦИИ 1. Условия квазистационарности 2. Уравнение Максвелла для квазистационарных полей 3. Закон индукции в движущихся проводниках 4. Закон Ома для цепи переменного тока 5. Интегрирование уравнений Максвелла 6. Коэффициенты индукции 7. Вычисление коэффициентов индукции
Уравнения Максвелла: R a — период движения заряда — время запаздывания — напряженность электрического поля
Условия квазистационарности Существует широкий интервал частот изменений полей, в котором уравнения Максвелла допускают существенные упрощения. Они состоят в следующем: 1. Пусть заряды движутся со скоростями v > (1) (первое условие квазистационарности). Поля, для которых можно пренебречь условиями запаздывания, называются квазистационарными. 2. Из (1) следует, что периоды должны быть достаточно большими, а частоты малыми. Это означает, что в уравнениях Максвелла: — ток проводимости много больше тока смещения — второе условие. 3. Третьим условием квазистационарности является требование, чтобы величины характеризующие свойства вещества — , . имели такие же значения, что и в постоянных полях. (2)
Уравнения Максвелла для квазистационарных полей Уравнения квазистационарного электромагнитного поля имеют вид: (3) Уравнение непрерывности запишется, как Их следует дополнить уравнениями связи: Таким образом, отличие квазистационарных полей от полей стационарных токов сводится к учету явлений электромагнитной индукции
Закон индукции в движущихся проводниках Движение проводников в магнитном поле имеет большое практическое значение, так как на этом основывается принцип действия динамомашин и метод возбуждения ЭДС. Обобщим понятие потока индукции для случая движущихся контуров с током. Для этого найдем изменение потока индукции через контур с проводником: S1 S2 Sбок Из интегрального уравнения Максвелла: найдем, что: (4) (5)
Закон индукции в движущихся проводниках Окончательно из (5): Подставим это в (4) и найдем: (6) Изменение потока индукции через контур во времени может происходить либо вследствие изменения вектора индукции, либо вследствие движения контура с током в заданном поле, но так, чтобы векторное произведение скорости и индукции не было равно нулю. Теперь можем записать закон индукции Фарадея для движущегося контура с током: — напряженность поля в линейном проводнике. (7)
Закон Ома для цепи переменного тока Уравнения Максвелла для квазистационарных полей в интегральной форме запишутся: Уравнение непрерывности Для одного линейного проводника с током в контуре, содержащим заданную стороннюю ЭДС, обобщенный закон Ома в интегральной форме имеет вид Так как то (9) Это уравнение называют законом Ома для цепи переменного тока. — сторонняя ЭДС. (8)
Интегрирование уравнений Максвелла Для системы, состоящей из N контуров с переменным током, можно записать где Фi — поток индукции через i-й контур. Соотношение (10) связывает распределение магнитного поля и тока в цепи. В квазистационарных полях потоки индукции оказываются связанными с плотностями токов линейными соотношениями с постоянными коэффициентами: (10) 1 Доказательство: (11) 2
Коэффициенты индукции Наряду с Ф1(2) имеется поток индукции, создаваемый первым током в самом первом контуре: Ф1(1)=сL11I1, L11 – коэффициенты самоиндукции. Происхождение коэффициентов самоиндукции таково: поток магнитной индукции через некоторый участок провода получается суммированием потоков создаваемых другими его участками. При этом во всех участках провода течет ток I1. Ясно, что для коэффициентов самоиндукции предыдущую формулу использовать нельзя, так как возникнет расходимость: Коэффициенты взаимной индукции L12 зависят только от свойств среды и взаимного расположения контуров и определяются : (12)
Полный поток магнитной индукции через первый проводник можно записать Ф1=сL11I1+cL12I2, Ф2=сL21I1+cL22I2 , а обобщенный закон Ома в первом контуре примет вид: Коэффициенты индукции В общем случае для N контуров: Доказать самостоятельно, что L12=L21. (13) (14)
Вычисление коэффициентов индукции Энергия магнитного поля, сосредоточенная в объеме V Поток магнитного поля через поверхность S определяется Энергия взаимодействия двух токов может быть определена как: Магнитный поток взаимодействия двух токов: С другой стороны их можно вычислить через коэффициент взаимной индукции L12: W12=L12I1I2, Ф12=L12I2 который для случая линейных токов определяется:
Вычисление коэффициентов индукции Задача. Внутри тонкой проводящей цилиндрической оболочки радиуса a находится коаксиальный провод радиуса b, магнитная проницаемость которого 0. Пространство между проводом и оболочкой заполнено веществом с магнитной проницаемостью . Найти коэффициент самоиндукции L такой линии на единицу длины. a b Решение. Для того чтобы определить коэффициент самоиндукции, надо найти энергию магнитного поля. Её мы можем вычислить, если знаем распределение магнитного поля во всем пространстве. Найдем вектор из теоремы о циркуляции: Система координат цилиндрическая, ось z совпадает с направлением тока. Выберем в качестве произвольного контура интегрирования окружность с радиусом r и центром на оси проводника. Площадь, охватываемая контуром, равна S и нормаль к этой поверхности совпадает с вектором . Ввиду аксиальной симметрии напряженность магнитного поля зависит только от расстояния до оси провода и имеет только -ю составляющую Н.
Вычисление коэффициентов индукции в пространстве между проводом и оболочкой (а b) Таким образом, напряженность и индукция поля
Вычисление коэффициентов индукции Энергия магнитного поля С другой стороны Поэтому коэффициент самоиндукции на единицу длины линии l:
Контрольные вопросы 1. Докажите, что при определенных условиях период движения зарядов много больше, чем время запаздывания. 2. Из какого уравнения Максвелла и при каком условии возникает второе условие квазистационарности? 3. Доказать, что второе условие квазистационарности можно записать в виде T>>/ 4. Что понимается под термином переменные токи? 5. Сформулируйте закон индукции Фарадея. 6. Какие величины связывает между собой закон Ома для цепи переменного тока? 7. Какой смысл имеет коэффициент взаимной индукции? 8. Доказать, что коэффициенты взаимной индукции удовлетворяют свойству L12=L21
Уравнения Максвелла для электромагнитного поля — основные законы электродинамики
Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.
Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.
Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.
Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).
Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.
Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.
В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.
Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.
Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:
где i, j и k – единичные координатные векторы
Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:
Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.
Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.
Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.
Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.
Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.
Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.
Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.
Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.
Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.
Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.
Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.
Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.
Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.
Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.
Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.
Физический смысл: источником электрического поля является электрический заряд.
Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды:
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Не пропустите обновления, подпишитесь на наши соцсети:
Видео:Вывод уравнений МаксвеллаСкачать

Квазистационарное приближение
Квазистационарное (квазистатическое) приближение в электродинамике – это приближенное описание переменного электромагнитного поля (ЭМП), справедливое при достаточно медленных его изменениях во времени. Классификация приближений обычно основывается на безразмерных параметрах. Для электромагнитных полей в вакууме таким параметром может быть отношение
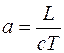
где 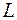
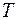
В соответствии с формулой (104.1) можно выделить четыре случая.
1. 
А. В соответствии с этим система уравнений Максвелла для описания электростатических полей имеет вид
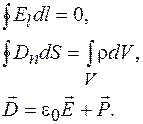
Источниками полей в электростатике служат заданные распределения плотности электрического заряда 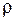
Б. Система уравнений Максвелла для описания полей в магнитостатике приобретает вид
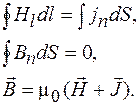
Источниками в уравнениях магнитостатики являются заданные распределения плотности электрического тока 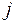
В. К статической электродинамике относят и процессы протекания постоянных токов в распределенных проводящих средах. В этом случае справедлива система уравнений (104.2), где вместо третьего уравнения записано 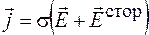
2. 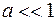
Все квазистационарные поля и процессы можно разделить на две группы. К первой принадлежат квазистационарные системы, в которых электрические и магнитные поля пространственно разнесены. Простейшим примером является колебательный контур, в котором магнитное поле сосредоточено в основном в катушке самоиндукции, а электрическое – в конденсаторе. Сюда же относятся и некоторые цепи переменного тока и переходные процессы в электрических цепях. Цепи с приближенно разнесенными электрическим и магнитным полями относят к системам с сосредоточенными параметрами.
Критерием медленности изменения поля в таких системах служит условие
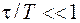
где 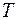
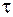
Соотношение (104.4) – условие квазистационарности тока – реально выполняется только в макроскопических системах. Квазистационарное магнитное поле качественно отличается от стационарного электрического. Это различие между электрическими и магнитными полями обусловлено явлением электромагнитной индукции, согласно которому переменное магнитное поле порождает электрическое поле, линии которого замкнуты. Поэтому квазистационарное электрическое поле не является потенциальным, оно всегда вихревое.
Вторая группа квазистационарных систем включает системы с неразделенными электрическим и магнитным полями. Примером таких объектов могут служить хорошо проводящие среды, токи проводимости в которых существенно больше токов смещения. Для таких систем характерны эффекты прижатия полей к поверхностям раздела проводник–диэлектрик (скин-эффект), наведение внешними полями вихревых токов в массивных проводниках (токи Фуко) и т. п.
Квазистационарные процессы подчиняются следующим уравнениям Максвелла:
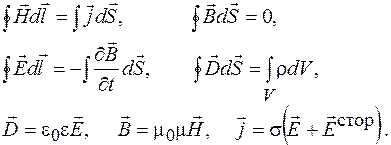
Критерием квазистационарности таких процессов является малость токов смещения по сравнению с токами проводимости:
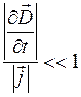
Для получения числовой оценки рассмотрим наиболее часто встречающийся случай, когда через среду проходит электромагнитная волна, вектор напряженности 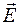
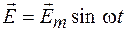
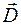
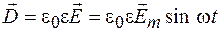
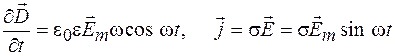
В результате для амплитудных значений получим:
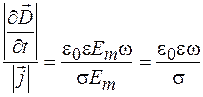
Здесь 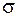
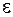
Таким образом, из выражения (104.7) в соответствии с выражением (104.6) следует, что условие квазистационарности электромагнитного поля можно представить в виде
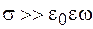
Отсюда следует, что условие (104.8) выполняется тем лучше, чем больше электропроводность вещества и меньше частота изменения поля. Так, например, положив для меди 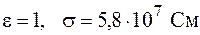
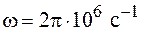
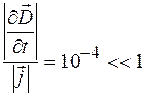
Таким образом, условие квазистационарности довольно хорошо выполняется для тонких (десятые доли миллиметра) проводников вплоть до дециметрового диапазона радиоволн. При более высоких частотах проводимость падает за счет скин-эффекта (см. формулу (105.5)) и справедливость условия (104.8) нарушается.
1. Резонансные волновые поля описываются полной системой уравнений Максвелла. Из общего класса полей выделяются поля, возбуждаемые внутри полых волноводов либо в окрестности тонкой проволочной или щелевой антенны. При этом поля представляются дискретным набором колебаний.
4. 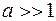
В заключение заметим, что квазистационарное приближение реализуется для полей любой физической природы: акустических, гравитационных и т. д. Критерием такого приближения, как и в случае электромагнитных систем, является малость параметра 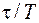
🔥 Видео
Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

ЧК_МИФ /ЛИКБЕЗ/ 3_3_5_1 СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА. ПРИМЕРЫ (минимум теории)Скачать

Уравнения Максвелла Лекция 10-1Скачать

Уравнения Максвелла в вакууме. Потенциалы электромагнитного поля.Скачать

3 14 Уравнения МаксвеллаСкачать

Лекция №9. Уравнения МаксвеллаСкачать

Электродинамика | уравнения Максвелла | 1 | для взрослыхСкачать
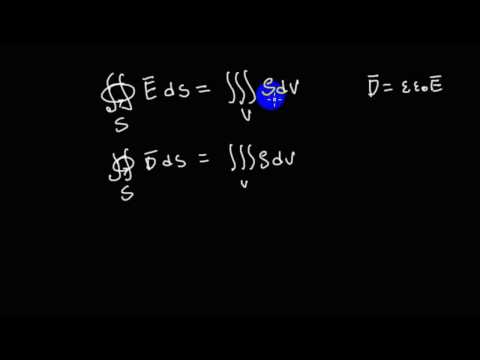
Уравнения Максвелла — Мартин МакколлСкачать

7. Ограниченность уравнений Максвелла. Уточнения уравнений электродинамики. Ацюковский В.А.Скачать

1.1. Решение системы уравнений Максвелла методом интегральных преобразованийСкачать

Система уравнений Максвелла. Связь интегральной и дифференциальной формы уравнений.Скачать

Уравнения Максвелла 2021Скачать

Электромагнитные волны и уравнения Максвелла — Эмиль АхмедовСкачать

Урок 284. Задачи на электромагнитную индукцию - 1Скачать