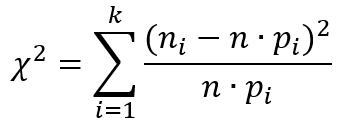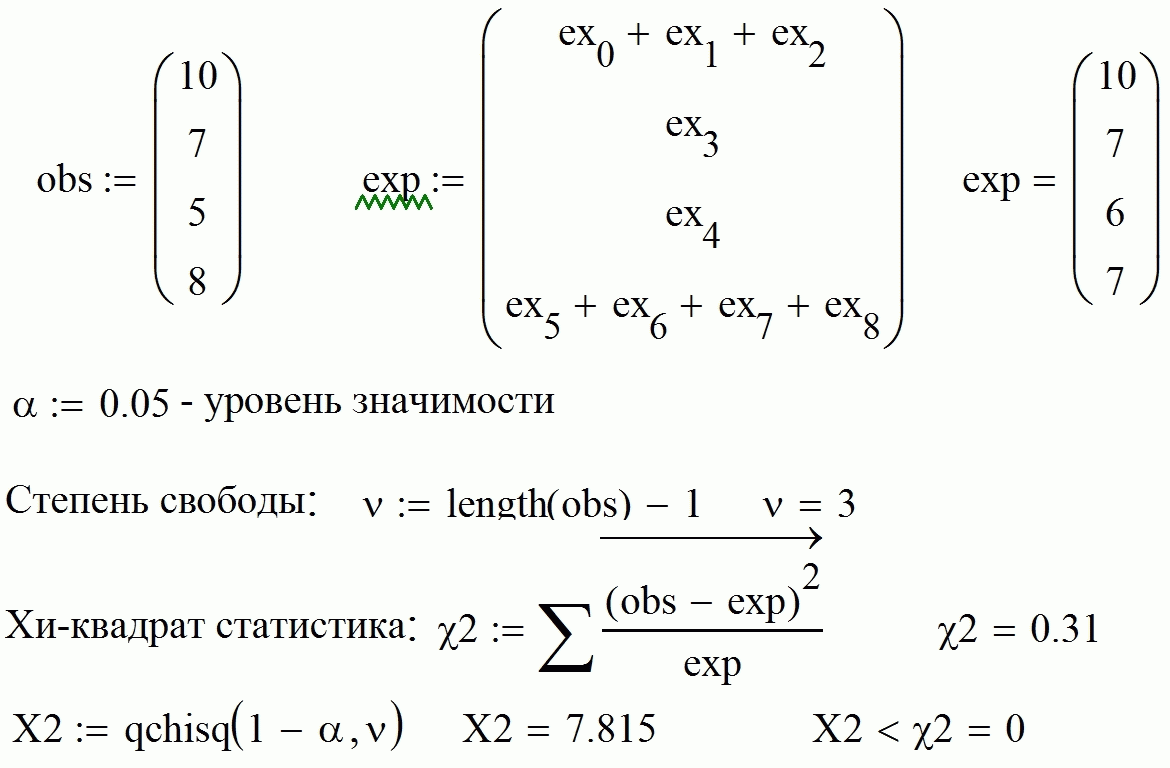Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Задание
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 2 | 3 | 4 | 6 | 4 | 3 | |
| 5 | 4 | 2 | 1 | 4 | 5 | 3 |
| 4 | 5 | 3 | 5 | 8 | 2 | 2 |
| 3 | 1 | 3 | 6 | 2 | 1 | 3 |
| 2 | 7 | 1 |
П риняв уровень значимости alpha=0.05, проверить согласие этих данных обычного месяца с распределением Пуассона, пользуясь критерием Хи-квадрат. Перепроверить данные с помощью критерия Колмогорова-Смирнова, по прежнему принимая alpha =0.05.
Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Методические указания
Критерий Хи-квадрат предпочтителен, когда исследуются большие объемы выборок. При малых объемах выборок этот критерий практически не пригоден.
Нулевая гипотеза при применении общих критериев согласия записывается в форме
где Fn(x) – эмпирическая функция распределения вероятностей; F(x) – гипотетическая функция распределения вероятностей.
Критерий Пирсона X 2 основан на сравнении эмпирической гистограммы распределения случайной величины с ее теоретической плотностью. Диапазон изменения экспериментальных данных разбивается на k интервалов, и подсчитывается статистика:
где ni – количество значений случайной величины, попавших в i-й интервал; n – объем выборки; F(x) – гипотетический теоретический закон распределения вероятностей случайной величины; pi = F(xi+1) — F(xi) – теоретическая вероятность попадания случайной величины в i-й интервал.
Статистика X 2 имеет распределение Хи-квадрат с f = n — 1 степенями свободы в том случае, когда проверяется простая нулевая гипотеза H0, т.е., когда гипотетическое распределение, на соответствие которому проверяется эмпирический ряд данных, известно с точностью до значения своих параметров.
Правило проверки гипотезы:
то на уровне значимости alpha, т. е. с достоверностью (1 — alpha) гипотеза
На мощность статистического критерия X 2 сильное влияние оказывает чиcло интервалов разбиения гистограммы (k) и порядок ее разбиения (т. е. выбор длин интервалов внутри диапазона изменения значений случайной величины). На практике принято считать, что статистику X 2 можно использовать, когда npi >= 5.
Такое приближение допустимо и тогда, когда не более, чем в 20% интервалов имеет место 1 k = 1+ 3,32·lg n
При n >= 200 можно выбирать k из условия
Еще одно простое правило: выбрать как можно большее k, но не превышающее n/5:
Критерий Крамера-фон Мизеса дает хорошие результаты при малых объемах выборок (менее 10). Однако вопрос о доверительной вероятности остается нерешенным (эта вероятность мала при значительных размерах доверительных интервалов.
Исходя из этого, полагают, что реальные объемы выборок, которые можно получить, находятся в диапазоне от 10 до 100.
Критерий Колмогорова-Смирнова также целесообразно использовать для выборки указанных объемов в тех случаях, когда проверяемое распределение непрерывно и известны среднее значение и дисперсия проверяемой совокупности.
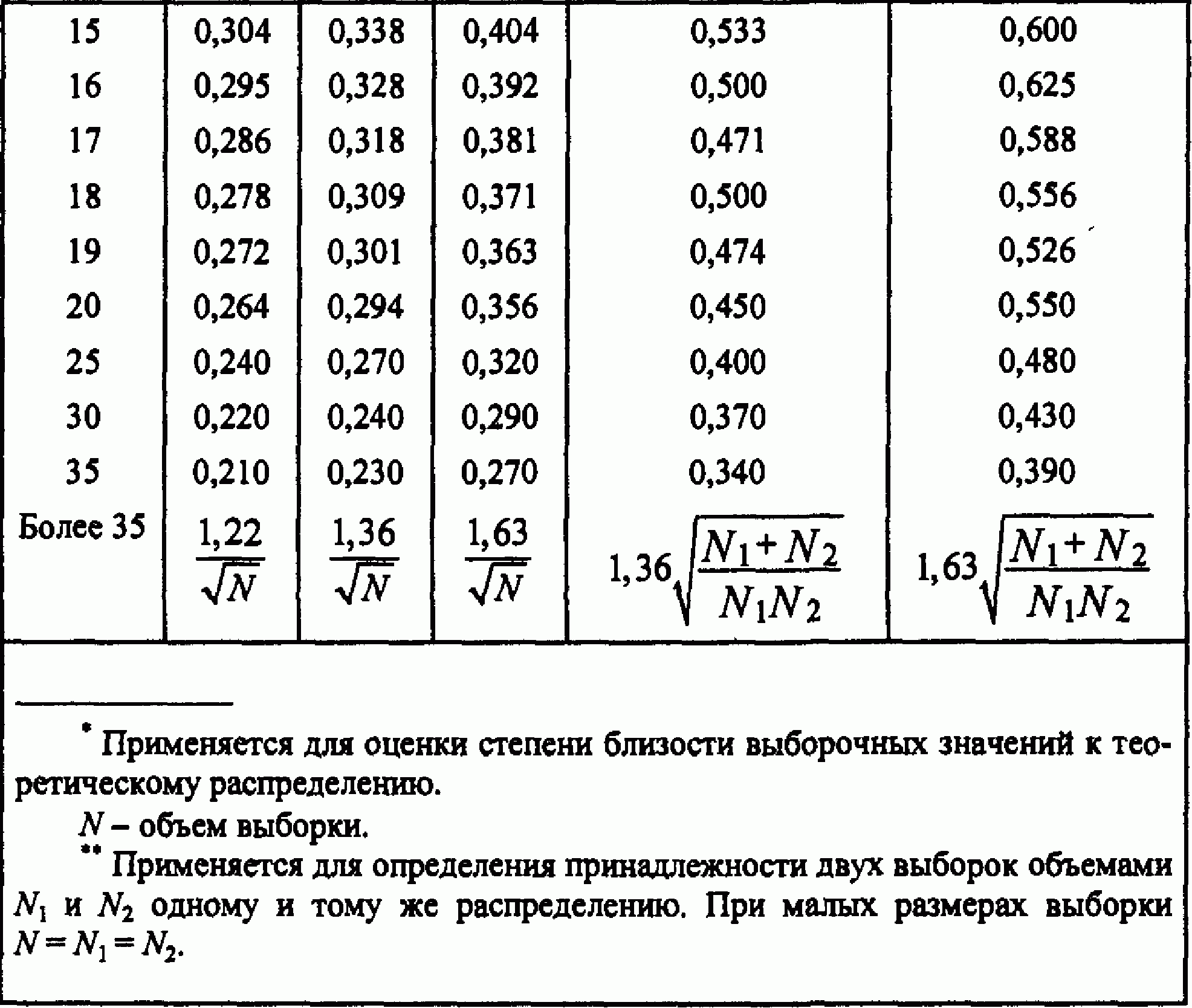
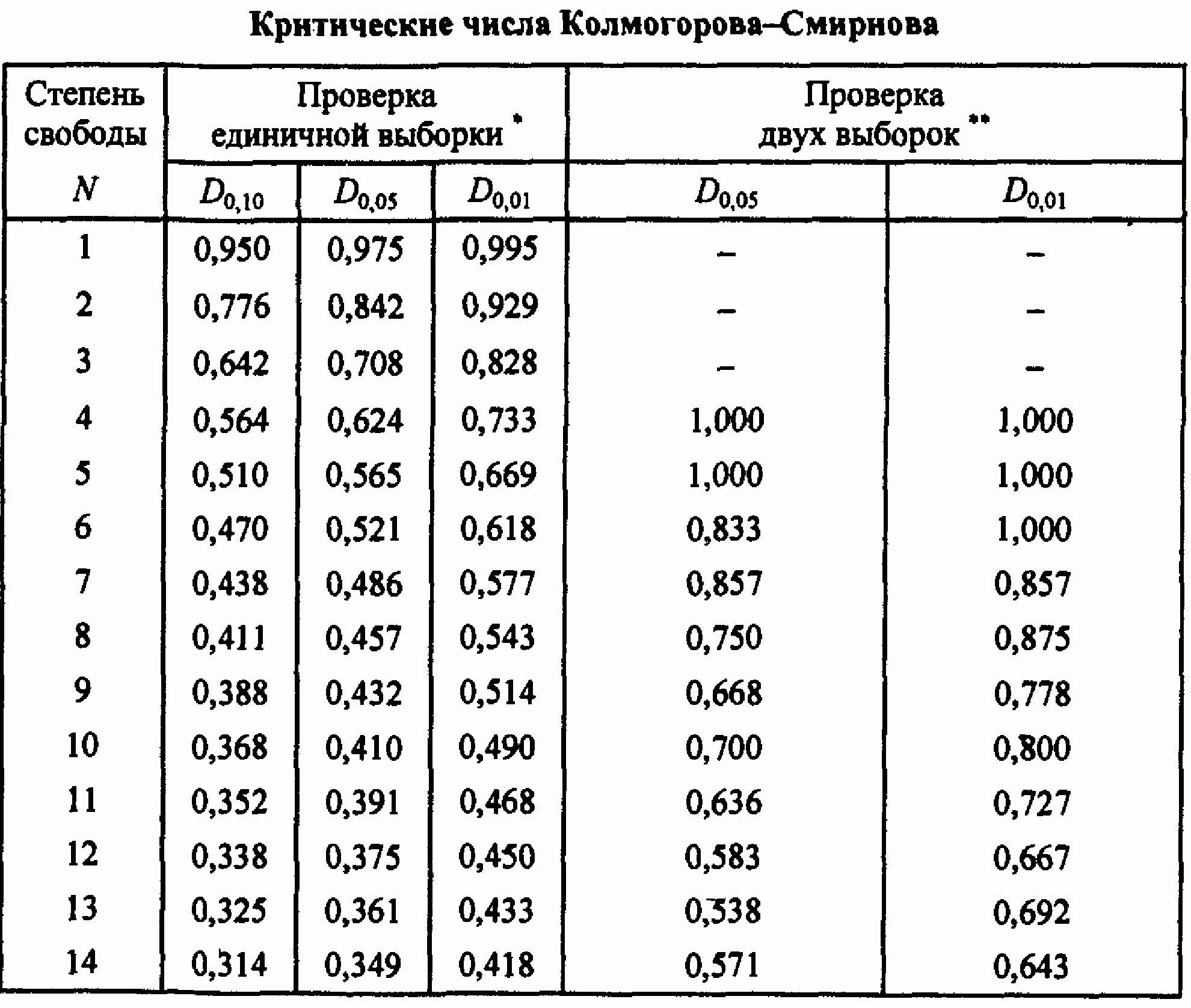
Алгоритм реализации критерия Колмогорова-Смирнова предполагает использование критического значения D extr для проверки принятой гипотезы. Для этого используется приведенная ниже табл. 1.
Видео:Решение уравнений с помощью ExcelСкачать

Решение
1. Критерий Хи-квадрат
1.1. Реализация в MathCad

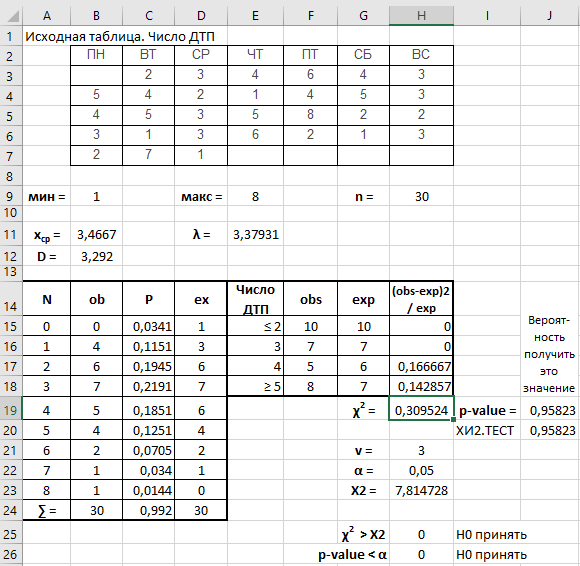
1.2. Реализация в Excel
Формулы ячеек на листе Excel представлены в табл. 2.
| Ячейка | Характеристика | Формула |
| В15 | – число случаев исхода | =СЧЁТЕСЛИ($B$3:$H$7;A15) |
| С15 | – вероятность наступления | =ПУАССОН.РАСП(A15;$E$11;ЛОЖЬ) |
| D15 | – ожидаемое число случаев исхода | =ОКРУГЛ(C15*$H$9;0) |
| H19 | – статистика Хи-квадрат | =СУММ(H15:H18) |
| H23 | – критическое значение Хи-квадрата (максимальное значение для заданного уровня значимости) | =ХИ2.ОБР(1-H22;H21) |
| J19 | – p-value (вероятность получить расчетное значение Хи-квадрата) | =ХИ2.РАСП.ПХ(H19;H21) |
| J20 | – Хи-квадрат тест | =ХИ2.ТЕСТ(F15:F18;G15:G18) |
2. Критерий Колмогорова-Смирнова
Литература
- Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов: уч. пособ. — М.: Финансы и статистика, 2002. — 368с.
- Кобзарь А. И. Прикладная математическая статистика. Для инженеров и научных работников. — М.: ФИЗМАТЛИТ, 2006. — 816 с.
© В.Н. Кравченко
Последнее обновление: 2018.11.03
Видео:Решить простейшее уравнение. MS Excel. Подбор параметраСкачать

Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Видео:Численное решение уравнений, урок 2/5. Метод деления отрезка пополамСкачать

Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Видео:Матрица интенсивностей. Система уравнений КолмогороваСкачать

Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Видео:решаем квадратные уравнения в ExcelСкачать

Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Видео:Решить квадратное уравнение. MS Excel. Поиск решенияСкачать

Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Видео:Excel Подбор параметра. Решение математических уравненийСкачать

Уравнения Колмогорова.
Предельные вероятности состояний
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .
Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:
Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.
1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:
2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .
Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).
Применяя теорему сложения вероятностей, получим
Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:
Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:
Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при
Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или
(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).
Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)
Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).
Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен
Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:
Решив систему, получим .
Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:
Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.
Видео:10-09 Критерий КолмогороваСкачать

Процесс гибели и размножения
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.
Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .
По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния
для состояния имеем , которое с учетом (12) приводится к виду
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
к которой добавляется нормировочное условие
При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.
Решая систему (14), (15), можно получить
Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .
Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.
🎦 Видео
Метод Крамера для решения систем линейных алгебраических уравнений (СЛАУ) в ExcelСкачать

Численное решение уравнений, урок 3/5. Метод хордСкачать

Решение уравнения теплопроводности методом конечных разностейСкачать

Численный метод Ньютона в ExcelСкачать

Решение систем линейных уравнений, урок 4/5. Метод ГауссаСкачать

Метод ЭйлераСкачать

Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательныхСкачать

Решение системы нелинейных уравнений графическим способом средствами ExcelСкачать

Решение системы уравнений Колмогорова в МатлабеСкачать

Численные методы решения интегралов в MS ExcelСкачать