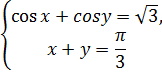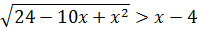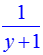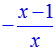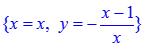Решение обыкновенных уравнений.
Для решения уравнений в Maple существует универсальная команда solve(eq,x) , где eq – уравнение, x – переменная, относительно которой уравнение надо разрешить. В результате выполнения этой команды в строке вывода появится выражение, которое является решением данного уравнения. Например:
Если уравнение имеет несколько решений, которые вам понадобятся для дальнейших расчетов, то команде solve следует присвоить какое-нибудь имя name . Обращение к какому-либо k –ому решению данного уравнения производится указанием его имени с номером решения k в квадратных скобках: name[k] . Например:
Решение систем уравнений.
Системы уравнений решаются с помощью такой же команды solve(,) , только теперь в параметрах команды следует указывать в первых фигурных скобках через запятую уравнения, а во вторых фигурных скобках перечисляются через запятую переменные, относительно которых требуется решить систему. Если вам будет необходимо для дальнейших вычислений использовать полученные решения уравнений, то команде solve следует присвоить какое-нибудь имя name . Затем выполняется присвоения команда assign(name) . После этого над решениями можно будет производить математические операции. Например:
Численное решение уравнений.
Для численного решения уравнений, в тех случаях, когда трансцендентные уравнения не имеют аналитических решений, используется специальная команда fsolve(eq,x) , параметры которой такие же, как и команды solve . Например:
Решение рекуррентных и функциональных уравнений.
Команда rsolve(eq,f) позволяет решить рекуррентное уравнение eq для целой функции f . Можно задать некоторое начальное условие для функции f(n) , тогда получиться частное решение данного рекуррентного уравнения. Например:
Универсальная команда solve позволяет решать функциональные уравнения, например:
F := proc ( x ) RootOf(_ Z ^2 — 3*_ Z + 2* x ) end
В результате получается решение в неявном виде. Однако Maple может работать с такими решениями. Неявное решение функционального уравнения можно попытаться преобразовать в какую-либо элементарную функцию с помощью команды convert . Продолжая приведенный выше пример, можно получить решение в явном виде:
Решение тригонометрических уравнений.
Команда solve , примененная для решения тригонометрического уравнения, выдает только главные решения, то есть решения в интервале [0,2 p ]. Для того, чтобы получить все решения, следует предварительно ввести дополнительную команду _EnvAllSolutions:=true. Например:
В Maple символ _ Z
обозначает константу целого типа, поэтому решение данного уравнения в привычной форме имеет вид 
, где n – целые числа.
Решение трансцендентных уравнений.
При решении трансцендентных уравнений для получения решения в явном виде перед командой solve следует ввести дополнительную команду _EnvExplicit:=true . Пример решения сложной системы трансцендентных уравнений и упрощения вида решений:
Видео:Вычисления, константы и решение уравнений в MapleСкачать
Решение уравнений и неравенств. В Maple 14 имеется встроенная функция solve(уравнение или неравенство, переменная), предназначенная для решения уравнений и неравенств
В Maple 14 имеется встроенная функция solve(уравнение или неравенство, переменная), предназначенная для решения уравнений и неравенств. Если уравнение или неравенство имеет одну переменную, то имя переменной в функции можно опустить.
Например, необходимо решить алгебраическое уравнение
Для этого вводим уравнение:
Уравнение набрано верно. С помощью функции solve() решаем уравнение:
Решим следующее уравнение с параметрами
Поскольку переменных несколько, то необходимо указать переменную х, относительно которой решается уравнение:
Получили два корня: 
Проверку правильности решения можно осуществить встроенной функцией subs(), которая вычисляет значение выражения. Функция subs(x = a, f) имеет несколько аргументов, где х — переменная в выражении f; а — значение переменной х.
Например, решаем уравнение
> solve(5*x^2 + abs(x+7) — 13 = 0);
> subs(x = 1, 5*х^2 + abs(x + 7) — 13 = 0);
>subs(x = -6/5, 5*х^2 + abs(x + 7) — 13 = 0);
Решим иррациональное уравнение
С помощью функции solve() можно решать системы уравнений, при этом уравнения и неизвестные указываются в фигурных скобках через запятую [1]. Например, необходимо решить систему уравнений
Решение будет следующим:
Действительных решений системы уравнений два: (2, 1) и (1, 2).
Для тригонометрического уравнения функция solve() по умолчанию возвращает только один корень. Для возвращения множества корней необходимо использовать необязательный аргумент AUSolutions. Например,
Форма ответа здесь необычная, однако корни уравнения найдены правильно. Переменная _В, независимо от индекса, принимает значения из множества , а значения Z принадлежат множеству целях чисел. Таким образом, полученное множество корней уравнения можно представить в виде
и записать в привычной форме
Решим тригонометрическое уравнение
3sin 2 2х + 7cos2x — 3 = 0.
Решим систему тригонометрических уравнений
Ответ: 
Теперь рассмотрим решение неравенств и систем неравенств. Например, решим иррациональное неравенство
>solve(sqrt(24 — 10х + х*х) > х — 4);
RealRange(- 
>solve( 
)
Ответ: ( 0,1/2) 
(l,2) (3,6).
Контрольные вопросы
1. В каком порядке выполняются арифметические операции?
2. Каково назначение скобок при записи выражений?
3. Как записать степень числа в программе Maple?
4. Какое назначение имеет ! (восклицательный знак) на панели инструментов?
5. Как преобразовать градусы в радианы?
6. Как получить числовое значение функции?
7. Как вычислить натуральный логарифм числа?
8. Как получить приближенное значение действительного числа в Maple (c заданным числом значащих цифр)?
9. Какой командой осуществляется вызов библиотеки подпрограмм?
10. Какие функции преобразования математических выражений вы знаете?
11. Как упростить иррациональное число?
12. Как осуществить подстановку в выражении?
13. Как при преобразовании выражения указать диапазон изменения переменной?
14. Как с помощью функции solve()получить множество решений для тригонометрических уравнений?
Контрольные задания
1. Оформите титульный лист к лабораторной работе, согласно требованиям СФМЭИ (ТУ). Укажите название лабораторной работы. Фамилию, Имя, группу, номер студента в журнале (см. Приложение 1).
2. Создайте документ Maple. Напишите заголовок 14 кеглем, полужирно, с выравниванием по центру: «Лабораторная работа №1». Далее с выравниванием по правому краю, курсивом, 14 кеглем укажите полностью Фамилию, Имя, номер в журнале.
3. Выполните задания из своего варианта, определяемого номером в журнале. Каждое задание должно быть оформлено в отдельной секции (пиктограммы 
) с заголовком «Задание №_». Завершать секцию должен развернутый ответ.
4. Распечатайте лабораторную работу из под программы Maple на листах формата А4 (односторонняя печать).
При выполнении контрольных заданий студенту необходимо подставить вместо буквенных параметров индивидуальные анкетные характеристики:
— число букв в фамилии студента,
— число букв в полном имени студента,
— номер студента по списку в журнале.
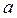
В отчете на титульном листе необходимо обязательно указать, какие анкетные данные использовались при выполнении контрольных заданий (имя, фамилия, номер варианта).
Видео:Решение системы линейных уравнений в MapleСкачать
Maple. Решение алгебраических задач. Решения уравнений, систем уравнений и неравенств в Maple
Страницы работы
Содержание работы
Решение алгебраических задач
Решение уравнений (часть 1)
Для решения уравнений, систем уравнений и неравенств в Maple используется команда (оператор) «solve». Например, для решения уравнения х2 – 6х + 5 = 0 набираем: > solve(x^2–6*x+5=0); 1, 5 Обратите внимание, что если аргумент solve не является уравнением (или неравенством), то Maple трактует его так, как если бы это выражение было приравнено к 0. Можно было бы написать «> solve(x^2–6*x+5);». При решении алгебраических уравнений Maple приводит все корни, включая комплексные: > solve(x^4=1); 1, –1, I, –I
Решение уравнений (часть 2)
С помощью команды «solve» можно решать не только алгебраические уравнения. Например, решим тригоно-метрическое уравнение tg x – 2 sin x = 0: > solve(tan(x)–2*sin(x)); Обратите внимание, что Maple привёл решения, лежащие в пределах одного промежутка периодичности (от –π до π). Для вывода всех решений необходимо присвоить зарезервированной переменной _EnvAllSolutions значение true: > _EnvAllSolutions := true; > solve(tan(x)–2*sin(x)); где _Z
обозначает любое целое число.
Решение уравнений (часть 3)
Приведём примеры применения функции «solve» для решения уравнений с несколькими переменными. Решим, например, уравнение xy + x – 1 = 0 относительно x: > solve(x*y+x–1,x); относительно y: > solve(x*y+x–1,у); В общем виде Maple решает это уравнение так: > solve(x*y+x–1); Видно, что форма ответа определяется вторым параметром (или его отсутствием) команды «solve», указывающим, относительно какой переменной решать уравнение.
Неравенства решаются тем же оператором «solve». Например, решим неравенство x2(x – 1) solve(x^2*(x–1) solve(x^2*(x–1)>=0); 0, RealRange(1, ∞) В переводе на математический язык ответ: U[1; ∞). Открытый интервал (или луч) задаётся в Maple с помощью функции «Open», применяемой к концам интервала, задаваемого функцией «RealRange».
Решение системы уравнений
Все уравнения системы записываются в фигурных скобках через запятую. Решим например систему > solve(); , Решим систему с параметром > solve(,);
🎦 Видео
Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать
Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать
Как решать неравенства? Часть 1| МатематикаСкачать
Решение системы неравенствСкачать
Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать
Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать
РЕШЕНИЕ ВОЛНОВОГО ДУ ОПЕРАЦИОННЫМ МЕТОДОМ В СРЕДЕ MAPLESOFT MAPLE 2017Скачать
Решение системы неравенств с двумя переменными. 9 класс.Скачать
Графики, функции, решение системы линейных уравнений в MapleСкачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Неравенства с модулем | Математика | TutorOnlineСкачать
Неравенства с модулем. Как правильно раскрывать модульСкачать
Контрольная работа. Уравнения с МОДУЛЕМСкачать
Начало работы с Maple 2017 | Getting Started with Maple 2017Скачать
Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать
11 класс, 29 урок, Уравнения и неравенства с модулямиСкачать
Интерактивная математика в Maple 2017 | Clickable Math in Maple 2017Скачать
Решение систем уравнений методом подстановкиСкачать
