Решение уравнений и неравенств с помощью графиков (5 видео)

Решение квадратных неравенств графически

Графический метод является одним из основных методов решения квадратных неравенств. В статье мы приведем алгоритм применения графического метода, а затем рассмотрим частные случаи на примерах.

Содержание

Суть графического метода
Решение с двумя корнями у квадратного трехчлена
Решение с одним корнем у квадратного трехчлена
Решение квадратного трехчлена, не имеющего корней
Алгоритм решения неравенств с использованием графического способа
Реферат » Решение уравнений и неравенств графическим способом» ( 9 класс)
Графическое решение уравнений, неравенств
📸 Видео

Видео:Применение графиков к решению линейных неравенств.Скачать

Суть графического метода

Метод применим для решения любых неравенств, не только квадратных. Суть его вот в чем: правую и левую части неравенства рассматривают как две отдельные функции y = f ( x ) и y = g ( x ) , их графики строят в прямоугольной системе координат и смотрят, какой из графиков располагается выше другого, и на каких промежутках. Оцениваются промежутки следующим образом:

решениями неравенства f ( x ) > g ( x ) являются интервалы, где график функции f выше графика функции g ;
решениями неравенства f ( x ) ≥ g ( x ) являются интервалы, где график функции f не ниже графика функции g ;
решениями неравенства f ( x ) g ( x ) являются интервалы, где график функции f ниже графика функции g ;
решениями неравенства f ( x ) ≤ g ( x ) являются интервалы, где график функции f не выше графика функции g ;
абсциссы точек пересечения графиков функций f и g являются решениями уравнения f ( x ) = g ( x ) .

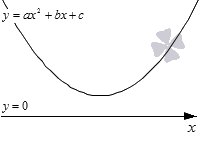
Рассмотрим приведенный выше алгоритм на примере. Для этого возьмем квадратное неравенство a · x 2 + b · x + c 0 ( ≤ , > , ≥ ) и выведем из него две функции. Левая часть неравенства будет отвечать y = a · x 2 + b · x + c (при этом f ( x ) = a · x 2 + b · x + c ) , а правая y = 0 (при этом g ( x ) = 0 ).

Графиком первой функции является парабола, второй прямая линия, которая совпадает с осью абсцисс О х . Проанализируем положение параболы относительно оси О х . Для этого выполним схематический рисунок.

Видео:Графический способ решения уравнений и неравенств | Алгебра 10 классСкачать

Решение с двумя корнями у квадратного трехчлена

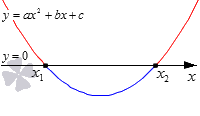
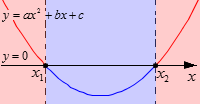
Ветви параболы направлены вверх. Она пересекает ось О х в точках x 1 и x 2 . Коэффициент а в данном случае положительный, так как именно он отвечает за направление ветвей параболы. Дискриминант положителен, что указывает на наличие двух корней у квадратного трехчлена a · x 2 + b · x + c . Корни трехчлена мы обозначили как x 1 и x 2 , причем приняли, что x 1 x 2 , так как на оси О х изобразили точку с абсциссой x 1 левее точки с абсциссой x 2 .

Части параболы, расположенные выше оси О х обозначим красным, ниже – синим. Это позволит нам сделать рисунок более наглядным.

Выделим промежутки, которые соответствуют этим частям и отметим их на рисунке полями определенного цвета.

Красным мы отметили промежутки ( − ∞ , x 1 ) и ( x 2 , + ∞ ) , на них парабола выше оси О х . Они являются решением квадратного неравенства a · x 2 + b · x + c > 0 . Синим мы отметили промежуток ( x 1 , x 2 ) , который является решением неравенства a · x 2 + b · x + c 0 . Числа x 1 и x 2 будут отвечать равенству a · x 2 + b · x + c = 0 .

Сделаем краткую запись решения. При a > 0 и D = b 2 − 4 · a · c > 0 (или D ‘ = D 4 > 0 при четном коэффициенте b ) мы получаем:

решением квадратного неравенства a · x 2 + b · x + c > 0 является ( − ∞ , x 1 ) ∪ ( x 2 , + ∞ ) или в другой записи x x 1 , x > x 2 ;
решением квадратного неравенства a · x 2 + b · x + c ≥ 0 является ( − ∞ , x 1 ] ∪ [ x 2 , + ∞ ) или в другой записи x ≤ x 1 , x ≥ x 2 ;
решением квадратного неравенства a · x 2 + b · x + c 0 является ( x 1 , x 2 ) или в другой записи x 1 x x 2 ;
решением квадратного неравенства a · x 2 + b · x + c ≤ 0 является [ x 1 , x 2 ] или в другой записи x 1 ≤ x ≤ x 2 ,

где x 1 и x 2 – корни квадратного трехчлена a · x 2 + b · x + c , причем x 1 x 2 .

Видео:Решение квадратных неравенств графическим методом. 8 класс.Скачать

Решение с одним корнем у квадратного трехчлена

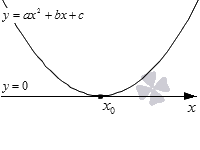
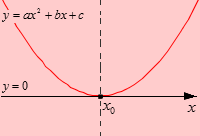
На данном рисунке парабола касается оси O х только в одной точке, которая обозначена как x 0 . Ветви параболы направлены вверх, что означает, что a > 0 . D = 0 , следовательно, квадратный трехчлен имеет один корень x 0 .

Парабола расположена выше оси O х полностью, за исключением точки касания координатной оси. Обозначим цветом промежутки ( − ∞ , x 0 ) , ( x 0 , ∞ ) .

Запишем результаты. При a > 0 и D = 0 :

решением квадратного неравенства a · x 2 + b · x + c > 0 является ( − ∞ , x 0 ) ∪ ( x 0 , + ∞ ) или в другой записи x ≠ x 0 ;
решением квадратного неравенства a · x 2 + b · x + c ≥ 0 является ( − ∞ , + ∞ ) или в другой записи x ∈ R ;
квадратное неравенство a · x 2 + b · x + c 0 не имеет решений (нет интервалов, на которых парабола расположена ниже оси O x );
квадратное неравенство a · x 2 + b · x + c ≤ 0 имеет единственное решение x = x 0 (его дает точка касания),

где x 0 — корень квадратного трехчлена a · x 2 + b · x + c .

Видео:Графический метод решения показательных уравнений и неравенств Алгебра 10 (база)Скачать

Решение квадратного трехчлена, не имеющего корней

Рассмотрим третий случай, когда ветви параболы направлены вверх и не касаются оси O x . Ветви параболы направлены вверх, что означает, что a > 0 . Квадратный трехчлен не имеет действительных корней, так как D 0 .

На графике нет интервалов, на которых парабола была бы ниже оси абсцисс. Это мы будем учитывать при выборе цвета для нашего рисунка.

Получается, что при a > 0 и D 0 решением квадратных неравенств a · x 2 + b · x + c > 0 и a · x 2 + b · x + c ≥ 0 является множество всех действительных чисел, а неравенства a · x 2 + b · x + c 0 и a · x 2 + b · x + c ≤ 0 не имеют решений.

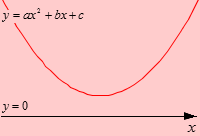
Нам осталось рассмотреть три варианта, когда ветви параболы направлены вниз. На этих трех вариантах можно не останавливаться подробно, так как при умножении обеих частей неравенства на − 1 мы получаем равносильное неравенство с положительным коэффициентом при х 2 .

Видео:Решение неравенств с помощью графиковСкачать

Алгоритм решения неравенств с использованием графического способа

Рассмотрение предыдущего раздела статьи подготовило нас к восприятию алгоритма решения неравенств с использованием графического способа. Для проведения вычислений нам необходимо будет каждый раз использовать чертеж, на котором будет изображена координатная прямая O х и парабола, которая отвечает квадратичной функции y = a · x 2 + b · x + c . Ось O у мы в большинстве случаев изображать не будем, так как для вычислений она не нужна и будет лишь перегружать чертеж.

Для построения параболы нам необходимо будет знать две вещи:

направление ветвей, которое определяется значением коэффициента a ;
наличие точек пересечения параболы и оси абсцисс, которые определяются значением дискриминанта квадратного трехчлена a · x 2 + b · x + c .

Точки пересечения и касания мы будет обозначать обычным способом при решении нестрогих неравенств и пустыми при решении строгих.

Наличие готового чертежа позволяет перейти к следующему шагу решения. Он предполагает определение промежутков, на которых парабола располагается выше или ниже оси O х . Промежутки и точки пересечения и являются решением квадратного неравенства. Если точек пересечения или касания нет и нет интервалов, то считается, что заданное в условиях задачи неравенство не имеет решений.

Теперь решим несколько квадратных неравенств, используя приведенный выше алгоритм.

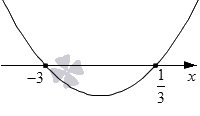
Необходимо решить неравенство 2 · x 2 + 5 1 3 · x — 2 графическим способом.

Решение

Нарисуем график квадратичной функции y = 2 · x 2 + 5 1 3 · x — 2 . Коэффициент при x 2 положительный, так как равен 2 . Это значит, что ветви параболы будут направлены вверх.

Вычислим дискриминант квадратного трехчлена 2 · x 2 + 5 1 3 · x — 2 для того, чтобы выяснить, имеет ли парабола с осью абсцисс общие точки. Получаем:

D = 5 1 3 2 — 4 · 2 · ( — 2 ) = 400 9

Как видим, D больше нуля, следовательно, у нас есть две точки пересечения: x 1 = — 5 1 3 — 400 9 2 · 2 и x 2 = — 5 1 3 + 400 9 2 · 2 , то есть, x 1 = − 3 и x 2 = 1 3 .

Мы решаем нестрогое неравенство, следовательно проставляем на графике обычные точки. Рисуем параболу. Как видите, рисунок имеет такой же вид как и в первом рассмотренном нами шаблоне.

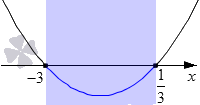
Наше неравенство имеет знак ≤ . Следовательно, нам нужно выделить промежутки на графике, на которых парабола расположена ниже оси O x и добавить к ним точки пересечения.

Нужный нам интервал − 3 , 1 3 . Добавляем к нему точки пересечения и получаем числовой отрезок − 3 , 1 3 . Это и есть решение нашей задачи. Записать ответ можно в виде двойного неравенства: − 3 ≤ x ≤ 1 3 .

Ответ: − 3 , 1 3 или − 3 ≤ x ≤ 1 3 .

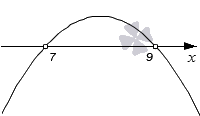
Решите квадратное неравенство − x 2 + 16 · x − 63 0 графическим методом.

Решение

Квадрат переменной имеет отрицательный числовой коэффициент, поэтому ветви параболы будут направлены вниз. Вычислим четвертую часть дискриминанта D ‘ = 8 2 − ( − 1 ) · ( − 63 ) = 64 − 63 = 1 . Такой результат подсказывает нам, что точек пересечения будет две.

Вычислим корни квадратного трехчлена: x 1 = — 8 + 1 — 1 и x 2 = — 8 — 1 — 1 , x 1 = 7 и x 2 = 9 .

Получается, что парабола пересекает ось абсцисс в точках 7 и 9 . Отметим эти точки на графике пустыми, так как мы работаем со строгим неравенством. После этого нарисуем параболу, которая пересекает ось O х в отмеченных точках.

Нас будут интересовать промежутки, на которых парабола располагается ниже оси O х . Отметим эти интервалы синим цветом.

Получаем ответ: решением неравенства являются промежутки ( − ∞ , 7 ) , ( 9 , + ∞ ) .

Ответ: ( − ∞ , 7 ) ∪ ( 9 , + ∞ ) или в другой записи x 7 , x > 9 .

В тех случаях, когда дискриминант квадратного трехчлена равен нулю, необходимо внимательно подходить к вопросу о том, стоит ли включать в ответ абсциссы точки касания. Для того, чтобы принять правильное решение, необходимо учитывать знак неравенства. В строгих неравенствах точка касания оси абсцисс не является решением неравенства, в нестрогих является.

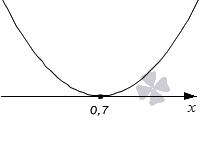
Решите квадратное неравенство 10 · x 2 − 14 · x + 4 , 9 ≤ 0 графическим методом.

Решение

Ветви параболы в данном случае будут направлены вверх. Она будет касаться оси O х в точке 0 , 7 , так как

Построим график функции y = 10 · x 2 − 14 · x + 4 , 9 . Ее ветви направлены вверх, так как коэффициент при x 2 положительный, и она касается оси абсцисс в точке с абсциссой 0 , 7 , так как D ‘ = ( − 7 ) 2 − 10 · 4 , 9 = 0 , откуда x 0 = 7 10 или 0 , 7 .

Поставим точку и нарисуем параболу.

Мы решаем нестрогое неравенство со знаком ≤ . Следовательно. Нас будут интересовать промежутки, на которых парабола располагается ниже оси абсцисс и точка касания. На рисунке нет интервалов, которые удовлетворяли бы нашим условиям. Есть лишь точка касания 0 , 7 . Это и есть искомое решение.

Ответ: Неравенство имеет только одно решение 0 , 7 .

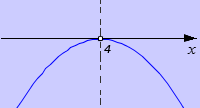
Решите квадратное неравенство – x 2 + 8 · x − 16 0 .

Решение

Ветви параболы направлены вниз. Дискриминант равен нулю. Точка пересечения x 0 = 4 .

Отмечаем точку касания на оси абсцисс и рисуем параболу.

Мы имеем дело со строгим неравенством. Следовательно, нас интересуют интервалы, на которых парабола расположена ниже оси O х . Отметим их синим.

Точка с абсциссой 4 не является решением, так как в ней парабола не расположена ниже оси O x . Следовательно, мы получаем два интервала ( − ∞ , 4 ) , ( 4 , + ∞ ) .

Ответ: ( − ∞ , 4 ) ∪ ( 4 , + ∞ ) или в другой записи x ≠ 4 .

Не всегда при отрицательном значении дискриминанта неравенство не будет иметь решений. Есть случаи, когда решением будет являться множество всех действительных чисел.

Решите квадратное неравенство 3 · x 2 + 1 > 0 графическим способом.

Решение

Коэффициент а положительный. Дискриминант отрицательный. Ветви параболы будут направлены вверх. Точек пересечения параболы с осью O х нет. Обратимся к рисунку.

Мы работаем со строгим неравенством, которое имеет знак > . Это значит, что нас интересуют промежутки, на которых парабола располагается выше оси абсцисс. Это как раз тот случай, когда ответом является множество всех действительный чисел.

Ответ: ( − ∞ , + ∞ ) или так x ∈ R .

Необходимо найти решение неравенства − 2 · x 2 − 7 · x − 12 ≥ 0 графическим способом.

Решение

Ветви параболы направлены вниз. Дискриминант отрицательный, следовательно, общих точек параболы и оси абсцисс нет. Обратимся к рисунку.

Мы работаем с нестрогим неравенством со знаком ≥ , следовательно, интерес для нас представляют промежутки, на которых парабола располагается выше оси абсцисс. Судя по графику, таких промежутков нет. Это значит, что данное у условии задачи неравенство не имеет решений.

Видео:Решение квадратных неравенств | МатематикаСкачать

Реферат » Решение уравнений и неравенств графическим способом» ( 9 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

МБОУ Алтайская СОШ №1

Тема : « Графическое решение уравнений и неравенств»

Учащаяся 9 а класса

МБОУ Алтайская СОШ №1

Бабаева Галина Яковлевна,

МБОУ Алтайской СОШ №1

С. Алтайское , Алтайский район, 2019 год.

II . Основная часть

2. Как графически решить уравнение________________________стр.4

3. Какие бывают функции ?________________________________стр.4

4. Графическое решение линейного уравнения с одной переменной.стр.5

5. Решение квадратного уравнения графическим способом._____ стр6-8

6. Графическое решение смешанных уравнений._______________стр.8-12. 7. Решение квадратных неравенств графическим способом_______стр.13

8. Решение линейных неравенств графическим способом стр 14

IV . Список литературы______________________________________стр.16

Цель моей работы – изложить графический метод решения уравнений и неравенств, который дает возможность определить корни или доказать ,что уравнение корней не имеет ( или решением неравенства является пустое множество).

Актуальность темы : графический метод, опирающийся на знания элементарных функций, удобно применять при решении задач на нахождение числа корней и на нахождение корней уравнений.

Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес. В данной исследовательской работе я показала как наиболее удобным способом преобразовывать уравнения . чтобы сводить к построению элементарных функций.

Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков не ограничивается только этим. В ряде случаев графики облегчают нахождение решений уравнений и неравенств, сокращая и упрощая аналитические выкладки, и часто при этом являются единственным методом решения таких задач. Данный метод может использоваться не только для одиночных уравнений, но и для их систем, а также неравенств

Уравнение – выражение, содержащее переменную.

Решить уравнение – это значит найти все его корни, или доказать, что их нет.

Корень уравнения – это число, при подстановке которого в уравнение получается верное числовое равенство.

График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргументов, а ординаты – соответствующим значениям функции.

Решение уравнений графическим способом позволяет найти точное или приближенное значение корней, позволяет найти количество корней уравнения.

При построении графиков и решении уравнений используются свойства функции, поэтому метод чаще называют функционально-графическим. Графиком функции y = f(x) называется множество всех точек координатной плоскости.

Заметим , что так как функция f сопоставляет каждому x D(f) одно число f(x) , то график функции f пересекается любой прямой, параллельной оси ординат, не более, чем в одной точке. И наоборот: всякое непустое множество точек плоскости, имеющее со всякой прямой, параллельной оси ординат, не более одной общей точки, является графиком некоторой функции.

Не всякое множество точек координатной плоскости является графиком какой-либо функции. Например, множество точек окружности не может быть графиком функции, поскольку значению абсциссы внутри окружности, соответствует два значения ординаты.

В общем случае уравнение с одной переменой х можно записать в виде f(x)=g(x),где f(x) и g(x) — некоторые функции. Функция f(x) является левой частью , а g(x) — правой частью уравнения.

Тогда для решения уравнения необходимо построить в одной системе координат графики функций f(x) и g(x). Абсциссы точек пересечения будут являться решениями данного уравнения.

Использование монотонности функций при решении уравнений: если функция строго возрастает, а функция строго убывает на некотором множестве, то графики этих функций имеют не более одной точки пересечения, а уравнение на этом множестве имеет не более одного решения. Поэтому, чтобы решить такие уравнения можно подобрать (если это удается) число, которое является их корнем.

2. Как графически решить уравнение.

Иногда уравнения решают графическим способом. Для этого надо преобразовать уравнение так (если оно уже не представлено в преобразованном виде), чтобы слева и справа от знака равенства стояли выражения, для которых легко можно нарисовать графики функций. Графическим решением уравнения являются абсциссы точек пересечения графиков построенных функций. Графики могут пересекаться в нескольких точках, в одной точке, вообще не пересекаться. Отсюда следует, что уравнение может иметь несколько корней, или один корень, или вообще их не иметь.

3. Какие бывают функции .

Линейная функция задаётся уравнением у = k*x+ b , где k и b – некоторые числа. Графиком этой функции является прямая. Для построения прямой достаточно в таблице значений взять только две точки. Это вытекает из аксиомы планиметрии

Функция обратной пропорциональности у =k/x , где. График этой функции называется гиперболой.

Функция (х– a)^2+ (у – b)^2 = r^2 , где а , b и r – некоторые числа. Это окружность радиуса r с центром в т. А ( а , b ).

Квадратичная функция y = a *х 2 + b*x+ c , где а, b, с – некоторые числа и

а не равно 0. Графиком этой функции является парабола.

Графики линейных функций, содержащих выражение под знаком модуля.

Для построения графиков функций, содержащих выражение под знаком модуля, сначала находят корни выражений, стоящих под знаком модуля. Эти корни разбивают числовую прямую на промежутки. График строят в каждом промежутке отдельно.

В простейшем случает, когда только одно выражение стоит под знаком модуля и нет слагаемых без знака модуля, можно построить график функций,

опустив знак модуля, а затем часть графика, расположенного в области отрицательных значений y , отобразить симметрично оси ОХ.

Элементарная функций, содержащая модуль :

4. Графическое решение линейного уравнения с одной переменной.

Как мы уже знаем, графиком линейного уравнения является прямая линия, отсюда и название данного вида. Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и уравнение решено. Мы нашли корень .А я покажу , как это сделать графическим способом.

Задание . Решить графическим способом уравнение : 2 x − 10 = 2

1)Перенесем слагаемые следующим образом: 2 x = 12.

2) Построим графики функций: y=2x и y=12.

Но можно решать и по-другому.

Для рассмотрения альтернативного решения вернемся к нашему уравнению:

Построим графики функций: y=2 x − 10 y =2

5. Решение квадратного уравнения графическим способом.

Для этого преобразуем уравнение к виду: х 2 =-2x+8 . Построим графики функций: у = -2x+8 и у = х 2

Получим точки пересечения графиков данных функций.

В ответ запишем абсциссы этих точек : x = -4 и x =2.

Данное уравнение можно решить , переписав уравнение следующим образом: x^2 – 8 = -2x

Тогда будем строить графики функций: y = x^2 – 8 и y = -2x.

А также уравнение можно решить , переписав следующим образом:

Тогда будем строить графики следующих функций : y = x^2 + 2x и y = 8 .

При этом абсциссы точек пересечения графиков будут одинаковые :

Задание. Решить уравнение: x² – 2x = 0

Перепишем уравнение в виде : x² = 2x

Построим графики функций y = x² и y = 2 и найдем точки их пересечения :

Задание. Решить уравнение: х 2 +2=0

Преобразуем так: х 2 = -2

Построим графики функций: у=-2 и у= х 2

Графики функций не пересекаются ,поэтому уравнение решений не имеет.

Ответ : решений нет.

6. Графическое решение смешанных уравнений.

Задание. Решить уравнение: 3/х +2 =х

1)Перенесем слагаемые таким образом: 3/ х = х-2

2) Построим графики функций от каждой части уравнения.

Найдем координаты точек пересечения графиков данных функций.

Из построения видно, что графики функций пересекаются в точках с координатами : (3;1) и(-1;-3).

Задание. Решить уравнение: 2 х^3 – x — 1=0

Перепишем его так : 2 х 3 = x + 1

Построим графики функций от левой и правой части уравнения:

у= 2 х 3 (графиком этой функции является кубическая парабола) и график от правой части уравнения :у=х+1

Из построения видно, что абсцисса точки пересечения является х=1. значит, в ответ нужно записать: х=1

Решим графическим способом такое уравнение : х 3 =8.

Строим графики функций: у = х 3 и у=8., затем найдем абсциссу точки пересечения графиков этих функций.

Задание. Решить уравнение: √x – 0.5x = 0

Перепишем так: √x = 0.5x

Построим графики функций: у= 0.5x и у = √x

Как видно из построения, графики функций пересекаются в двух точках:

Нас интересует только координата x.

Значит уравнение √x – 0.5x = 0 имеет два корня: x ₁ = 0 и x ₂ = 4.

7. Решение квадратных неравенств графическим способом.

Способ , который нам хорошо известен при изучении данной темы по учебнику.

Я же предлагаю переписать неравенство следующим образом : х^2-4>3х.

Построим графики функций от левой и правой частей неравенства.

Выделим ту часть, где график от левой части выше графика от правой части.

На мой взгляд такое решение более красивое , интересное и более понятное.

8. Решение линейных неравенств и систем неравенств графическим способом.

Называют ся линейными неравенствами .

График линейного или квадратного неравенства строится так же, как строится график любой функции (уравнения).

Разница заключается в том, что неравенство подразумевает наличие множества решений, поэтому график неравенства представляет собой не просто точку на числовой прямой или линию на координатной плоскости.

С помощью математических операций и знака неравенства можно определить множество решений неравенства

Вообще графический способ решения неравенств с одной переменной применяется не только для решения квадратных неравенств, но и неравенств других видов.

Суть графического способа решения неравенств следующая:

рассматривают функции y = f(x) и y = g(x) , которые соответствуют левой и правой частям неравенства, строят их графики в одной прямоугольной системе координат и выясняют, на каких промежутках график одной из них располагается ниже или выше другого.

Те промежутки, на которых график функции у = f (х) выше графика функции y = g(х) являются решениями неравенства f(x)>g(x) ;

график функции y = f(х) не ниже графика функции y = g(x) являются решениями неравенства f(x) ≥ g(x) ;

график функции у = f (х) ниже графика функции y = g(х) являются решениями неравенства f(x) ;

график функции y = f(х) не выше графика функции y = g(х) являются решениями неравенства f(x) ≤ g(x) .

Также скажем, что абсциссы точек пересечения графиков функций y = f(x) и y = g(x) , являются решениями уравнения f(x) = g(x) .

Мы рассмотрели графический метод решения уравнений и квадратных неравенств; рассмотрели конкретные примеры, при решении которых использовали некоторые свойства функций.

Иногда при графическом решении некоторых уравнений и неравенств корни определяются только приближённо в силу того, что невозможно с высокой точностью построить график функции, измерить абсциссы или ординаты точек пересечения графика с осями координат или с другими графиками. Тем не менее, той точности, которую обеспечивает графический метод, бывает вполне достаточно для практических нужд.

Построение графиков основывается на знании основных элементарных функций, и на основные методы построения графиков функций. В работе представлено достаточное количество примеров, раскрывающих графический метод решения линейных и квадратных уравнений и неравенств, который доступен для понимания .

Работа может быть использована для углубления и расширения знаний в области построения графиков функций и использовании графического метода при решении некоторых видов уравнений и неравенств. Теорию можно использовать так же при подготовки к экзаменам , к олимпиадам.

Я свою работу представляла учащимся 8-х и 9-х классов нашей школы. И продолжаю дополнять свои исследования , а именно находить красивые решения линейных неравенств и систем неравенств.

Это и закрепление изученных свойств функций, и прекрасная демонстрация их применения на практике.

В старших классах я буду ещё знакомиться с другими функциями , с другими уравнениями и неравенствами и м не интересно будет продолжить свой проект.

Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Графическое решение уравнений, неравенств

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

В ходе урока вы сможете самостоятельно изучить тему «Графическое решение уравнений, неравенств». Преподаватель на занятии разберет графические методы решения уравнений и неравенств. Научит строить графики, анализировать их и получать решения уравнений и неравенств. На уроке также будут разобраны конкретные примеры по этой теме.