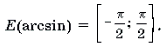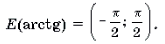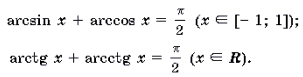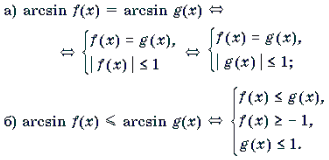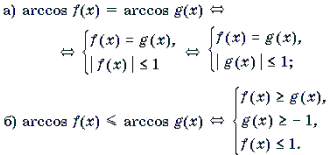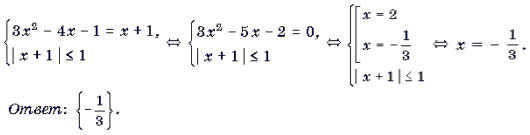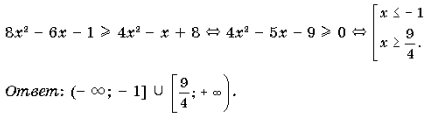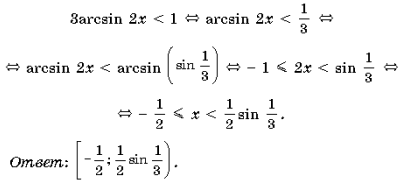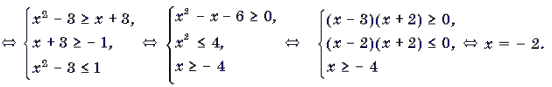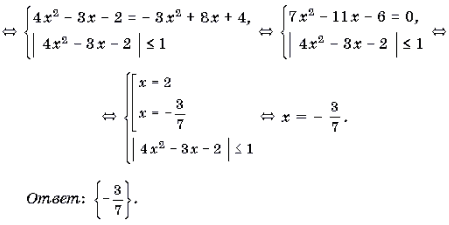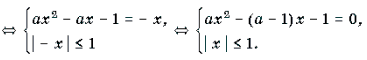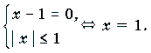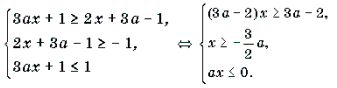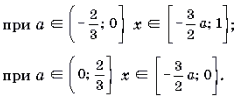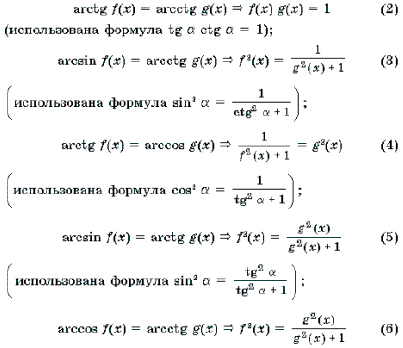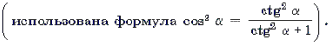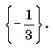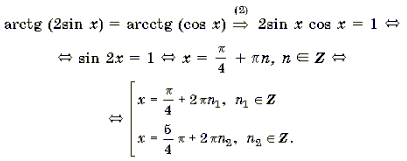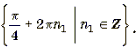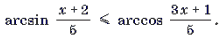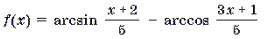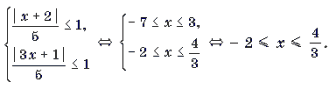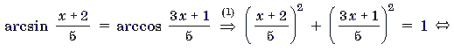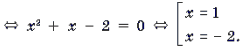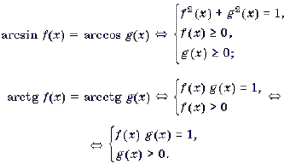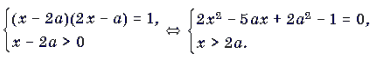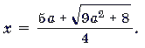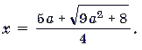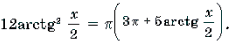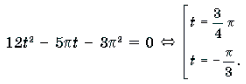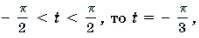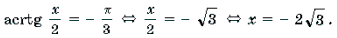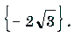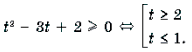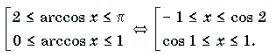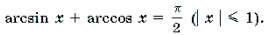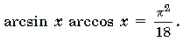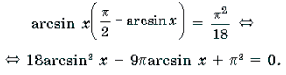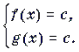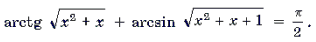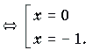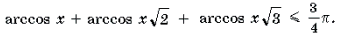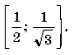Про уравнения - легко » Статьи

Решение уравнений и неравенств с арксинусами и арккосинусами

Обновлено
Уравнения и неравенства, содержащие обратные тригонометрические функции

Задачи, связанные с обратными тригонометрическими функциями, часто вызывают у школьников старших классов значительные трудности. Связано это, прежде всего, с тем, что в действующих учебниках и учебных пособиях подобным задачам уделяется не слишком большое внимание, и если с задачами на вычисление значений обратных тригонометрических функций учащиеся еще как-то справляются, то уравнения и неравенства, содержащие эти функции, нередко ставят их в тупик. Последнее не удивительно, поскольку практически ни в одном учебнике (включая учебники для классов с углубленным изучением математики) не излагается методика решения даже простейших уравнений и неравенств такого рода. Предлагаемая вашему вниманию статья посвящена методам решения уравнений и неравенств, содержащих обратные тригонометрические функции. Надеемся, что она окажется полезной для учителей, работающих в старших классах – как общеобразовательных, так и математических.

Вначале напомним важнейшие свойства обратных тригонометрических функций.

1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];

arcsin (– x) = – arcsin x (x О [– 1; 1]);
Решение уравнений и неравенств с арксинусами и арккосинусами

2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];

3 Функция y = arctg x определена и монотонно возрастает на R;

arctg (– x) = – arctg x (x О R);
Решение уравнений и неравенств с арксинусами и арккосинусами

4 Функция y = arcctg x определена и монотонно убывает на R;

5

Решение уравнений и неравенств с арксинусами и арккосинусами

Свойства монотонности и ограниченности являются ключевыми при решении многих уравнений и неравенств, содержащих обратные тригонометрические функции. Перейдем к рассмотрению методов решения этих уравнений и неравенств.

I. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями

Решение уравнений и неравенств, левая и правая части которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функций, как монотонность. Напомним, что функции y = arcsin t и y = arctg t монотонно возрастают, а функции y = arccos t и y = arcctg t монотонно убывают на своих областях определения. Поэтому справедливы следующие равносильные переходы.

1 .

Решение уравнений и неравенств с арксинусами и арккосинусами

2 .

Решение уравнений и неравенств с арксинусами и арккосинусами

3 .

4 .

Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | Ј 1 (тогда используем первую систему), или | g(x) | Ј 1 (в этом случае используем вторую систему).

Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).

Решение. Уравнение равносильно системе

Решение уравнений и неравенств с арксинусами и арккосинусами

Замечание 2. Решать неравенство, входящее в систему, вообще говоря, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении примера 1.

Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) Ј arcctg (4x 2 – x + 8).

Решение. Неравенство равносильно следующему:

Решение уравнений и неравенств с арксинусами и арккосинусами

Пример 3. Решить неравенство 3arcsin 2x

Решение уравнений и неравенств с арксинусами и арккосинусами

Пример 4. Решить неравенство arccos (x 2 – 3) Ј arccos (x + 3).

Решение уравнений и неравенств с арксинусами и арккосинусами

Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = p .

Решение. Так как p – arccos t = arccos (– t), то имеет место следующая цепочка равносильных преобразований:

arccos (4x 2 – 3x – 2) = p – arccos (3x 2 – 8x – 4) Ы
Ы arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4) Ы

Решение уравнений и неравенств с арксинусами и арккосинусами

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 7. Решить уравнение с параметром a: arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

Решение уравнений и неравенств с арксинусами и арккосинусами

Рассмотрим два случая:

1) a = 0. В этом случае система примет вид: Решение уравнений и неравенств с арксинусами и арккосинусами

2) a № 0. В этом случае уравнение системы является квадратным. Его корни: 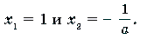Решение уравнений и неравенств с арксинусами и арккосинусами
Так как | x | Ј 1, то 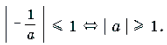Решение уравнений и неравенств с арксинусами и арккосинусами . Если a = – 1, то x2 = x1 = 1. Если a О (– Ґ Ч ; – 1) И [1; Ґ ), то уравнение имеет два корня.

Ответ: при 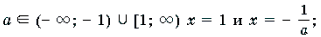Решение уравнений и неравенств с арксинусами и арккосинусами при a = – 1 и a = 0 x = 1; при прочих a решений нет.

Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) Ј arccos (2x + 3a – 1).

Решение. Неравенство равносильно системе Решение уравнений и неравенств с арксинусами и арккосинусами

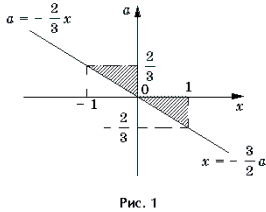
Решать последнюю систему можно графо-аналитическим методом, учитывая то, что при a > Решение уравнений и неравенств с арксинусами и арккосинусами первое неравенство системы равносильно неравенству x і 1, при a Решение уравнений и неравенств с арксинусами и арккосинусами – неравенству x Ј 1, при a = Решение уравнений и неравенств с арксинусами и арккосинусами решением первого неравенства является любое действительное число. Множество всех точек (x; a) плоскости Oxa, удовлетворяющих системе, показано на рис. 1 штриховкой.

Решение уравнений и неравенств с арксинусами и арккосинусамиОтвет: при | a | > Решение уравнений и неравенств с арксинусами и арккосинусамирешений нет; при a = – Решение уравнений и неравенств с арксинусами и арккосинусамиx = 1;

Решение уравнений и неравенств с арксинусами и арккосинусами

II. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями

При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Эта группа задач является чуть более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x0 – решение этого уравнения. Обозначим arcsin f(x0) = arccos g(x0) через a. Тогда sin a = f(x0), cos a = g(x0), откуда f 2 (x0) + g 2 (x0) = 1. Итак, arcsin f(x) = arccos g(x) Ю f 2 (x) + g 2 (x) = 1. (1)

Рассуждая аналогично, можно получить следующие переходы:

Решение уравнений и неравенств с арксинусами и арккосинусами

Решение уравнений и неравенств с арксинусами и арккосинусами

Замечание 3. Корнем каждого из уравнений (1)–(4) может быть только такое число x0, для которого f(x0) і 0 и g(x0) і 0. В противном случае множество значений левой и правой частей уравнения не пересекаются.

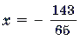
Пример 9. Решить уравнение Решение уравнений и неравенств с арксинусами и арккосинусами

Решение уравнений и неравенств с арксинусами и арккосинусами

Корень Решение уравнений и неравенств с арксинусами и арккосинусами является посторонним.

Пример 10. Решить уравнение Решение уравнений и неравенств с арксинусами и арккосинусами

Решение уравнений и неравенств с арксинусами и арккосинусами

Корень x = – 2 является посторонним.

Ответ: . Решение уравнений и неравенств с арксинусами и арккосинусами

Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).

Решение уравнений и неравенств с арксинусами и арккосинусами

Корни вида 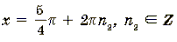Решение уравнений и неравенств с арксинусами и арккосинусами являются посторонними.

Ответ: Решение уравнений и неравенств с арксинусами и арккосинусами

При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в некоторых случаях учитывать свойства монотонных функций.

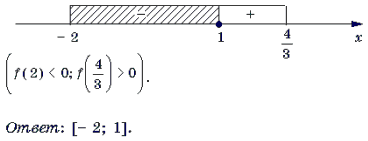
Пример 12. Решить неравенство Решение уравнений и неравенств с арксинусами и арккосинусами

Решение. Рассмотрим функцию Решение уравнений и неравенств с арксинусами и арккосинусами

и решим неравенство f(x) Ј 0 методом интервалов.

1) Найдем D(f). Для этого решим систему

Решение уравнений и неравенств с арксинусами и арккосинусами

2) Найдем нули f(x). Для этого решим уравнение

Решение уравнений и неравенств с арксинусами и арккосинусами

Решение уравнений и неравенств с арксинусами и арккосинусами

Корень x = – 2 является посторонним.

3) Решим неравенство f(x) Ј 0 методом интервалов.

Решение уравнений и неравенств с арксинусами и арккосинусами

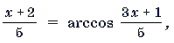
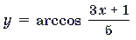
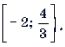
Замечание 4. Заметим, что найдя корень уравнения Решение уравнений и неравенств с арксинусами и арккосинусами можно было не обращаться к методу интервалов, а воспользоваться тем, что функция Решение уравнений и неравенств с арксинусами и арккосинусами является монотонно возрастающей, а функция Решение уравнений и неравенств с арксинусами и арккосинусами монотонно убывающей на отрезке Решение уравнений и неравенств с арксинусами и арккосинусами . Поэтому решением исходного неравенства является промежуток [– 2; 1]. Следует, однако, понимать, что метод интервалов является более универсальным, – ведь его можно применять и в тех случаях, когда использование свойств монотонных функций не приводит к искомому результату.

При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например,

Решение уравнений и неравенств с арксинусами и арккосинусами

Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).

Решение. Данное уравнение равносильно системе Решение уравнений и неравенств с арксинусами и арккосинусами

Графиком квадратного трехчлена f(x) = 2x 2 – 5ax + 2a2 – 1 является парабола, ветви которой направлены вверх. Поскольку f(2a) = – 1 2a. Это корень Решение уравнений и неравенств с арксинусами и арккосинусами

Ответ: при любом a Решение уравнений и неравенств с арксинусами и арккосинусами

III. Замена переменной

Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно свести к алгебраическим, сделав соответствующую замену переменной. При этом следует помнить о естественных ограничениях на вводимую переменную, связанных с ограниченностью обратных тригонометрических функций.

Пример 14. Решить уравнение Решение уравнений и неравенств с арксинусами и арккосинусами

Решение. Обозначим 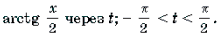Решение уравнений и неравенств с арксинусами и арккосинусами После преобразований получим уравнение

Решение уравнений и неравенств с арксинусами и арккосинусами

Поскольку Решение уравнений и неравенств с арксинусами и арккосинусами

откуда Решение уравнений и неравенств с арксинусами и арккосинусами

Ответ: Решение уравнений и неравенств с арксинусами и арккосинусами

Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 і 2.

Решение. Пусть arccos x = t, 0 Ј t Ј p . Тогда Решение уравнений и неравенств с арксинусами и арккосинусами

Поскольку 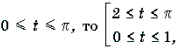Решение уравнений и неравенств с арксинусами и арккосинусами откуда Решение уравнений и неравенств с арксинусами и арккосинусами

Ответ: [– 1; cos 2] И [cos 1; 1].

Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества

Решение уравнений и неравенств с арксинусами и арккосинусами

Пример 16. Решить уравнение Решение уравнений и неравенств с арксинусами и арккосинусами

Решение. Данное уравнение равносильно следующему:

Решение уравнений и неравенств с арксинусами и арккосинусами

Пусть arcsin x = t, Решение уравнений и неравенств с арксинусами и арккосинусами

Тогда Решение уравнений и неравенств с арксинусами и арккосинусами

Решение уравнений и неравенств с арксинусами и арккосинусами

Решение уравнений и неравенств с арксинусами и арккосинусами

IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций

Решение некоторых уравнений и неравенств, содержащих обратные тригонометрические функции, основывается исключительно на таких свойствах этих функций, как монотонность и ограниченность. При этом используются следующие теоремы.

Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.

Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.

Теорема 3. Если 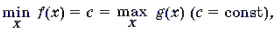Решение уравнений и неравенств с арксинусами и арккосинусами то на множестве X уравнение f(x) = g(x) равносильно
системе Решение уравнений и неравенств с арксинусами и арккосинусами

Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.

Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.

Пример 18. Решить уравнение Решение уравнений и неравенств с арксинусами и арккосинусами

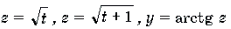
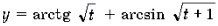
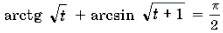
Решение. Пусть x 2 + x = t. Тогда уравнение примет вид Решение уравнений и неравенств с арксинусами и арккосинусами

Функции Решение уравнений и неравенств с арксинусами и арккосинусамиявляются монотонно возрастающими. Поэтому функция Решение уравнений и неравенств с арксинусами и арккосинусамитакже является монотонно возрастающей. В силу теоремы 1 уравнение Решение уравнений и неравенств с арксинусами и арккосинусамиимеет не более одного корня. Очевидно, что t = 0 является корнем этого уравнения. Поэтому x 2 + x = 0 Решение уравнений и неравенств с арксинусами и арккосинусами

Пример 19. Решить неравенство Решение уравнений и неравенств с арксинусами и арккосинусами

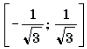
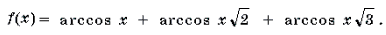
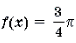
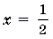
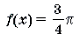
Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке Решение уравнений и неравенств с арксинусами и арккосинусамифункцию Решение уравнений и неравенств с арксинусами и арккосинусамиУравнение Решение уравнений и неравенств с арксинусами и арккосинусамив силу теоремы 1 имеет не более одного корня. Очевидно, что Решение уравнений и неравенств с арксинусами и арккосинусами– корень этого уравнения. Поэтому решением неравенства Решение уравнений и неравенств с арксинусами и арккосинусамиявляется отрезок Решение уравнений и неравенств с арксинусами и арккосинусами

Ответ: Решение уравнений и неравенств с арксинусами и арккосинусами

Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = p .

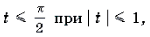
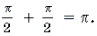
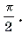
Решение. Поскольку arcsin Решение уравнений и неравенств с арксинусами и арккосинусамито левая часть уравнения не превосходит Решение уравнений и неравенств с арксинусами и арккосинусамиЗнак равенства возможен, лишь если каждое слагаемое левой части равно Решение уравнений и неравенств с арксинусами и арккосинусами. Таким образом, уравнение равносильно системе:

Решение уравнений и неравенств с арксинусами и арккосинусами

Решение последней системы не представляет труда.

Содержание
  1. Презентация по математике на тему «Решение тригонометрических уравнений и неравенств. Арксинус, арккосинус, арктангенс»
  2. Описание презентации по отдельным слайдам:
  3. Краткое описание документа:
  4. Математика: теория и методика преподавания в образовательной организации
  5. Дистанционное обучение как современный формат преподавания
  6. Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
  7. Дистанционные курсы для педагогов
  8. Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
  9. Другие материалы
  10. Вам будут интересны эти курсы:
  11. Оставьте свой комментарий
  12. Автор материала
  13. Дистанционные курсы для педагогов
  14. Подарочные сертификаты
  15. Арксинус. Решение простейших уравнений с синусом. Часть 2
  16. Арксинусом числа (a) ((a∈[-1;1])) называют число (x∈[-frac;frac]) синус которого равен (a) т.е.
  17. Как вычислить арксинус?
  18. Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от (-frac) до (frac) ) равен аргументу арксинуса?
  19. Зачем нужен арксинус? Решение уравнения (sin x=a)
  20. Если (sin ⁡x) равен не табличному значению между (1) и (-1), то решения будут выглядеть как: ( left[ beginx= arcsin a +2πn, n∈Z\ x=π- arcsin a +2πl, l∈Zendright.)
  21. Арксинус отрицательного числа
  22. 🎦 Видео

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функции

Презентация по математике на тему «Решение тригонометрических уравнений и неравенств. Арксинус, арккосинус, арктангенс»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Решение уравнений и неравенств с арксинусами и арккосинусами

Описание презентации по отдельным слайдам:

Решение уравнений и неравенств с арксинусами и арккосинусами

Решение тригонометрических уравнений и неравенств Арксинус, арккосинус и арктангенс

Решение уравнений и неравенств с арксинусами и арккосинусами

Теорема о корне

Решение уравнений и неравенств с арксинусами и арккосинусами

Решение уравнений и неравенств с арксинусами и арккосинусами

Решение уравнений и неравенств с арксинусами и арккосинусами

Решение уравнений и неравенств с арксинусами и арккосинусами

Краткое описание документа:

Решение тригонометрических уравнений и неравенств Арксинус, арккосинус и арктангенс Теорема о корне Арксинус Арккосинус Арктангенс Арккотангенс

Решение уравнений и неравенств с арксинусами и арккосинусами

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

  • Сейчас обучается 694 человека из 75 регионов

Решение уравнений и неравенств с арксинусами и арккосинусами

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

  • Сейчас обучается 867 человек из 78 регионов

Решение уравнений и неравенств с арксинусами и арккосинусами

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

  • Сейчас обучается 52 человека из 24 регионов

«Профессиональный имидж педагога: стереотипы и методы их преодоления»

Свидетельство и скидка на обучение каждому участнику

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

  • Для всех учеников 1-11 классов
    и дошкольников
  • Интересные задания
    по 16 предметам

Решение уравнений и неравенств с арксинусами и арккосинусами Решение уравнений и неравенств с арксинусами и арккосинусами

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnline

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 840 276 материалов в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

  • 01.10.2015
  • 468
  • 0
  • 01.10.2015
  • 4457
  • 25
  • 01.10.2015
  • 842
  • 0
  • 01.10.2015
  • 1494
  • 0
  • 01.10.2015
  • 1123
  • 1
  • 01.10.2015
  • 22143
  • 30

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

  • 01.10.2015 1327
  • PPTX 465.8 кбайт
  • 3 скачивания
  • Оцените материал:

Настоящий материал опубликован пользователем Уильямс Майк (Отсутствует). Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Решение уравнений и неравенств с арксинусами и арккосинусами

  • На сайте: 6 лет и 10 месяцев
  • Подписчики: 102
  • Всего просмотров: 320479
  • Всего материалов: 160

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

10 класс, 22 урок, Простейшие тригонометрические уравнения неравенства

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Решение уравнений и неравенств с арксинусами и арккосинусами

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Решение уравнений и неравенств с арксинусами и арккосинусами

Вузы РФ не будут повышать стоимость обучения на первом курсе

Время чтения: 1 минута

Решение уравнений и неравенств с арксинусами и арккосинусами

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Решение уравнений и неравенств с арксинусами и арккосинусами

Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства

Время чтения: 1 минута

Решение уравнений и неравенств с арксинусами и арккосинусами

Минобрнауки отменило плановые и внеплановые проверки вузов в 2022 году

Время чтения: 1 минута

Решение уравнений и неравенств с арксинусами и арккосинусами

Эвакуированные в Россию из ДНР и ЛНР дети смогут поступить в вузы по квоте

Время чтения: 1 минута

Решение уравнений и неравенств с арксинусами и арккосинусами

Инфофорум о буллинге в школе: итоги и ключевые идеи

Время чтения: 6 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.

Арксинус. Решение простейших уравнений с синусом. Часть 2

Арксинусом числа (a) ((a∈[-1;1])) называют число (x∈[-frac;frac]) синус которого равен (a) т.е.

Проще говоря, арксинус обратен синусу.

На круге это выглядит так:

Решение уравнений и неравенств с арксинусами и арккосинусами Решение уравнений и неравенств с арксинусами и арккосинусами

Видео:ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА 10 класс тригонометрияСкачать

ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА 10 класс тригонометрия

Как вычислить арксинус?

Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от (-frac) до (frac) ) равен аргументу арксинуса?

Например, вычислите значение арксинуса:

а) Синус какого числа равен (-frac)? Или в более точной формулировке можно спросить так: если (sin ⁡x=-frac), то чему равен (x)? Причем, обратите внимание, нам нужно такое значение, которое лежит между (-frac) и (frac). Ответ очевиден:

б) Синус какого числа равен (frac<sqrt>)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ (frac).

в) Синус от чего равен (-1)?
Иначе говоря, (sin ⁡x=-1), (x=) ?

Тригонометрический круг со всеми стандартными арксинусами:

Решение уравнений и неравенств с арксинусами и арккосинусами

Видео:Как решать тригонометрические неравенства?Скачать

Как решать тригонометрические неравенства?

Зачем нужен арксинус? Решение уравнения (sin x=a)

Чтобы понять зачем придумали арксинус, давайте решим уравнение: (sin ⁡x=frac).

Это не вызывает затруднений:

Решение уравнений и неравенств с арксинусами и арккосинусами

Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.

А теперь решите уравнение: (sin ⁡x=frac).

Решение уравнений и неравенств с арксинусами и арккосинусами

Что тут будет ответом? Не (frac), не (frac), даже не (frac) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?

Вот тут-то на помощь и приходит арксинус! Значение правой точки равно (arcsin⁡frac), потому что известно, что синус равен (frac). Длина дуги от (0) до правой точки тогда тоже будет равна (arcsin⁡frac). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному (arcsin⁡frac) от (π), то её значение составляет (π- arcsin⁡frac).

Ок, значение этих двух точек нашли. Теперь запишем полный ответ: ( left[ beginx=arcsin frac+2πn, n∈Z\ x=π-arcsin frac+2πl, l∈Zendright.) Без арксинусов решить уравнение (sin ⁡x=frac) не получилось бы. Как и уравнение (sin ⁡x=0,125), (sin ⁡x=-frac), (sin⁡ x=frac<sqrt>) и многие другие. Фактически без арксинуса мы можем решать только (9) простейших уравнений с синусом:

Решение уравнений и неравенств с арксинусами и арккосинусами

С арксинусом – бесконечное количество.

Пример. Решите тригонометрическое уравнение: (sin ⁡x=frac<sqrt>).
Решение:

Решение уравнений и неравенств с арксинусами и арккосинусами

Пример. Решите тригонометрическое уравнение: (sin ⁡x=frac<sqrt>).

Решение:
Кто поторопился написать ответ ( left[ beginx=arcsin frac<sqrt>+2πn, n∈Z\ x=π-arcsin frac<sqrt>+2πl, l∈Zendright.), тот на ЕГЭ потеряет 2 балла. Дело в том, что в отличии от прошлых примеров (arcsin⁡ frac<sqrt>) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента. Для этого умножим и числитель и знаменатель дробь на корень из двух (frac<sqrt> = frac<1 cdot sqrt> <sqrtcdot sqrt>= frac<sqrt>). Таким образом, получаем:

Значит в ответе вместо арксинусов нужно написать (frac).

Пример. Решите тригонометрическое уравнение: (sin ⁡x=frac).

Решение:
И вновь тот, кто поторопился написать ( left[ beginx= arcsin frac+2πn, n∈Z\ x=π- arcsinfrac+2πl, l∈Zendright.) на ЕГЭ потеряет (2) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать (arcsin⁡frac)? Пролистайте до самого верха, туда, где было определение арксинуса. Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен (1) и больше или равен (-1). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.

Решение уравнений и неравенств с арксинусами и арккосинусами

Думаю, вы уловили закономерность.

Если (sin ⁡x) равен не табличному значению между (1) и (-1), то решения будут выглядеть как: ( left[ beginx= arcsin a +2πn, n∈Z\ x=π- arcsin a +2πl, l∈Zendright.)

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по Математике

Арксинус отрицательного числа

Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:

Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:

Решение уравнений и неравенств с арксинусами и арккосинусами

Удивил последний пример? Почему в нем формула не работает? Потому что запись (arcsin⁡(-frac<sqrt>)) в принципе неверна, ведь (-frac<sqrt> Синус
Тригонометрические уравнения

🎦 Видео

Преобразование выражений, содержащих арксинус, арккосинус, арктангенс и арккотангенс. 2 ч. 10 класс.Скачать

Преобразование выражений, содержащих арксинус, арккосинус, арктангенс и арккотангенс. 2 ч. 10 класс.

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor online

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэ

Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.

Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Математика| Преобразование тригонометрических выражений. Формулы и задачи

Решение тригонометрических неравенств. 10 класс.Скачать

Решение тригонометрических неравенств. 10 класс.

ТРИГОНОМЕТРИЯ ЗА 7 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

ТРИГОНОМЕТРИЯ ЗА 7 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по Математике

Вычисление аркфункцийСкачать

Вычисление аркфункций

Обратные тригонометрические функции, y=arcsinx и y=arccosx, их свойства и графики. 10 класс.Скачать

Обратные тригонометрические функции, y=arcsinx и y=arccosx, их свойства и графики. 10 класс.

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

10 класс, 23 урок, Методы решения тригонометрических уравнений

Решение тригонометрических неравенств. 10 класс.Скачать

Решение тригонометрических неравенств. 10 класс.

ЕГЭ №9. Тригонометрические выражения.Тригонометрические уравнения | Математика | TutorOnlineСкачать

ЕГЭ №9. Тригонометрические выражения.Тригонометрические уравнения | Математика | TutorOnline

Преобразование выражений, содержащих арккосинус, арксинус, арктангенс и арккотангенс. 1ч. 10 класс.Скачать

Преобразование выражений, содержащих арккосинус, арксинус, арктангенс и арккотангенс. 1ч. 10 класс.
Поделиться или сохранить к себе: