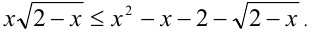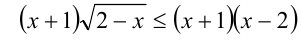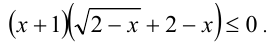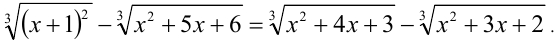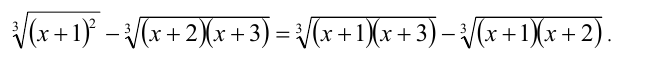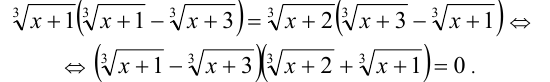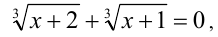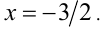- Решение уравнений разложения на множители (метод расщепления) – это способ решения уравнений при котором мы стремимся уравнение свести их к виду:
- В результате умножения ноль можно получить, только если один из множителей равен нулю.
- Алгебра и начала математического анализа. 10 класс
- Метод решения
- Метод разложения на множители уравнений и неравенств
- Разложение на множители
- Пример №348.
- Пример №349.
- 📸 Видео
Решение уравнений разложения на множители (метод расщепления) – это способ решения уравнений при котором мы стремимся уравнение свести их к виду:
а затем каждую скобку приравнять к нулю и решить как отдельное уравнение.
Вынесем за скобку икс.
Разобьем уравнение на два простейших.
В первом корень уравнения уже понятен, во втором надо перенести (5) в правую сторону.
Решение методом разложения на множители основывается на простой идее:
В результате умножения ноль можно получить, только если один из множителей равен нулю.
Попробуйте придумать два числа, которые при умножении дают ноль. Вы убедитесь, что хотя бы одно из них обязательно должно быть нулем.
Этот метод решения уравнений один из самых популярных, поэтому освоить его очень важно для тех, кто планирует иметь четверки и пятерки. А для освоения этого метода, конечно, надо уметь раскладывать на множители как Бог: знать все формулы сокращенного умножения, легко выносить множители за скобки, уметь применять метод группировки и т.д. Подробнее о всех способах разложения на множители смотри здесь .
Пример(задание из ОГЭ). Решите уравнение (x^3+4x^2-4x-16=0).
Решение:
Перед нами кубическое уравнение.
Применим метод группировки: из первой пары слагаемых вынесем (x^2), а из второй – минус четверку.
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №12. Решение алгебраических уравнений разложением на множители.
Перечень вопросов, рассматриваемых в теме
1) типы алгебраических уравнений;
2) решение алгебраические уравнения методом разложения на множители;
3) методы решения алгебраических уравнений.
Глоссарий по теме
Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x1, x2, …, xn)=0, где P — многочлен от переменных x1, x2, …, xn, которые называются неизвестными.
Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнение над множеством F.
Степенью алгебраического уравнения называют степень многочлена P.
Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
Биквадратными называются уравнения вида ах 4 + bх 2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.
Симметрическим уравнением 3-ей степени называют уравнение вида: ax 3 + bx 2 + bx + a = 0, где a, b – заданные числа.
Уравнение вида a n x n +a n-1 x n-1 +…+a 1 x+a 0 =0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a n-1 =a k , при k=0, 1, …, n.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Давайте вспомним, что такое алгебраическое уравнение?
Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x1, x2, …, xn)=0, где P — многочлен от переменных x1, x2, …, xn, которые называются неизвестными.
Коэффициенты многочлена P обычно берутся из некоторого поля F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнение над полем F.
Степенью алгебраического уравнения называют степень многочлена P.

Связанные определения. Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
Примеры и разбор решения заданий тренировочного модуля
- Алгебраические уравнения, решаемые разложением на множители:
D(–2) : 
Можно догадаться, что число х1 = –1 является корнем этого уравнения, так как –1 + 3 – 2 = 0.
х + 1 = 0 или х 2 –х–2 = 0;
х1 = –1 х2,3 = 
х2,3 = 
x 3 + х 2 – х 2 – х – 2x – 2 = 0;
(x 3 + х 2 ) – (х 2 + х) – 2(x + 1) = 0;
х 2 (х + 1) – х(х + 1) – 2(х + 1) = 0;
(х + 1) (х + 1) (х –2) = 0;

- Уравнения, сводящиеся к алгебраическим
- Биквадратные уравнения
На прошлом уроке мы познакомились с данным видом уравнений
Определение. Биквадратными называются уравнения вида ах 4 + bх 2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.
Метод решения
Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки у=х 2 .
Новое квадратное уравнение относительно переменной у: ay 2 +by+c=0.
Решая это уравнение, мы получаем корни квадратного уравнения
Решая эти два уравнения (y1=x1 2 и y2=x1 2 ) относительно переменной x, мы получаем корни данного биквадратного уравнения.
Порядок действий при решении биквадратных уравнений
- Ввести новую переменную у=х 2
- Подставить данную переменную в исходное уравнение
- Решить квадратное уравнение относительно новой переменной
- После нахождения корней (y1; y2) подставить их в нашу переменную у=х 2 и найти исходные корни биквадратного уравнения
х 4 – 8х 2 – 9 = 0.
Решение: Пусть у = х 2 , где у 
По формулам Виета:
Первое решение отбрасываем ( у 
а из второго находим х1 = –3; х2 = 3.
2 Симметрические уравнения
Решение симметрических уравнений рассмотрим на примере симметрических уравнений третьей степени.
Симметрическим уравнением 3-ей степени называют уравнение вида ax 3 + bx 2 + bx + a = 0, где a, b – заданные числа.
Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства симметрических уравнений:
1 0 . У любого симметрического уравнения нечетной степени всегда есть корень, равный -1.
Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х 3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е.
(х + 1)(ах 2 + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах 2 + (b – а)x + а = 0,
первое уравнение и доказывает интересующее нас утверждение.
2 0 . У симметрического уравнения корней, равных нулю, нет.
3 0 . При делении многочлена нечетной степени на (х + 1) частное является снова симметрическим многочленом.
х 3 + 2x 2 + 2х + 1 = 0.
Решение: У исходного уравнения обязательно есть корень х = –1.
Разлагая далее левую часть на множители, получим
(х + 1)(x 2 + х + 1) = 0.
x 2 + х + 1 = 0 не имеет корней.
2 Возвратные уравнения
Уравнение вида a n x n +a n-1 x n-1 +…+a 1 x+a 0 =0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a n-1 =a k , при k=0, 1, …, n.
Рассмотрим возвратное уравнение четвёртой степени вида
ax⁴ + bx³ + cx² + bx + a = 0, где a, b и c — некоторые числа, причём a ≠ 0. Оно является частным случаем уравнения ax⁴ + bx³ + cx² + kbx + k²a = 0 при k = 1.
Порядок действий при решении возвратных уравнений вида ax 4 + bx 3 + cx 2 + bx + a = 0:
- разделить левую и правую части уравнения на
. При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
- группировкой привести полученное уравнение к виду
- ввести новую переменную
, тогда выполнено
, то есть
;
в новых переменных рассматриваемое уравнение является квадратным: at 2 +bt+c–2a=0;
- решить его относительно t, возвратиться к исходной переменной.
Решение: Разделим на x 2 , получим:
Введем замену:
Пусть
Видео:Алгебра 10 класс (Урок№12 - Решение алгебраических уравнений разложением на множители.)Скачать

Метод разложения на множители уравнений и неравенств
Разложение на множители
Это общий метод, который может быть использован при решении любых, не обязательно алгебраических, уравнений и неравенств. Под разложением на множители некоторого многочлена, вообще говоря, произвольного вида (алгебраического, тригонометрического и т.д.) понимают его представление в виде произведения нескольких сомножителей. В результате разложения на множители решаемое уравнение оказывается сведено к решению на ОДЗ совокупности нескольких, как правило, более простых уравнений. Для разложения на множители существуют различные приёмы, включая группировку и вынесение общего множителя за скобку, одновременное прибавление и вычитание некоторого одночлена или же, наоборот, разбиение одночлена на сумму (разность) нескольких, и другие.
При решении неравенств разложение на множители часто используют для приведения неравенства к виду, удобному для последующего применения метода интервалов.
Пример №348.
Решение:
Преобразуем неравенство к виду
откуда получаем следующее разложение на множители
Так как на ОДЗ 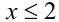
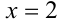
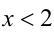
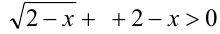
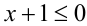
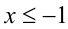
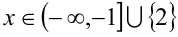
Пример №349.
Решение:
Найдя корни, разложим квадратные трёхчлены под радикалами на линейные множители:
Далее, группируя и вынося общие множители за скобки, получим
Заметим, что выражение в первых скобках в нуль не обращается. Таким образом, исходное уравнение равносильно уравнению
решая которое находим единственный корень
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📸 Видео
РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ / Алгебра 7 классСкачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Решение уравнений с помощью разложения на множители | Алгебра 7 класс #23 | ИнфоурокСкачать

Разложение кубических выражений на множителиСкачать

Математика| Разложение квадратного трехчлена на множители.Скачать

РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ | Решение неравенств разложением на множители и методом интервалов.Скачать

Схема Горнера. 10 класс.Скачать

Разложение на множители. 7 класс. Вебинар | МатематикаСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Теорема Безу и разложение многочлена на множителиСкачать

Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать

решение УРАВНЕНИЙ решение НЕРАВЕНСТВ 10 11 классСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

ОГЭ. Задание 21. Уравнение третей степени. Разложение на множители.Скачать

11 класс, 3 урок, Уравнения высших степенейСкачать

Решение уравнений методом разложения на множителиСкачать

Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Математика | Кубические уравнения по методу СталлонеСкачать



 . При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
. При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
 , тогда выполнено
, тогда выполнено  , то есть
, то есть  ;
;