Решение уравнений и круги эйлера

Решение логических задач с помощью кругов Эйлера

Круги Эйлера – задачи на пересечение или объединение множеств Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.

Задача 1. В классе 35 учеников. Из них 20 человек занимаются в математическом кружке, 11 — в биологическом, 10 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?

Изобразим эти кружки на рисунке. Мо­жем, например, начертить в школьном дворе большой круг, а в нем два поменьше. В левый круг, обозначенный буквой М, поместим всех математиков, а в правый, обозначенный буквой Б, всех биологов. Очевидно, в общей части кругов, обозна­ченной буквами МБ, окажутся те самые биологи-математики, ко­торые нас интересуют. Остальных ребят класса, а их 10, попросим не выходить из внешнего круга, самого большого. Теперь посчита­ем: всего внутри большого круга 35 ребят, внутри двух меньших 35 — 10 = 25 ребят. Внутри «математического» круга М находятся 20 ребят, значит, в той части «биологического» круга, которая рас­положена вне круга М, находятся 25 — 20 = 5 биологов, не посе­щающих математический кружок. Остальные биологи, их 11 — 5= = 6 человек, находятся в общей части кругов МБ. Таким образом, 6 биологов увлекаются математикой.

Задача 2. .В классе 38 человек. Из них 16 играют в баскетбол, 17 — в хоккей, 18 — в футбол. Увлекаются двумя видами спорта — баскетболом и хоккеем — четверо, баскетболом и футболом — трое, футболом и хоккеем — пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом.

Сколько ребят увлекаются одновременно тремя видами спорта?

Сколько ребят увлекается лишь одним из этих видов спорта?

Решение. Воспользуемся кругами Эйлера. Пусть большой круг изображает всех учащихся класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов. Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта. Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта — баскетболом занимаются 16 — (4 + z + 3) = 9 — z; одним лишь хоккеи 17 — (4 + z + 5) = 8 — z;

одним лишь футболом 18 — (3 + z + 5) = 10 — z.

Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам:

3 + (9 — z) + (8 — z) + (10 — z) + 4 + 3 + 5 + z = 38,

Таким образом, двое ребят увлекаются всеми тремя видами спорта.

Складывая числа 9 — z, 8 — z и 10 — z, где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек.

Двое ребят увлекаются всеми тремя видами спорта человека.

Увлекающихся лишь одним видом спорта: 21 человек.

Задача 3. Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».

11 – 6 = 5 – человек, которые смотрели только «Стиляги».

Ответ. 5 человек смотрели только «Стиляги».

Задача 4. Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?

В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

Получаем:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».

Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.

Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».

Задача 5. В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?

Изобразим эти множества на кругах Эйлера.

Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры:

Ответ: 6 покупателей купили диски и Максим, и Земфиры.

Задача 6. На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. прочитал 11 книг. Сколько книг прочитал Рон?

Учитывая условия задачи, чертеж будет таков:

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,

26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон.

Ответ. 8 книг прочитал Рон.

Задача 7. В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?

Изобразим множества следующим образом:

70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке. Только спортом заняты 5 человек.

Ответ. 5 человек заняты только спортом.

Задача 8. Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.

Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.

Видео:Круги Эйлера. Логическая задача на множества. Иностранные языкиСкачать

Решение задач с помощью кругов Эйлера

Классы: 5 , 6 , 7

Ключевые слова: круги Эйлера

Пояснительная записка

Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.

В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.

Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.

Основные понятия

Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.

Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

2. Решение задач с помощью кругов Эйлера

2.1. «Обитаемый остров» и «Стиляги»

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение:

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,

2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».

Ответ: 5 человек.

2.2. Задача про библиотеки

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.

1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?

Решение:

Чертим два множества таким образом:

1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,

3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,

4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,

5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.

Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.

Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.

2.3. Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

Решение:

Учитывая условия задачи, сделаем чертеж:

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.

Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.

Ответ: 8 книг.

2.4. Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Чертим три круга, таким образом:

Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».

1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,

2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,

3) 38 — (11 + 3 + 1 + 2 + 6 + 7) = 8 — ребят выбрали «Губка Боб Квадратные Штаны».

4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».

Ответ: 17 учеников.

2.5. Задача про Крейсер и Линкор

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Найдено страниц, тыс.

Крейсер и Линкор

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.)

Решение:

При помощи кругов Эйлера изобразим условия задачи.

1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,

2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,

3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.

Ответ: 2300 тыс. страниц.

2.6. Задача про блондинок

Каждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?

Решение:

Изобразим с помощью кругов Эйлера данные из задачи:

1) 12 — 1 = 11 (учеников) — девочек блондинок,

2) 12 — 1 = 11 (учеников) — блондины и любят математику,

3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,

4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,

5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,

6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,

7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) — всего в классе.

Ответ: 32 ученика.

2.7. Задача про кружки

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение:

Учитывая условия задачи, сделаем чертеж:

1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,

2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,

3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,

4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,

5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,

6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,

7) 70 — (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

Ответ: 10 человек и 11 человек.

Задачи для самостоятельного решения

1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?

2. Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

3. 12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?

5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?

6. В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?

7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?

8. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?

9. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Список использованных источников

1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.

2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.

Видео:Простое объяснения решения задач при помощи кругов ЭйлераСкачать

Круги Эйлера — примеры и методы решения логических задач

Видео:Множества и круги Эйлера для 8 задания на ОГЭ по информатике 2024 | УмскулСкачать

Множества в математике

Диаграммы Венна помогают показать связь теории множеств и логических операций. Круги Эйлера, множества чисел и других предметов тесно связаны. Под множеством понимается совокупность каких-то объектов, называемых элементами. В множества можно объединять объекты с общим признаком. Например, множество студентов второго курса университета или множество статей, написанных одним учёным. Можно выделить три вида таких математических объектов:

• конечное, например, множество стран;
• бесконечное — множество звёзд во вселенной;
• пустое — множество острых углов в прямоугольнике.

Группа элементов, составляющая множество, входящее в другое, более обширное множество называется подмножеством. Такое отношение получается между множеством действительных чисел и входящим в его состав подмножеством натуральных чисел.

В курсах информатики и обычно изучаются такие темы как «Введение в математическую логику» и «Поиск информации в Интернет». При решении задач по этим темам помощь оказывают диаграммы Венна. Для их построения можно использовать онлайн-калькулятор. Обозначения операций над множествами, которым должны соответствовать обозначения в калькуляторе:

• дополнение ¯A в калькуляторе имеет вид A’;
• пересечение A∩B представлено как A intersection B;
• объединение А⋃B обозначено A union B;
• симметрическая разность A∆B — symmetric difference of A and B;
• Относительное дополнение AB — AB.

Калькулятор выдаёт результат и подробное решение с правильным порядком операций при подстановке конкретных множеств.

Кольцом в теории множеств называют непустую систему R, замкнутую относительно пересечения и симметрической разности, то есть при пересечении или операции симметрической разности любых двух множеств обязательно получается множество, входящее в R. Это означает, что для любых элементов A, B из кольца элементы A∩B и A∆B будут лежать в кольце.

Видео:Круги Эйлера. Решение задач на поиск информации в Интернет. ИнформатикаСкачать

Отношения между понятиями

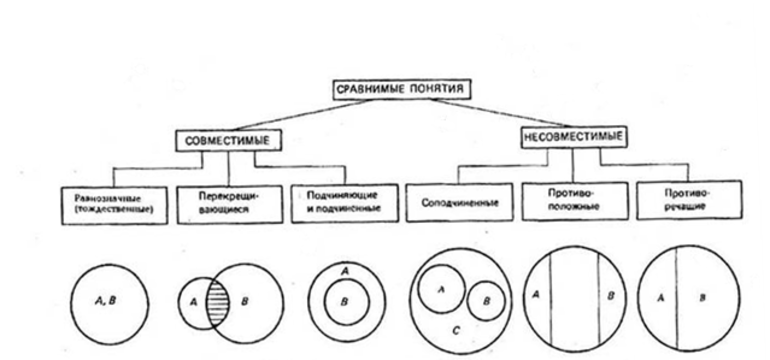
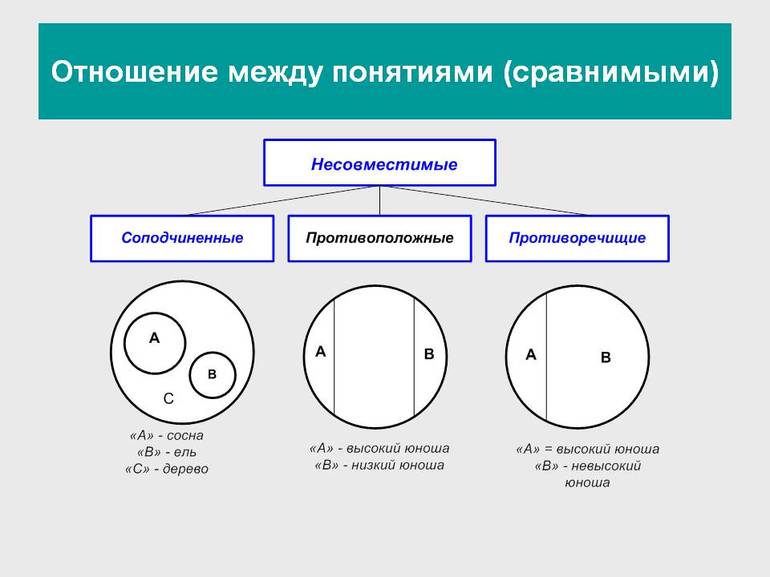
Логические операции, разрешающие доказывать утверждения и делать выводы, основаны на связях и отношениях разных понятий. При классификации понятия делятся на сравнимые, между которыми существуют логические связи и отношения, и несравнимые, которые не имеют связей. К несравнимым относятся, например, «машина» и «квадрат», «озеро» и «клетка». У них нет общих элементов и их нельзя сравнивать.

Рисунок 1

Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:

• равнозначные (тождественные);
• перекрещивающиеся;
• подчиняющие и подчинённые.

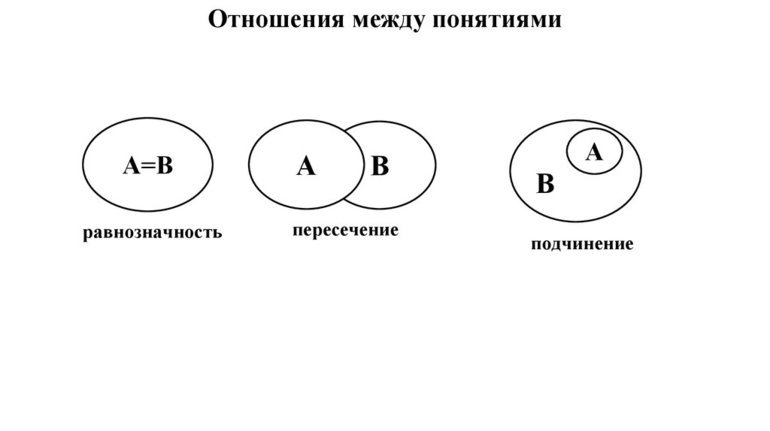
У равнозначных понятий объёмы полностью совпадают. Например, А — писатель Чехов, В — автор пьесы «Вишнёвый сад». Графически тождественность можно представить как два круга, слившиеся в один (Рисунок 1).

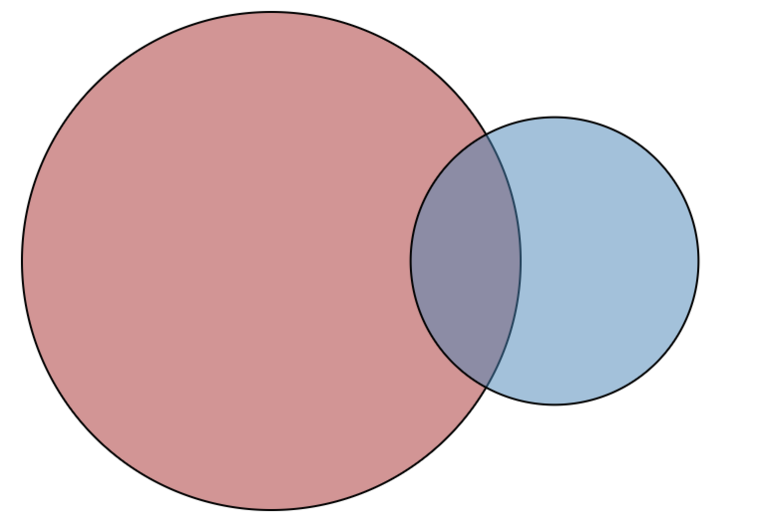
Пересекающимися понятиями, или находящимися в отношении перекрещивания, считаются те, объёмы которых совпадают частично. Пример: A — «математик», B — «репетитор»; A — «студент», B — «спортсмен». Часть объёма понятия «математик» входит в объём понятия «репетитор» и наоборот.

Понятия, состоящие в отношении подчинения, содержат одинаковые элементы, а объём подчинённого целиком входит в объём подчиняющего. Например, «млекопитающее» и «коза».

Несовместимыми называют понятия, не имеющие общих элементов:

• соподчинённые;
• противоположные;
• противоречащие.

Соподчинённые понятия имеют общие элементы и вместе входят в родовое понятие, но в их объёмах общие элементы отсутствуют. Например, А — «корова», B — «овца», C — «млекопитающее». Круги A и B необходимо поместить внутри круга, изображающего объём понятия C, но они не смогут пересекаться, так как не бывает млекопитающих, которые были бы и коровой, и овцой одновременно.

Противоположные понятия — это виды одного и того же рода, но одно из них имеет какой-то признак, а другое не обладает им и содержит признак, несовместимый с первым, направленный против него. Таковы A — «большой дом» и B — «маленький дом». Тут в отличие от отношения противоречия возможны предметы, которые не входят ни в A и ни в B. Если общее родовое C — дом, то в его круге будут изображения двух сегментов A и B, расположенных напротив друг друга, а оставшаяся часть должна соответствовать всем остальным домам (средним, меньше средних).

Противоречащими считается категория понятий, у одного из которых есть какой-то признак, а у другого он отрицается. Например, «чёрный» и «нечёрный», «злой» — «незлой». При этом весь массив родственных элементов делится на две части: одни имеют этот признак, а другие — нет.

Видео:Круги Эйлера, решение задачСкачать

Решение задач, примеры

Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.

Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?

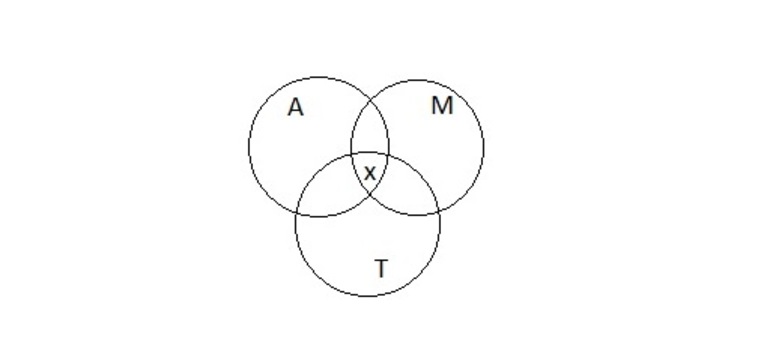
Рисунок 2

Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.

Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…

Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…

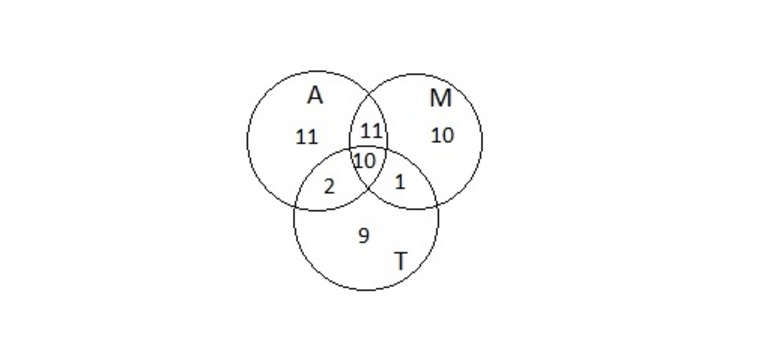
Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).

54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.

Рисунок 3

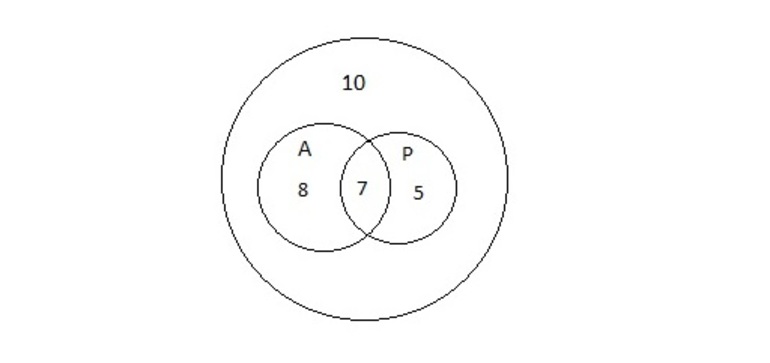
Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?

Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.

Рисунок 4

Круги Эйлера часто применяются для решения самых разных задач. Они служат для развития способности к логическому мышлению у дошкольников. Большой раздел задач для школьников может решаться с помощью диаграмм. Многие учёные в своих исследованиях тоже обращаются к этому методу, который повышает наглядность решаемых проблем и помогает в их обдумывании. Использование простых фигур позволяет свести решение любой сложной задачи к символической логике и упростить ход рассуждений. Диаграммы могут применяться и в обычной жизни, например при поиске работы. Пересечение кругов «лучше всего получается», «больше всего нравится делать» и «чем можно заработать», возможно, даст нужный результат.

🔥 Видео

Решение задач с помощью кругов ЭйлераСкачать

Урок 51. Круги Эйлера. Решение задач с помощью кругов Эйлера (6 класс)Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Множества. Круги Эйлера. Математика 5, 6, 7, 8, 9, 10, 11 класс. Подготовка к ЕГЭ, ОГЭ, ЦТ, экзаменуСкачать

Круги Эйлера в реальной жизни. Математика на QWERTYСкачать

Доказать равенства при помощи диаграмм ВеннаСкачать

Диаграммы Эйлера. Решение заданий №17Скачать

14. Круги ЭйлераСкачать

7 класс. Алгебра. Задача про туристов. Круги Эйлера.Скачать

Круги Эйлера. Логическая задача на множества.Скачать

Доказать равенства при помощи диаграмм Эйлера-Венна. Действия над множествами.Скачать

Операции над множествамиСкачать

Информатика. Круги Эйлера. ОГЭ Задание №8. ЕГЭ задание №17.Скачать

Решение задач с помощью кругов Эйлера. Задача 1Скачать