Функционально-графический метод является, пожалуй, самым красивым и наглядным из всех методов решения уравнений. Это объясняется тем, что он подразумевает использование функций, их свойств и графиков. В этой статье мы дадим краткий обзор трех основных направлений функционально-графического метода:
- Первое направление базируется на использовании графиков функций, отвечающих частям уравнения.
- Второе направление основано на использовании свойств возрастающих и убывающих функций.
- Третье направление функционально-графического метода связано с ограниченностью функций, отвечающим частям уравнения.
Материал этой статьи перекликается с информацией, приведенной в школьных учебниках, например, [1, с. 216-218]. Но здесь мы еще дополним этот материал ссылками на очень подробное описание всех направлений функционально-графического метода, включающее обоснование методов, графические иллюстрации, алгоритмы и решения характерных уравнений.
- Графический метод
- Одна функция убывает, другая — возрастает
- Метод оценки
- Функционально-графический метод решения уравнений и неравенств в школьном курсе алгебры средней школы
- Приложение
- Введение
- 1. Общая теоретическая часть
- 1.3. Метод функциональной подстановки
- Частным случаем функционального метода является метод функциональной подстановки – самый, пожалуй, распространенный метод решения сложных задач математики. Суть метода состоит в введении новой переменной y=ƒ(x), применение которой приводит к более простому выражению. Отдельным случаем функциональной подстановки является тригонометрическая подстановка.
- Тригонометрическое уравнение вида
- log 0, тогда уравнение примет вид t. График параболы у= t при условии t>0 пересекается семейством горизонтальных прямых у=а ровно в двух точках только в области, расположенной под осью t. Искомые значения параметра а=-3, а=-2, а=-1.
- Задания для самостоятельного выполнения:
- 1.
- 2.
- 3.
- 4.
- Задания для самостоятельного выполнения:
- Разработка урока «Функционально-графические методы решения комбинированных уравнений » 11 класс презентация к уроку по алгебре (11 класс) по теме
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
Видео:Занятие 2. Функционально графический методСкачать

Графический метод
Решение уравнений графическим методом предполагает использование графиков функций, отвечающих частям уравнения, для определения количества корней уравнения, их приближенных, а в некоторых случаях и точных значений. Корнями уравнения являются абсциссы точек пересечения графиков соответствующих функций.
Например, графический метод позволяет определить, что уравнение 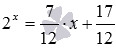
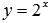

С графическим методом связан ряд нюансов, касающихся сложности построения функций в общем случае, близости графиков на некоторых участках, приблизительности определяемых по графикам результатов и т.д. Все они разобраны в отдельной статье «Графический метод решения уравнений». Там же приведено обоснование метода, алгоритмы и примеры решения характерных уравнений с детальным пояснением хода решения.
Видео:Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Одна функция убывает, другая — возрастает
Идея этого направления функционально-графического метода решения уравнений в следующем: если на некотором числовом промежутке X одна из функций y=f(x) и y=g(x) убывает, а другая – возрастает, то на промежутке X уравнение f(x)=g(x) либо не имеет корней, либо имеет один единственный корень. Этот метод в основном применяется для обоснования вывода об отсутствии корней уравнения, который получен каким-либо методом, например, графическим, или для обоснования единственности корня, который был найден каким-либо способом, часто путем подбора.
Например, при помощи рассматриваемого метода можно решить уравнение 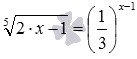


Решение других характерных примеров, обоснование метода, рекомендации по подбору корня и по обоснованию возрастания/убывания функций Вы найдете в этой статье.
Видео:Графический метод решения показательных уравнений и неравенств Алгебра 10 (база)Скачать

Метод оценки
Решение уравнения методом оценки предполагает получение оценок значений выражений, отвечающих частям уравнения, с целью обосновать на их основе отсутствие корней уравнения или перейти к системе более простых уравнений.
Так метод оценки позволяет сделать вывод, что уравнение 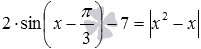


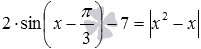
А для уравнения 
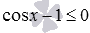



Переход, осуществленный в предыдущем примере, базируется на следующем утверждении:
Уравнение g(x)=h(x) , на ОДЗ для которого значения одного из выражений f(x) и g(x) не больше некоторого числа C , а значения другого – не меньше числа C (пусть g(x)≤C , h(x)≥C ), равносильно системе уравнений 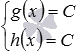
Доказательство этого утверждения, а также доказательства других утверждений, на которых базируется метод оценки, вместе с рекомендациями по получению оценок и решениями характерных примеров, приведены в статье «Метод оценки».
Видео:Решение показательного уравнения функционально-графическим методом. Подготовка к ЕГЭ по математикеСкачать

Функционально-графический метод решения уравнений и неравенств в школьном курсе алгебры средней школы
Муниципальное общеобразовательное учреждение
Юрьевская основная общеобразовательная школа
Муниципальный этап областного методического конкурса
Функционально-графический метод решения уравнений и неравенств в школьном курсе алгебры средней школы.
Анализ школьных учебников
1. Общая теоретическая часть
1.1. Графический метод
1.2. Функциональный метод
1.3. Метод функциональной подстановки
2. Решение уравнений и неравенств с использованием свойств входящих
2.1. Использование ОДЗ
2.2. Использование ограниченности функций
2.3. Использование монотонности функции
2.4. Использование графиков функций
2.5. Использование свойств четности или нечетности и периодичности функций.
3. Решение уравнений и неравенств
3.1. Решение уравнений
3.2. Решение неравенств
Видео:13 Функционально графический способ решенияСкачать

Приложение
Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Введение
Тема моей работы «Функционально-графический метод решения уравнений и неравенств в школьном курсе алгебры средней школы». Одна из главных тем курса алгебры средней школы. Решение уравнений и неравенств играют важную роль в курсе математики средней школы. Школьники начинают знакомиться с неравенствами и уравнениями еще в начальной школе.
Содержание тем «Уравнения» и «Неравенства» постепенно углубляются и расширяются. Так, например, процентное содержание неравенств от всего изучаемого материала в 7 классе составляет 20%, в 8 классе – 25%, в 9 классе – 30%, в 10-11 классах – 35%.
Окончательное изучение неравенств и уравнений происходит в курсе алгебры и начала анализа 10-11 классов. Некоторые ВУЗы включают в экзаменационные билеты уравнения и неравенства, которые часто бывают весьма сложными и требующими разных подходов к решению. В школе один из наиболее трудных разделов школьного курса математики рассматривается только на немногочисленных факультативных занятиях.
В центре внимания этой работы лежит обеспечить более полное раскрытие применения функционально – графического метода к решению уравнений и неравенств в средней школе курса алгебры.
Актуальность данной работы в том, что данная тема входить в ЕГЭ.
Готовя данную работу, я ставила цель, рассмотреть как можно больше типов уравнений и неравенств, решаемых функционально — графическим методом. Также более глубоко изучить данную тему, выявление наиболее рационального решения, быстро приводящего к ответу.
Объект исследования – алгебра 10-11 классов под редакцией и варианты ЕГЭ.
В данной работе рассмотрены часто встречающиеся типы уравнений и неравенств, я надеюсь, что знания, полученные мной в процессе работы, помогут при сдаче школьных экзаменов и при поступлении в ВУЗ. А также может послужить методическим пособием для подготовки школьников к сдаче ЕГЭ.
Анализ школьных учебников
В методической литературе принято все методы, на которых основана школьная линия уравнений и неравенств с 7 по 11 классы, делить на три группы:
üметод разложения на множители;
üметод введения новых переменных;
Рассмотрим третий метод, а именно, использование графиков функций и различных свойств функций.
К применению функционально-графического метода школьников необходимо приучать с самого начала изучения темы «Уравнения».
Решение некоторых задач может быть основано на свойствах монотонности, периодичности, четности или нечетности и т. п. входящих в них функций.
Проанализировав учебники, можно сделать вывод, что данная тема рассматривается только в учебниках математики нового поколения [2], [3], [5], [6] Построение курса в этих учебниках осуществляется на основе приоритетности функционально-графической линии. В остальных учебниках функционально-графический метод решения уравнений и неравенств в отдельную тему не выделен. Использование свойств функции для решения задач упоминается вскользь при изучении других тем. В новых учебниках содержится также достаточное количество заданий этого типа. В учебнике [2] содержатся задания повышенного уровня. Приведена наиболее полная система заданий, систематизированная по каждому свойству функции.
«Алгебра и начала анализа 10-11», учебник для общеоб-разовательных учреждений[5], [6]
, «Алгебра и начала анализа 11», учебник для общеобразовательных учреждений (профильный уровень) [3]
и др. «Алгебра и начала анализа 11», учебник для общеобразовательных учреждений[2]
и др. «Алгебра и начала анализа 11», учебник для общеобразовательных учреждений[4]
и др. «Алгебра и начала анализа 10-11», учебник для общеобразовательных учреждений[1]
Глава 8 «Уравнения и неравенства. Системы уравнений и неравенств» (последняя тема курса)
Глава 6 «Уравнения и неравенства. Системы уравнений и неравенств» (последняя тема курса)
Глава II «Уравнения, неравенства, системы»
Нет отдельно выделенной темы. Но в теме «Решение тригонометрических уравнений и неравенств» формулируется теорема о корне, которая используется в дальнейшем изучении
Нет отдельно выделенной темы
§ §56 Общие методы решения уравнений и неравенств (
§ §27 Общие методы решения уравнений и неравенств (
§ Уравнения (неравенства)вида 
§ §12*Нестадартные методы решения уравнений и неравенств (использование областей существования функций, неотрицательности функций, ограниченности, использование свойств sin и cos, использование производной)
Свойство монотонности функции, четности-нечетности (при выводе формул корней тригонометрических уравнений)
Упоминается свойство монотонности при разборе примера в теме «Показательная функция»
Примеры рассматриваемых уравнений и неравенств
(

Решить уравнение
Сколько корней, принадлежащих данному промежутку, имеет уравнение
Решить уравнение
Анализ ЕГЭ (текстов и результатов)
Единый государственный экзамен как форма аттестации, которая введена в практику российского образования в 2002 году, с 2009 года переходит из экспериментального в штатный режим.
Анализ текстов ЕГЭ показал, что задания, при решении которых используются свойства функций, встречаются каждый год.
В 2003 году в заданиях А9 и С2 при решении можно применить свойства функций:
· А9. Укажите промежуток, которому принадлежат корни уравнения 
· С2. Найдите все значения p, при которых уравнение 
· В 2004 году – задание В2. Сколько корней имеет уравнение 
· В 2005 году задание С2 (решите уравнение 
В 2007 при выполнении задания «Решите уравнение» в части В выпускники при решении уравнения 


Даже хорошо подготовленные учащиеся часто выполняют задания, используя «шаблонные» методы решения, которые приводят к громоздким преобразованиям и вычислениям.
Очевидно, что при выполнении приведенных выше заданий хорошо подготовленный выпускник должен был показать не только знание известных методов решения уравнений или преобразования выражений, но и умение проанализировать условие, соотнести данные и требования задания, вывести из условия различные следствия и т. п., то есть показать определенный уровень развития математического мышления.
Таким образом, при обучении хорошо успевающих учащихся нужно не только позаботиться об усвоении базовой составляющей курса алгебры и начал анализа, (усвоение изученных правил, формул, методов), но и о реализации одной из главных целей обучения математике – развитию мышления учащихся, в частности, математического мышления. Для реализации поставленной цели могут служить элективные курсы.
Действительно, учащиеся общеобразовательных учреждений традиционно знакомятся при изучении математики с графическим методом решения уравнений, неравенств и их систем. Однако в последние годы в содержании обучения математике появляются новые классы уравнений (неравенств) и новые функциональные методы их решения. Тем не менее, содержащиеся в контрольно-измерительных материалах единого государственного экзамена (ЕГЭ) задания (так называемые комбинированные уравнения), решения которых требуют применения только функционально-графического метода, вызывают у учащихся затруднения.
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

1. Общая теоретическая часть
Пусть X и Y — два произвольных численных множества. Элементы этих множеств будем обозначать х и у соответственно и будем называть переменными.
Определение. Числовой функцией, определенной на множестве Х и принимающей значения во множестве Y, называется соответствие (правило, закон), которое каждому х из множества Х сопоставляет одно и только одно значение у из множества Y.
Переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.
Введенное понятие числовой функции является частным случаем общего понятия функции как соответствия между элементами двух или более произвольных множеств.
Пусть Х и Y – два произвольных множества.
Определение. Функцией, определенной на множестве Х и принимающей значения во множестве Y, называется соответствие, соотносящее с каждым элементом множества Х один и только один элемент из множества Y.
Определение. Задать функцию – это значит указать область ее определения и соответствие (правило), при помощи которого по данному значению независимой переменной находятся соответствующие ему значения функции.
С понятием функции связаны два способа решения уравнений: графический и функциональный. Частным случаем функционального метода является метод функциональной, или универсальной подстановки.
Определение. Решить данное уравнение – значит найти множество всех его корней (решений). Множество корней (решений) может быть пустым, конечным или бесконечным. В следующих главах теоретического раздела мы разберем вышеописанные способы решения уравнений, а в разделе «Практикум» покажем их применение в различных ситуациях.
1.1. Графический метод.
На практике для построения графика некоторых функций составляют таблицу значений функции для некоторых значений аргумента, затем наносят соответствующие точки на координатную плоскость и последовательно соединяют их линией. При этом предполагается, что точки достаточно точно показывают ход изменения функции.
Определение. Графиком функции y = f(x) называется множество всех точек
<x, f(x) | x 
Заметим, что, так как функция f сопоставляет каждому x D(f) одно число f(x), то график функции f пересекается любой прямой, параллельной оси ординат, не более, чем в одной точке. И наоборот: всякое непустое множество точек плоскости, имеющее со всякой прямой, параллельной оси ординат, не более одной общей точки, являются графиком некоторой функции. Не всякое множество точек координатной плоскости является графиком какой-либо функции. Например, множество точек окружности не может быть графиком функции, поскольку значению абсциссы внутри окружности, соответствует два значения ординаты.
В общем случае уравнение с одной переменой х можно записать в виде
f(x)=g(x), где f(x) и g(x) – некоторые функции. Функция f(x) является левой частью, а g(x) – правой частью уравнения. Тогда для решения уравнения необходимо построить в одной системе координат графики функций f(x) и g(x). Абсциссы точек пересечения будут являться решениями данного уравнения.
Заметим, что, так как функция f сопоставляет каждому x D(f) одно число f(x), то график функции f пересекается любой прямой, параллельной оси ординат, не более, чем в одной точке. И наоборот: всякое непустое множество точек плоскости, имеющее со всякой прямой, параллельной оси ординат, не более одной общей точки, являются графиком некоторой функции.
Данный метод может использоваться не только для одиночных уравнений, но и для их систем, а также неравенств. В случае с системами необходимо находить не только абсциссы, но и ординаты (если графики функций f(x) и g(x) пересекаются в точке А (х1, у1), то решением системы будет х=х1, у=у1). При решении неравенств ответом будет совокупность абсцисс, при которых график функции f(x) находится выше или ниже (в зависимости от условия) графика функции g(x).
Данное уравнение рационально решать графическим методом.
Точка пересечения графиков имеет координаты (0,5; 0). Следовательно, х=0,5
Данное уравнение рационально решать графоаналитическим методом.
Т. к. 10>1, то данное уравнение равносильно следующему:
Точки пересечения графиков имеют координаты (


Ответ: х=
1.2. Функциональный метод
Не всякое уравнение вида f(x)=g(x) в результате преобразований может быть приведено к уравнению того или иного стандартного вида, для которого подходят обычные методы решения. В таких случаях имеет смысл использовать такие свойства функций f(x) и g(x) как монотонность, ограниченность, четность, периодичность и др. Так, если одна из функций возрастает, а другая убывает на определенном промежутке, то уравнение f(x) = g(x) не может иметь более одного корня, который, в принципе, можно найти подбором. Далее, если функция f(x) ограничена сверху, а функция g(x) – снизу так, что f(x)мах=А g(x)мin=A, то уравнение f(x)=g(x) равносильно системе уравнений
Также при использовании функционального метода рационально использовать некоторые теоремы, приведенные ниже. Для их доказательства и использования необходимы следующие уравнения общего вида:

Теорема 1. Корни уравнения (1) являются корнями уравнения (2).
Теорема 2. Если f(x) – возрастающая функция на интервале a


Данное уравнение рационально решать функциональным методом.

Видео:8 класс, 21 урок, Графическое решение уравненийСкачать

1.3. Метод функциональной подстановки
Видео:Урок по теме ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ 7 КЛАСССкачать

Частным случаем функционального метода является метод функциональной подстановки – самый, пожалуй, распространенный метод решения сложных задач математики. Суть метода состоит в введении новой переменной y=ƒ(x), применение которой приводит к более простому выражению. Отдельным случаем функциональной подстановки является тригонометрическая подстановка.
Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Тригонометрическое уравнение вида
где R – рациональная функция, k,n,m,lÎZ, с помощью тригонометрических формул двойного и тройного аргумента, а также формул сложения можно свести к рациональному уравнению относительно аргументов sinx, cosx, tgx, ctgx, после чего уравнение (3) может быть сведено к рациональному уравнению относительно t=tg(x/2) c помощью формул универсальной тригонометрической подстановки




Следует отметить, что применение формул (4) может приводить к сужению ОДЗ исходного уравнения, поскольку tg(x/2) не определен в точках x=π+2πk, kÎZ, поэтому в таких случаях нужно проверять, являются ли углы x=π+2πk, kÎZ корнями исходного уравнения.

 |
Данное уравнение рационально решать методом функциональной подстановки.
Пусть u = sinx и v = + 
В таком случае из уравнения получаем систему уравнений
 |
Пусть теперь r = u+v и s=uv, тогда из системы уравнений следует
 |
Отсюда с учетом того, что r≥0, получаем r = 2 и s = 1. Следовательно, имеет место
 |
Поскольку, u = sinx и u = 1, то sinx = 1 и x = π/2+2πk, kÎZ
Ответ: x = π/2+2πk, kÎZ

Данное уравнении рационально решать методом функциональной подстановки.
Так как tgx не определен при x = π/2+πk, kÎZ, а sinx+tgx=0 при x = πk, kÎZ, то углы x = πk/2, kÎZ не входят в ОДЗ уравнения.
Используем формулы тангенса половинного угла и обозначим t=tg(x/2), при этом по условию задачи t≠0;±1, тогда получим






Так как t≠0;±1, то данное уравнение равносильно уравнению

откуда t = ± 

Ответ: x = ±2arctg 
Данное уравнение рационально решать методом функциональной подстановки.
Так как tgx+ctgx=2, то tgx+1/ tgx=2. Отсюда следует, что tgx=1 и x = π/4+πk, kÎZ
2. Решение уравнений и неравенств с использованием свойств входящих в них функций
Иногда знание ОДЗ позволяет доказать, что уравнение (или неравенство) не имеет решений, а иногда позволяет найти решения уравнения (или неравенства) непосредственной подстановкой чисел из ОДЗ.
Пример 1. Решить уравнение
Решение. ОДЗ этого уравнения состоит из всех х, одновременно удовлетворяющих условиям 3-х
Ответ: решений нет.
Пример 2. Решить уравнение

Решение. ОДЗ этого уравнения состоит из всех х, одновременно удовлетворяющих условиям 


Ответ:
Пример 3. Решить неравенство

Решение. ОДЗ неравенства (2) состоит из всех х, одновременно удовлетворяющих условиям 







Пример 4. Решить неравенство

Решение. ОДЗ неравенства (3) есть все х, удовлетворяющие условию 0 A и g(x)
Заметим, что роль числа А часто играет нуль, в этом случае говорят о сохранении знака функций f(x) и g(x) на множестве М.
Пример 1. Решить уравнение
Решение. Для любого действительного числа х имеем 

Ответ: нет решений.
Пример 2. Решить уравнение

Решение. Очевидно, что х=0, х=1, х=-1 являются решениями уравнения (9). Для нахождения других решений уравнения (9) в силу нечетности функции 



Разобьем множество х>0, 
Перепишем уравнение (9) в виде 



Пусть х принадлежит промежутку (1;+∞). Для каждого из таких значений х функция 


Если же х>2 , то 
Итак, х=0,х=1 и х=-1 и только они являются решениями исходного уравнения.
Ответ:
Пример 3. Решить неравенство

Решение. ОДЗ неравенства (10) есть все действительные х, кроме х=-1. Разобьем ОДЗ на три множества: -∞ 0 функция 


Пример 2. Решить неравенство

Решение. Каждая из функций 







Функция 















Ответ: единственный корень.
2. 4. Использование графиков функций.
При решении уравнений и неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей в одной и той же системе координат. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение уравнения (или неравенства) было очевидно.
Обратим внимание, что эскиз графика лишь помогает найти решение, но писать, что из графика следует ответ, нельзя, ответ еще надо обосновать.
Пример 1. Решить неравенство

Решение. Область допустимых значений неравенства (26) есть все х из промежутка [-1;1]. Эскизы графиков функций 

Докажем это. Для каждого 




Ответ: 
Пример 2. Решить уравнение

Решение. ОДЗ уравнения (27) есть все х из промежутка 





Ответ: решений нет.
Пример 3. Решить уравнение

Решение. Эскизы графиков функций 

Для этого докажем, что х из промежутка (-1; +∞) справедливы неравенства 





Следовательно, требуемое утверждение доказано, и уравнение (28) имеет единственный корень х=-1.
Пример 4. Решить неравенство

Решение. Область допустимых значений данного неравенства состоит из всех х, удовлетворяющих условиям х>-2, 





Эскизы графиков функций 




Поэтому неравенство (31) не имеет решений, а неравенство (30) будет иметь решениями все х из промежутка 
А) Пусть 


Следовательно, неравенство (30), а вместе с ним и исходное неравенство (29) не имеют решений на интервале 
Б) Пусть 


Следовательно, любое такое х является решением неравенства (30), а поэтому и исходного неравенства (29).
В) Пусть х>0. На этом множестве исходное неравенство равносильно неравенству (31). Очевидно, что для любого х из этого множества справедливы неравенства


1) неравенство (31) не имеет решений на том множестве, где 

2) неравенство (31) не имеет решений на том множестве, где 

Если функция F(x) – периодическая, то решение уравнения F(x)=0 или неравенства F(x)>0 (F(x) 
Видео:Графический метод решения уравнений 8 классСкачать

Видео:Графический способ решения уравнений 1Скачать

Видео:Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Видео:Графический способ решения уравнений и неравенств | Алгебра 10 классСкачать

log  0, тогда уравнение примет вид t
0, тогда уравнение примет вид t . График параболы у= t
. График параболы у= t  при условии t>0 пересекается семейством горизонтальных прямых у=а ровно в двух точках только в области, расположенной под осью t. Искомые значения параметра а=-3, а=-2, а=-1.
при условии t>0 пересекается семейством горизонтальных прямых у=а ровно в двух точках только в области, расположенной под осью t. Искомые значения параметра а=-3, а=-2, а=-1.
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Задания для самостоятельного выполнения:
Видео:Алгебра 9 класс. Графическое решение систем уравненийСкачать

1. 
Видео:Решение системы линейных уравнений графическим способом. 7 классСкачать

2. 
Видео:Решение системы уравнений графическим методомСкачать

3. 
Видео:РЕШЕНИЕ ПОКАЗАТЕЛЬНОГО УРАВНЕНИЯ ФУНКЦИОНАЛЬНО ГРАФИЧЕСКИМ МЕТОДОМСкачать

4. 
5.
6.
7.
8.
1.
Область допустимых значений уравнения: R
f(x)=
g(x)=
Область значений f(x) = [0; +∞), область значений g(x) = [-1;0].
Данное уравнение равносильно системе:
2.
Область допустимых значений уравнения: R
f(x)=
g(x)=
Область значений f(x) = [0; +∞), область значений g(x) = [-1;0].
Данное уравнение равносильно системе:


Видео:Графический метод решения систем линейных уравнений 7 классСкачать

Задания для самостоятельного выполнения:
1.
2.
3.
4.
1. Единый государственный экзамен: математика: контрольные измерительные материалы: .- Москва: Просвещение; Санкт-Петербург: Просвещение, 20с.
2. , , «Уравнения и неравенства. Нестандартные методы решения». Москва: Дрофа, с.
3. Стойлова . Москва – 2002г.
4. Федеральный банк экзаменационных материалов. ЕГЭ 2008 Математика. Сборник экзаменационных заданий. , , Сергеев : Эксмо, с.
5. Самое полное издание реальных заданий ЕГЭ 2008 Математика: , , и другие – Москва: АСТ: Астрель, с.
6. , Прокофьев решения неравенств с одной переменной.
7. Алгебра учебник для 7 класса общеобразовательных учреждений. , Миндюк редакцией . – 11-е издание – Москва: Просвещение, 2002.-223с.
8. Алгебра учебник для 8 класса общеобразовательных учреждений. , Миндюк редакцией . – 9-е издание – Москва: Просвещение, 2001.-240с.
9. Алгебра учебник для 9 класса общеобразовательных учреждений. , Миндюк редакцией . – 4-е издание – Москва: Просвещение, 1997.-272с.
10. Алгебра и начала анализа 10-11 классы. Задачник для общеобразовательных учреждений под редакцией . – 5-е издание-Москва: Мнемозина, 2004. – 315с.
11. Издательский дом «Первое сентября» Математика. Научно-методическая газета №10-2006.
12. Издательский дом «Первое сентября» Математика. Научно-методическая газета №8-2007.
13. Издательский дом «Первое сентября» Математика. Научно-методическая газета №16 – 2007.
15. http://mmmf. *****/zaoch/math/ur_i_ner. pdf
Область применения свойств функции при решении неравенств очень широка. Наличие свойств (ограниченность, монотонность и т. д.) функций, входящих в неравенства позволяет применить нестандартные методы решения к стандартным по формулировке задачам – неравенствам. Пример, связанный с композицией функций.
Пример (использование области определения функции)

Разработка урока «Функционально-графические методы решения комбинированных уравнений » 11 класс
презентация к уроку по алгебре (11 класс) по теме
Материал содержит разработку урока по теме «Функционально-графические методы решения комбинированных уравнений » для 11 класса по учебнику А.Г.Мордковича
Скачать:
| Вложение | Размер |
|---|---|
| urok_funktsionalno-graficheskie_sposoby_resheniya_uravneniy.ppt | 795 КБ |
Предварительный просмотр:
Подписи к слайдам:
Урок в 11 классе «Функционально-графические методы решения комбинированных уравнений » Тип урока- урок комплексного применения знаний и способов действий. Оборудование — проектор, экран, презентация для сопровождения урока. Учебно-методическое обеспечение — Алгебра и начала анализа 11 класс. В 2 ч. Учебник для общеобразовательных учреждений (профильный уровень)/А.Г.Мордкович, П.В. Семенов.-4-е изд., доп.- М.:Мнемозина,2007. Метод решения хорош, если с самого начала мы можем предвидеть – и в последствии подтвердить это, — что, следуя этому методу, мы достигнем цели . Г. Лейбниц Лапкина О.А. МБОУ СОШ №22 г.Нижний Новгород
Цели урока: Образовательные — обобщить и закрепить навыки применения свойств функций при решении уравнений, систематизировать знания учащихся по теме «Уравнения», создать содержательные и организационные условия для применения учащимися комплекса знаний и способов действий при решении нестандартных уравнений. Развивающие — развивать логическое мышление, навыки исследовательской деятельности ( планирование своей работы, выдвижение гипотез, анализ и обобщение полученных результатов), интерес и инициативу учащихся, повышать их математическую культуру; в процессе повторения ученики должны перейти от одного уровня математической деятельности к следующему, более высокому, сделав для себя открытия в этой теме. Воспитательные — развивать у учащихся трудолюбие, упорство в достижении поставленной цели, способствовать развитию творческой деятельности учащихся, потребности к самообразованию, помогать учащимся осуществлять самооценку своего труда.
Ход урока № Структурные элементы Время Деятельность учащихся 1 Организационный момент. 1 мин. Обсуждение 2 Проверка опорных моментов домашнего задания и постановка проблемы: -акцентирование теории по теме, -применение теории на практике, -выдвигаемая гипотеза. 3 мин 5 мин. 1 мин. Отвечают устно, проводят обсуждение ответов, самооценка. Выдвигают свои идеи по дальнейшему ходу действий 3 Первичный анализ наблюдений. 5 мин. Предлагают способы решения уравнения, анализируют ход решения и методы решения. 4 Исследование новых видов уравнений. Проверка усвоения изученных методов(самостоятельная работа) 12мин. 15мин. Учащиеся работают самостоятельно, при необходимости получают консультацию учителя, проверяя свои действия с помощью слайдов. Результаты проверочной работы выводятся на экран. Самооценка. 5 Подведение итогов. 2мин. Заполняют таблицы, подводят итог урока. 6 Домашнее задание. 1 мин. Записывают домашнее задание.
y x 1 -1 Найдите множество значений функции Ответ: Е(у): [ -2,5 ; 0, 5 ] . у= sin x у=1,5 sin x — 1 у= 1,5 sin x — 1 0
Метод оценки Найдите наибольшее целое значение функции Ответ: у=3.
Общие методы решения уравнений Функционально-графические По графику По свойствам Переход к равносильным уравнениям Метод разложения на множители Метод введения новой переменной Аналитические
Построение графиков функций левой и правой частей уравнения (решением являются абсциссы точек (точки) пересечения графиков) Функционально – графические методы Использование свойств функций левой и правой частей уравнения (монотонность, четность, нечетность) Использование ограниченности функций левой и правой частей уравнения (метод оценки)
y x x= 0 О 1 Графический способ решения уравнений
Оценка левой и правой частей уравнения log 2 (2x-x²+15) = x²-2x+5 1)2x-x²+15= -((x²-2x+1)-1- 1 5) = -(x-1)²+16 ≤ 16 Если 0 Мне нравится
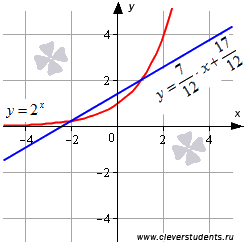

























 0, тогда уравнение примет вид t
0, тогда уравнение примет вид t . График параболы у= t
. График параболы у= t  при условии t>0 пересекается семейством горизонтальных прямых у=а ровно в двух точках только в области, расположенной под осью t. Искомые значения параметра а=-3, а=-2, а=-1.
при условии t>0 пересекается семейством горизонтальных прямых у=а ровно в двух точках только в области, расположенной под осью t. Искомые значения параметра а=-3, а=-2, а=-1.
























