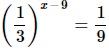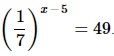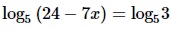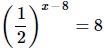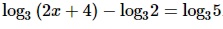Решение уравнений егэ база примеры

Видео:Решаем ВСЕ уравнения из сборника Ященко | Parta 2023 | Базовая математикаСкачать

Уравнения. Базовый уровень

Автор: Толмачева Надежда Алексеевна.

Видео:ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать

Стереометрия на ЕГЭ

Цикл уроков для подготовки к заданию 13 профильного ЕГЭ по математике.

Видео:ЕГЭ База: задание 17 | ЕГЭ просто | Простейшие уравненияСкачать

Экспресс-курсы по подготовке к ЕГЭ

Пущинский государственный естественно-научный институт проводит бесплатные экспресс-курсы с 1 марта по 25 апреля 2022 года для выпускников 11 классов.

Видео:Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Словарь архаизмов и историзмов по пьесам М.Горького

Пьесы: «Мещане», «На дне», «Враги», «Егор Булычов и другие».

Видео:ВСЕ виды уравнений. Задание 5Скачать

Задание №7 ЕГЭ по математике базового уровня

Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Простейшие уравнения

В задании №7 базового уровня ЕГЭ по математике необходимо решить

Простейшие (Protozoa) — тип одноклеточных животных.

Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня

Вариант 7МБ1

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 3) 2 = x 2 + 2 · x · 3 + 3 2 = x 2 + 6x + 9

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 9) 2 = x 2 – 2 · x · 9 + 9 2 = x 2 – 18x + 81

После преобразования выражение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x 2 + 6x + 9 = x 2 – 18x + 81

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую. При переносе из одной части равенства в другую знак меняется на противоположный.

x 2 + 6x – x 2 + 18x = 81 – 9

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x 2 и x.

x 2 + 6x – x 2 + 18x = (x 2 – x 2 ) + (6x +18x) = 0 + 24x = 24x

Выражение примет вид:

Преобразуем правую часть. 81 – 9 = 72

Выражение примет вид:

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

Решение в общем виде:

Вариант 7МБ2

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 2) 2 = x 2 + 2 · x · 2 + 2 2 = x 2 + 4x + 4

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 8) 2 = x 2 – 2 · x · 8 + 8 2 = x 2 – 16x + 64

После преобразования выражение примет вид:

x 2 + 4x + 4 = x 2 – 16x + 64

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую. При переносе из одной части равенства в другую знак меняется на противоположный.

x 2 + 4x – x 2 + 16x = 64 – 4

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x 2 и x.

x 2 + 4x – x 2 + 16x = (x 2 – x 2 ) + (4x +16x) = 0 + 20x = 20x

Выражение примет вид:

Преобразуем правую часть. 64 – 4 = 60

Выражение примет вид:

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

Решение в общем виде:

Вариант 7МБ3

Алгоритм выполнения

1. Перенести вычитаемое в правую сторону равенства с противоположным знаком.
2. Преобразовать правую часть с учетом свойства: log_ax + log_ay = log_a (x · y).
3. Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
4. Решить уравнение относительно x.

Решение:

Вариант 7МБ4

Найдите корень уравнения 3 x− 3 = 81.

Алгоритм выполнения

1. Привести выражения в степенях к одинаковому основанию. В данном случае – это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.
2. Когда основания равны, можно приравнять значения степеней

Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором – 9, при третьем – три.

Значит, 81 это три в четвертой степени. Запишем это:

Решение:

Ответ: 7

Вариант 7МБ5

Найдите корень уравнения log₂( x − 3) = 6 .

Алгоритм выполнения

1. Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.

Решение:

Вариант 7МБ6

Найдите отрицательный корень уравнения x 2 − x − 6 = 0.

Алгоритм выполнения

1. Вычислить дискриминант
2. Найти корни
3. Выбрать необходимый корень

Решение:

D = -(1) 2 − 4 • 1 • (-6) = 25

Так как нам необходим отрицательный корень – ответ -2

Вариант 7МБ7

Решите уравнение х 2 = –2х + 24.

Если уравнение имеет больше одного

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Алгоритм выполнения

1. Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
2. Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
3. Записываем в качестве ответа большее из полученных 2 чисел.

Решение:

Поскольку требуется указать больший из корней, то ответом будет 4.

Вариант 7МБ8

Найдите корни уравнения 4 х–6 = 64.

Алгоритм выполнения

1. Представляем 64 как степень с основанием 4, т.е. приводим выражения справа и слева к степеням с одинаковым основанием.
2. Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
3. Находим корень ур-ния.

Решение:

Вариант 7МБ9

Найдите корень уравнения log₃ (2x – 5) = 2.

Алгоритм выполнения

1. Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов log_xx=1 и log_xy n =nlog_xy.
2. Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
3. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ10

Найдите корень уравнения

Алгоритм выполнения

1. Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а) х =а –х .
2. Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
3. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ11

Найдите корень уравнения (х – 8) 2 = (х – 2) 2 .

Алгоритм выполнения

1. Раскрываем скобки слева и справа, используя ф-

Луб — это сложная проводящая ткань, по которой продукты фотосинтеза (органические вещества) транспортируются из листьев ко всем органам растения (к корневищам, плодам, семенам и т. д.).

Решение:

х 2 – 2 · х ·8 + 8 2 = х 2 – 2 · х · 2 + 2 2

Вариант 7МБ12

Найдите корень уравнения

Алгоритм выполнения

1. Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а) х =а –х .
2. Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
3. Решаем его.

Решение:

Вариант 7МБ13

Решите уравнение х 2 – 25 = 0

Алгоритм выполнения

1. Переносим 25 в правую часть ур-ния.
2. Выражаем из ур-ния х путем извлечения корня из 25.
3. Определяем корни, сравниваем их, определяем больший.

Решение:

Для ответа берем 5.

Вариант 7МБ14

Найдите корень уравнения

Алгоритм выполнения

1. Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
2. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ15

Найдите корень уравнения

Алгоритм выполнения

1. Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а) х =а –х .
2. Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
3. Решаем его.

Решение:

Вариант 7МБ16

Найдите корень уравнения

Видео:ЛОГАРИФМЫ с нуля за 25 минут | ЕГЭ Математика | Аня Матеманя | ТопскулСкачать

Репетитор по математике

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Стоимость занятий

Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Видео:Решение варианта №13 Ященко по профильной математике 2024 | Подготовка к ЕГЭ с нуляСкачать

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Видео:Простейшие уравнения ЕГЭ 2024/ Все типы задания №17 ЕГЭ БАЗАСкачать

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

🔍 Видео

Как решить ЕГЭ по математике (база): 7, 16, 17 задания | Решу ЕГЭ за 10 минутСкачать

ВСЕ ТИПЫ заданий №16 на ЕГЭ | Базовая математика ЕГЭ 2023 | УмскулСкачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Решение логарифмических уравнений #shortsСкачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать