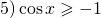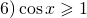- Арккосинус. Решение уравнения cos x=a
- п.1. Понятие арккосинуса
- п.2. График и свойства функции y=arccosx
- п.3. Уравнение cosx=a
- п.4. Формула арккосинуса отрицательного аргумента
- п.5. Примеры
- Узнать ещё
- a»>cosx>a
- Тригонометрические уравнения. Как решать тригонометрические уравнения?
- Тригонометрические уравнения – уравнения, содержащие переменную под знаком тригонометрических функций.
- Как решать тригонометрические уравнения:
- 🔥 Видео
Видео:КАК РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ? // УРАВНЕНИЕ COSX=AСкачать
Арккосинус. Решение уравнения cos x=a
п.1. Понятие арккосинуса
В записи (y=cosx) аргумент x — это значение угла (в градусах или радианах), функция y – косинус угла, действительное число в пределах [-1;1]. Т.е., по заданному углу мы находим косинус.
Можно поставить обратную задачу: по заданному косинусу найти угол. Но одному значению косинуса соответствует бесконечное количество углов. Например, если (cosx=1), то (x=2pi k, kinmathbb); (cosx=0), то (x=fracpi2+pi k, kinmathbb) и т.д.
Поэтому, чтобы построить однозначную обратную функцию, ограничим значения углов x отрезком, на котором косинус принимает все значения из [-1;1], но только один раз: (0leq xleq pi) (верхняя половина числовой окружности).
(arccosfrac12=fracpi3, arccosleft(-frac<sqrt>right)=frac)
(arccos2) – не существует, т.к. 2> 1
п.2. График и свойства функции y=arccosx
1. Область определения (-1leq xleq1) .
2. Функция ограничена сверху и снизу (0leq arccosxleq pi) . Область значений (yin[0;pi])
3. Максимальное значение (y_=pi) достигается в точке x =-1
Минимальное значение (y_=0) достигается в точке x =1
4. Функция убывает на области определения.
5. Функция непрерывна на области определения.
п.3. Уравнение cosx=a
 | Значениями арккосинуса могут быть только углы от 0 до π (180°). А как выразить другие углы через арккосинус? |
Углы в нижней части числовой окружности записывают через отрицательный арккосинус. А углы, которые превышают π по модулю, записывают через сумму арккосинуса и величины, которая ‘не помещается» в область значений арккосинуса.
1) Решим уравнение (cosx=frac12).
Найдем точку (frac12) в числовой окружности на оси косинусов (ось OX). Построим вертикаль – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках, соответствующих углам (pmfracpi3) — это базовые корни.
Если взять верхний корень (fracpi3) и прибавить к нему полный оборот (fracpi3+2pi=frac), косинус полученного угла (cosfrac=frac12), т.е. (frac) также является корнем уравнения. Корнями будут и все другие углы вида (fracpi3+2pi k) (с любым количеством добавленных или вычтенных полных оборотов). Аналогично, корнями будут все углы вида (-fracpi3+2pi k).
Получаем ответ: (x=pmfracpi3+2pi k)
Заметим, что полученный ответ является записью вида
(x=pm arccosfrac12+2pi k)
А т.к. арккосинус для (frac12) точно известен и равен (fracpi3), то мы его и пишем в ответе.
Но так бывает далеко не всегда.
2) Решим уравнение (cosx=0,8)
 | Найдем точку 0,8 в числовой окружности на оси косинусов (ось OX). Построим вертикаль – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках. По определению верхняя точка – это угол, равный arccos0,8. Тогда нижняя точка – это тот же угол, но отложенный в отрицательном направлении обхода числовой окружности, т.е. (–arccos0,8). Добавление или вычитание полных оборотов к каждому из решений даст другие корни. Получаем ответ: (x=pm arccos0,8+2pi k) |
п.4. Формула арккосинуса отрицательного аргумента
Докажем полезную на практике формулу для (arccos(-a)).
 | По построению: $$ begin angle DA’O=angle BAO=angle CAO=90^\ OD=OB=OC=1\ OA’=OA=a end Rightarrow $$ (по катету и гипотенузе) begin Delta DA’O=Delta BAO=Delta CAORightarrow\ Rightarrow angle DOC=angle A’OA-alpha+alpha=angle A’OA=180^=pi\ -arccosa+pi=arccos(-a) end |
п.5. Примеры
Пример 1. Найдите функцию, обратную арккосинусу. Постройте графики арккосинуса и найденной функции в одной системе координат.
Для (y=arccosx) область определения (-1leq xleq 1), область значений (0leq yleq pi).
Обратная функция (y=cosx) должна иметь ограниченную область определения (0leq xleq pi) и область значений (-1leq yleq 1).
Строим графики:
Графики симметричны относительно прямой y=x.
Обратная функция найдена верно.
Пример 2. Решите уравнения:
a) (cos x=-1) (x=pi+2pi k) | б) (cos x=frac<sqrt>) (x=pmfracpi4+2pi k) |
в) (cos x=0) (x=pmfracpi2+2pi k=fracpi2+pi k) | г) (cos x=sqrt) (sqrtgt 1, xinvarnothing) Решений нет |
д) (cos x=0,7) (x=pm arccos(0,7)+2pi k) | e) (cos x=-0,2) (x=pm arccos(-0,2)+2pi k) |
Пример 3. Запишите в порядке возрастания: $$ arccos0,8; arccos(-0,5); arccosfracpi7 $$
 | Способ 1. Решение с помощью числовой окружности |
Отмечаем на оси косинусов (ось OX) точки с абсциссами 0,8; -0,5; (fracpi7approx 0,45)
Значения арккосинусов (углы) считываются на верхней половине окружности: чем меньше косинус (от 1 до -1), тем больше угол (от 0 до π).
Получаем: (angle A_1OAltangle A_2OAangle A_3OA)
$$ arccos0,8lt arccosfracpi7lt arccos(-0,5) $$
Отмечаем на оси OX аргументы 0,8; -0,5; (fracpi7approx 0,45). Восстанавливаем перпендикуляры на кривую, отмечаем точки пересечения. Из точек пересечения с кривой восстанавливаем перпендикуляры на ось OY — получаем значения арккосинусов по возрастанию: $$ arccos0,8lt arccosfracpi7lt arccos(-0,5) $$
Арккосинус – функция убывающая: чем больше аргумент, тем меньше функция.
Поэтому располагаем данные в условии аргументы по убыванию: 0,8; (fracpi7); -0,5.
И записываем арккосинусы по возрастанию: (arccos0,8lt arccosfracpi7lt arccos(-0,5))
Пример 4*. Решите уравнения:
(a) arccos(x^2-3x+3)=0) begin x^2-3x+3=cos0=1\ x^2-3x+2=0\ (x-2)(x-1)=0\ x_1=1, x_2=2 end Ответ:
(б) arccos^2x-arccosx-6=0)
( text -1leq xleq 1 )
Замена переменных: (t=arccos x, 0leq tleq pi)
Решаем квадратное уравнение: $$ t^2-t-6=0Rightarrow (t-3)(t+2)=0Rightarrow left[ begin t_1=3\ t_2=-2lt 0 — text end right. $$ Возвращаемся к исходной переменной: begin arccosx=3\ x=cos3 end Ответ: cos3
(в) arccos^2x-pi arccosx+frac=0)
( text -1leq xleq 1 )
Замена переменных: (t=arccos x, 0leq tleq pi)
Решаем квадратное уравнение: begin t^2-pi t+frac=0\ D=(pi^2)-4cdot frac=frac, sqrt=fracpi3\ left[ begin t_1=frac=fracpi3\ t_2=frac=frac end right. Rightarrow left[ begin arccosx_1=fracpi3\ arccosx_2=frac end right. Rightarrow left[ begin x_1=cosleft(fracpi3right)=frac12\ x_2=cosleft(fracright)=-frac12 end right. end Ответ: (left)
Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать
Узнать ещё
Знание — сила. Познавательная информация
Видео:Алгебра 10 класс (Урок№41 - Уравнение cos x = a.)Скачать
a»>cosx>a
Рассмотрим решение тригонометрических неравенств вида cosx>a на единичной окружности.
Косинус — это абсцисса точки. Значит, cosx=a в точках пересечения единичной окружности и прямой x=a (прямая, параллельная оси oy), cosx>a справа от этой прямой, cosxa, нам нужна часть окружности, расположенная правее прямой y=a. Соответственно, от взаимного расположения окружности и этой прямой зависит решение неравенства cosx>a.
1) cosx>a при 0
На единичной окружности отмечает точки пересечения ее с прямой y=a. Первая точка — arccos a. Чтобы найти вторую, рассуждаем так: решения неравенства cosx>a лежат справа от этой прямой (заштриховываем соответствующую дугу окружности). Поэтому, чтобы попасть из 1й точки во вторую, идем по часовой стрелке. При таком обходе угол уменьшается. Доходим до нуля, дальше — отрицательные углы. Вторую точку отделяет от нуля такой же угол, что и первую. Но поскольку мы шли по часовой стрелке, ее берем со знаком минус.
Интервал записываем по возрастанию, поэтому сначала идет -arccos a, потом уже arccos a. С учетом периодичности синуса, к каждому из концов интервала прибавляем 2пn, где n — целое число (n принадлежит Z). Если неравенство нестрогое, точки закрашиваем и включаем в ответ (с квадратными скобками).
2) cosx>-a при 0
Рассуждения аналогичны предыдущему случаю. Отличие — нужно искать arccos(-a) (чуть позже я расскажу, как легко запомнить арккосинусы отрицательных чисел).
3) cosx>0
4) cosx>-1
За исключением одной точки,вся окружность лежит правее прямой y=a. Чтобы записать ответ в виде интервала, первой точкой берем -п. Поскольку во 2ю попадаем через полный оборот окружности, то есть через 2п, то -п +2п=п. К обоим концам интервала прибавляем 2пn.
В этом случае точки исключать не нужно, x — любое число: (-∞;+∞).
Единственной точкой, удовлетворяющей данному условию, является 0. С учетом периодичности косинуса, решение — множество точек x=2пn.
7) cosx>a при a>1
Единичная окружность полностью лежит слева от прямой y=a, поэтому при таких a нет ни одной точки, удовлетворяющей условию cosx>a. Значит, решений нет.
8) cosx>-a при a>1
Единичная окружность целиком лежит правее прямой y=a, поэтому x — любое число: (-∞;+∞).
И в заключении — конкретный пример решения неравенства вида cosx>a:
Видео:Тригонометрические уравнения с помощью окружности. cosx=aСкачать
Тригонометрические уравнения. Как решать тригонометрические уравнения?
Тригонометрические уравнения – уравнения, содержащие переменную под знаком тригонометрических функций.
Если проще: это уравнения, в которых неизвестные (иксы) или выражения с ними находятся внутри синусов , косинусов , тангенсов и котангенсов .
Видео:Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать
Как решать тригонометрические уравнения:
Любое тригонометрическое уравнение нужно стремиться свести к одному из видов:
где (t) – выражение с иксом, (a) – число. Такие тригонометрические уравнения называются простейшими. Их легко решать с помощью числовой окружности ( тригонометрического круга ) или специальных формул:
(sin x=a) (⇔) ( left[ beginx=arcsin a+2πn, n∈Z\ x=π-arcsin a+2πl, l∈Zendright.)
если (a∈[-1;1])
Инфографику о решении простейших тригонометрических уравнений смотри здесь: (sinx=a) , (cosx=a) , (tgx=a) и (ctgx=a) .
Пример. Решите тригонометрическое уравнение (sinx=-)(frac).
Решение:
Ответ: (x=) (frac) (+πk), (k∈Z).
Пример. Решите тригонометрическое уравнение (cos(3x+frac)=0).
Решение:
Ответ: (x=) (frac) (+) (frac) (x=-) (frac) (+) (frac) , (k∈Z).
Сводить тригонометрические уравнения к простейшим – задача творческая, тут нужно использовать и тригонометрические формулы , и особые методы решений уравнений:
— Метод введения новой переменной (самый популярный в ЕГЭ).
— Метод разложения на множители .
— Метод вспомогательных аргументов.
Рассмотрим пример решения квадратно-тригонометрического уравнения
Пример. Решите тригонометрическое уравнение (2cos^2x-5cosx+2=0)
Решение:
 |
Ответ: (x=±) (frac) (+2πk), (k∈Z).
Пример решения тригонометрического уравнения с исследованием ОДЗ:
Пример(ЕГЭ). Решите тригонометрическое уравнение (frac<2cos^2x-sin>) (=0)
